各向异性地基中盾构隧道开挖面稳定性分析

刘文洁，王同华，肖建勋

(1.南京科技职业学院，江苏 南京 210048；2.北京城建设计发展集团股份有限公司，浙江 杭州 310000； 3.江苏省地质工程有限公司，江苏 南京 210018)

0 引 言

目前我国正在大力发展城市轨道交通建设中，现已有27 个城市共计112 条城市轨道交通线路投入运营，此外，仍有不少城市及不少新的轨道交通线路正在积极筹划及建设中。在城市轨道交通建设中，常采用盾构法进行车站区间的施工，施工中若施加在开挖面上的支护压力过小会导致土体坍塌，施加过大则会导致土体隆起，相应的开挖面失稳事故[1]屡见报道，因此在施工过程中施加合理的支护压力是确保开挖面稳定性的关键。

针对开挖面极限支护压力方面，不少学者已进行相应的理论[2-12]及试验研究[13-15]。G. ANAGNOSTOU等[2]建立了经典的“楔形体-棱柱体”模型，并得到相应的极限平衡解。秦建设[3]、魏纲等[4]、G.ANAGNOSTOU[5]及R.P.CHEN等[6]对该模型进行一定的改进，并做了进一步的解析研究；E.LECA等[7]提出3种由1个或2个圆锥体构成的机动场；G. MOLLON等[8]构造三维平动多块体集机动场；吕玺琳等[9]则参照Terzaghi地基承载力的计算方法提出破坏模式，并各自在相应的破坏模式基础上得到相应的上(下)限解；试验研究上，则从1g小比尺模型[10]进一步向大比尺模型[11]及离心模型[12]试验发展，相关试验系统地研究了盾构失稳演变过程、失稳模式及极限支护压力等问题。可知，以上研究均假定土体为各向同性，并未涉及各向异性土体。

但实际上，土体受天然沉积及土体应力改变等原因，会导致土体强度表现出各向异性。A.CASAGRANDE等[13]推导了土体强度各向异性方程，并得到K.Y.LO[14]的试验验证；Casagrande各向异性公式在边坡稳定[15]、基坑抗隆起稳定[16]及地基承载力[17]方面研究中均已被广泛采用。据笔者所知，对于各向异性地基中盾构开挖面稳定性问题仅有2篇报道，吕玺琳等[18]及Q.PAN等[19]分别基于一定的破坏模式得到其上限解。但在工程实践中，极限平衡解由于受力分析明确，计算公式简单而更被广泛采用，但各向异性地基中盾构开挖面极限支护压力的极限平衡解尚未见报道。

可见，关于盾构开挖面稳定性研究仅针对各向同性土体，各向异性土体的研究对象集中在边坡、基坑及地基承载力等方面，吕玺琳等[18]及Q.PAN等[19]的各向异性土体中的开挖面稳定性研究成果为上限解，但在工程实践中，需要更简单明确的极限平衡解供工程师们采用。在“楔形体-棱柱体”极限平衡模型中考虑盾构开挖面卸荷引起的主应力轴旋转，并基于Casagrande各向异性强度公式，得到盾构开挖面极限支护压力的极限平衡解，最后结合算例分析了各计算参数对极限支护压力的影响。

1 各向异性强度理论

1.1 Casagrande各向异性强度理论

A.CASAGRANDE[13]根据弹性理论推导出黏土强度各向异性的椭圆形方程，得出大主应力方向为任意方向α时的黏聚力cα的表达式：

cα=ch+(cv-ch)cos2α

(1)

式中：ch为施加最大主应力方向为水平向时的土体黏聚力；cv为施加最大主应力方向为竖向时的土体黏聚力；α为主应力方向与竖直方向的夹角。由图1中的几何关系知，α=θ-ψ，其中θ表示计算点土体单元破裂面与竖直方向的夹角，ψ表示计算点土体单元最大主应力方向与破裂面的夹角，采用K.Y.LO[14]试验结果的推荐值ψ=π/4。

图1 固结方向与大主应力方向关系Fig. 1 Relationship between consolidation direction and principal stress

定义各向异性比k=ch/cv，对于土体中某一点，可以认定k是常数。则(1)式又可表示为

cα=cv[k+(1-k)cos2α]

(2)

1.2 考虑土体强度各向异性的盾构开挖面稳定分析模型

盾构开挖过程中，由于支护压力施加不及时或者支护压力施加过小会导致盾构开挖面失稳，形成失稳区域，此时开挖面支护压力小于天然沉积土体的静止土压力，失稳面靠近盾构开挖面区域土体发生侧向卸荷，土体中的应力发生变化，主应力轴也会发生旋转，如图2。图中，C表示上覆土层厚度，D表示隧道直径，ζ为楔形体的滑裂面与竖直方向的夹角，σ1表示土体单元大主应力。

图2 盾构开挖面稳定分析模型主应力方向Fig. 2 Principal stress directions of face stability analysis model of tunnel

2 考虑土体强度各向异性的盾构开挖面极限支护压力研究

2.1 盾构开挖面稳定分析模型

采用G.ANAGNOSTOU等[2]提出的经典“楔形体-棱柱体”极限平衡模型，并假定该模型中正方形abcd的面积与盾构隧道的面积一致，如图3。

图3 “楔形体-棱柱体”极限平衡模型Fig. 3 “edge-prism” limit equilibrium model

取楔形体进行受力分析，可得到开挖面极限支护压力，如图4。楔形体上的作用力包括：自重力G；作用于顶面cdef上的由棱柱体传递来的竖向上覆土压力合力V；作用在斜滑裂面abef上的法向力N1和切向力T1；作用在两侧竖直滑裂面ade和bcf上的2个法向力2N2(由于对称性，法向力2N2=0)和2个切向力2T2(T2方向平行于倾斜滑裂面abef)；作用在开挖面abcd上的极限支护压力σS。

图4 楔形体受力平衡分析Fig. 4 Analysis for force balance of wedge

根据楔形体的受力平衡并结合Mohr-Coulomb破坏准则，可得以下方程：

G+V=T1cosζ+2T2cosζ+N1sinζ

(3)

πD2σS/4+T1sinζ+2T2sinζ=N1cosζ

(4)

T1=cα=ζ-π/4πD2/4cosζ+N1tanφ

(5)

T2=cα=-π/4πD2tanζ/8+N2tanφ

(6)

可得作用在开挖面上的有效极限支护压力：

cv[k+(1-k)cos2(ζ-π/4)]tanζ-

(7)

式中:cv为施加最大主应力方向为竖向时的土体黏聚力；φ为土体内摩擦角；ζ为楔形体的滑裂面与竖直方向的夹角，为变量，不同的ζ将得出不同的σS。

由图5可知，σz沿深度是线性变化，取楔形体侧向竖直面的水平微单元分析，可通过楔形体的侧面竖向应力σz积分运算求得N2：

图5 楔形体侧面竖向应力Fig. 5 Vertical stress of side of wedge

(8)

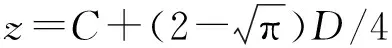
G可由式(9)求得：

(9)

2.2 竖向上覆松动土压力

竖向上覆土压力合力V采用太沙基松动土压力理论计算，取棱柱体水平微单元体(以地表为原点，竖直向下为正，如图6)进行受力平衡分析，其中，G为该水平微单元体的自重，σx、σy分别是x、y方向的侧向土压力，σz分别是竖向应力，τ为侧向摩擦力(τ=Klσx/Klσy)，建立方程可得：

(10)

整理可得：

(11)

图6 棱柱体水平微单元体Fig. 6 Horizontal differential unit of prism

解常微分方程(11)，并代入初始条件z=0时，σz=P0(地表荷载)，可得：

(12)

(13)

则作用在楔形体顶面cdef上的竖向上覆土压力合力V为

(14)

2.3 盾构开挖面极限支护压力

将式(8)、式(9)及式(14)代入式(7)即可得到考虑土体强度各向异性的盾构开挖面极限支护压力，同时此极限支护压力值与楔形体的滑裂面与竖直方向的夹角ζ有关。不少学者[2-3,5]通过先假定ζ的不同值，然后进行迭代计算，求得对应最大支护压力对应下的ζ，此时最大支护压力即为盾构开挖面极限支护压力，笔者计算时也采用此方法。计算时假定基本变量为：土体重度γ=17 kN/m3，施加最大主应力方向为竖向时的土体黏聚力cv=5 kPa，土体内摩擦角φ=30°，隧道埋深C=10 m，隧道直径D=6 m，各向异性比k=1.0，地表荷载P0=20 kPa。

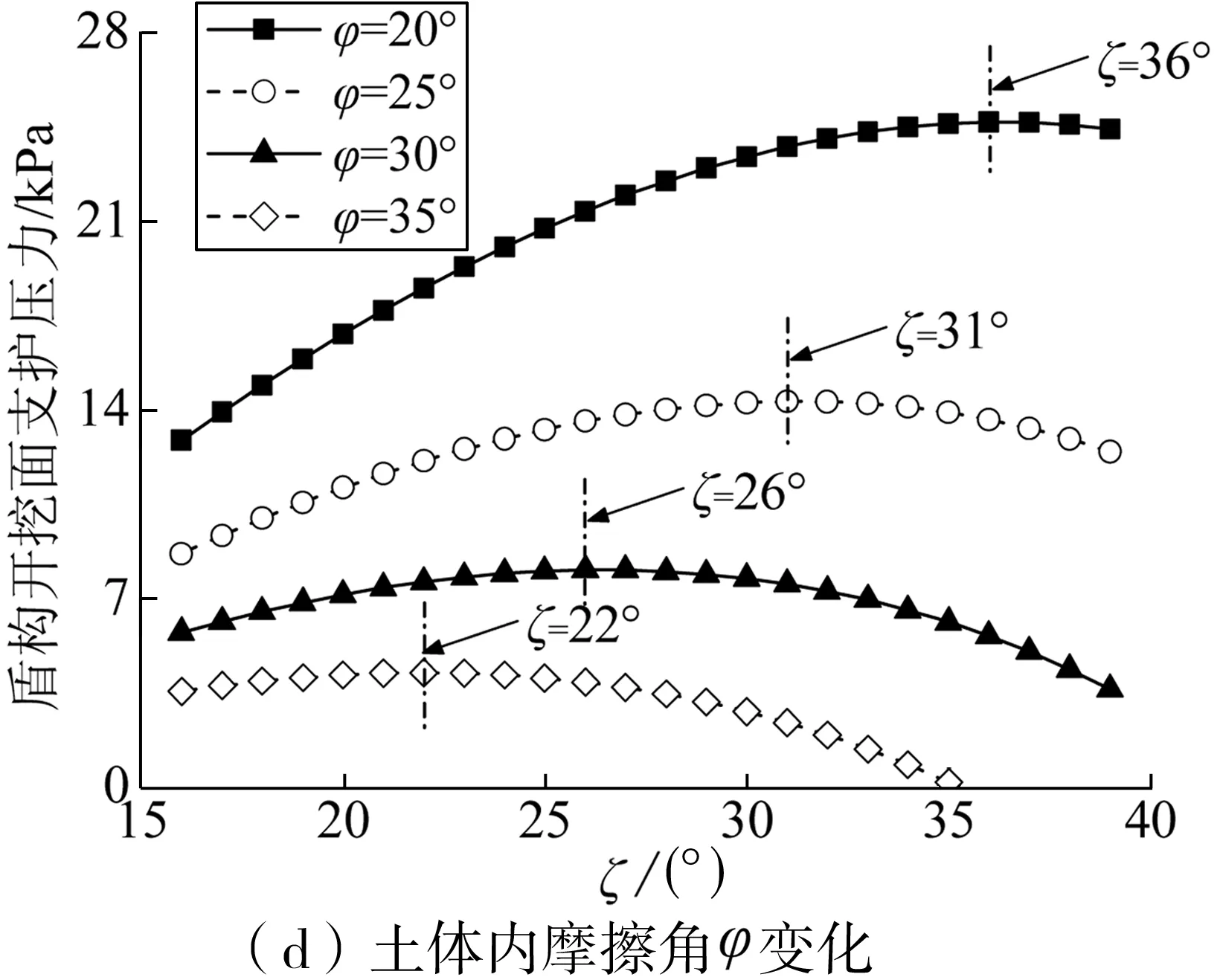
由图7可见，在埋深、隧道直径、土体黏聚力、各向异性比及土体重度变化时，盾构开挖面支护压力均在ζ=26°～27°时最大，此时即为极限支护压力σs。而土体内摩擦角变化时，达到极限支护压力时的ζ为变化的，其随着φ的增大而减小，同时极限支护压力值也相应减小。故可认为极限支护压力对应的ζ是一个与φ有等效关系的变量，这与秦建设[3]的结论是一致的。

3 参数分析

下文基本算例分析中，基本变量如2.3节所述。

图8为各向异性比k变化对盾构开挖面极限支护压力的影响。可见，σS随着k的增大而线性减小。当k=1时，土体强度为各向同性；当k<1时，此时土体强度各向异性表现为大主应力施加为竖直方向时的土体强度，大于大主应力施加为水平方向时的土体强度，此时开挖面极限支护压力大于土体强度为各向同性时的开挖面极限支护压力，这是因为此时滑裂面周边土体对下滑的棱柱体及楔形体的摩擦力相对变小，从而使开挖面极限支护压力变大；当k>1时，则与之相反。在工程实践中，常遇到当k<1的情形，故不考虑土体强度各向异性会使计算所得的极限支护压力偏于不安全。

图9为埋深比C/D变化对盾构开挖面极限支护压力的影响。可见，当k<1时，σS先随着C/D的增大而略有增大，当C/D>1时，σS则趋于稳定，并不随C/D的变化而变化；当k>1时，σS先随着C/D的增大而略有减小，当C/D>1时，σS则趋于稳定；当土体强度各向同性(k=1)时，σS先随着C/D的增大而略微减小，后随着C/D的增大而略微增大，当C/D>1时，σS则趋于稳定。此外，土体强度各向异性越明显，σS随着C/D变化而变化的幅度越大。

图9 埋深比C/D对σS的影响Fig. 9 Influence of C/D on σS

图10为施加最大主应力方向为竖向时的土体黏聚力cv变化对盾构开挖面极限支护压力的影响。可见，σS随着cv的增大而线性减小，且k越大时，减小的幅度越大。

图11为土体内摩擦角φ变化对盾构开挖面极限支护压力的影响。可见，σS随着φ的增大而非线性减小，先φ的增大而较快减小，之后减小速率放缓，最后趋于稳定。此外，在φ较小时，不同k下的σS差别较明显，而随着φ的增大差别逐渐变小。

图10 土体黏聚力cv对σS的影响Fig. 10 Influence of cv on σS

图11 土体内摩擦角φ对σS的影响Fig. 11 Influence of φ on σS

4 结 论

在“楔形体-棱柱体”极限平衡模型中考虑盾构开挖面卸荷引起的主应力轴旋转，并基于Casagrande各向异性强度公式，得到盾构开挖面极限支护压力的极限平衡解，得出的主要结论如下：

1)极限支护压力对应的ζ是一个与土体内摩擦角有等效关系的变量。

2)分析得到了考虑土体强度各向异性条件下盾构开挖面极限支护压力与各向异性比、埋深比、土体黏聚力及土体内摩擦角等因素的关系。

3)盾构开挖面极限支护压力随各向异性比的增大而减小，在各向异性比小于1时，若不考虑土体强度的各向异性，会偏于不安全而导致开挖面失稳事故发生。

4)各向异性比小于1时，盾构开挖面极限支护压力随埋深比的增大而先增大后稳定，各向异性比大于1时，盾构开挖面极限支护压力随埋深比的增大而先减小后稳定，且土体强度各向异性越明显，其随埋深比变化的幅度越大。

5)盾构开挖面极限支护压力随土体黏聚力的增大而线性减小，随土体内摩擦角的增大而非线性减小。

参考文献(References)：

[1] 竺维彬, 鞠世建. 地铁盾构施工风险源及典型事故分析的研究[M]. 广州: 暨南大学出版社, 2009:78-86.

ZHU Weibin, JU Shijian.ResearchonRiskSourcesandTypicalAccidentsinTunnelingConstruction[M]. Guangzhou: Jinan University Press, 2009: 78-86.

[2] ANAGNOSTOU G, KOVáRI K. Face stability conditions with earth-pressure-balanced shields[J].TunnellingandUndergroundSpaceTechnology, 1996, 11(2):165-173.

[3] 秦建设. 盾构施工开挖面变形与破坏机理研究[D]. 南京: 河海大学, 2005.

QIN Jianshe.StudyonFaeeDeformationandCollapseofEarthPressureShieldTunnel[D]. Nanjing: Hohai University, 2005.

[4] 魏纲, 贺峰. 砂性土中顶管开挖面最小支护压力的计算[J]. 地下空间与工程学报, 2007, 3(5): 903-908.

WEI Gang, HE Feng. Calculation of minimal support pressure acting on shield face during pipe jacking in sandy soil[J].ChineseJournalofUndergroundSpaceandEngineering, 2007, 3(5): 903-908.

[5] ANAGNOSTOU G. The contribution of horizontal arching to tunnel face stability[J].Geotechnik, 2012, 35(1):34-44.

[6] CHEN R P, TANG L J, YIN X S. An improved 3d wedge-prism model for the face stability analysis of the shield tunnel in cohesionless soils[J].ActaGeotechnica, 2015, 10(5): 683-692.

[7] LECA E, DORMIEUX L. Upper and lower bound solutions for the face stability of shallow circular tunnels in frictional material = Limites supérieures et inférieures pour la stabilité du front de tunnels circulaires peu profonds, dans un matériau frottant[J].Geotechnique, 1990,40(4):581-606.

[8] MOLLON G, DIAS D, SOUBRA A H. Face stability analysis of circular tunnels driven by a pressurized shield[J].JournalofGeotechnicalandGeoenvironmentalEngineering, 2010, 136(1): 215-229.

[9] 吕玺琳, 王浩然, 黄茂松. 盾构隧道开挖面稳定极限理论研究[J]. 岩土工程学报, 2011, 31(1): 57-62.

LV Xilin, WANG Haoran, HUANG Maosong. Limit theoretical study on face stability of shield tunnels[J].ChineseJournalofGeotechnicalEngineering,2011,31(1):57-62.

[10] KIRSCH A. Experimental investigation of face stability of shallow tunnels in sand[J].ActaGeotechnica, 2010, 5(1): 43-62.

[11] CHENABAA R P. Experimental study on face instability of shield tunnel in sand[J].Tunnelling&UndergroundSpaceTechnologyIncorporatingTrenchlessTechnologyResearch, 2013, 33(1):12-21.

[12] IDINGER G, AKLIK P, WU W, et al. Centrifuge model test on the face stability of shallow tunnel[J].ActaGeotechnica, 2011, 6(2): 105-117.

[13] CASAGRANDE A. Shear failure of anisotropic materials[J].JournaloftheBostonSocietyofCivilEngineers,1944,31(4):74-87.

[14] LO K Y. Stability of slopes in anisotropic soils[J].JournaloftheSoilMechanicsandFoundationsDivision,2014,91(4):85-106.

[15] Al-KARNI A A, Al-SHAMRANI M A. Study of the effect of soil anisotropy on slope stability using method of slices[J].ComputersandGeotechnics, 2000, 26(2): 83-103.

[16] 黄茂松, 于胜兵, 秦会来. 基于上限法的K0固结黏土基坑抗隆起稳定分析[J]. 土木工程学报, 2011, 44(3): 101-108.

HUANG Maosong, YU Shengbing, QIN Huilai. Upper bound method for basal stability analysis of braced excavations inK0-consolidated clays[J].ChineseCivilEngineeringJournal, 2011, 44(3): 101-108.

[17] Reddy A S, Rao K N V. Bearing capacity of strip footing on anisotropic and nonhomogeneous clay[J].Soils&Foundations, 2008, 21(1):1-6.

[18] 吕玺琳, 王浩然. 软土盾构隧道开挖面支护压力极限上限解[J]. 土木建筑与环境工程, 2011, 33(2): 65-69.

LV Xilin, WANG Haoran. Upper bound solution of the Limit support pressure during shield tunneling in soft clay[J].JournalofCivilArchitecturalandEnvironmentalEngineering,2011,33(2):65-69.

[19] PAN Q, DIAS D. Face Stability Analysis for a shield-driven tunnel in anisotropic and nonhomogeneous soils by the kinematical approach[J].InternationalJournalofGeomechanics, 2015, 16(3):04015076.