结合空间相关性的城市热点路段提取方法

刘家良，孙立双(沈阳建筑大学交通工程学院，辽宁 沈阳 110168)

城市热点路段是指交通流量密集且车辆频繁经过的交通路段[1]。为了缓解城市交通压力，需要对城市热点路段进行提取。近年来国内外学者从两个研究角度对其进行了深入研究。一方面是利用出租车的运行速度与运行时间对热点路段进行挖掘。Xu L基于时间-空间相关关系概括得到出行速度和交通量等信息，利用数据立方体定义交通拥堵事件，进而识别出热点路段[2]。B S Westgate引入了贝叶斯模型，通过估算车辆在每个路段的行驶时间，进而对热点路径进行分析[3]。Duan Y使用浮动车的数据，利用样本评估法评估各路段的出行速度，从中识别出频繁拥堵的路段[4]。另一方面是基于路网的交通量密度对热点路段进行研究。Kharrata采用了一种基于移动物体轨迹的聚类方法获取热点路径。该方法通过计算网络中的密集路径，对与密集路径相似的子轨迹进行聚类，最后根据聚类结果获得热点路径[5]。温海平利用路段交叉点和车辆停留点对轨迹进行聚类，结合轨迹数据的语义挖掘，对居民出行的热点路径进行提取[6]。段炼基于DBSCAN聚类算法提出了城市热点路径的搜寻算法[7]。

现有的相关研究大多是利用聚类的方式对城市交通热点路段进行提取，但是对热点路段的提取算法和提取结果验证方面的研究还很少。本文选取大连市2015年3月21日的出租车轨迹数据，对城市道路交通量的全局相关性进行分析，同时基于局部相关统计量对城市热点路段进行提取；采用VISSIM软件对待验证热点路段的交通状态进行仿真模拟；利用行程时间监视器、数据采集器、排队时间计数器采集到的相关数据构建热点路段判别矩阵，采用专家调查法得到3种评价指标的权重矩阵，利用模糊分析法进行热点路段判别；最终得到待验证路段的热点路段隶属程度，从而对热点路段的提取算法和提取结果进行验证[8]。

1 城市热点路段的提取

1.1 道路交通量的全局相关性分析

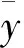
(1)

在给定的显著性水平下，若Moran’s Ⅰ的值大于0，则研究区域内路段间的空间相关性为正。若Moran’s Ⅰ的值小于0，研究区域内路段间的空间相关性为负，研究区域整体呈现出分散模式[11]。通过构造服从正态分布的统计量Z对研究区域内的n个路段间空间相关性的显著性进行检验[12]。其中，显著性检验值Z的表达式为

(2)

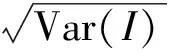
选取2015年3月21日大连市中心城区作为研究区域，根据研究范围内的道路网数据及预处理后的出租车轨迹数据，对城市道路交通量的全局相关性进行计算，得到各个时段的道路交通量的全局Moran’s Ⅰ和全局Z检验值如图1所示。

图1中各时段的全局Moran’s Ⅰ值均大于0.5，表明研究对象呈现正相关聚集分布。对各个时段的Moran’s Ⅰ统计量进行显著性检验，得到各个时段路段的全局Z检验值均大于正态分布函数在5%显著性水平下的临界值1.96。因此，研究区域内路段的交通量在空间上呈现显著性较强的正相关。

1.2 基于局部相关统计量的热点路段提取

为了对研究区域内的热点路段进行提取，首先要计算每条道路的局部Moran’s I值。其计算公式为

(3)

选取大连市的中心城区2015年3月21日的道路网数据及各路段的交通量数据进行热点路段的提取。分别选取8:00—9:00、12:00—13:00、18:00—19:00 3个时段，根据式(3)计算研究区域内所有路段的局部Moran’s Ⅰ值，并进行显著性检验，最终得到5%显著性水平下2015年3月21日不同时段的热点路段分布图，如图2所示。

图2 3月21日的热点路段分布

通过分析可以发现热点路段的数量随时段的不同而不同，且主要分布在如中山路、疏港路、东联路、虹港路等城市主干道路上；同时城市的热点路段在同一时间段内的分布有较大的相似性。

2 热点路段的提取算法验证

选取2015年3月21日8:00—9:00的热点路段——大连市黄河路作为验证对象，采用VISSIM软件对验证对象的交通状态进行仿真模拟。即首先对路段进行设置，热点路段的验证对象为东西向的大连市黄河路(双向6车道)，在该试验路段的南北方向上有盖州街(双向单车道)、升平街(单向双车道)和广平街(单向双车道)3条支路段。图3为大连市黄河路的示意图，图中的编号表示交通量输入输出位置的点号，箭头表示车辆的行驶方向，A、B、C表示信号灯编号，a、b、c表示数据采集点编号。

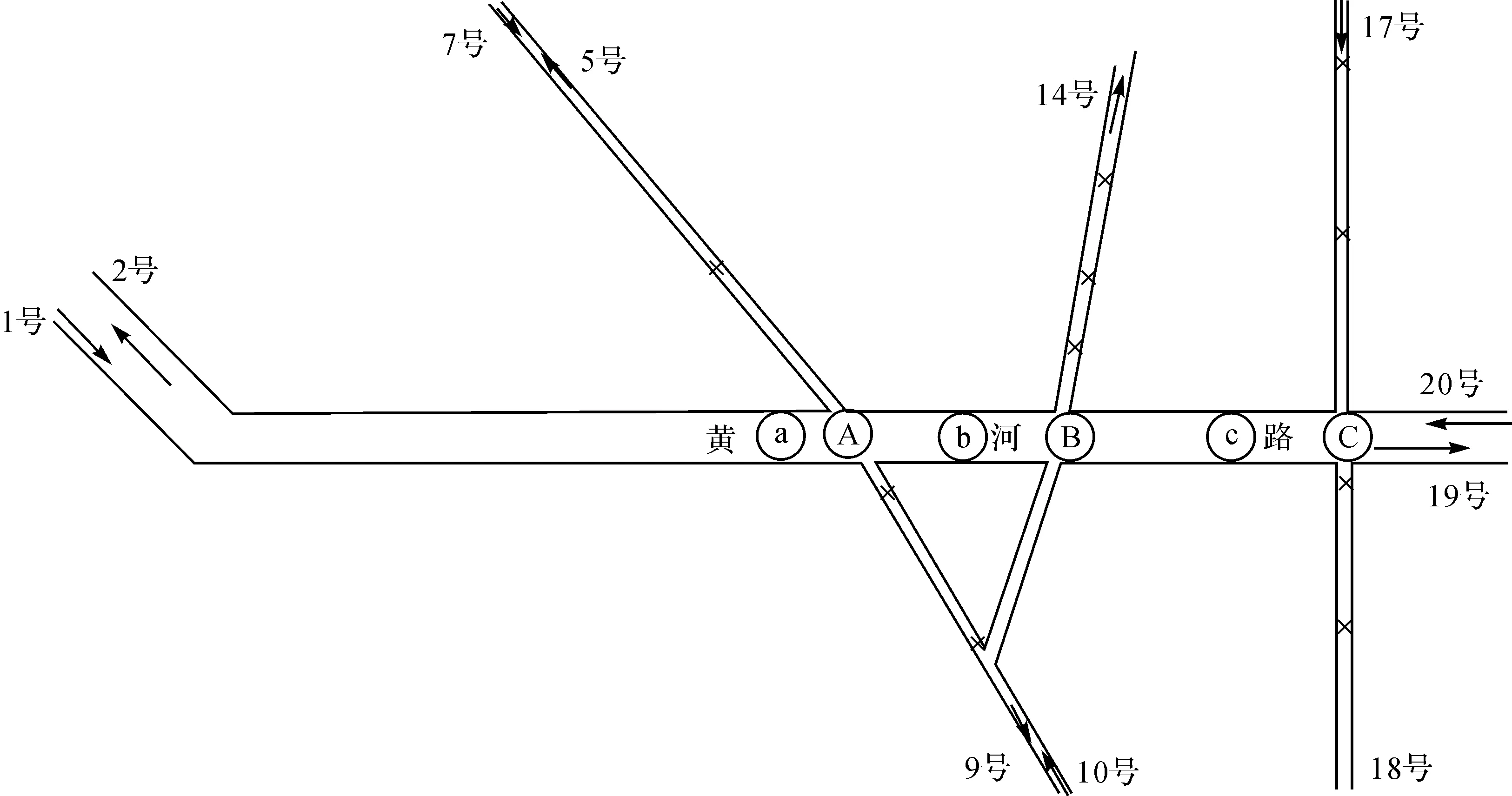
图3 大连市黄河路的路段示意图

然后对数据采集点进行设置。在断面a、b、c处分别对路网添加行程时间监视器、数据采集器和排队时间计时器。在3600 s仿真时间内，以10 s为间隔采集通过断面的车辆数。同时对Oracle数据库中的路段交通量数据进行提取，得到2015年3月21日8:00—9:00大连市黄河路的各个出入口的交通量输入情况见表1。

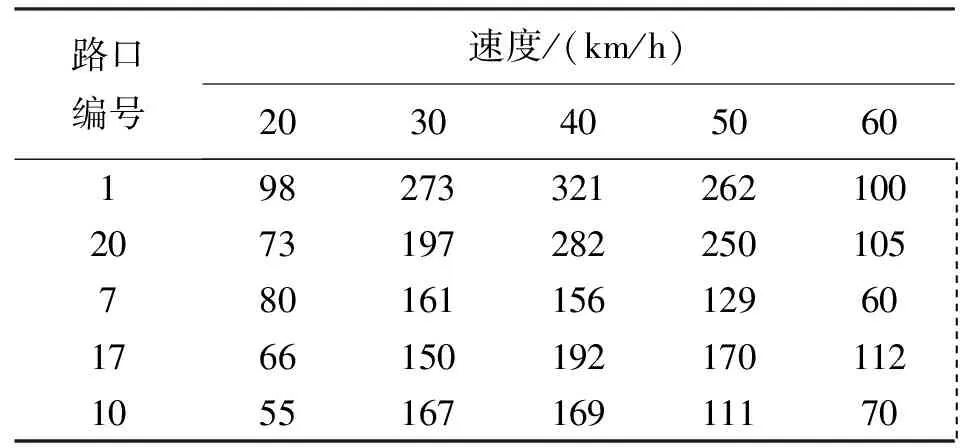
表1 各路口在不同速度条件下的交通量 辆

最后对交通信号灯进行设置，在断面A、B、C处分别添加信号灯。模拟路段中的交叉口共有3个，分别为黄河路-盖州街交叉口、黄河路-升平街交叉口、黄河路-广平街交叉口，其中黄河路-盖州街交叉口的配时方案见表2。

结合以上建模参数，得到2015年3月21日8:00—9:00的大连黄河路的VISSIM交通仿真后状况如图4所示。

由于状态属性与评价指标之间存在模糊关系，因此根据2012年我国《城市道路交通管理评价指标体系》中A级城市主干路段的分级标准，设定各个指标隶属度函数的各级阈值的范围。选取交叉口的时间延误、路段行驶时间和浮动车行驶速度作为判别模型的评价指标。将热点路段的程度划分为热点路段、次热点路段和非热点路段[15]。构造出各个指标的隶属度函数如图5所示。

表2 黄河路-盖州街交叉口信号配时方案 s

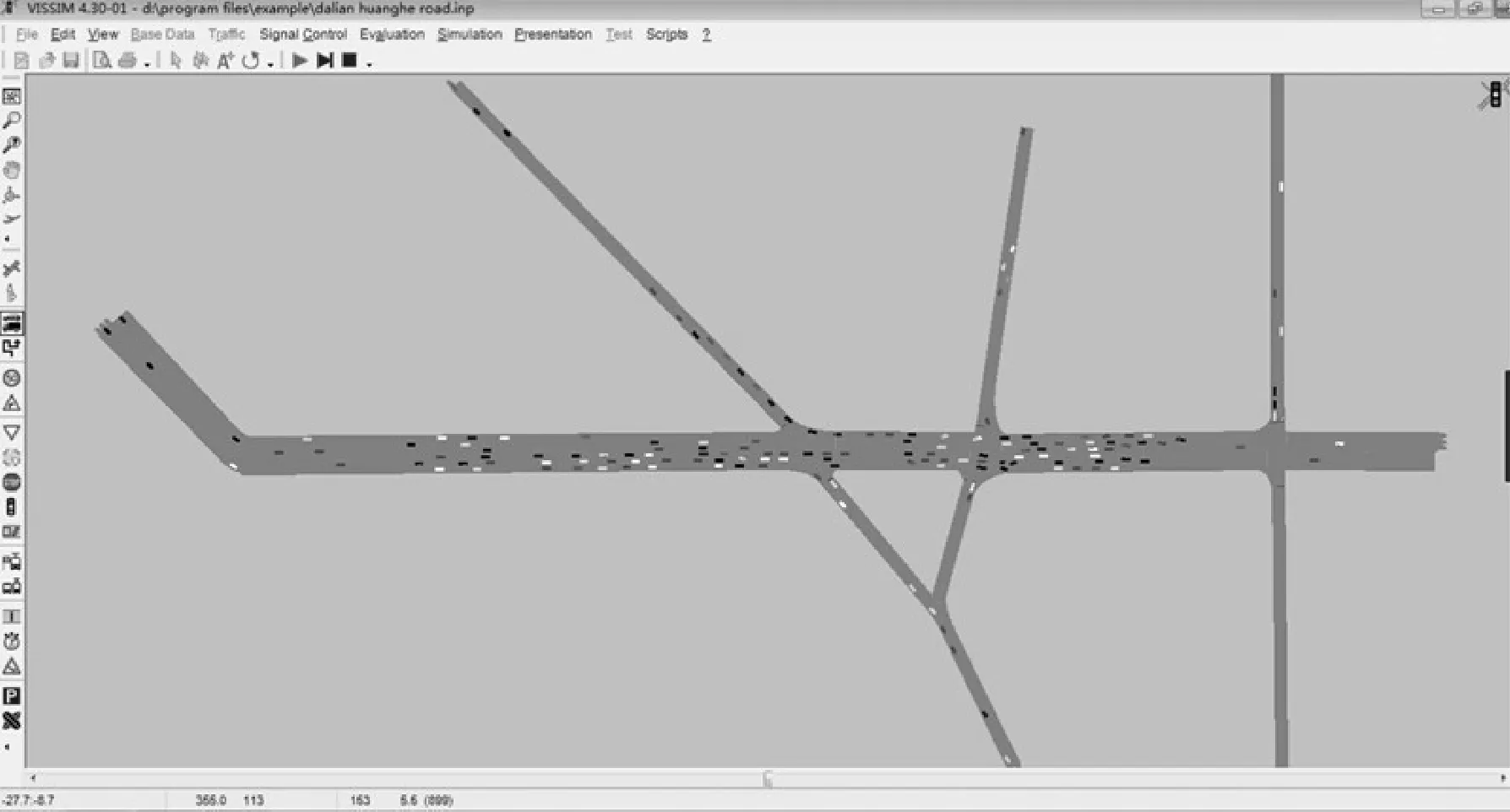
图4 大连黄河路VISSIM交通状态仿真状况

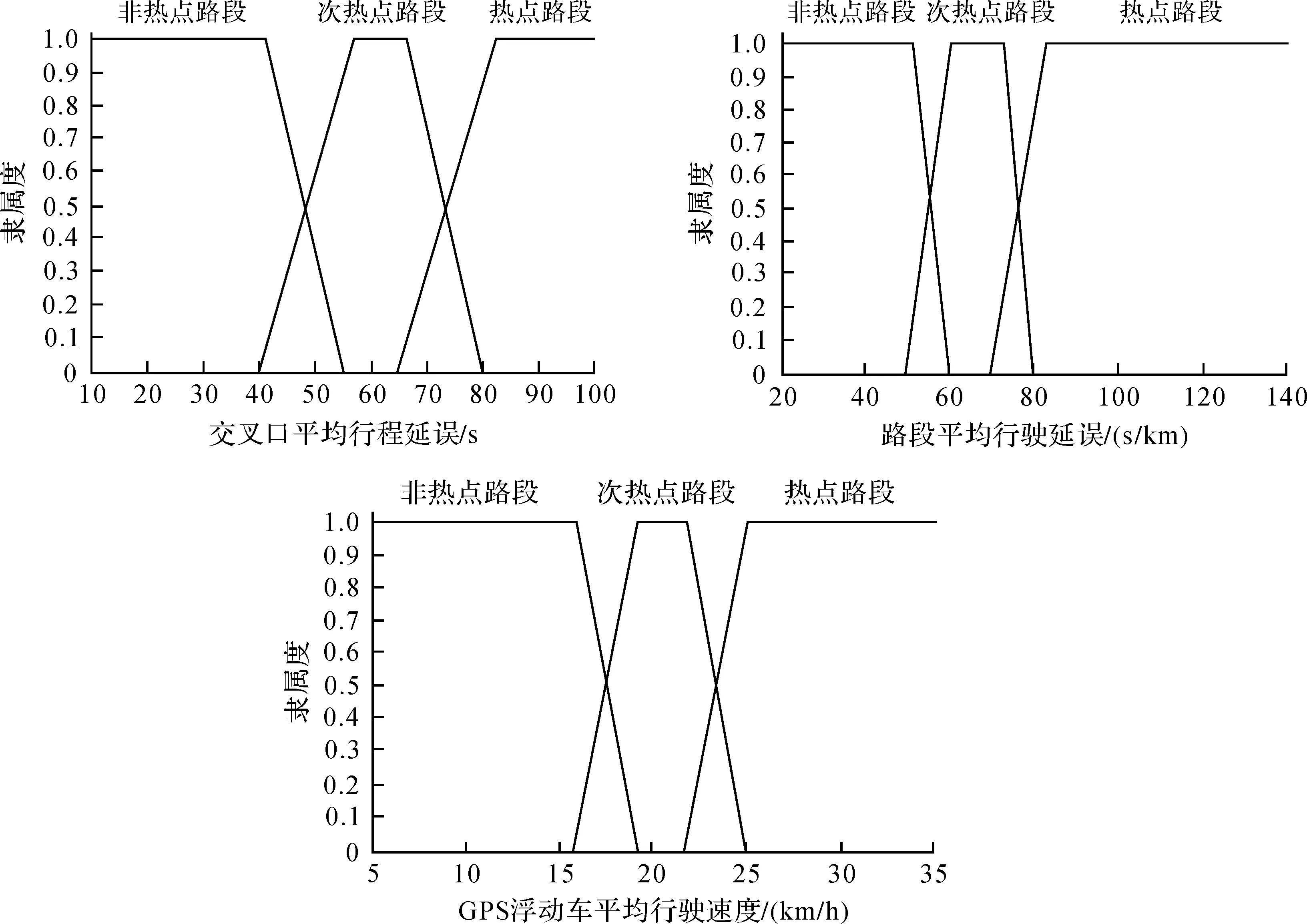
图5 交叉口的时间延误、路段行驶时间延误及车辆行驶速度的隶属度函数

将浮动车平均行驶速度、路段的平均行程延误和交叉口平均行程时间延误分别代入各自的评价集隶属函数中，得到浮动车平均行驶速度判别结果R1=[μA(V)μB(V)μC(V)]、路段的平均行程延误判别结果R2=[μA(V)μB(V)μC(V)]、交叉口平均行程时间延误结果R3=[μA(V)μB(V)μC(V)]。本文采用专家调查法对各评价指标对应的权重系数进行评价赋值，得到3种指标的权重矩阵A=[a1a2a3]。其中a1为路段行驶速度的权重系数，a2为路段的平均行程延误的权重系数，a3为交叉口平均行程时间延误的权重系数。通过对3种指标的权重矩阵A和判别矩阵R进行模糊判断，得到热点路段的判别结果为[16]

[b1b2b3]

(4)

式中，b1为热点路段的隶属程度；b2为次热点路段的隶属程度；b3为非热点路段的隶属程度。经过VISSIM对待验证路段交通状态进行仿真，可以得到2015年3月21日8:00—9:00的大连市黄河路路段行驶时间延误为85(s/km)，浮动车平均行驶速度为20(km/h)，交叉口平均行驶时间延误为76.5 s。

最后，根据热点路段的判别模型，将黄河路路段参数指标值代入模型中，通过对判别矩阵和权重矩阵进行模糊判断，得到待验证路段的非热点区域隶属程度为0.276，次热点区域隶属程度为0.212，热点区域隶属程度为0.512，依据最大隶属重要度原则，把隶属度最大值所对应的热点路段的状态属性作为判别目标的最终判别结果。由此可以判别出2015年3月21日8:00—9:00的大连市黄河路为热点路段。

3 结 语

(1) 本文采用空间相关性分析的方法实现了对大连市2015年3月21日交通热点路段的提取，得到了一天中3个特征时段的热点路段空间分布图。通过分析可以发现：研究区域内路段的交通量在空间上呈现显著性较强的空间正相关性。不同特征时段内交通热点路段主要分布在城市的主干道路上，其聚集程度随时段的变化而不断变化，且高度聚集的交通热点路段在同一时段内的分布存在较大的相似性。

(2) 选取了2015年3月21日8:00—9:00的热点路段大连市黄河路作为验证对象，采用VISSIM软件对该路段的交通状态进行仿真模拟。最终得到该路段的热点路段隶属程度为0.512，判定该路段为热点路段。表明基于空间相关性的城市热点路段提取算法合理有效。

参考文献：

[1] 杨晞.大连城市交通拥堵的治理对策研究[D].大连:大连海事大学,2015.

[2] XU L，YUE Y，LI Q.Identifying Urban Traffic Congestion Pattern from Historical Floating Car Data [J].Procedia-Social and Behavioral Sciences，2013，96:2084-2095.

[3] WESTGATE B S，WOODARD D B，MATTESON D S，et al.Travel Time Estimation for Ambulances Using Bayesian Data Augmentation [J].Annals of Applied Statistics，2013，7(2):1139-1161.

[4] DUAN Y，LU F.Robustness of City Road Networks at Different Granularities[J].Physica a Statistical Mechanics & Its Applications，2014，411(411):21-34.

[5] KHARRAT A，POPA I S，ZEITOUNI K，et al.Clustering Algorithm for Network Constraint Trajectories[C]∥Headway in Spatial Data Handing，International Symposium on Spatial Data Handling.Montpellier：DBLP,2008:631-647.

[6] 温海平.基于轨迹聚类的热点路径分析方法研究[D].重庆：重庆邮电大学，2011.

[7] 段炼,李峙,胡宝清.时空约束下的热点路径空间分布检测算法[J].计算机工程与设计,2014,35(3):861-866.

[8] 徐建.基于空间计量模型的交通事故分析与预测[D].南京:东南大学，2014.

[9] 张树德.基于复杂网络理论的城市道路网络脆弱性研究[D].哈尔滨:哈尔滨工业大学,2014.

[10] 田薇,张锦明,龚建华.面向不同主题的交通大数据可视分析[J].测绘科学技术学报,2017,34(1):102-105.

[11] 崔艳超，周刚.Spark平台上基于K-Means算法的热点路径发现方法研究[J].信息工程大学学报，2016，17(6):743-747.

[12] 刘康,仇培元,刘希亮,等.利用词向量模型分析城市道路交通相关性[J].测绘学报,2017,46(12):2032-2040.

[13] 桂新,秦海波,王胜平,等.基于相关系数迭代法的水下地形测量时间延迟探测方法研究[J].测绘通报,2015(5):57-59.

[14] 毛海霞,田岩,范小朋,等.基于时空车流灰度的城市交通热点分析[J].地理信息世界,2016,23(3):13-19.

[15] 朱海涛.基于出租车GPS数据的城市主干道路交通状态判别[D].哈尔滨:东北林业大学，2016.

[16] 董琦.基于VISSIM的环形交叉口与信号控制交叉口型式选择研究[D].西安:长安大学，2014.