马尔科夫链优化Richards曲线的沉降预测模型
赵亚红,贺黎明,王金星,郝延锦,牛芩涛(. 华北科技学院建筑工程学院,北京 060; . 东北大学测绘遥感与数字矿山研究所,辽宁 沈阳 089; . 北京帝测科技股份有限公司,北京 000)
国家经济的快速发展带动各种建筑工程不断涌现,而建筑物的安全问题不容忽视。沉降监测是衡量建筑物安全与否的一项重要工作。监测分析的最终目的是对建筑物进行移动变形预测,为防灾减灾及工程设计提供参考依据。沉降预测主要是根据一部分实测数据,选择合适的模型,进行模型参数求解,从而进行沉降预测。其沉降趋势根据建筑施工过程经历慢速增长、快速增长再慢速增长直至趋于稳定的过程,沉降曲线呈S形。可以描述这种曲线的模型有多种,如泊松曲线、Gompertz曲线、Logistic、Richards曲线等。每种单一模型都具有各自的优缺点,如泊松曲线要求等时间间隔沉降序列;Gompertz、Logistic模型只能用来描述S曲线的某一特定部分,不能完整模拟建筑物沉降的全过程;Richards模型属于生长曲线模型,在某种特定情况下不仅包含了Gompertz、Logistic模型,且不需要序列为等时间间隔序列,对S曲线的描述能力很强,其准确性达到了很高水平[1-2],因此被广泛应用。但是每个工程地质与施工荷载情况不同,其建筑物沉降趋势也不尽相同,单一方法不能很准确地预测其沉降趋势,因此将多种方法组合进行沉降预测应运而生。龙四春等利用平移反幂法的特征值求权,进而对Logistic与Richards模型进行加权组合[3],通过实例验证了加权组合模型的优越性;任云志等利用BP修正Richards模型预测残差[4],从而提高了预测精度;胡晓阳等将Logistic及Verhulst进行最优加权组合预测[5];刘光秀等将灰色Gompertz进行最优加权组合预测[6]等。通过多种方法组合可以充分利用原始序列中的有用信息,单一模型的优势得到互补,从而能更好地预测建筑物沉降的发展趋势。由于建筑物沉降受到多方面因素的影响,其变形机理复杂且具有一定的随机性,而马尔科夫理论研究对象为随机性动态变化过程[7-9],可以通过其概率转移矩阵反映数据序列随机波动情况,因此可以用来研究建筑物沉降趋势。本文在Richards生长曲线模型及马尔科夫理论基础上,建立马尔科夫链修正Richards曲线的沉降预测模型,并结合安阳市某高层建筑物沉降变形的实测数据,对马尔科夫链优化后的Richards模型进行验证和分析。
1 马尔科夫链优化Richards曲线建模原理
1.1 Richards曲线模型
Richards增长模型是描述生物经历慢速增长、快速增长、减速增长直至趋于稳定的生长规律,其曲线呈S形,这也与建筑物沉降变形的时间-沉降量曲线一致,因此被广泛应用于地基沉降及岩土力学[10]。其函数模型为
S(t)=S0(1-αe-βt)1/1-γ
(1)
式中,S(t)为地基t时刻的沉降量;S0为地基沉降量的极限值;α为地基形变初始值参数;β为地基形变的增长速度参数;γ为地基变形曲线形状参数。其中S0、α、β、γ为模型的4个未知参数。当γ→1,式(1)变换为Gompertz模型;当γ=2时,式(1)变换为Logistic模型。由此可以看出Richards模型包含了地基沉降预测中常用的Gompertz及Logistic模型。
该模型方程为非线性方程,参数的解法有四点法、三段法[11]、差分最小二乘[12]、遗传算法[13]、粒子群算法[14]等。四点法、三段法需要对时间序列进行等分,在较短的时间序列不适用,差分最小二乘需要对后一项与前一项求差再取对数,这就要求沉降序列是单调递增序列,然而实际中沉降序列由于各种原因,可能出现波动或“跳变”,这种情况以上 3种算法均不适用。遗传算法、粒子群算法在非线性模型参数最优解中能取得较理想的效果[14-15],但是算法较为烦琐,需要有一定的编程基础。而Matlab平台中自带的函数fminsearch可以解决无约束非线性最优解问题。因此本文利用fminsearch函数,以拟合值与实测值误差平差和最小为原则,求解该模型的4个参数,方法简单,操作方便。
1.2 马尔科夫链优化Richards建模预测
马尔科夫理论描述的是一个随机的动态变化过程,可以把实测沉降量序列当作随机过程,通过研究沉降量的初始概率及转移概率矩阵,来预测未来沉降量的所处状态,并且未来的状态独立于以前的状态,仅依赖于当前的状态。通过马尔科夫链修正Richards预测模型的预测残差,二者优势得到互补。其步骤如下:
首先,依据实际情况计算Richards模型拟合值与实际沉降观测值之间的残差,按式(2)计算相对误差ξ(t),并对相对误差进行归类,划定马尔科夫链状态区间。
(2)
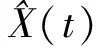
式(3)表示第t时刻的拟合相对误差ξ(t)处于第i种状态Ei,状态Ei的上下界分别由a1i和a2i表示。因此,总的状态集合表示为E=(E1,E2,…,Es)。
ξ(t)∈[a1i,a2i] (i=1,2,3,…,s)
(3)
其次,计算一步状态转移概率矩阵P
(4)
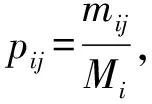
设当前预测值的初始状态向量为ε0,由状态转移概率矩阵可知经过k步转移后的状态向量为ε0Pk。但是在实际预测中,一般情况下只考虑一步转移概率矩阵[9]。若预测对象的状态处于Ek,仅需考虑第k行到下一行的概率矩阵,若max(Pkj)=Pki,那么就可以把k状态转向i状态为最大概率,即预测对象出现在第i状态。若出现转移矩阵P中k行有两个或两个以上概率相同或相近时,状态转移方向不确定,此时考虑两步或n步转移,然后再按照上述方法进行状态预测。
最后,确定预测沉降量所在的状态区间后,取均值可得预测值方程
(5)
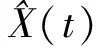
2 精度评定方法
马尔科夫链优化Richards模型预测精度,首先计算实测值与预测值的残差,以及相对误差,然后利用均方根误差(RSME)与平均绝对百分比误差(MAPE)进行评定,具体计算方法为
(6)
(7)
3 工程实例应用
以文献[16]中安阳市某小区17层高层住宅为例,采用长螺旋CFG桩复合地基,自建筑物出地面开始进行定期监测,在主体施工期间每20 d观测一次,观测9次,此后观测间隔变长,观测次数相对减少,共观测13期。1#楼沉降观测点的累计沉降量见表1 。
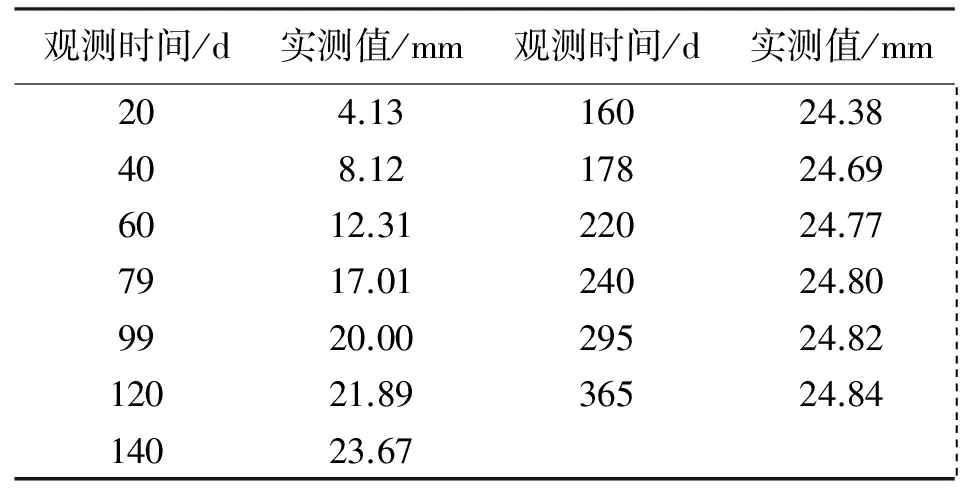
表1 实测沉降量
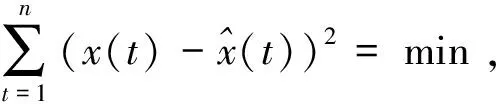
S(t)=25.285 5(1+0.605 1e-0.027 7t-6.215
式中,t=1,2,…,10。拟合值及相对误差见表2。
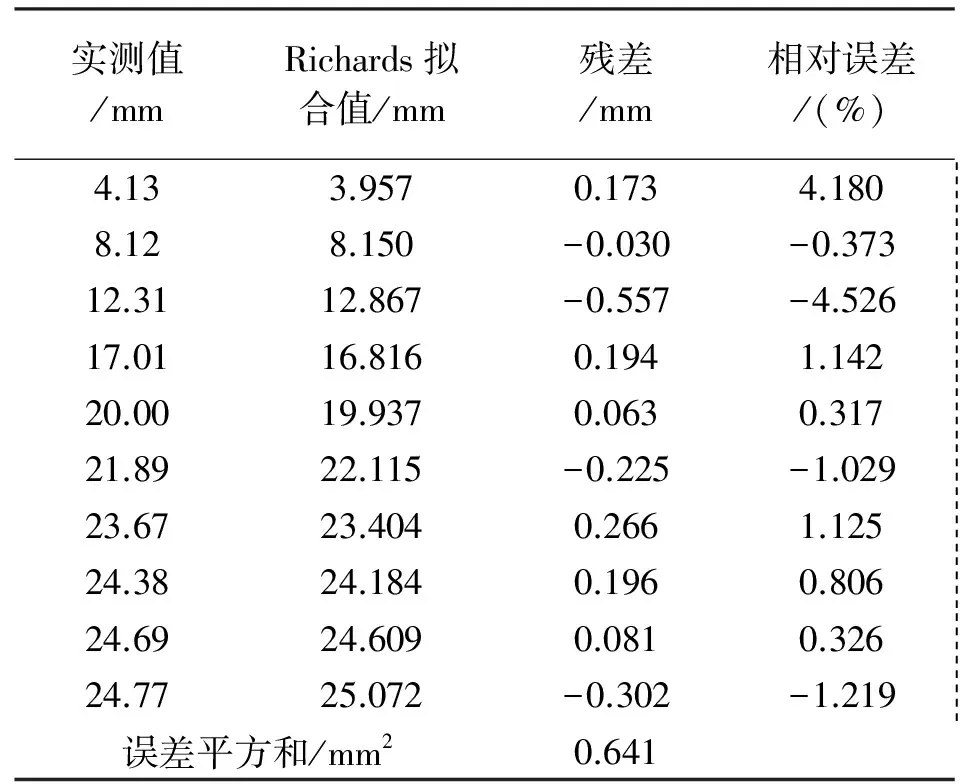
表2 Richards模型拟合值与相对误差
然后利用马尔科夫链优化Richards模型,根据模型拟合相对误差划分状态区间,可以划分3个状态区间[-5,-2]、[-2,1]、[1,5],各个拟合值的状态分布见表3。

表3 各拟合值所处状态
根据式(4),可以计算一步状态转移矩阵
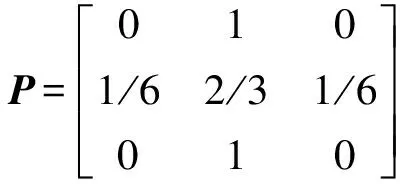
然后预测第11期沉降量,第10期拟合沉降量位于状态E2,其初始状态向量ε0=[0 1 0],经过一步转移后的状态转移向量为
从而可以得出第11期预测沉降量出现在E2状态。Richards模型预测11期沉降量为25.162 6 mm,根据式(5)求得马尔科夫修正后新的预测值
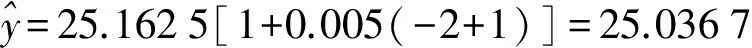
预测值的相对误差为-0.946%。
去掉第1期拟合沉降量,以第2期至11期预测值来预测第12期沉降量,计算相对误差,重新划分区间为[-5,-2]、[-2,0.5]、[0.5,2],限于篇幅,不再详细列出状态区间,计算一步转移矩阵

第11期预测值处于E2状态,通过计算可得第12期预测值也处于E2状态,可以得到马尔科夫优化Richards模型的第12期预测值。以此类推,去掉第2期拟合值,利用第3—12期预测值,重新划分状态区间,可以得到第13期预测值。具体结果见表4。
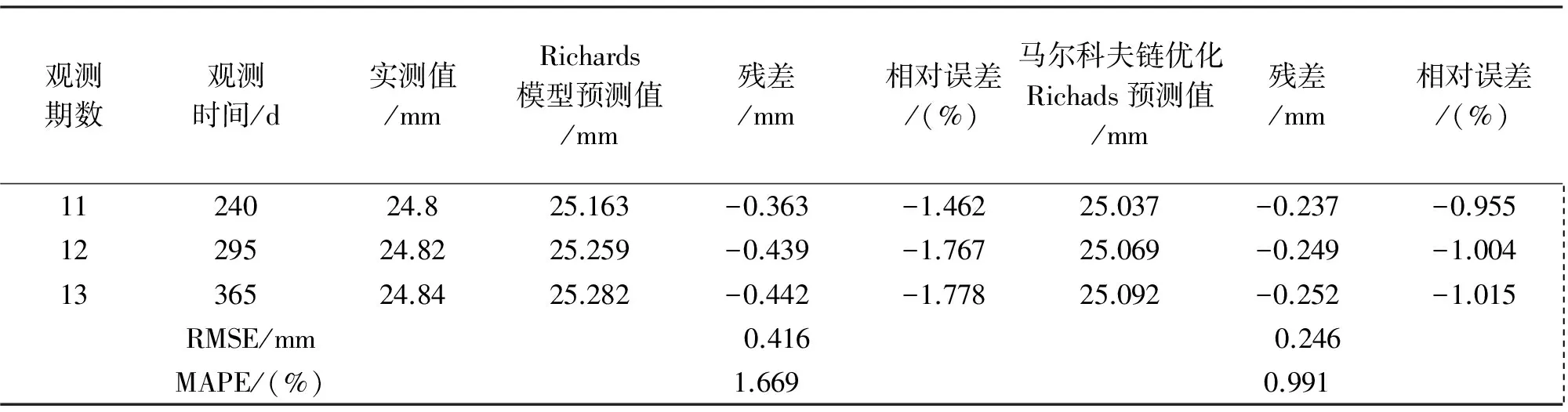
表4 各模型预测值及精度
从表4可以看出,经过马尔科夫优化后,Richards预测结果精度有了显著的提高,残差减小,预测均方根误差达到0.246 mm,平均绝对百分误差MAPE达到0.991%,两个精度指标都有了一定程度的提高。图1后3期预测值经过马尔科夫链修正后,相对误差向0方向靠近,表明经过马尔科夫优化后的模型,预测精度更高,预测结果更能贴近建筑物沉降趋势。
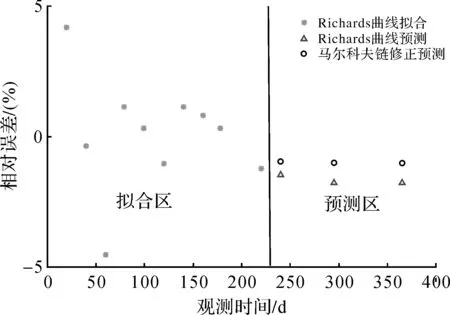
图1 相对误差分布
4 结 论
(1) 在Richards生长曲线及马尔科夫理论基础上,建立了马尔科夫链优化Richards曲线的沉降预测组合模型。该模型利用一定的数据序列,以拟合值与实测值误差平方和最小为原则,利用Matlab中的fminsearch函数,获得Richards曲线参数最优解,再利用马尔科夫理论修正Richads曲线预测残差。
(2) 利用Matlab自带函数fminsearch对Richards曲线进行参数估计是可行的,并且不受任何限制条件影响,方法简单,操作方便,为Richards模型参数求解提供了一种新方法。
(3) 实例表明,该组合预测模型的预测均方根误差及平均绝对百分误差有了一定的减小,预测精度有了一定的提高,可以应用于建筑物沉降预测。
参考文献:
[1] 王正帅,邓喀中.采动区地表动态沉降预测的Richards模型[J].岩土力学,2011,32(6):1664-1668.
[2] KOYA P R,GOSHU A T.Generalized Mathematical Model for Biological Growths[J].Open Journal of Modelling and Simulation,2013,1(4):42-53.
[3] 龙四春,彭强,黄两宜,等.一种加权Logistic-Richards组合模型的地表沉降预测方法[J].大地测量与地球动力学,2015,35(5):821-824.
[4] 任云志,周飞,陆鹏宇.基于Richards-BP模型的地表沉降特征预测模型研究[J].交通科技,2015(1):89-92.
[5] 胡晓阳,王连俊,张光宗.Logistic及Verhulst预测模型在路基沉降预测中的拟合研究[J].铁道标准设计,2013(9):1-4.
[6] 刘光秀,曹海莹,李玉根.灰色-Gompertz组合模型在软土路基沉降预测中的应用[J].中国科技论文,2016,11(13):1488-1491.
[7] 刘淑官,黄声享,徐北海,等.基于无偏灰色马尔科夫链的基坑沉降预测研究[J].测绘地理信息,2015,40 (4):10-13.
[8] 邹进贵,肖扬宣,张士勇.马尔科夫链改进的ARIMA-BP神经网络模型研究[J].测绘地理信息,2016,41(4):32-36.
[9] 杨世安.优化的灰色马尔科夫模型在建筑物沉降预测中的应用[D].南昌:东华理工大学,2014:21-35.
[10] 王军龙.围岩变形预测的Richards模型及变形发展趋势分析[J].公路工程,2014,39(3):145-148.
[11] 程毛林.Richards模型参数估计及其模型应用[J].数学的实践与认识,2010,40(12):139-143.
[12] 乔钰,徐文科.Richards增长曲线的参数估计[J].哈尔滨师范大学自然科学学报,2015,31(5):23-26.
[13] 燕振刚,胡贺年,李广.基于粒子群优化算法的Richards模型参数估计和算法有效性[J].计算机应用,2014,34(10):2827-2830.
[14] 王江荣.Richards生长曲线模型在大坝变形监测数据处理中的应用[J].矿山测量,2015(5):59-61,64.
[15] 王钧.基于变步长果蝇优化算法的Richards模型参数估计[J].计算机工程与设计,2017,38(9):2402-2406.
[16] 张庆伟,肖建清.GM(1,1)与Verhulst模型在地基沉降预测中的适用性比较[J].沈阳工业大学学报,2014,36(6):716-720.

