相机检校的迭代处理方法
崔璨璨,汪佳丽,马振玲(上海海洋大学海洋科学学院,上海 201306)
普通数码相机(非量测相机)因其成本低廉、便于携带等优点,在摄影测量作业中得到越来越广泛的应用[1]。相机检校问题在相机发明后用于量测应用后就存在,其结果很大程度上影响数字摄影测量后续工作的处理精度[2-3]。当前已有大量摄影测量学者进行了非量测相机检校方面的研究[4-8],但仍存在易受操作空间和拍摄角度的影响,稳健性较差[4-5]、缺少主点修正和其他畸变修正[6]、无法保证相机稳固性[7]、忽略了影像边缘区域检校[8]等问题。此外,基于计算机视觉的检校方法虽然保证了精度,但对标定板要求较高,在实际应用中有着局限性[9-11]。因此,本文结合前人的研究成果[8,12],主要从摄影测量的角度对非量测相机的检校进行探讨,并且提出了相机的迭代检校思路。
首先,针对传统检校场地造价昂贵、对标志点量测精度高、对周边环境要求高等问题,本文提出不需要额外建设投入,可以利用现有条件快速建立简易实用的相机检校控制场,并且通过试验证明此类检校场行之有效,能满足一定的需求。其次,针对通常的相机检校方法(以下简称常规检校法)检校后由于使用模型不足仍然存在残留畸变误差的问题,本文提出相机检校的迭代处理思路(以下简称迭代检校法),并且利用简易室外检校场验证迭代检校法。最后,在无控制点情况下,通过增加约束条件把相机检校模型纳入自由网平差,同样按照上述相机迭代检校处理的思路实现无控制点的相机迭代检校。通过设计各种试验比较分析了常规检校法和迭代检校法,验证了新提出的相机迭代检校法既适用有控制点条件的相机检校,也适用于无控制情况下的相机检校。
1 检校场建立与相机检校
1.1 检校场建立
本文构建室外检校场因其能够充分考虑摄影测量的实际工作条件,使相机检校最大限度地接近实际工作环境。一些室外检校场需要在一个或多个建筑物上布设一定数量的人工标志点[13],不仅成本较高,也给标志点布设增加了工作难度。在构建非量测数码相机二维平面检校场时,考虑到建筑物变形小、格网点清晰明确、拍摄方便等优点,因此选用一面由几何形状规则的砖块所组成的纹路清晰的墙面作为检校场,这样既节省了成本,也避免了布设人工标志点的难度,并且容易找到大量均匀分布的控制点点位。本文选取由规则砖块构成的墙面作为简易检校场,把砖块角点作为控制点。检校场的控制点坐标采用独立坐标系,使用徕卡全站仪进行多次量测取平均值作为最后量测坐标,共选用188个控制点进行检校试验与精度评定,点位精度优于2 mm,控制点均匀分布在墙面,区域覆盖了影像的绝大部分面积。本文构建的室外检校场及量测的控制点点位分布如图1所示。

图1 简易室外相机检校场(二维平面检校场及控制点点位分布)
1.2 相机常规检校法
本文中提到的常规检校法是指使用现有相机检校模型进行畸变系数计算和影像校正。现有相机检校模型是指已经提出且广泛应用于相机检校的模型。相机检校的主要目的是确定相机光学畸变差。光学畸变差指摄像机物镜系统设计、制作和装配所引起的像点偏离其理想位置的点位误差[14],是影响像点坐标质量的一项重要误差,为了正确恢复摄影时的光束形状,需准确求解光学畸变系数。常见的畸变类型[13,15]可以归纳为以下3类。
1.2.1 径向畸变差
径向畸变主要是由于相机镜头的镜片在加工过程中产生的误差所引起的。径向畸变差的表达式为
Δr=k1r3+k2r5+k3r7
(1)
(2)
(3)
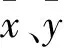
1.2.2 偏心畸变差
偏心畸变差在数量上与径向畸变相比要小很多,但偏心畸变同时具有径向偏差和切向偏差,它是由于相机的光学系统中心与几何中心不一致造成的,用多项式表达为
(4)
式中,Δxd、Δyd为偏心畸变差;p1与p2均为切向畸变系数。
1.2.3 平面内畸变差
平面内畸变主要是主光轴偏移所导致的x轴和y轴比例不一致和坐标轴的不正交这两个因素的影响。平面内畸变差的表达式为
(5)
式中,Δxf、Δyf为平面内畸变差;b1为在像元大小不均匀的情况下,x方向尺度比例因子;b2为在像素阵列不正交情况下的裁切系数。
Australis模型考虑了相机物镜的径向畸变、偏心畸变、平面内畸变,适用于二维平面检校场和三维空间检校场,如下式为
(6)
式中,Δx、Δy分别表示像空间坐标系下x、y方向的物镜畸变差。
将式(3)、式(4)、式(5)代入式(6),Australis模型可表示为
(7)
式中,Δx0、Δy0为相机主点改正量;c为主距;Δc为主距改正值。
为叙述方便,本文中将只考虑2个偏心畸变系数的模型称为“二号模型”,将只考虑含3个径向畸变系数的模型称为“三号模型”,将同时考虑2个偏心畸变和3个径向畸变系数的模型称为“五号模型”,将同时考虑径向畸变、偏心畸变、平面内畸变等7个系数的Australis模型称为“七号模型”。
1.3 相机迭代检校法
针对相机检校常规法对残留畸变没有再进行分析处理的问题,本文提出了相机检校迭代处理的思路(即迭代检校法)。通过对原始影像多次采用同一检校模型或不同模型组合,经过迭代处理达到对影像畸变校正的目的,每次迭代后利用新得到的畸变系数对影像进行校正,把校正后重采样得到的影像作为下次迭代的输入影像,重新采样检校模型进行检校,经过如此多次迭代处理,根据预先设置的畸变系数变化阈值决定是否终止迭代。迭代检校法虽然具有多组检校畸变系数,需要对影像多次重采样,但是多次重采样仅发生在检校过程中,一旦检校完成,在实际影像的检校可以通过一系列计算,确定畸变的最后几何位置,只进行一次影像重采样,从而可以避免多次重采样造成的信息丢失和清晰度减低,同时也可以减少多次影像校正的工作量。相机迭代检校法原理如图2所示。
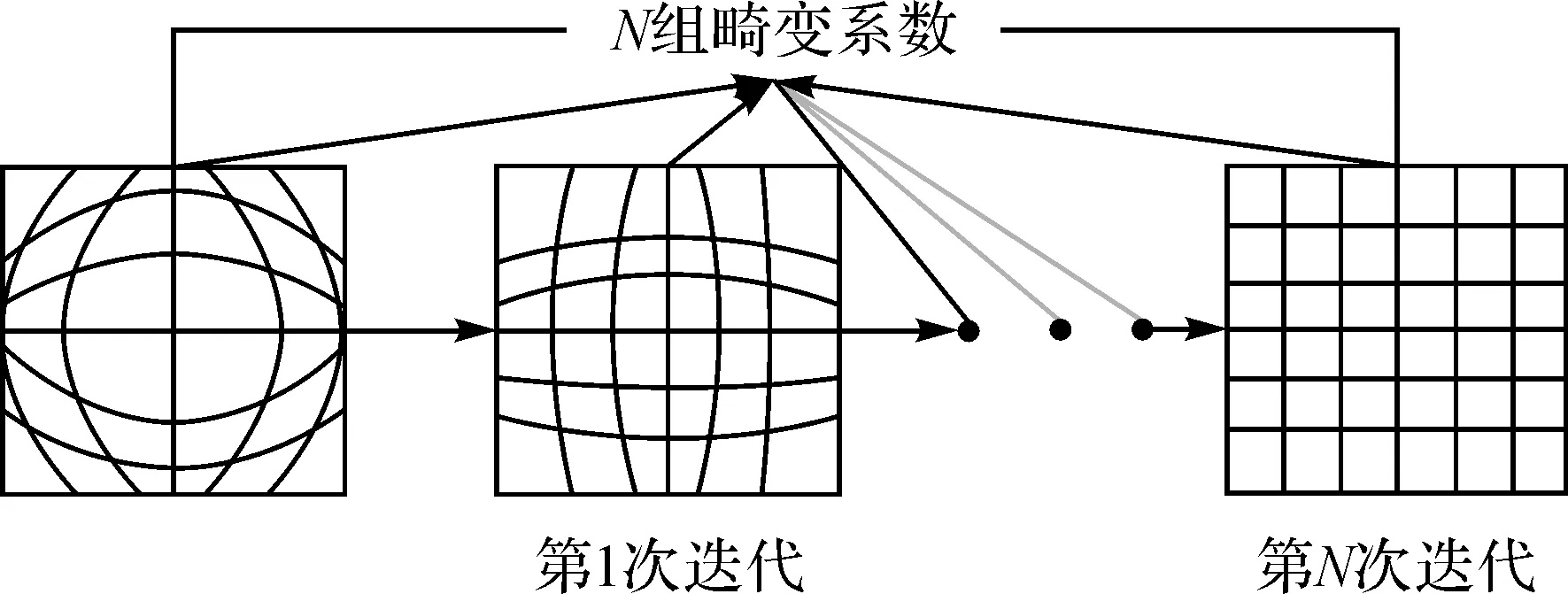
图2 相机迭代检校法原理示意图
用被检校的相机对简易检校场获取多景影像,在获取的多景影像上量测控制点对应的像点坐标,利用相机检校模型计算出影像外方位元素及相机内方位元素和畸变系数,利用这些系数对影像进行第一次畸变校正(常规检校法)。单次校正后影像一般仍有畸变存在,因此对校正后的影像进行迭代处理。将第一次校正后的影像作为初始影像,重新量测控制点的像点坐标,为了减少人工量测所有控制点的工作量,将第二次初始影像与第一次初始影像采用影像匹配(转刺控制点)。利用新的控制点影像坐标重新计算畸变系数,进行像畸变校正。依次类推,直至畸变变化小于预先设定的阈值,终止迭代,完成相机检校。相机迭代检校法的工作流程如图3所示。
2 试验与结果分析
本文选择了两种非量测相机进行了试验,相机A为佳能5DSr全幅单反相机,采用24 mm移轴定焦镜头,传感器尺寸为36 mm×24 mm,影像分辨率为8688×5792。相机B为富士双镜头立体3D相机W3,相机镜头是等效焦距,传感器尺寸为1/2.3英寸,影像分辨率为3648×2736。相机A与相机B均在6个与墙垂直距离近似相等的摄站点拍摄影像,每个摄站点之间水平距离大约在10~30 cm之间,共拍摄18景影像。相机B为双目立体视觉相机,共有左右两个相对水平距离约为7.5 cm、参数一致的镜头,本文主要对左镜头的6景影像进行检校。分别使用佳能相机和富士相机处理软件将影像转为TIFF格式,然后对影像进行坐标量测。为了专注对常规检校法和迭代检校法的比较和简化模型比较,本文暂不引入对主距的校正,但原则上迭代检校法同样适用于带主距校正的检校模型。
2.1 常规检校法与迭代检校法的相机检校试验分析比较
本文利用常规检校法和迭代检校法分别对相机A和相机B进行了多次试验,并对试验结果进行对比分析。试验一采用七号模型,使用常规检校法获取第一组畸变系数,使用迭代检校法获取共6组畸变系数。试验中相机A和相机B分别选取56个点和86个点计算空间坐标中误差(根据控制点前方交会的三维坐标与控制点三维坐标之间的误差统计)。相机A和相机B的常规检校法和迭代检校法的影像畸变中误差及空间坐标中误差见表1和表2。由于常规检校法与迭代检校法第一次迭代检校的结果一致,因此表中的迭代检校法只给出从第二次迭代的检校结果。
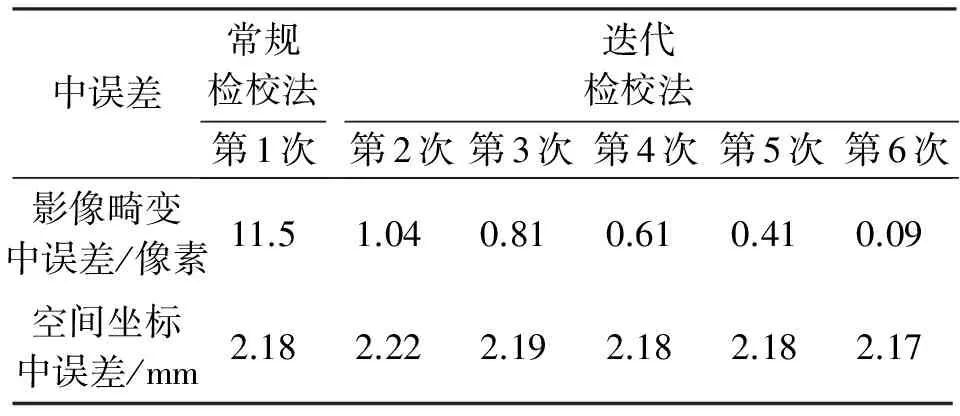
表1 相机A常规检校法与迭代检校法的误差分析

表2 相机B常规检校法与迭代检校法的误差分析
从表1、表2可以看出,常规检校法在经历了一次检校后仍然有畸变存在,迭代检校法能够通过多次迭代把畸变进一步减小。经过多次迭代,相机的畸变系数趋近于0(0.09像素)。而空间坐标中误差在几次迭代过程中相当稳定,几乎不变,合理的解释可能为控制点空间坐标的量测为2 mm(参考全站仪),而相机检校受到检校模型检校极限的影响,控制点影像坐标量测误差(相机分辨率等因素)和其他外界因素的影响,空间坐标中误差无法进一步提高。表1显示相机A的控制点中误差达到2.18 mm,表2显示相机B的空间坐标中误差达到11 mm,这可能是由于相机A作为全幅面成像及镜头质量远高于相机B所致,而通过迭代检校法相机B的空间坐标中误差稍有提高。
2.2 单模型迭代检校法与多模型组合迭代检校法的相机检校试验分析比较
迭代检校法的一个优点是可以灵活选用相机检校模型,即在整个迭代过程中既可以选用同一个检校模型,也可以适用不同检校模型进行组合迭代。本试验使用相机B的6张影像数据,分别采用五号模型的单一模型迭代法,与二号模型和三号模型交替迭代的迭代法进行检校。选用二号模型和三号模型交替迭代的另一层含义是五号模型的5个系数正好是三号模型的3个系数和二号模型的2个系数。二号模型和三号模型交替迭代的具体步骤为:第一次迭代选用三号模型,第二次迭代选用二号模型,依次类推,交替选用,直至满足相机检校需求。五号模型迭代及二号模型和三号模型交替迭代的影像畸变中误差和空间坐标中误差见表3。

表3 五号模型迭代检校法与二号模型和三号模型组合迭代检校法的误差分析
根据表3所示,二号模型与三号模型交替迭代的影像畸变中误差逐渐减小,最后趋近于0(0.06像素),而迭代法的空间坐标中误差也比常规法提高了约35%精度。选用单一模型(五号模型)的迭代法的影像畸变中误差在逐渐减小,最后趋近于0(0.02像素)。空间坐标中误差略有增大,可能受到控制点影像点位量测精度的影响。此试验结果表明,选用合理的多模型交替迭代可以达到选用单一模型迭代检校的效果。
2.3 有控制点迭代检校法与无控制点迭代检校法对比
为了拓宽提出的相机迭代检校法的应用面,本文在无控制点情况下进行了迭代法的研究。通过增加约束条件可解决无控制点情况下自由网平差法的方程系数阵秩亏问题从而到达收敛求解。同样按照本文提出的相机检校迭代处理的思路实现无控制点的相机迭代检校。在此把相机检校模型系数作为自由网的自检校系数进行求解。
把七号模型(Australis模型)作为自检检校模型分别对相机A和相机B进行无控制点迭代法试验。试验使用与上述试验相同的影像,无控制点迭代检校法与有控制点迭代检校法唯一不同的是把所有控制点作为检查点,把检查点的空间坐标作为未知数,只在最后把前方交会求得的检查点的空间坐标通过三维平移旋转缩放与检查点的量测坐标进行误差比较。试验对相机A分别进行6次迭代检校(在有控制点情况下)和5次迭代检校(在无控制点情况下);对相机B分别进行4次迭代检校(在有控制点情况下)和7次迭代检校(在无控制点情况下)。相机A和B的影像畸变中误差和空间坐标中误差见表4和表5。

表4 相机A有控制点与无控制点迭代检校法的误差分析

表5 相机B有控制点与无控制点迭代检校法的误差分析
根据表4、表5所示,相机A与相机B的无控制点迭代检校法的影像畸变中误差和空间坐标中误差整体均呈现减小趋势,但是两类误差都比有控制点迭代检校法的误差大(大约为2倍)。此试验表明无控制点迭代检校法的检校精度要差于有控制点迭代检校法的检校精度,此现象是否具有普遍性还有待进一步研究证实。
3 结论和展望
非量测相机的检校是摄影测量特别是摄影测量工业应用的关键环节之一。本文通过介绍构建简易快速的控制点检校场,为非量测相机的检校提供了一条便利的途径。首次提出了相机检校的迭代处理思路,即迭代检校法,详细介绍了有控制点和无控制点迭代检校法的处理流程,并且通过对两种相机一系列试验,对影像畸变精度和空间坐标精度进行了分析。试验结果表明,迭代检校法比常规检校法可以进一步提高相机检校的精度;迭代检校法可以另外选用单一或不同检校模型组合进行迭代检校,以适应不同相机和环境的检校;迭代检校法也可在无控制点的极端检校环境下应用,才可以达到与有控制点迭代检校相近的精度。本文试验也揭示,佳能全幅面单反相机(24 mm移轴定焦镜头)的影像畸变明显小于较廉价的富士立体相机W3。
进一步的工作包括研究引入对主距的校正,不同检校模型组合的迭代检校法对相机检校的效果及如何进一步提高无控制点迭代法的检校精度,使得迭代检校法能在更广阔的复杂环境中得到应用。
参考文献:
[1] 卫征,方俊永,张兵.非量测相机镜头光学畸变的改正[J].光学技术,2007(6):885-888.
[2] ZHAO S,LI X J,LIU T,et al.Camera Self-calibration Method Based on Large Scale Aerial Images Coplanarity Constraint[J].Acta Geodaetica et Cartographica Sinica,2017,46(1):98-106.
[3] 赵爽,李学军,刘涛,等.基于大比例尺航空影像共面约束条件的相机自检校方法[J].测绘学报,2017,46(6):98-106.
[4] ABDEL-AZIZ Y I,KARARA H M.Direct Linear Transformation from Comparator Coordinates into Object Space Coordinates in Close-range Photogrammetry[J].Photogrammetric Engineering and Remote Sensing,2015,81(2):103-107.
[5] 张永军,张祖勋,张剑清.利用二维DLT及光束法平差进行数字摄像机标定[J].武汉大学学报(信息科学版),2002,27(6):566-571.
[6] 吴军,徐刚,董增来,等.引入灭点约束的TSAI两步法相机标定改进研究[J].武汉大学学报(信息科学版),2012,37(1):17-21.
[7] 袁枫,张继贤,齐维君,等.非量测数字相机实验室几何标定[J].测绘学报,2016,45(5):601-607.
[8] 杨韫澜,胡海彦.非量测型数码相机检校及量测精度分析[J].测绘通报,2017(S1):206-209.
[9] ZHANG Z Y.A Flexible New Technique for Camera Calibration[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2000,22(11):1330-1334.
[10] 马颂德,张正友.计算机视觉——计算理论与算法基础[M].北京:科学出版社,1998.
[11] 王凤艳,黄润秋,陈剑平,等.基于计算机视觉和测量平差理论的相机标定[J].吉林大学学报,2017,47(3):944-951.
[12] FRASER C.Digital Camera Self-calibration[J].ISPRS Journal of Photogrammetry and Remote Sensing,1997,52(4):149-159.
[13] 张本昀,吴晓明,喻铮铮,等.非量测相机检校及可靠性研究[J].测绘科学,2008,33(5):84-86.
[14] 冯文灏.近景摄影测量[M].武汉:武汉大学出版社,2002.
[15] 李天子,郭辉.非量测数码相机的影像纠正[J].测绘通报,2006(10):59-61.

