等熵Chaplygin气体动力学系统三片常数的黎曼问题

周 同，杜珍珍，杨汉春

（1.铜陵职业技术学院基础教学部，安徽铜陵244000；2.云南大学数学与统计学院，云南昆明650091）

考虑等熵Chaplygin气体动力学系统，1904年，Chaplygin[1]首次引入了以下方程组：

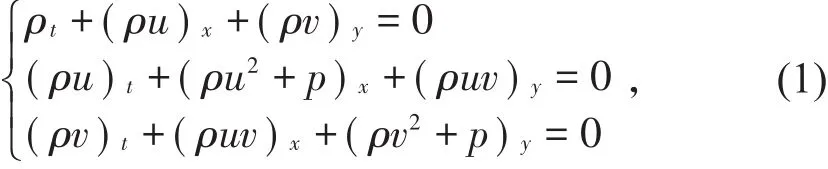
其中p=-1 ρ。在空气动力学中，当计算飞机机翼上升所承受的压力时，Tsien[2]和von Karman[3]把系统(1)作为一个合适的数学模型，(1)式还可以被视为暗物质和暗能量的统一模型[4-8]，而此暗能量模型对宇宙结构的形成有很大的影响。

对于一维情形Chaplygin气体的欧拉系统正是Born-Infeld[9]系统，它也是Maxwell系统的一个非线性形式。对于Chaplygin气体，Brenier[10]研究了一维黎曼问题并获得了初值在相平面上位于某特定区域时带有集中的解。

Serre[11]考虑了二维等熵无旋Chaplygin气体压力波的相互作用，证明了超音速解的存在性。最近，Guo等[12]系统地研究了等熵Chaplygin气体的一维和二维黎曼问题，构造了14种不同的黎曼解结构，且在一些情形中出现了δ-激波和简单波。特别地，对于系统(2)带有初值

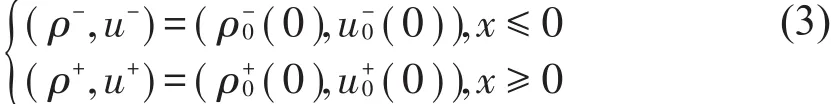
t=0:(ρ,u)(0,x)=的一维黎曼问题，解中一个显著的特征是出现了δ-激波。从物理角度上讲，δ-激波的形成是由于粒子的高度集中。δ-激波由波的位置、传播的速度和权（集中粒子的质量）决定。因此，δ-激波可用来解释宇宙中大尺寸结构星系的形成过程或粒子的集中过程。

本文考虑系统(2)带有以下3片常值

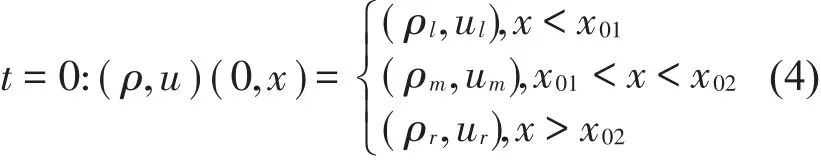
的黎曼问题，这里ρi,ui(i=l,m,r)是常数，x01,x02是x轴上任意的固定点。关于3片常数的黎曼问题很多学者进行过研究[13-15]。(2)式和(4)式黎曼问题的研究在狄拉克激波的理论、数值计算和应用等方面具有重要意义，它也是数值方法的检验标准。本文主要研究δ−激波和接触间断的相互作用。

当考虑光滑解时，可将系统(2)改写为

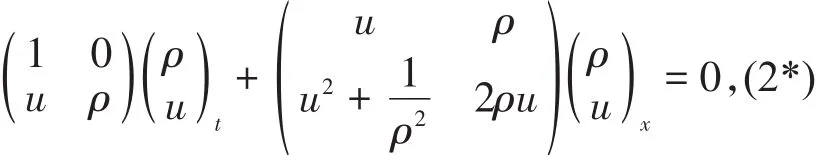
它的两个特征根和所对应的右特征向量分别是

且△λ±·r→±≡0，这表明，系统(2)是一个严格的线性退化的双曲系统。

对系统(2)求自相似解可知，除了常态解(ρ0,u0)外，该系统还有奇异解

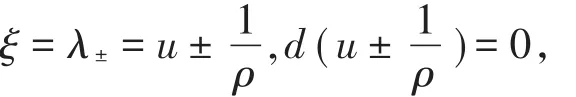
而对有界间断解，它仅有接触间断：σ=λ±=u±且这两种间断解曲线分别为

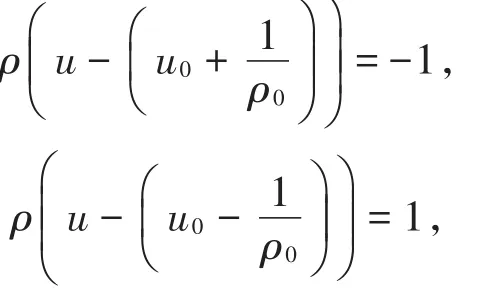
通过相平面分析法，文献[12]把相平面分成5个部分，对任意给定的(u+,ρ+)，完整地解决了黎曼问题(2)和(3)，得到5种不同的解的结构，如图1所示。

(1)当(u+,ρ+)∈ I(u-,ρ-)时，解为R←+R→；

(2)(u+,ρ+)∈ II(u-,ρ-)时，解为R←+S→；

(3)当(u+,ρ+)∈ III(u-,ρ-)时，解为S←+R→；

(4)当(u+,ρ+)∈ IV(u-,ρ-)时，解为S←+S→；

(5)当(u+,ρ+)∈ V(u-,ρ-)时，解为δ-激波。

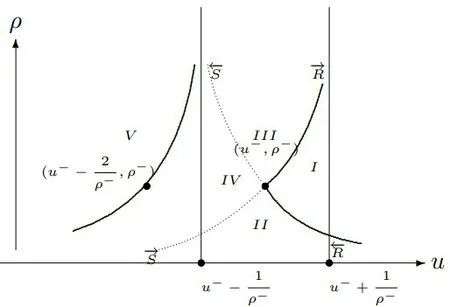
图1 解的相平面分析

对于前4种情况，能得到中间状态，它连接两种接触间断。对于情形(5)，δ−激波解具有如下形式：

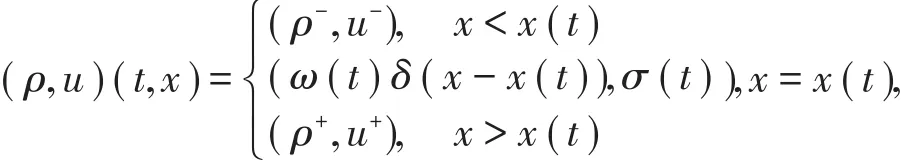
其中，x=x(t)为间断线，δ(x)是标准的狄拉克函数，ω(t)和σ分别为δ−激波的权和速度。其中x(t),ω(t)和σ(t)由下面方程组决定，其中，[ρ]= ρ-- ρ+,ρ-= ρ(σ-0),ρ+= ρ(σ +0)。(5)式中3个方程分别表示运动方程、质量守恒和动量守恒方程，它们描述了δ−激波的位置x=x(t)、传播速度σ(t)和权ω(t)之间的关系。(6)式表明δ−激波两边所有的特征线都是进入的。

当考虑初值带有狄拉克测度这类黎曼问题时，即对于一般情况，δ−激波从带有下列初值中产生：

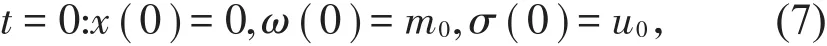
且满足

解初值问题(5)和(7)可得

引 理 2 若 (um,ρm)∈ V(ul,ρl) 且 (ur,ρr)∈V(um,ρm)，则有(ur,ρr)∈ V(ul,ρl)。

下面构造(2)式和(4)式的黎曼解。根据(u+,ρ+)在(u-,ρ-)所在区域，分情况讨论涉及δ−激波解的相互作用情况。

情形1(um,ρm)∈ V(ul,ρl)且(ur,ρr)∈V(um,ρm)。

图2 两个δ-激波相碰

如图2所示，当(um,ρm)∈ V(ul,ρl)且(ur,ρr)∈V(um,ρm)时，由前文可知，从初始间断(x01,0)和(x02,0)处分别发出δ1−激波和δ2−激波。由于这两个δ−激波都满足熵条件，有ul-，这表明δ1的传播速度σ1比δ2的传播速度σ2大。因此，δ1和 δ2在有限的时间处发生碰撞。此时，由于个新的黎曼问题将会形成，解一个新的δ−激波x=x(t)，其速度σ(t)和权ω(t)满足：

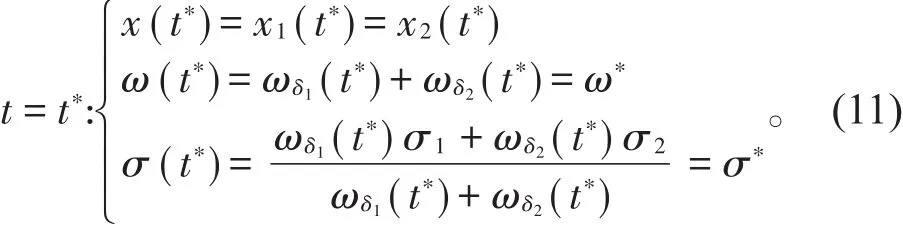
这是由于在t=t∗处满足质量守恒和动量守恒，通过计算可知σ1＞σ∗＞σ2。与前面相似，解常微分方程(5)和(11)式可获得δ−激波x=x(t)的轨迹、质量和速度：

当ρr≠ ρl时，

因此，在条件 (um,ρm)∈ V(ul,ρl)且 (ur,ρr)∈V(um,ρm)下，由引理1得到的结论是两个δ−激波必在有限的时间内发生碰撞，它们结合后产生一个新的δ−激波，这个事实表达为δδ→δ。

情形 2 (um,ρm)∈ V(ul,ρl)且(ur,ρr)∈III(um,ρm)。当 (um,ρm)∈ III(ul,ρl)且 (ur,ρr)∈ V(um,ρm)时，解的构造类似。

此种情况，由于(um,ρm)∈ V(ul,ρl)，从初始间断 (x01,0)发出 δ1−激波。由 (ur,ρr)∈ III(um,ρm)知，从初始间断(x02,0)发出接触间断和，以及由确定(u∗,ρ∗)状态。

由于δ1−激波满足熵条件，有接触间断满其中τ1为接触间断的速度，接触间断满足τ2=为接触间断的速度。

σ1,τ1,τ2的速度可能为正，也可能为负，分为以下几种情况：（1）σ1＞ 0,τ1＜ 0,τ2＞ 0；（2）σ1＞ 0,τ1＞0,τ2＞ 0 ，（3）σ1＞ 0,τ1＜ 0,τ2＜ 0 ；（4）σ1＜ 0,τ1＜0,τ2＞ 0 ；（5）σ1＜ 0,τ1＞ 0,τ2＞ 0 ；（6）σ1＜ 0,τ1＜0,τ2＜ 0。本文只讨论情况（1），其他情况类似。

如图3所示，由于σ1＞ τ1，所以δ1−激波的传播速度比接触间断的速度大，因此，δ1和←S在有限的时间处发生碰撞。通过计算比较可知所以δ1和在t1相碰后，一个新的黎曼问题产生，解一个新的δ−激波x=x(t)，其速度ω(t)和权σ(t)满足

这是由于在t=t1处满足质量守恒和动量守恒。解常微分方程(5)和(12)式可获得δ2−激波的轨迹、质量和速度(x2(t),ω2(t),σ2(t))。

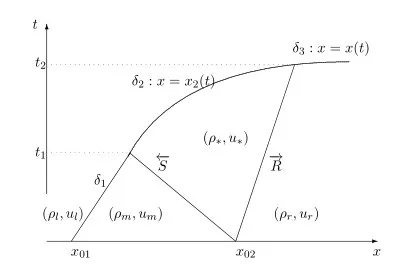
图3 δ-激波与接触间断和R相碰

因为δ的传播速度σ满足熵条件可知σ ＞ τ ，所以δ和在有限的222时间t2处发生碰撞，且有x2(t2)=τ2t2+x02。因为故δ和2在t2相碰后，一个新的黎曼问题产生，解一个新的δ−激波x=x(t)，其速度ω(t)和权σ(t)满足：这是由于在t=t2处满足质量守恒和动量守恒。解常微分方程(5)和(13)式可获得δ3−激波的轨迹，质量和速度(x(t),ω(t),σ(t))。

因此，在条件 (um,ρm)∈ V(ul,ρl)且 (ur,ρr)∈III(um,ρm)下，由引理1得δ−激波和两个接触间断相碰，当相互作用完成后，完全赶超中间状态(u∗,ρ∗)，其中(u∗,ρ∗)连接两个接触间断和，这

情 形 3 (um,ρm)∈ V(ul,ρl) 且 (ur,ρr)∈ IV(um,ρm) 。 当 (um,ρm)∈ IV(ul,ρl) 且 (ur,ρr)∈V(um,ρm)时，解的构造类似。

此种情况，由于(um,ρm)∈ V(ul,ρl)，从初始间断 (x01,0)发出 δ1−激波。由 (ur,ρr)∈ IV(um,ρm)知，从初始间断(x02,0)发出接触间断S←和S→，以及由S←和S→确定(u∗,ρ∗)状态。

由于接触间断→S与情形2中接触间断R→的表达式一样，故此种情形与情形2讨论类似。

因 此 ，在 条 件 (um,ρm)∈ V(ul,ρl)且(ur,ρr)∈IV(um,ρm)下，由引理1得δ−激波和两个接触间断和相碰后，完全赶超中间状态(u∗,ρ∗)，其中(u∗,ρ∗)连接两个接触间断和，这个事实表达为δ←S(u∗,ρ∗)→S→ δ。

情 形 4 (um,ρm)∈ V(ul,ρl) 且 (ur,ρr)∈II(um,ρm) 。 当 (um,ρm)∈ II(ul,ρl) 且 (ur,ρr)∈V(um,ρm)时，解的构造类似。

此种情况，由于(um,ρm)∈ V(ul,ρl)，从初始间断(x01,0)发出δ1−激波。由(ur,ρr)∈ II(um,ρm)知，从初始间断(x02,0)发出接触间断R←和→S，以及由和确定(u∗,ρ∗)状态。

由于δ1−激波满足熵条件，有，接触间断满足其中τ1为接触间断的速度，接触间断满足τ2=其中τ2为接触间断的速度。

由于σ1,τ1,τ2的速度可能为正也可能为负，与情形2类似，可分为6种情况，在这里只讨论第1种情况：σ1＞ 0,τ1＜ 0,τ2＞ 0，其他情形可类似讨论。

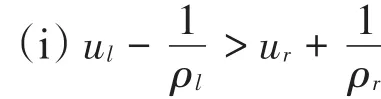
由于σ1＞ τ1，所以δ1−激波的传播速度比接触间断 R←的速度大，因此，δ和 R←在有限的时间处发生碰撞，如图4所示。

图4 δ-激波与接触间断和相碰

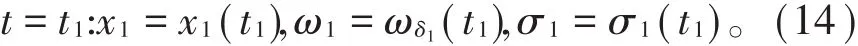
这是由于在t=t1处满足质量守恒和动量守恒。解常微分方程(5)和(14)式可获得δ2−激波的轨迹、质量和速度(x2(t),ω2(t),σ2(t))。

因为δ2的传播速度σ2满足熵条件可知σ2＞ τ2，所以δ2和在有限的时间t2处发生碰撞，且有x2(t2)=τ2t2+x02。因为故δ和2在t2相碰后，一个新的黎曼问题产生，解一个新的δ−激波x=x(t)，其速度ω(t)和权σ (t)满足：

这是由于在t=t2处满足质量守恒和动量守恒。解常微分方程(5)和(15)式可获得δ3−激波的轨迹、质量和速度(x(t),ω(t),σ(t))。

此时，由引理1得δ−激波和两个接触间断R←和→S 发生碰撞且完全赶超中间状态(u,ρ)，其中

∗∗这个事实表达

与（i）情形类似，如图5所示，δ1−激波首先与发生碰撞，形成一个新的δ2−激波并开始赶超(u∗,ρ∗)状态。通过分析知 δ−激波不能完全赶超(u∗,ρ∗)状态，这个事实表达为 δ(u∗,ρ∗)→δ(u∗,ρ∗)

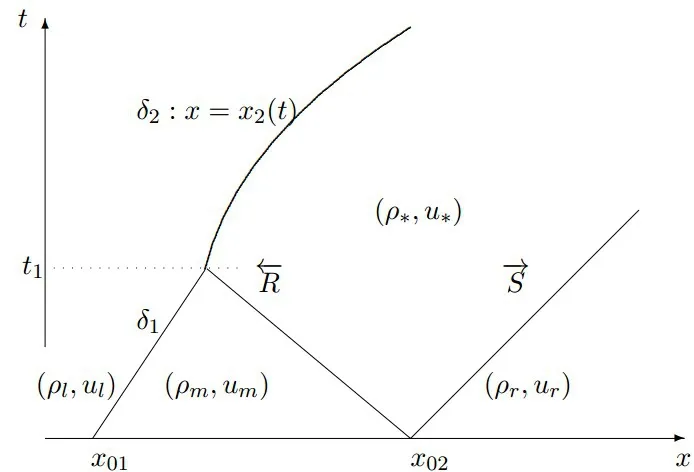
图5 δ-激波与接触间断和相碰

情 形 5 (um,ρm)∈ V(ul,ρl) 且 (ur,ρr)∈I(um,ρm) 。 当 (um,ρm)∈ I(ul,ρl) 且 (ur,ρr)∈V(um,ρm)时，解的构造类似。

此种情况，由于(um,ρm)∈ V(ul,ρl)，从初始间断(x01,0)发出δ1−激波。由(ur,ρr)∈ I(um,ρm)知，从初始间断(x02,0)发出接触间断，以及由确定(u∗,ρ∗)状态。

由于接触间断与情形4中接触间断的表达式一样，故此种情形与情形4讨论类似。

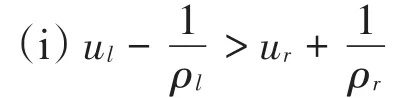
此时，由引理1得δ1−激波和两个接触间断发生碰撞且完全赶超中间状态(u,ρ)，其

∗∗中(u∗,ρ∗)连接两个接触间断，这个事实表达为

此时，δ−激波不能完全赶超(u∗,ρ∗)状态，这个事实表达为δ

[1]CHAPLYGIN S.On gas jets[J].Sci Mem Moscow Univ Math Phys,1904,21:1-121.

[2]TSIEN H S.Two dimensional subsonic flow of compressible fluids[J].JAeron Sci，1939,6:399-407.

[3]KARMAN T VON.Compressibility effects in aerodynamics[J].JAeron Sci,1941,8:337-365.

[4]BILIC N,TUPPER G B,VIOLLIER R.Dark matter,dark energy and the Chaplygin gas[J].Dark Matter in Astro-&Particle Physics,2002,535:306-311.

[5]CRUZ N,LEPE S,PENA F.Dissipative generalized Chaplygin gas as phantom dark energy Physics[J].Phys Lett B,2007,646:177-182.

[6]PASQUIER V,MOSCHELLA U,GORINI V,et al.The Chaplygin gas as a model for dark energy[J].The Tenth Marcel Grossmann Meeting:On Recent Developments in Theoretical and Experimental General Relativity,Gravitation and Relativistic Field Theories,2006,3:840-859.

[7]SETARE M R.Holographic Chaplygin gas model[J].Phys Lett B,2007,648:329-332.

[8]SETARE M R.Interacting holographic generalized Chaplygin gas model[J].Phys Lett B,2007,654:1-6.

[9]BORN M,INFELD L.Foundations of the new field theory[J].Proc Roy Soc London,1934,A(144):425-451.

[10]BRENIER Y.Solutions with concentration to the Riemann problem for one-dimensional Chaplygin gas equations[J].J Math Fluid Mech,2005,7:S326-S331.

[11]SERRE D.Multidimensional shock interaction for a Chaplygin gas[J].Arch Rational MechAnal,2009,191:539-577.

[12]GUO L H,SHENG W C,ZHANG T.The two-dimensional Riemann problem for isentropic[J].Chaplygin gas dynamic system,2010,9:431-458.

[13]CHENG H J,YANG H C.Two-dimensional Riemann problems for zero-pressure gas dynamics with three constant states[J].J MathAnalAppl,2008(343):127-140.

[14]GU Y L,TONG Y C,YANG H C.The Riemann problem with three constants for steadyzero-pressure isentropic flown[J].Journal of Kunming Teachers College,2007,29(4):10-15.

[15]YANG H C，Hu R,SUN Y.The Riemann problem with three constant initial states for one-dimensional zero-pressure gas dynamics[J].Southeast Asian Bulletin of Mathematics,2009,33:179-187.