设疑、析疑、新知、应用
——例谈学案导学模式下的课堂教学
孔祥明
(南京市金陵汇淳学校,江苏 南京)
所谓学案导学是把课堂的流程用文本的形式固化下来,让学生按学案的指引完成一节课的学习,相对于传统课堂教学,它使课堂在预设的框架下运行,有效地防止了课堂的随意性,确保了课堂教学的效果,但也有教师认为学生要兼顾教师的讲解与学案的完成,常使课堂不流畅,气氛不活跃,甚至觉得禁锢了学生的思维,其实这些老师的问题在于对学案导学认识不足,继而学案编写不切合实际,没有抓住学案导学的关键。本文就苏科版八上“6.3.一次函数的图象”第一课时为例,谈谈学案导学模式下的课堂教学.
一、设疑
学案导学环节一:课前导疑
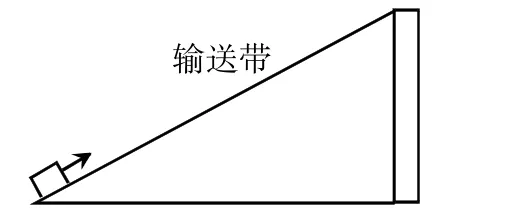
问题:输送带从地面传送货物.如图,输送带每分钟高度上升2米,设时间为 x(分钟),高度为 y(米).
①填表

x__(分钟) 0 1 2 3 4 …y___(米) 0 …
②写出高度y(米)与时间x(分)之间的函数关系式;
③你能用图象法表示这个函数关系吗?
【设计意图】疑是学之始,每节课设置一个与本节课相关的问题,问题不在多、难,重在启发思考,本题隐含函数的三种表示方法,输送带动态的过程给了学生高度随着时间的改变而改变的想象空间,而且输送带的直线形状也让学生对一次函数图象是一条直线有了初步的感知.这个背景具有“动态”和“直线”两个一次函数的典型特征,学生也容易接受.
二、析疑
学案导学环节二:课前问题分析,明确问题指向
解决上述问题你有什么困难?
【设计意图】通过对问题的分析,明确问题中什么能够解决,什么是要去学习的,新的问题的必要性是什么。本题中表格只能部分反映变化过程,关系式不直观,更是一种描述,而函数的图象更能直观地表现连续变化的过程,进而明确本节课的任务就是画一次函数的图象.
三、新知
学案导学环节三:课堂活动
活动一:1.怎样画函数y=2x的图象呢?它是什么形状?
2.怎样画函数y=2x+1的图象呢?它是什么形状?
【设计意图】通过这个活动,学生在平面直角坐标系中,根据上文中的表格,画出图象.这个过程其实就经历了看列表、描点、画线三个步骤,并感受一次函数的图象是一条直线.
活动二:1.既然一次函数的图象是一条直线,你能用更简单的方法画一次函数y=-3x+3的图象吗?(例题教学)
2.点A(1,3)在这个函数图象上吗?你是怎样判断的?
3.你怎样理解画一次函数图象的三个步骤?
【设计意图】第1问总结一次函数图象的画法.这个问题同时也作为一道例题.第2问让学生思考可以从形上发现点A不在函数图象上,也可从数的角度,把点A的坐标代入y=-3x+3,发现不满足函数关系式,所以点A不在函数图象上,进而使学生感知符合关系式的点就在函数图象上,反之在函数图象上所有点的坐标都满足函数关系式.第3问紧扣函数的定义,让学生更深层次理解画函数图象的一般方法.这里,每一个探索活动都建立在上一探索活动的基础上,不断上升,使学生对函数及函数图象的理解不断上一新的台阶.
四、应用
学案导学环节四:练习
画y=2x+1、y=2x-1的图象.
五、课堂小结
学案导学环节五:小结
说说你对直线有什么新的认识.
【设计意图】设计简练的小问题对课堂进行小结,一定要抓住问题本质,直线是一种“形”,但在直角坐标系中,它又是一个函数的图象,它就是“数”,值得学生细细品味.
学案导学的课堂教学模式不同于教案,它更像学生的一张学习操作单,学案的核心在于指导学生学习,要在导学上下功夫,学案的主体是学生活动,要根据教学目标,以问题(串)、追问等方式引导学生经历知识的发生、发展过程,并将所学知识融入学科知识体系中,尽量让学生体会知识的必要性,理清知识的来龙去脉,避免死记硬背.学生活动不能过多,问题不能琐碎,要留足学生的活动空间,充分调动学生思维,让学习真正发生.
在实施教学时,要充分认识学案的导向作用,要留出足够的阅读时间给学生,学案上有的且表述清楚的老师就不要赘述,避免重复获取信息造成时间浪费,要充分利用学案培养学生的文本阅读能力。要完全转变教学中教师一言堂的做法,要时刻关注学生的解答情况,充分发挥学习小组的作用,对每个教学环节要说得清、完得成.
在学案编制的过程中,要注意整合各方的资源,在一张学案上要整合教材、课件、作业等内容,甚至可以把学案设计成课堂笔记的式样,让课堂场景留下痕迹,要注意给学生留下反思的空间,让思维也留痕,最大限度地发挥导学案的价值.

