第58届IMO平面几何题命题探秘

江苏省连云港市新海实验中学 (222200) 仇玉祥

人教版、苏教版普通高中课程标准实验教科书数学选修4-1《几何证明选讲》都选用了下列经典例题：

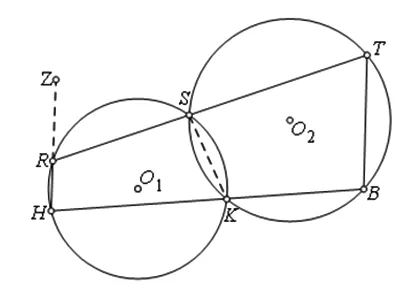
图1

原题如图1，⊙O1、⊙O2交于点S、K，直线RT过点S，与⊙O1、⊙O2分别交于点R、T，直线HB过点K，与⊙O1、⊙O2分交于点H、B，求证：RH∥TB．

延长HR到点Z，并连结SK，注意到∠ZRS=∠HKS=∠STB，即知RH∥TB．

下面，让我们来看看这道经典例题是如何被卢森堡数学奥林匹克命题专家巧妙演绎为国际数学奥林匹克(IMO)平面几何试题的.

1.极端化

如图1，记RH所在直线为l，令点H、B分别在⊙O1、⊙O2上运动(直线HB过点K)，当点H趋近于点R并最终与点R重合时，直线l由割线变为切线(切点为R)，显然有l∥TB，于是我们得到：

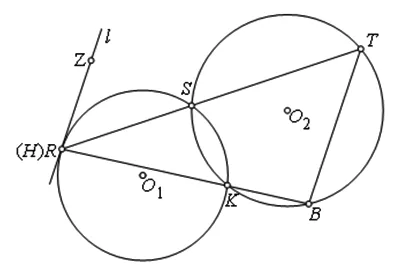
图2

命题1 如图2，⊙O1、⊙O2交于点S、K，直线l与⊙O1相切于点R，射线RS、RK与⊙O2分别交于点T、B，则l∥TB．

命题1是人教版原初中数学课本中的经典习题．

2.特殊化

如图2，令点R在⊙O1上运动，同时点T、B在⊙O2上运动(直线RT过点S，直线RB过点K)，到点S为线段RT的中点时运动停止，命题1显然成立．于是我们得到：

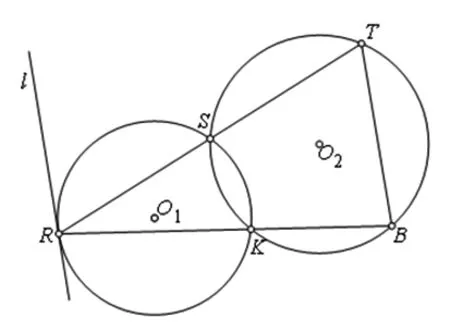
图3

命题2 如图3，⊙O1、⊙O2交于点S、K，直线RT过点S，与⊙O1、⊙O2分别交于点R、T(点S为线段RT的中点)，射线RK与⊙O2交于点B，直线l与⊙O1相切于点R，则l∥TB．

3.纵深化

如图4(在图3的基础上)，连结BS，并延长交直线l于点A，连结AT、AK、KT、SJ，设AK与⊙O1交于点J，注意到RA∥TB，知∠ARS=∠BTS，∠RAS=∠TBS，结合RS=TS，即知ΔRAS≌ΔTBS，从而知RA∥TB，故四边形RATB是平行四边形，于是ATRB．

注意到∠SJK=∠SRK=∠ATS，知A、J、S、T四点共圆，记此圆为⊙O3．再注意到

∠KTS=∠SBK=∠TAS，KT与⊙O3相切于点T．

4.构造赛题

在图4中，去掉⊙O2以及线段AT、AB、BT、RB，添加线段JT，并将⊙O1、⊙O3分别替换成Ω、Γ，即可构作2017年7月在巴西里约热内卢举办的第58届国际数学奥林匹克(IMO)第4道赛题：

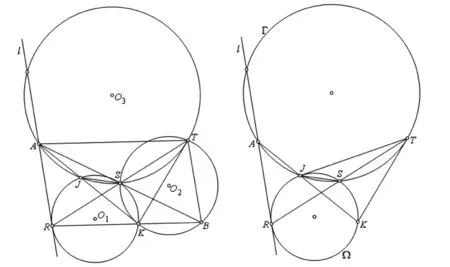
图4 图5

[1]第58届IMO试题[J].中等数学，2017，8.

[2]姚一隽．第58届IMO试题解答[J].中等数学，2017，9.