一个“新”的直线系
江西省樟树中学 (331200) 万浩春
(文)16.设直线系M:xcosθ+(y-2)sinθ=1(0≤θ≤2π),对于下列四个命题:
A.存在一个圆与所有的直线相交
B.存在一个圆与所有的直线不相交
C.存在一个圆与所有的直线相切
D.M中的直线所能围成的三角形面积都相等
其中真命题的代号是 (写出所有真命题的代号).
(理)16.设直线系M:xcosθ+(y-2)sinθ=1(0≤θ≤2π),对于下列四个命题:
A.M中所有直线均经过一个定点
B.存在定点P不在M中的任意一条直线上
C.对于任意整数n(n≥3),存在正n边形,其所有边均在M中的直线上
D.M中的直线所能围成的三角形面积都相等
其中真命题的代号是 (写出所有真命题的代号).
解决这两道题的关键在于读懂直线系M:xcosθ+(y-2)sinθ=1(0≤θ≤2π)是什么样的直线系?直线系中的直线拥有什么样的共同特征?
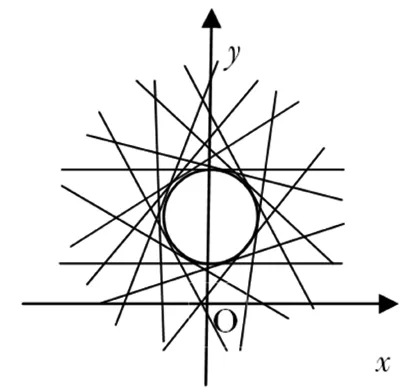
图1
我们观察方程xcosθ+(y-2)sinθ=1(0≤θ≤2π),可以发现定点(0,2)到方程表示的所有直线的距离均为1,那么这个方程表示的直线系就是以(0,2)为圆心,以1为半径的圆的所有切线组成的直线系.如图1所示
对于(文)16ABC这三个选项容易判断均正确,D选项不正确,因为M中的直线所能围成的三角形并不都是定圆的外切三角形,有时是三角形的边的延长线和定圆相切.对于(理)16,A显然不对,B、C正确,D不正确.
这个“新”的直线系不同于我们已经熟知的平行(或垂直)某一直线的直线系,或恒过某一定点的直线系,他是由一个定圆的所有切线组成的直线系.
那么对于任意一个圆,它的所有切线能组成一个直线系吗?如果能,这个直线系的方程是什么呢?
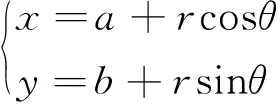
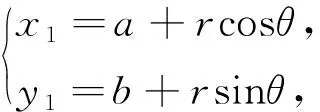
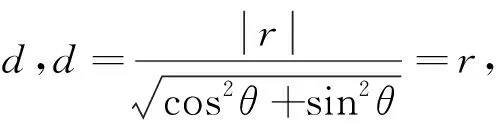

图2

一般地,圆(x-a)2+(y-b)2=r2的所有切线组成的直线系方程为(x-a)cosθ+(y-b)sinθ=r(0≤θ≤2π).
(特别说明,这个θ就是圆的参数方程中的参数,所以它的几何意义表示:以圆心为顶点,平行于x轴正方向的直线为始边,切点与圆心的连线为终边的角,如图2.)
利用这个“新”的直线系我们可以比较简单的解决下列问题
例1l1与l2是直线系M:(x+1)cosθ+(y-2)sinθ=3(0≤θ≤2π)中的两条平行线,则l1与l2间的距离为( ).

分析:直线系M:指的是以(-1,2)为圆心,3为半径的圆的所有切线,∵l1∥l2,又都与圆相切,∴l1与l2间的距离就是圆的直径,故选C.
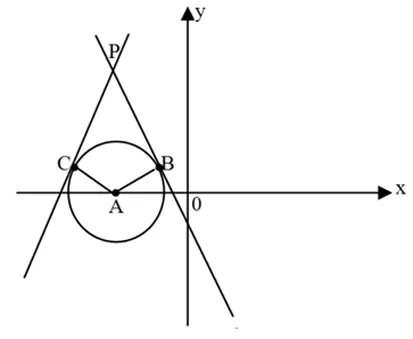
图3
例2l1:(x+3)cos25°+ysin25°=2,l2:-(x+3)sin55°+ysin35°=2,l1与l2相交于P点,则P到A(-3,0)的距离为 .
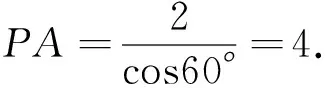
例3 在平面直角坐标系中既能用(x-1)cosθ+(y-2)sinθ=1表示又能用(x-3)cosθ+(y-1)sinθ=2表示的直线一共有几条?
分析:(x-1)cosθ+(y-2)sinθ=1表示以(1,2)为圆心,1为半径的圆的所有切线组成的直线系,(x-3)cosθ+(y-1)sinθ=2表示以(3,1)为圆心,2为半径的圆的所有切线组成的直线系.
故这道题的实质是求两圆(x-1)2+(y-2)2=1和(x-3)2+(y-1)2=4共有多少条公切线.
解:∵圆(x-1)2+(y-2)2=1和(x-3)2+(y-1)2=4相交,所以合题意的直线共有2条.
任意一个圆的所有切线能组成一个直线系,那么一个椭圆的所有切线能否组成一个直线系?这个直线系的方程该如何表示?
我们可以类比圆的切线系方程的推导过程进行推导.

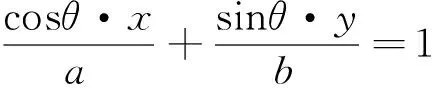

A.存在一个圆与所有的直线相交
B.存在一个圆与所有的直线不相交
C.存在一个圆与所有的直线相切
D.M中所有直线均经过一个定点
E.存在定点P不在M中的任意一条直线上
其中真命题的代号是 (写出所有真命题的代号).

例5 已知l1:3cos25°x+4sin25°y=12,l2:3sin54°x+4sin54°y=12,若两条直线交于点P,则点P( ).
A.在圆x2+y2=9的内部
B.在圆x2+y2=9的外部
C.在圆x2+y2=9上
D.无法判断与圆x2+y2=9的位置关系

封闭图形圆和椭圆都有切线系,那么另外的两个圆锥曲线双曲线和抛物线是不是也有类似切线系?
也就是说,只要把曲线的参数方程代入过曲线上某一点的切线方程,就可以得到曲线的所有切线组成的直线系方程.这为我们以后解决与圆锥曲线的切线有关问题提供了一个全新的思考途径.

