利用图像“顶天立地”解多元参数题
浙江省杭州高级中学 (310003) 王希年
我们知道,二次函数f(x)=ax2+bx+c(a≠0)的图像与函数y=ax2的图像形状相同,f(x)的图像相当于函数g(x)=ax2的图像经过平移而得到的.而函数y=ax2的图像可以看作对函数y=x2的图像进行了伸缩变换,抛物线的开口大小由|a|决定,|a|越大,开口越小.也可以把二次函数f(x)=ax2+bx+c的图像看成是y=ax2和y=bx+c图像的纵向叠加,也可以看成是y=ax2和y=-bx-c图像的纵向减损.
波利亚的“怎样解题表”将解题过程分成了四个步骤:第一,你必须弄清问题.第二,找出已知数与求知数之间的联系.第三,拟定、实行你的计划.第四,验算所得到的解,回顾反思.
在课堂教学中,我们用波利亚的四个步骤来讲题.下面通过一些例题及变式来讲清楚“顶天立地”的方法,以供教学参考.
一、利用图像平移,恰好“顶天立地”时,找问题解决方案
例1 设函数f(x)=|x2+ax+b|在[0,2]上的最大值为M,求M的最小值.
分析:1°函数y=x2+ax+b与y=x2的图像形状相同,函数y=x2+ax+b的图像相当于函数y=x2的图像经过平移而得到的.
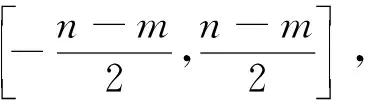
3°在对称轴右侧,函数y=x2递增,递增速度越来越快;在对称轴左侧,函数y=x2递减,递减速度越来越慢.因此,当函数g(x)=x2+ax+b的对称轴在区间[0,2]的中点时,g(x)max-g(x)min最小,即n-m最小.所以,当g(0)=g(2)=M,g(1)=-M.现把直线y=M叫做天线,把直线y=-M叫做地线,g(x)=x2+ax+b的图像“顶天立地”时,M取得最小值.
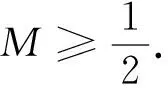
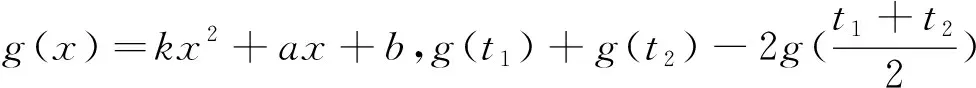
2°图像分析得出的解是不严密的,在分析好答案后,要严格给出代数推理并给于论证.

二、利用伸缩变换,恰好“顶天立地”时,找问题解决方案
例2 (2010年全国联赛一试)已知函数f(x)=ax3+bx2+cx+d(a≠0),当0≤x≤1时,|f′(x)|≤1,试求a的最大值.
分析:1°我们知道f′(x)=3ax2+2bx+c的图像与函数y=3ax2的图像形状相同,f′(x)的图像相当于函数g(x)=3ax2的图像经过平移而得到的,|3a|越大,抛物线的开口越小,函数g(x)=3ax2的图像可以看成是y=x2的图像经过伸缩变换而得到的.
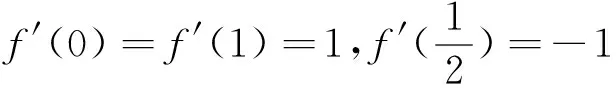
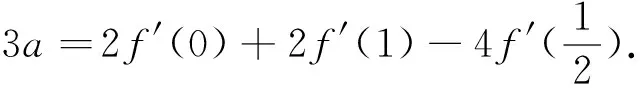
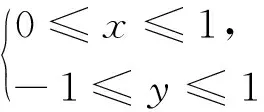
变式2 设函数f(x)=kx2+ax+b(k>0),记M为函数y=|f(x)|在[-1,1]上的最大值,N为|a|+|b|的最大值,若M=2k,求N.
分析:1°由文章开头所述,f(x)=kx2+ax+b(a,b∈R)的图像与函数y=kx2的图像形状相同,f(x)的图像相当于函数g(x)=kx2的图像经过平移而得到的.在对称轴右侧,函数g(x)=kx2递增,递增速度越来越快;在对称轴左侧,函数g(x)=kx2递减,递减速度越来越慢.
当长度为2的区间[t,t+2]在g(x)=kx2对称轴右侧时,t>0,g(x)max-g(x)min=g(t+2)-g(t)=4tk+4k>4k;当长度为2的区间[t,t+2]在g(x)=kx2对称轴左侧时,t<-2,g(x)max-g(x)min=g(t)-g(t+2)=-4tk-4k>4k;但当g(x)=kx2对称轴在[t,t+2]内时,-2≤t≤0,g(x)max-g(x)min=max{g(t),g(t+2)}-g(0)=max{g(t),g(t+2)}≤4k.
2°固定1°中长度为2的区间[t,t+2]为[-1,1],让函数g(x)=kx2平移成f(x)的图像,由1°知道,当区间在f(x)的对称轴的右边或左边时,f(x)max-f(x)min>4k,因此,f(x)max>2k和
f(x)min<-2k,一定有一个成立,否则f(x)max-
f(x)min≤4k.这样必有M>2k.
3°由1°和2°知,当a,b满足M≤2k时,f(x)的对称轴在区间[-1,1]内,回到原始情形,先把函数g(x)=kx2的图像左右平移|t|个单位,再向下平移-n个单位,得到y=k(x-t)2+n(-1≤t≤1,-2k≤n<0).即y=kx2-2tkx+kt2+n,当-1≤t≤0时,f(x)max=f(1)=k(1-t)2+n≤2k,即n≤2k-(1-t)2k对-1≤t≤0恒成立,则n≤-2k,又由-2k≤n<0,所以n=-2k.
同理,当0≤t≤1时,f(x)max=f(-1)=k(-1-t)2+n≤2k,即n≤2k-(1+t)2k对0≤t≤1恒成立,则n≤-2k,又由-2k≤n<0,所以n=-2k.此时y=k(x-t)2-2k(-1≤t≤1),|a|+|b|=2k|t|+k|t2-2|=-kt2+2k|t|+2k=-k(|t|-1)2+3k≤3k,当t=±1时,|a|+|b|取最大值3k.
反思:先确定f(x)的对称轴在区间[-1,1]内,|a|与左右平移量有关,|b|与上下平移量有关,从而猜想|a|+|b|取最大值时,对称轴靠边,并且{f(-1),f(1)}={-2k,2k}.
三、利用图像叠加,恰好“顶天立地”时,找问题解决方案
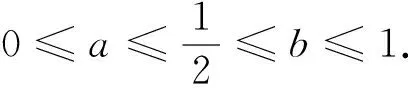
(1)证明:f(b)≤f(a);(2)设f(a)-f(b)≤M(a,b),求M(a,b)的最小值.
分析:分别画出y=2x和y=cosπx在[0,1]的图像,两图形叠加即为f(x)=2x+cosπx的图像,由描点可近似地画出f(x)的图像是有两个极值点的N形图像.
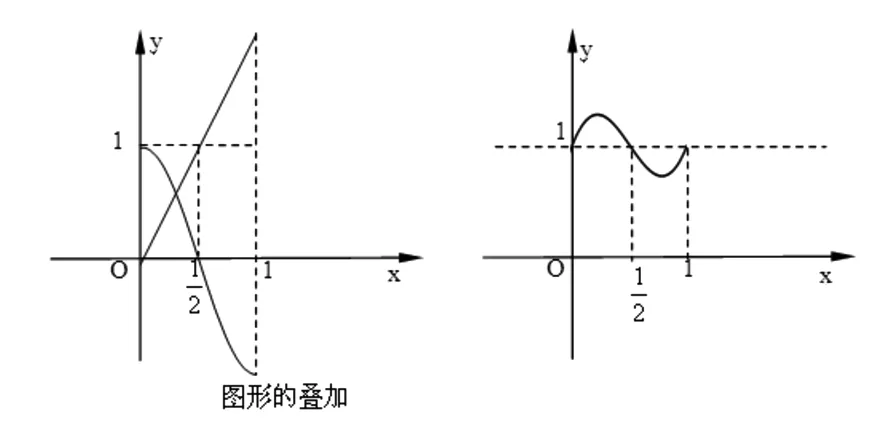
图1 图2
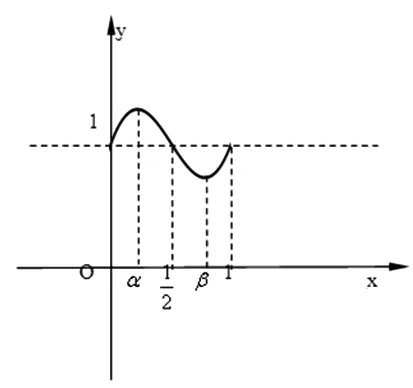
图3
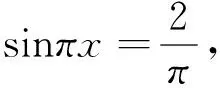
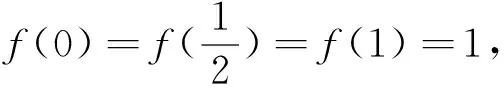
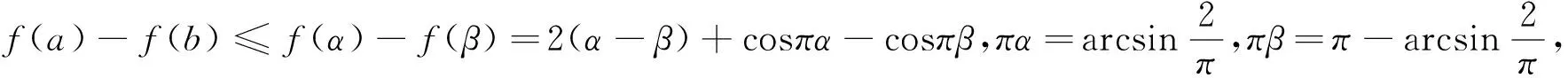
反思:运算过程中适当运用图形帮助理解,可以得到更清晰的解题思路,可以提高解题的正确率,所以,我们说数形结合中,数也离不开形.
变式3 已知f(x)=8x3+ax2+bx,是否存在实数a,b,使得对任意x∈[-1,1],均有|f(x)|≤2.若存在,求出a,b的值;若不存在,请说明理由.
分析:f(x)=8x3+ax2+bx的图像可以看成是函数y=8x3和g(x)=ax2+bx的图像叠加,y=8x3在[-1,1]上的值域为[-8,8],与g(x)=ax2+bx的图像叠加后,要使|f(x)|≤2成立,先考察两端,必须g(1)=a+b≤-6,g(-1)=a-b≥6,相减消去a得b≤-6,但当a>0时,f(1)=8+a+b≤2+a,|f(1)|≤2不一定成立;当a<0时,f(-1)=-8+a-b≥-2+a,|f(-1)|≤2不一定成立;
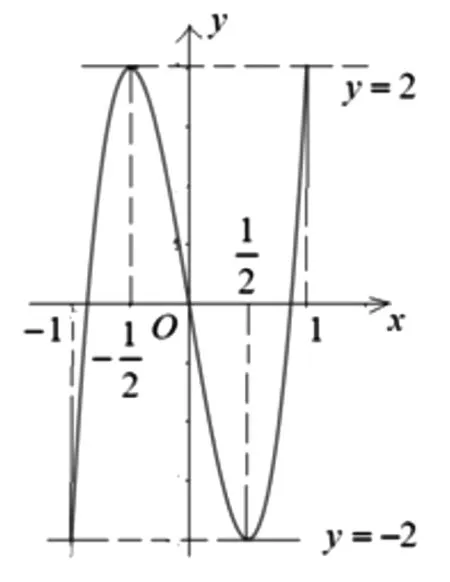
图4
画图叠加,当a≠0时,|f(x)|≤2不恒成立.
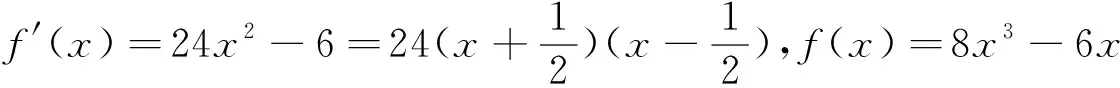
上图是函数y=8x3和g(x)=-6x的图像叠加所得,图像与直线y=2和直线y=-2“顶天立地”,若改变b的取值,就会改变这种极致情形,使得|f(x)|≤2不恒成立.所以存在a=0,b=-6,使得对任意x∈[-1,1],均有|f(x)|≤2.
解析:根据题意,有
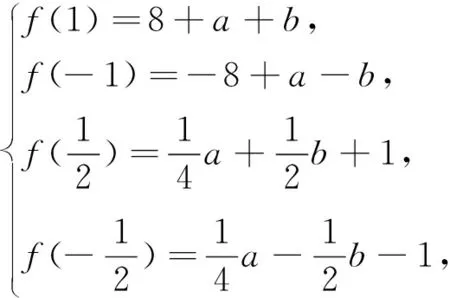
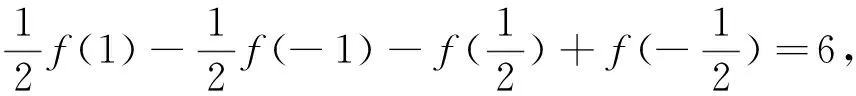
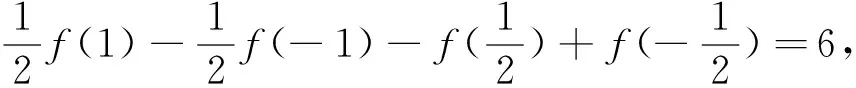
四、利用图像减损,恰好“顶天立地”时,找问题解决方案
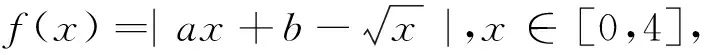
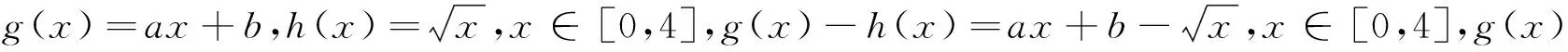
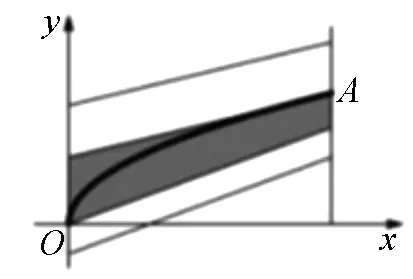
图5
首先,任意一条与抛物线E无公共点的线段,都可以通过平移,使其与抛物线E有公共点,并在此过程中,M(a,b)变小,如图5.
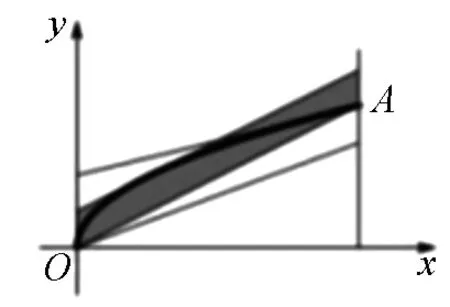
图6
反思:前面题中的天、地线是水平的,本题的天、地线是斜向的.这不影响问题的本质.
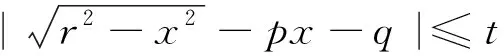
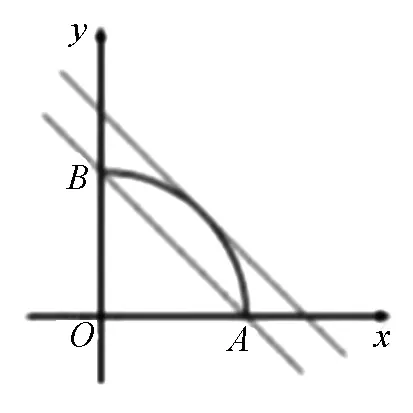
图7
解析:设f(x)=
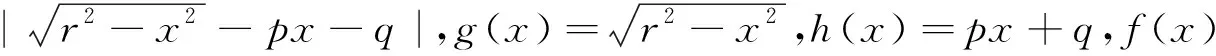
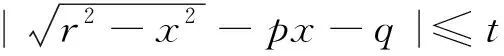
课堂教学中,要想让学生听懂,且印象深刻,就要从问题的本质入手,要做充分的铺垫.课堂教学中要讲透一道题,不仅要讲方法,还要讲内涵,讲背景,这样学生对这道题的认识是立体的.本文从图像变换及图像的叠加和减损的视角,来揭示一类多元参数题的内在本质,之中几何图像运动变化辅助较多,代数问题直观展示,形数互助,善莫大焉,这正如单墫教授在一书中写道:“数学大花园里,几何是最美的部分”[3],数学老师应该多用点时间把数学的直观美感展现给你的学生.
[1]波利亚.怎样解题[M],涂泓,冯承天译,上海科技出版社,2007.
[2]石秀福,王希年.一类二次函数考题的平移背景研究[J].中学教研(数学),2016(7)42-45.
[3]单墫平面几何的小花[M],上海教育出版社,2002.

