对一个征解问题的辨析与思考

安徽省阜阳市第三中学 (236000) 毛晓娜

在文[1]中，给出了一道解析几何题以及学生的一种解法，并询问学生的解法对吗？题目和解法如下：

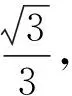
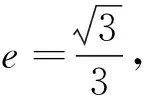
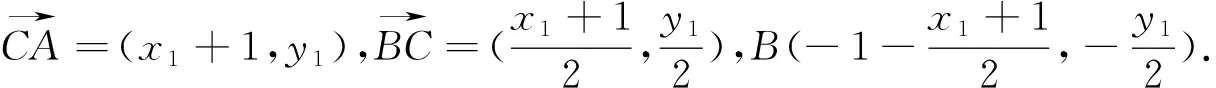
笔者认为学生的解法是错误的，并且解法中出现的几处错误还非常典型，下面笔者就学生解法的错误之处以及导致这种错误的原因谈一下自己的思考，与同行们交流.

1.设点A坐标时可以加限制条件y1>0吗?

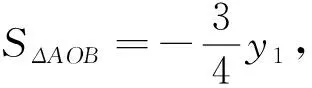
片断1：为了加强学生对双曲线定义的理解，给出了下面一道试题：

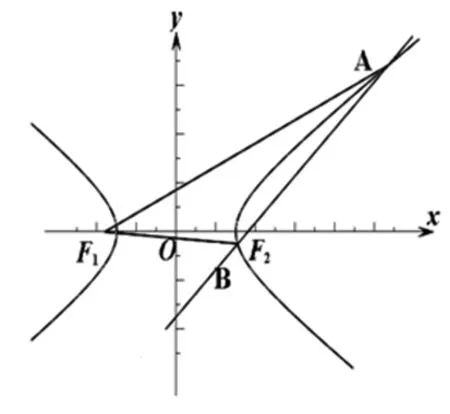
图1

|AF2|+|BF2|=|AF1|+|BF1|.

片刻以后，教师请一位同学回答

学生1：老师此题是错的，我认为|AF2|+|BF2|<|AF1|+|BF1|.

教师：你能给出解释吗？

学生1：在直角坐标系内作出图形(如图1)，通过图形可以发现A,B,F1构成三角形，利用三角形两边之和大于第三边得到|AF2|+|BF2|<|AF1|+|BF1|.

学生产生错误的根本原因在于作图的随意性，并没有将双曲线渐近线的倾斜角与直线l的倾斜角进行大小比较，来判断A,B两点是在y轴同侧还是两侧.

片断2：为了强调几何法在处理解析几何问题中的重要性，给出了下面一道试题：

已知抛物线的方程为x2=4y，焦点为E，直线l过点E与抛物线交于A,B两点，使得|AE|=

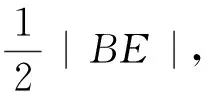
教师通过巡查发现，部分学生采取的是代数法，也有一部分同学利用的是几何法，所以特意选择一位利用几何法处理的学生回答.

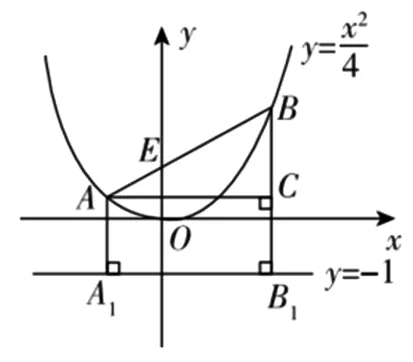
图2

学生2：如图2，设|AE|=m，则|AA1|=m，|BE|=|BB1|=2m,于是|BC|=m，在直角三角形ABC中，利用勾股定理可得|AC|=

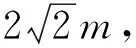
学生2的解法非常简洁，充分体现了几何法在解决解析几何问题中的作用，但是显然学生2漏掉斜率为负的情况，作为填空题，仍然不得分,在2012年高考数学新课标全国卷理科第20题中也是考查了这一点.

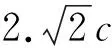
不妨先看看最值的定义，在人教A版教材中，“函数的最大值”的定义为(最小值的定义类似):

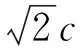
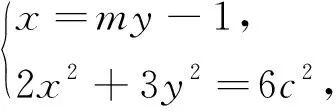
3.引发的思考

在处理数学问题时，经常会出现多个字母参数，有的字母是常数，有的字母是变量，有的字母看似变量，其实是常数，由于对字母参数理解错误导致出现争议或问题处理错误的情形经常出现，下面以两个案例加以说明.

案例1 我们都知道，所有偶数组成的集合可以表示为A={x|x=2n,n∈Z}，其中x为元素，n为参数，并且n每取一个整数得到集合中的一个元素，所以集合A表示无限集，在北师大版高中数学必修1第一章第一节习题B组给出下面一道题目：当a,b满足什么条件时，集合B={x|ax+b=0}分别为有限集、无限集、空集？

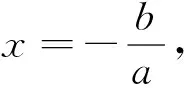
案例2 笔者所在学校高三年级的一次检测试卷中有下面一道试题：

已知函数f(x)=ln(x+1)-x.

(Ⅰ)求f(x)的单调区间;

阅卷后发现部分学生的解法如下：

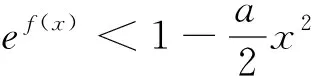
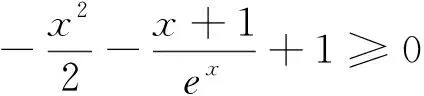
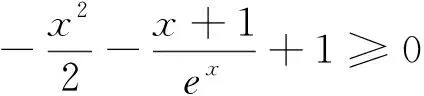
此解法认为字母参数a和x是两个没有依赖关系的变量，所以可以先选定a为主元，再令x为主元进行处理，那么学生的解法是否正确呢？

记φ(x)=x2+2x+2-2ex，x∈(0,+∞)，则φ′(x)=2(x+1-ex)，因为ex>x+1，所以φ′(x)<0，即φ(x)在x∈(0,+∞)单调递减，φ(x)<φ(0)=0，于是g′(x)<0，则g(x)是在(0,+∞)内单调递减的连续函数,且g(x)>0.

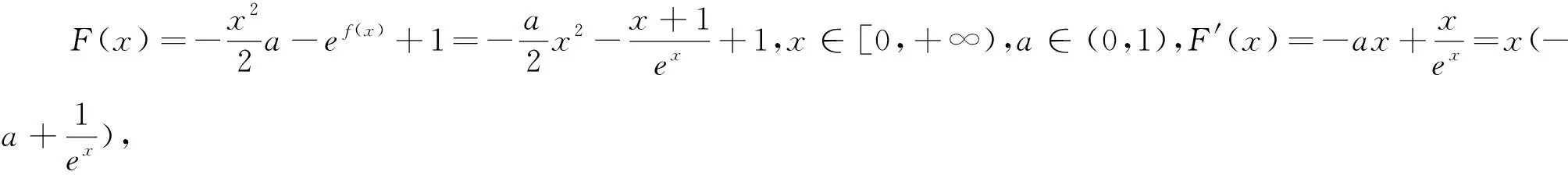
通过案例2的分析，给一类常见问题的解法提出了质疑，问题如下：

“y=f(x)与y=g(x)的定义域分别为I和D，对于任意x1∈I，总存在x2∈D，使f(x1)f(x)max，如果函数y=f(x)与y=g(x)都有最大值，这种解法固然没有问题，但是还应该有以下几种情况：

(1)如果y=f(x)的值域有上界，y=g(x)的值域无上界，一定满足要求;

(2)如果y=f(x)的值域无上界，y=g(x)的值域无上界，也满足要求;

由上面两个案例不难发现，无论是对题意的理解上，还是问题的解决上，弄清字母参数的真实含义是非常重要的，字母之间是相互独立还是存在依赖关系？哪些字母是变量？哪些字母是常数？这是解决问题之前必须认真思考的.

教学的主体是学生，明确学生所需与所惑是提高教学有效性的基本途径，学生的困惑是什么，导致困惑的原因是什么，如何解决困惑是进行教学之前必须解决的三个问题，在教学中对学生可能会产生的错误要做到有的放矢，敢于让学生犯错，在犯错中纠错，从而培养学生发现问题、提出问题、分析问题和解决问题的能力，真正意义上的实现新课程标准提出的高中数学课程总目标.

[1]王申旺.问题243[J].数学通讯(下半月)，2016(2)：37.

[2]耿合众.有限集还是无限集-兼谈字母参数的表达理解[J].中小学数学,2016(1-2):122-123.

[3]欧阳光中，朱学炎，金福临，陈传璋.数学分析(第三版)上册[M].北京：高等教育出版社，2007.