2017年高考数学江苏卷第12题的解法探究
2018-07-02 03:48:48湖北省大悟县楚才高级中学432800丁辉华
中学数学研究(江西) 2018年6期
湖北省大悟县楚才高级中学 (432800) 丁辉华
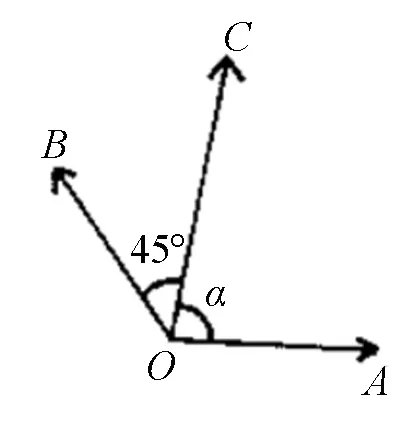
图1
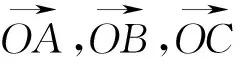
本题是2017年高考数学江苏卷第12题,试题温和平实,表述中规中矩,主要考查平面向量基本定理,平面向量数量积,两角和与差的三角函数公式.按江苏卷历年的风格,处于这个题号的题目,区分度较大,此题确实如此,它不仅考查学生综合运用向量知识,平面几何知识,解三角形知识及分析问题、解决问题的能力,还考查学生把握知识的能力,以及选择解决问题突破口的能力,能较好地检测学生的数学素养和进一步学习数学的潜能.下面从不同角度剖析本题,与读者交流切磋.
一、借助向量的数量积求解
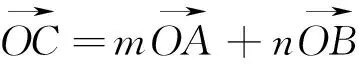
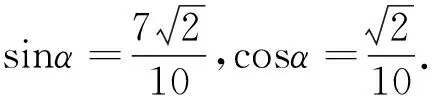
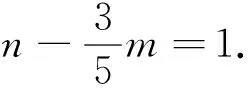
①+②得m+n=3.
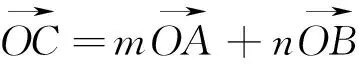
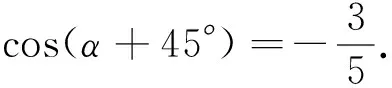
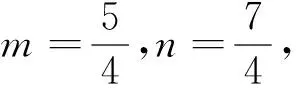
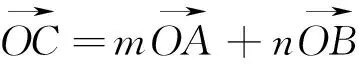
二、根据条件,构造图形求解.
平面向量基本定理本质上是向量加法的三角形法则、平行四边形法则的另一种表达形式,即通过基向量线性表达.本题根据条件,也可以利用平面图形的特征来解决.
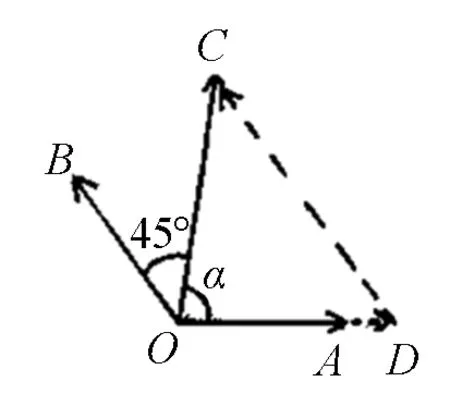
图2
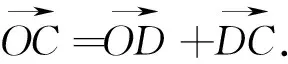
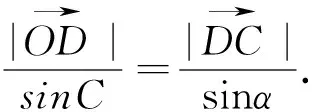
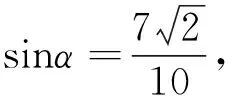
下面讨论m+n=4不符合题意.
D=180°-45°-α=135°-α.
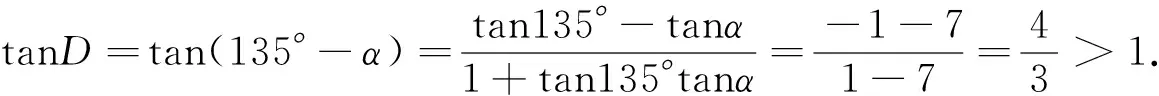
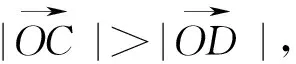
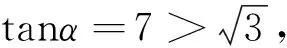
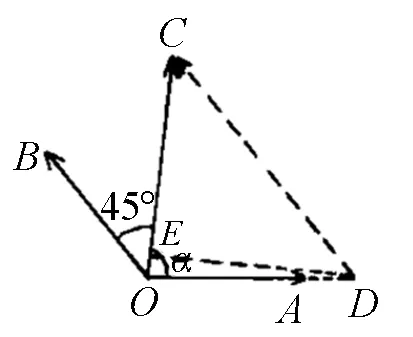
图3
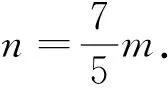
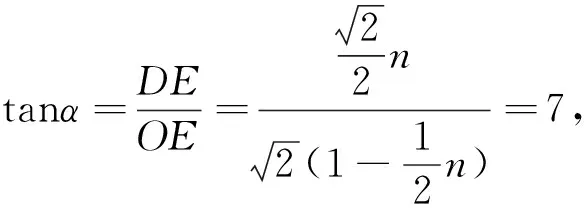
评注:解法3通过构造三角形,借助正弦定理、余弦定理确定出m,n的关系,由余弦定理确定出来的是m,n的二次关系式,这样有可能产生增解,从而导致错解.解法4在解法3的基础上加以改进,多了一条辅助线,通过解直角三角形,得到关于m,n的一次方程,可以准确地求出m,n的值.
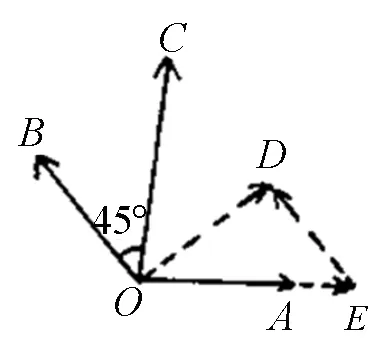
图4

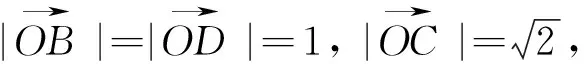
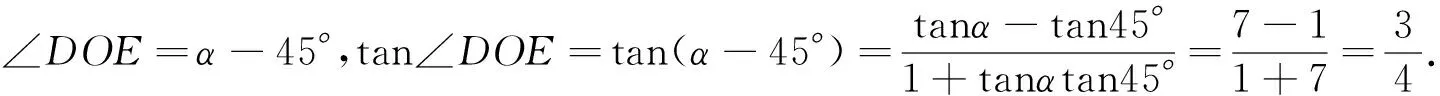
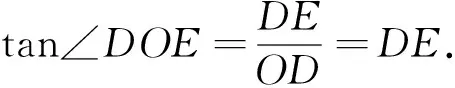
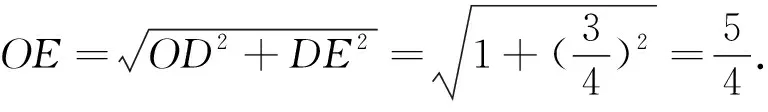
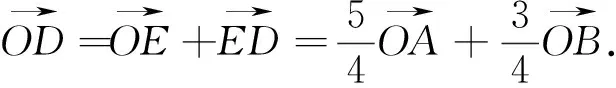
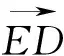
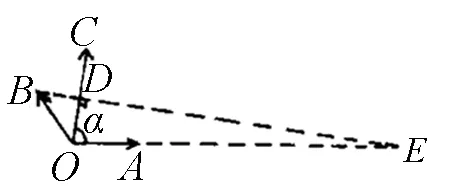
图5
解法6:过点B作OC的垂线,垂足为D,垂线交OA(或OA的延长线)于E,如图5.
∵∠BOC=45°,

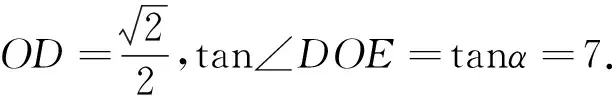
三、利用坐标法求解
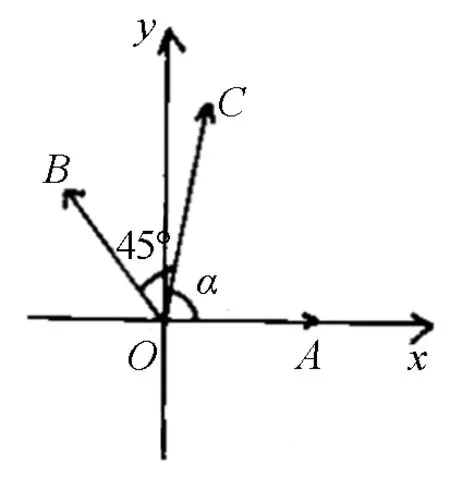
图6
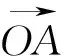
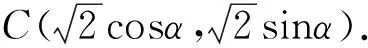

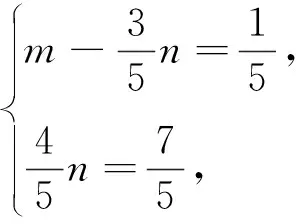
∴m+n=3.
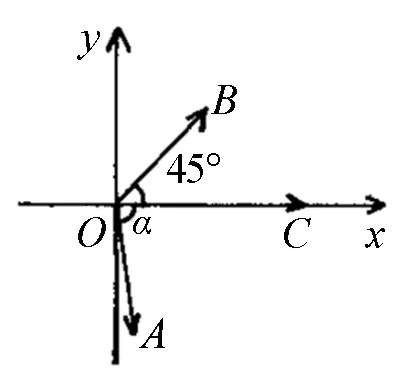
图7
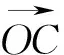
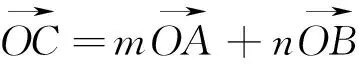
猜你喜欢
初中生学习指导·中考版(2023年9期)2023-09-30 15:22:41
新世纪智能(教师)(2021年2期)2021-11-05 08:43:18
小学生学习指导(中年级)(2021年10期)2021-11-01 08:17:08
海洋通报(2021年2期)2021-07-22 07:55:26
中学生数理化(高中版.高二数学)(2020年11期)2020-12-14 07:36:32
中学生数理化(高中版.高考数学)(2020年10期)2020-10-27 03:04:28
河北理科教学研究(2020年1期)2020-07-24 08:14:28
新高考·高二数学(2017年9期)2018-03-16 18:02:26
智富时代(2017年4期)2017-04-27 02:13:48
幼儿智力世界(2016年1期)2016-05-30 10:48:04

