巧用余弦定理证明一类三元无理不等式

江西省赣州市第一中学 (341000) 冯启轩 彭小明

引例已知x,y,z为正数，证明：

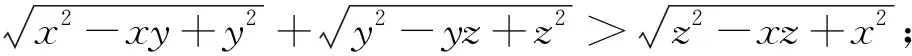
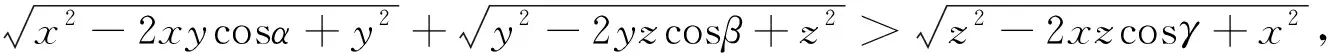
一、巧用余弦定理证明三元无理不等式

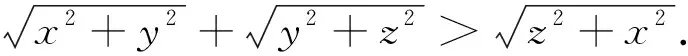
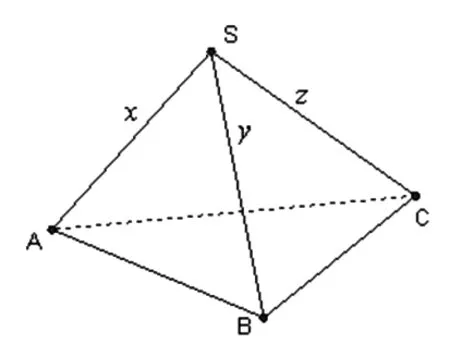
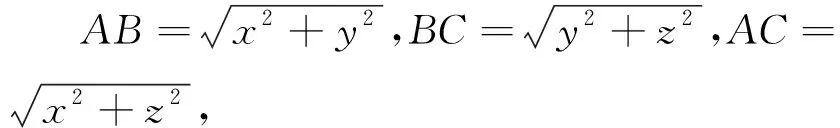
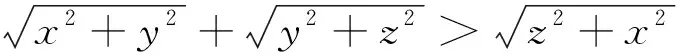
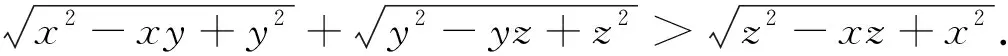
证明:构造一个三棱锥S-ABC，使∠ASB=∠BSC=∠CSA=60°，SA=x,SB=y,SC=z,AB=

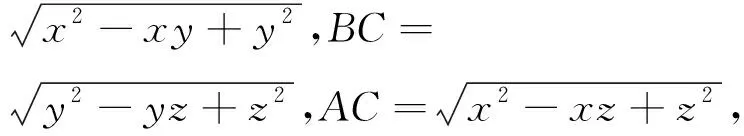
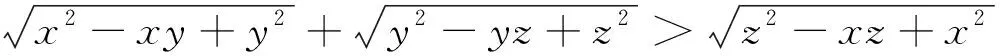
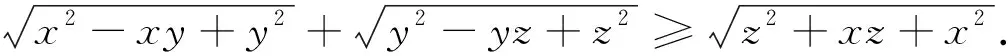
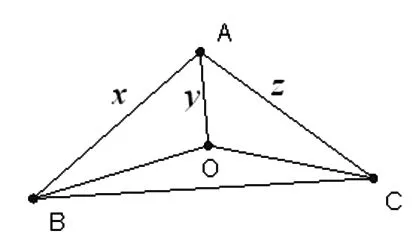
证明：在平面上任取一点A,作∠OAB=∠OAC=60°，取AB=x,OA=y,AC=z，连接BO,OC,BC,在ΔOAB,ΔOAC,ΔABC中由余弦定理可知BO=

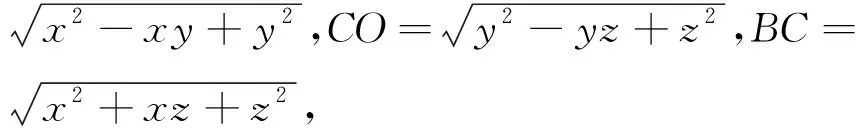
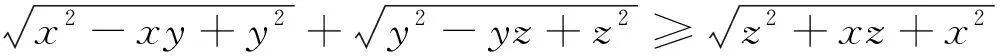
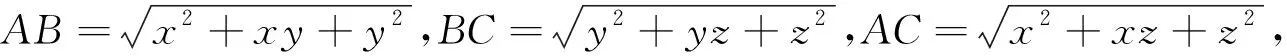
二、方法的推广

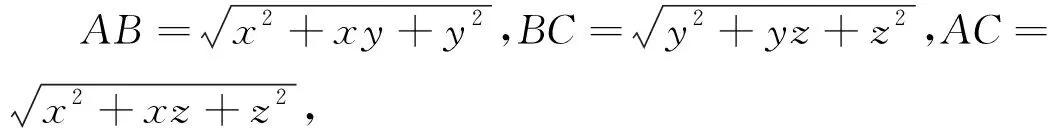
2.推广：设x,y,z为正数，α,β,γ∈(0,π)且α

证明：(1)当α+β+γ=2π时,在平面上任取一点O，作∠AOB=α,∠BOC=β,∠AOC=γ,且取OA=x,OB=y,OC=z，连接AB,BC,CA,如图，在ΔAOB,ΔBOC,ΔAOC中，由余弦定理可知AB=

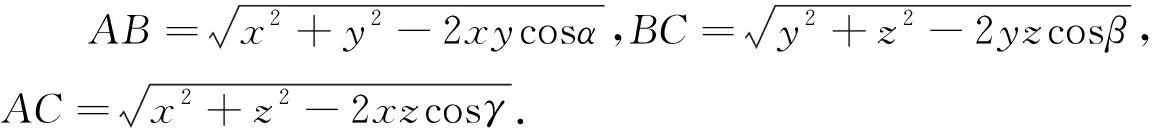
在ΔABC中易知AB+BC>AC,所以