构建知识网络，进行知识辐射，站在中心点解题——高三数学解题教学的一点思考

厦门大学附属实验中学 (363123) 田富德

数学课堂离不开解题教学，解题教学是数学课堂教学的一个重要组成部分，它不仅能有效地增强学生解决问题的能力，培养学生的思维能力，动手能力，创新能力，而且可以加深对基本概念的理解，促进学生良好的数学观念的形成.课程标准明确指出：要注重应用，加强对学生数学应用意识和解决实际问题能力的培养.

高三数学课堂更是以解题为主，进入高三总复习，学生已经结束高中新课的学习，对高中数学知识已经初步掌握，如何让解题教学的课堂更加有效？当学生面对新的数学问题时，应该怎样有效地去思考？传统的解题教学策略，如一题多解、多题一解、变式教学、题组教学等仍然可以有效继承.本文主要从如何通过回忆、联想，建立试题与知识、定理、公式等的联系，以试题的条件或问题为中心，站在知识网络的中心点进行知识辐射，进行解题.下面以一道习题为例展开分析.

引例若x2+y2=4，求x+y的最大值.

变式1 若x2+y2=4，求x+2y的最大值.

变式2 若x2+y2=4，求x+y2的最大值.

变式4 若x2+y2=4，求x2-6x+y2-2y+10的最大值.

变式5 若x2+2y2=4，求x+y的取值范围.

变式6 若x2+xy+2y2=4，求x+y的取值范围.

变式7 若x2+xy-2y2=4，求x+y的取值范围.

变式9 若x2+y2+z2=4，求x+y+2z的最大值.

变式10 设x,y,z∈R+，若x3+y3+z3=4，求x+y+z的最大值.

1.三角函数视角下的知识辐射

由条件“x2+y2=4”，联想到三角函数的公式sin2θ+cos2θ=1，故可以考虑三角换元利用三角函数的有界性进行解题.

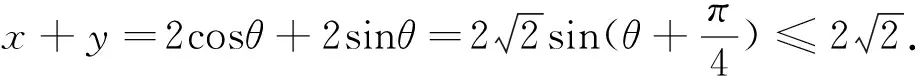
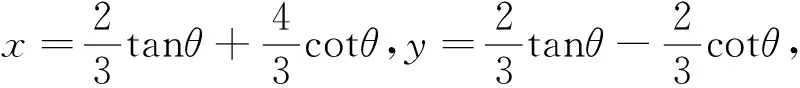
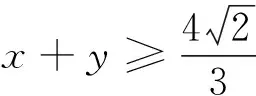
借助三角函数的有界性及变量的单一化，均可解答本文的变式1至变式6.

2.解析几何视角下的知识辐射

由条件“x2+y2=4”联想到圆的方程，此时必须将问题中的“x+y”与解析几何中的公式定理联系.解析几何中的常见公式有：两点间的距离公式(体现平方关系)、点到线的距离公式(体现线性关系)、斜率公式(体现比值关系)、线性目标函数(体现线性关系)等等，而x+y为线性表达式，故可考虑利用点到线的距离公式进行求解.

由问题“求x+y的最大值”，联想到线性规划中的线性目标函数z=x+y，约束条件“x2+y2=4”在平面直角坐标系中表示圆的方程，可将该圆看成可行域，利用线性规划的知识进行解题.

借助解析几何的知识，还可以解决本文的变式1、变式3至变式5.

3.二次方程视角下的知识辐射

观察到问题及条件均可视为关于x,y的二次方程(含其中一个为一次方程)，故可考虑利用二次方程解的存在性来进行解题.

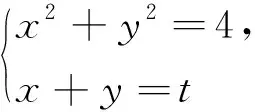
借助二次方程组存在性的知识，我们还可以解决本文变式1至变式3及变式5至变式7.

4.平面向量视角下的知识辐射

由问题“求x+y的最大值”，联想的平面向量的数量积，x+y=1·x+1·y，故可以考虑构造平面向量来进行解题.

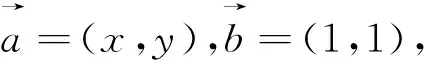
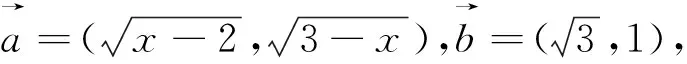
借助平面向量数量积的知识，我们还可以解决本文的变式1和变式5.

5.基本不等式视角下的知识辐射

求解二元(多元)最值问题的常用工具便是基本不等式，不等式求解问题注重齐次化，引例条件为二次，求解问题为一次的，只需将问题平方即可.

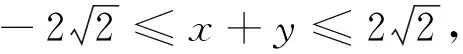
利用基本不等式解题，需要注意对系数的调整，可以用待定系数法求出适合的系数.

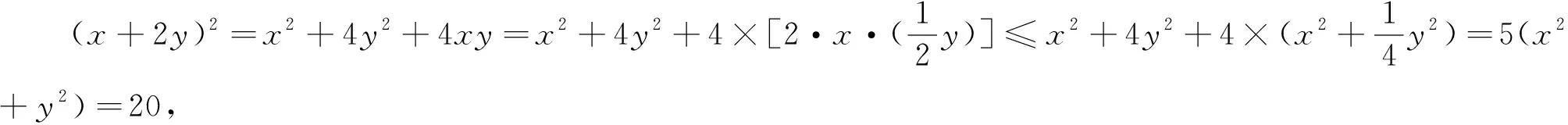
借助基本不等式，我们还可以解决本文变式5.

6.柯西不等式视角下的知识辐射

求解三元(多元)、三次(高次)的最值问题，用基本不等式则较为繁琐，而柯西不等式可成为最好的工具.

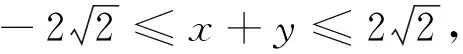
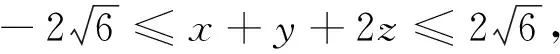
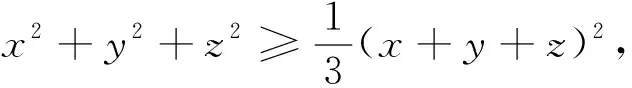
构建知识网络，以试题条件或问题为中心，站在知识网络的中心点进行知识辐射，在不同知识视角下，建立试题与所学的相关知识的联系进行解题，其实可以看成一题多解、多题一解、变式教学、题组教学的继承与延伸.在具体解题时，具体选择在那个知识视角下进行建立相互联系，需要对课本知识足够熟悉，知识体系足够清晰，需要教师在课堂教学不断的点拨，才能对每一道题选择适合的方法，才能对陌生的试题轻松找到解题突破口.

高三复习以解题教学为主，切忌满堂课都在就题论题，应选择适合的例题，进行知识辐射，站在知识网络的中心点进行解题分析，达到以点带面，对整个高中数学知识，时不时温故而知新，可以有效降低学生对知识的遗忘率，可以提高学生面对创新试题时解决问题的能力.