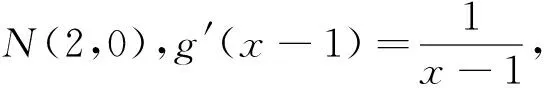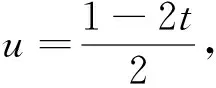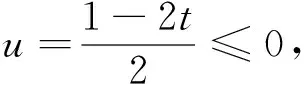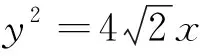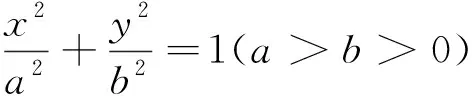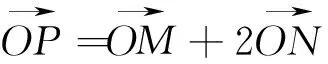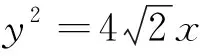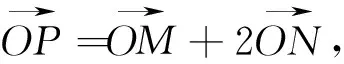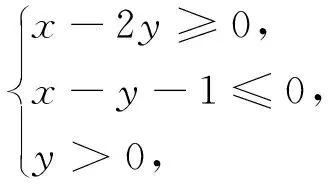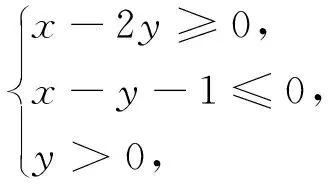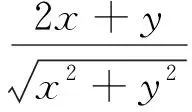关注相似结构 突破解题难点——谈数学联想的重要性

天津市耀华中学 (300040) 明廷军

认知学习理论认为：学生在学习时都以原有的认知结构为依据，将新知识进行加工，如果新知识与原有的认知结构中适当的知识相联系，那么通过新旧知识的相互作用，新知识就会纳入到原来的知识结构当中，从而扩大了它的内容，而新旧知识之间的这种相互作用就是通过新旧知识结构的相似性用旧知识来同化新知识.本文尝试着通过关注相似结构的方法来引导学生解决问题，进而培养学生的联想能力.

例1 已知函数f(x)=x2-ax(a≠0),g(x)=lnx,f(x)图像与x轴异于原点的交点M处的切线为l1，g(x-1)与x轴的交点N处的切线为l2，并且l1与l2平行.

(1)求f(2)的值；

(2)已知实数t∈R，求函数y=f[x·g(x)+t],x∈[1,e]的最小值；

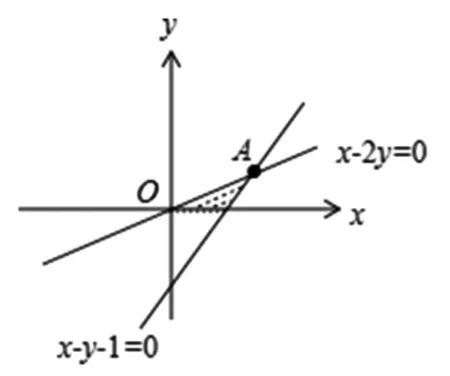
(3)令F(x)=g(x)+g′(x),给定x1,x2∈(1,+∞),x1

(2)y=f[x·g(x)+t]=[x·lnx+t]2-(x·lnx+t)=(x·lnx)2+(2t-1)·(xlnx)+t2-t,令u=xlnx,在x∈[1,e]时，u′=lnx+1>0，∴u=xlnx在[1,e]单调递增，0≤u≤e.

①当m∈(0,1)时，有α=mx1+(1-m)x2>mx1+(1-m)x1=x1,α=mx1+(1-m)x2

②当m≤0时，α=mx1+(1-m)x2≥mx2+(1-m)x2=x2,β=mx2+(1-m)x1≤mx1+(1-m)x1=x1,由F(x)的单调性知F(β)≤F(x1)

③当m≥1时，同理可得α≤x1,β≥x2,得|F(α)-F(β)|≥|F(x1)-F(x2)|,与题设不符.∴综合①、②、③得m∈(0,1).

(1)求椭圆标准方程；

(2)记△ABD与△ABC的面积分别为S1和S2，且|S1-S2|=2，求直线l方程；

(3)存在两定点F1,F2使得|PF1|+|PF2|为定值.

小结：本题第(3)问中提及是否存在两个定点F1、F2使得|PF1|+|PF2|为定值，这让我们很容易联想到椭圆的第一定义，于是研究点P的轨迹方程就成了解题的一个很重要方向，如果能确定点P的轨迹就是椭圆，那么|PF1|+|PF2|这个定值就能很快定下来，它规避了直接求|PF1|+|PF2|的困难，关注相似结构为我们提供了数学发现的重要方法.

图1

在数学学习的过程当中，关注相似结构，进行知识之间的联想尤为重要，因为联想为我们提供了类比的方向，而类比不仅仅是学习概念、定理和法则的认知工具，更是我们解决数学问题的一种很重要的方法.