深研教材，让概念教学在学生心中落地生根——“比例的意义和基本性质”教学设计与意图

山东省青岛市崂山区东泰小学 韩同成 执教

山东省青岛市崂山区教科研与培训中心 张云萍 指导

【教学内容】《义务教育教科书·数学》（青岛版）六年制六年级下册第三单元信息窗1。

【教材分析】

本信息窗内容是学生掌握了比的知识的基础上进行学习的，教材尊重学生的认知基础，并以学生熟悉的啤酒生产原料运输为素材，通过本信息窗的学习，使学生理解比例的意义和比例的基本性质，并为今后的数学学习和其他学科的学习打下基础。

【教学目标】

1.理解比例的意义和基本性质，能用不同的方法判断两个比是否能组成比例；

2.经历比例基本性质的探索过程，培养学生初步的猜想与验证、观察与概括能力。

3.在探究的过程中，培养积极参与数学学习活动的兴趣，形成合作学习的意识，感受学习数学的乐趣。

【教学重点】比例的意义和性质的理解与应用。

【教学难点】比例意义和性质的探究。

【教学过程】

一、创设情境，复习引新

谈话：同学们，你们知道青岛都有哪些产品非常有名？（学生根据自己的了解回答）青岛啤酒享誉世界各地，这节课，我们将一起去探索啤酒生产中的数学问题。

出示课件：这是一辆货车正在运输啤酒的主要生产原料——大麦芽。

这是它两天的运输情况：

第一天 第二天运输次数 2 4运输量（吨） 16 32

从图中，你得到了哪些数学信息？

引导：根据表格信息，写出这辆货车每天运输量与运输次数的比。

预设：第一天，运输量与运输次数的比是16：2；第二天运输量与运输次数的比是32：4.（板书：16：2 ；32：4）

追问：根据表格中的信息，你还能找到那些比？

提问：比是我们以前学过的内容，你还记得怎么求比值吗？

预设：用比的前项除以后项得到的商就是比值。

谈话：请你求出16：2 和32：4这两个比的比值。

预设：16：2=8；32：4=8

二、引导探索，学习新知

（一）理解比例的意义。

引导：像16：2=8；32：4=8这样比值相等，说明这两个比相等，那么这两个比之间可用什么符号连接？

预设：等号（师擦去比值，在两个比之间用彩笔添上“=”）

谈话：请你接着求一下其它比的比值，看看能不能再找到相等的比用等号连接起来？

预设：2：16=4：32 4：32 = 2：16

2：4=16：32 16：32 = 2：4

4：2=32：16 32：16 = 4：2

引导：数学就是这么简单，一不小心就创造出了新知识。像这样的式子叫比例。（板书：比例）你能说说什么是比例吗？同桌的同学交流一下。

预设：两个比相等的式子叫比例（根据学生回答完整板书：表示两个比相等的式子叫做比例。）

巩固练习：下面是不是比例，为什么？

2． 0.3：0.4和3：4

预设：这只是两个比，不是比例，比例是个等式。

追问：这两个比能不能组成比例？你怎么判断？

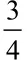
小结：通过这个练习，你想提醒大家什么？

（二）自主学习，认识比例的各部分名称。

谈话：组成比例需要两个比，也就是四个数，组成比例的这四个数，有自己的名称，请大家看书自学比例的各部分名称。

学生自学。

交流：谁来交流一下你的收获？

预设：a：组成比例的这四个数叫做比例的项。两端的两项叫做比例的外项，中间的两项叫做比例的内项。如16∶32= 2∶4中16、4是外项，32、2是内项。（板书：内项和外项）

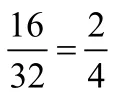
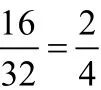
（三）探究比例的基本性质

1.研究素材，猜测规律

引导：仔细观察这些比例，你有什么发现？把你的发现和小组内的同学交流一下。

学生小组内交流。

无论在哪个时期，茅台与人民军队结下的红色情缘是其他企业都难以比拟的。1988年，茅台酒厂组织慰问团队，赴云南老山边防前线慰问部队指导员，留下了“品国酒、壮国威、千里南疆老山行”的佳话，开启了茅台集团军企共建的时代征程。从那时起，每年建军节期间，茅台集团都会组织慰问团队，赴边关踏雪域，到边疆访海岛，慰问部队官兵。

班内集体交流。

预设：在比例中，两个外项的积等于两个内项的积。

追问：刚才，我们发现了在一个比例中，两个内项的积等于两个外项的积，那它们的和、差、商之间是不是也有这样的关系呢？

学生举例说明。

2.讨论交流，验证规律

班内展示验证过程。

小结：在比例里，两个外项的积才等于两个内项的积，这个规律就是比例的基本性质。（板书课题。）猜想、验证、总结是我们数学学习经常用到的解决问题的方法。

三、自主练习，巩固提高。

1.基本练习

(1)利用比例的意义或基本性质，判断下面哪组中的两个比可以组成比例

(2)在a：7=9：b中，（ ）是内项，( ）是外项，a×b=( )

2.变式练习

(1)在比例里，两个内项的积是18，其中一个外项是2，另一个外项是（ ）。

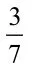
3.拓展练习

(1)12：3=4：( )。追问：你是怎么想的？根据是什么？

四、全课小结，畅谈收获

谈话：同学们，40分钟马上就要到了，让我们来谈谈收获吧！咱们从学会了什么知识，掌握了什么方法，有什么感受这三个方面来谈，好吗？