融入差异性的帕累托集成剪枝方法

魏苗苗 杭 杰

(南京邮电大学计算机学院，南京， 210003)

引 言

分类与回归是监督学习研究中的基本任务。分类与回归最终的目标是在一个由各种可能的函数组成的假设空间中搜索与实际目标分类函数最接近的分类器，使该分类器尽可能精确地分类未知实例。然而，单个学习器在某些情况下的泛化性能是有限的。为了提高学习器的泛化性能，学者们提出了集成学习的思想。1997年Dietterich[1]指出集成学习将会成为机器学习领域的4大研究方向之首。

集成学习是使用多个学习器共同决策的过程。集成学习一般可以分为两个步骤：(1) 产生多个不同的基分类器，(2) 采用某种集成策略(如投票法)来决定最终的分类结果[2]。按照基分类器之间的种类关系，可以把集成学习分为同质集成学习和异质集成学习[3]。同质集成学习是集成多个同种类的基分类器，该同种类的代表分类器可以是人工神经网络、决策树、朴素贝叶斯和K-近邻等。而异质集成学习是集成多个各种类别的基分类器，其中代表的基分类器有叠加法[4]和元学习法[5]等。随着机器学习领域不断深入的研究，集成学习已经应用到多个领域。在传统的集成学习中，大多数的方法是先产生多个不同的弱分类器，再由所有的基分类器构建一个强分类器。尽管这种方法可以有效地提高分类器的泛化性能，但是该方法存在一些不足：集成所有的基分类器将消耗大量的时间和空间资源；预测速度也随着基分类器的增多而急剧下降。于是，Zhou等[6]于2002年首次提出了“选择性集成”的概念，选择性集成的思路是选用部分基学习器集成的效果可能比集成所有的基分类器效果更优。

集成剪枝又称选择性集成、集成简化，它是在训练出所有基学习器之后，基于某种准则，选择一部分基学习器(所有基学习器的一个最优子集)进行集成，最终得到一个强分类器。集成剪枝的过程主要包括3步：产生不同的分类器；根据验证集选择最优的分类器子集；集成分类器子集。集成剪枝方法的异同主要取决于剪枝策略。剪枝策略可以根据分类器的不同划分为基于分类问题的剪枝策略和基于回归问题的剪枝策略。由于在回归问题中，集成剪枝问题研究的较少且效果不明显，所以本节主要讨论基于分类问题的剪枝策略。Tsoumakas[7]等总结了集成剪枝的多种策略，文献[8-15]中将集成剪枝策略分为基于排序的剪枝，基于聚类的剪枝，基于优化的剪枝以及其他方法的剪枝。

剪枝过程中使用的剪枝策略决定了集成剪枝的方法。目前还没有确定的最佳剪枝策略方法，已有的代表性剪枝策略使用遗传算法进行剪枝[6]，采用人工免疫算法进行剪枝[16]，用聚类算法进行剪枝[9]，2015年，Qian等又采用帕累托(Pareto)占优的双目标优化思想进行剪枝[17]。然而采用遗传算法和人工免疫算法剪枝的复杂度相当高；利用聚类的中心参与集成剪枝的聚类算法也忽略了单个学习器有限的泛化性能；Pareto占优的双目标优化集成剪枝忽略了分类器之间的差异性。因此，为了改进上述方法的不足，在Pareto集成剪枝的基础上，本文提出了融入差异性的Pareto集成剪枝方法。

1 融入差异性的Pareto集成剪枝

1.1 Pareto集成剪枝方法

在工程与科学计算领域中，存在着许多多目标优化的问题(Multi-objective optimization problem, MOP)。多目标优化问题的有效解也称为Pareto最优解。集成剪枝方法有两个目标：最小化集成的基分类器的个数以及最大化集成后分类器的泛化性能。对于这两个目标，研究者首先想到的是将这两个目标通过某种数学模型整合为一个优化目标。虽然这种方法存在一定的道理，但是这种合二为一的方法也与最初的集成优化目标有所偏差。文献[17]方法将最小化基分类器的个数和最大化分类器的泛化性能作为两个单独的优化目标共同优化。

(1)

在该双目标优化中，f(Hc)表示选中的|c|个分类器的泛化误差，|c|表示集成规模。定义1介绍两个目标之间的Pareto占优关系。

定义1[17]Pareto占优或Pareto支配：令存在一个双目标函数φ=(φ1,φ2)，C表示所有解决方案向量的集合。若存在两个不相等的解决方案c，c'∈C，则有

(a)c弱占优于c'，当满足φ1(c)φ1(c')并且φ2(c)φ2(c')时，表示为c弱占优于c'。

(b)c占优于c'，当满足c弱占优于c'且同时满足φ1(c)<φ1(c')或者φ2(c)<φ2(c')，表示为c占优于c'。

若在所有解决方案的集合C中，若没有任一个方案占优于c，那么c就是Pareto最优的解决方案。而初始化解决方案c的方法是随机产生的一个由0，1组成的向量，并将此向量放入候选方案集合C中；然后通过迭代更新C中的解决方案。每次迭代都将在C中随机挑选一个解决方案c，给c一定的扰动使之生成c′；若C中没有任何一个方案能够占优于c′，则将c′加入集合C中，同时将集合C中被c′弱占优的方案去除。而对于每次迭代过程中生成的c′，文献中采用可变深度搜索[17](Variable depth search，VDS)的方法(见算法2)，搜索出与c′相距一个汉明距离的所有解决方案。在这些解决方案中若能搜索出可占优于c′的解决方案，则用该占优的解决方案代替c′。将c′从C中去除。深度优先搜索的方法是有序的局部贪心搜索，每次搜索都选择局部最优解。为了避免重复搜索，算法中引入一个L变量，用于记录已被搜索过了的路径。最终从候选集合C中选出泛化误差最低的解决方案作为双目标的问题的解。

算法1Pareto集成剪枝

输入：

一系列已训练的分类器H={hα}nα=1，第一个目标函数f(Hc)，第二个目标|c|,评价准则evaluation

输出：argminc∈Cevaluation(c)

1．令F(c)=(f(Hc),|c|)为待优化的双目标函数。

2．初始化c为一个n维向量，元素由0,1随机组成。

3．Repeat

4．在集合C中随机抽取一个方案c

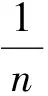
7.C=(C-{z∈C|c'弱占优于z})∪{c′}

8.Q=VDS(e，c')

9.forq∈Q

11.C=(C-{z∈C|q弱占优于z})∪{q}

算法2可变深度搜索(Variable depth search，VDS)

输入:一个伪布尔函数e,一个解决方案c

输出：Q

(1)Q=ø，L=ø

(2) 令N(·)为与解决方案c相距一个汉明距离的所有解决方案的集合

(3) While

Vc={y∈N(c)|(yk≠ck⟹k∈L)}=ø

(4) 选择使得e达到最小值的y∈Vc

(5)Q=Q∪{y}

(6)L=L∪{k|yk≠ck}

(7)c=y

在该双目标优化中，第1个目标是最大化分类准确率，第2个目标是最小化剪枝后分类器的个数，即集成规模。算法1的(6～7)和(9～11)步已经决定了搜索的路径方向，因此不会存在只优化其中一个目标的问题。VDS只是搜索局部最优值，不影响最优解决方案的搜索方向。评价准则evaluation可以根据侧重点来选取，更加侧重分类准确则在剪枝后的集合C中根据f(Hc)函数选取最优的解决方案，若更加侧重集成分类器的规模，则根据分类器的个数|c|选取。采用已选取的分类结果在验证集上的泛化误差来衡量泛化性能f(Hc)，f(Hc)越小代表泛化性能越高；将差异性和泛化误差都归一化到(0,1)之间，使得目标结果g(c)满足越接近0泛化性能越好、差异性越大。剪枝过程完成后，采用熵度量[18]衡量分类器之间的差异性，该差异性也被归一化到(0,1)之间，且越接近0差异性越小。算法1中的(3)循环的次数设为|-n2logn-|[17],实验选出最优的分类器子集之后，采用多数投票的方法进行集成。

1.2 融入差异性的集成剪枝

分类器集成中的差异性学习途径通常可以分为两种，隐性差异性和显性差异性。隐性差异性是指通过不同的数据训练不同的基分类器，隐性地使得各分类器具有差异性，如Bagging[19],Boosting[20]；显性差异性是指最大化某个与差异性相关的目标函数来集成不同的分类器，如半定规划[21]。本文研究的差异性是隐性差异性与显性差异性的组合，实验前期使用Bagging[19]训练不同的基分类器，后期使用融入差异性的目标函数对分类器进行剪枝，使之为集成提供差异较大的基分类器的集合。差异性是提高集成泛化能力的必要条件，对于提高集成学习的泛化能力具有重要意义，有关差异性的研究是研究集成学习的基础。Ali等[22]指出只有当分类器集合中各个分类器具有显著的互补性，它们的集成效果才能充分体现。

Pareto集成剪枝方法可以提高分类精确度、缩减集成规模，然而在分类器差异性这方面的工作仍是空白。集成学习需要有差异性，分类器之间的差异性可以确保分类器之间的相互独立性，若一系列分类器的集成效果突出，那么分类器之间的差异应足够包含分类的错分类型。在差异性研究的基础上，本文提出了融入差异性的帕累托集成剪枝方法(Pareto ensemble pruning with diversity, PEPD)。该方法将差异性的度量融入Pareto集成剪枝算法的第1个目标中，第2个目标仍是集成规模。因此，PEPD算法可以同时优化精准度，差异性以及集成规模这3个目标。

差异性学习和分类器准确率度量在集成学习中有着不同目的和算法处理过程。因此，实施这些不同的学习策略算法最初是分开的、独立的。Yin等[23]提出将差异性与稀疏性线性相加为一个优化目标的方法。而本文是在该Pareto占优的双目标优化的基础上，在泛化目标中线性增加了差异性度量，以增加差异性对于剪枝策略的影响。第1个优化目标更改为泛化误差和差异性的线性结合体：minc(μf(Hc)+λd(Hc))，第2个优化目标仍是集成规模min|c|。那么融入差异性的帕累托集成剪枝方法的目标函数可以表示成

(2)

其中，融入差异性的集成d(Hc)表示该|c|个分类器之间的差异性。μ(0<μ<1)和λ(0<λ<1)是调节泛化误差和差异性之间所占比重的参数，μ+λ=1。根据数据集的不同对参数μ、λ进行调节。为了减少f(Hc)和d(Hc)函数值本身对优化目标即线性函数的影响，实验中将f(Hc)和d(Hc)都进行了归一化处理。

算法3融入差异性的Pareto集成剪枝算法

输入：

一系列已训练的分类器H={hα}nα=1，第1个目标函数g(c)=μf(Hc)+λd(Hc)，第2个目标|c|,评价准则evaluation

输出：argminc∈Cevaluation(c)

1．令F(c)=(g(c),|c|)为待优化的双目标函数。

2．初始化c为一个n维向量，元素由0,1随机组成。

3．Repeat

4． 在集合C中随机抽取一个方案c

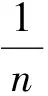
7.C=(C-{z∈C|c'弱占优于z})∪{c'}

8.Q=VDS(e，c')

9.forq∈Q

11.C=(C-{z∈C|q弱占优于z})∪{q}

将该融入差异性的改进算法与算法1相比较，首先将输入的第一个优化目标改为g(c)=μf(Hc)+λd(Hc)；其次，在每一次的占优、弱占优的比较中，目标函数φ1=μf(Hc)+λd(Hc)，φ2=|c|，即在每1次的迭代比较中，都会将分类器子集的分类准确率，各分类器间的差异性以及集成规模做对比。若某解决方案c的第1个目标优于另一解决方案c′的第1个优化目标，而c的第2个优化目标劣于c′的第2个优化目标，即|c|>|c′|。它们都不满足任一方占优或弱占优另一方的情况，那么将这两个解决方案均加入解决方案集合C中。直到某次迭代中存在其他方案能够占优于c或c′，将c或c′顶替出集合。若不存在其他解决方案可以占优c、c′，则在挑选最终解决方案时，按照evaluation进行筛选。evaluation是按照相同集成规模选择具有最优第1目标的剪枝方案，为确保集成剪枝方法不降低集成分类精准度，因此在不同集成规模时也选择最优第1目标的剪枝方案。

1.3 差异性度量

单分类器之间的差异性在集成学习中起着至关重要的作用。然而到目前为止，在学术界还没有一个可被公认的差异性的定义，因此，明确定义分类器之间的差异性比较困难。Kuncheva等对比了不同差异性度量的方法并且分析了它们与集成准确率之间的关系[24]。这些度量差异性的方法可以分为成对的差异性度量(Q统计量，相关系数，不一致度量以及双错度量)和非成对的差异性度量(熵度量，KW方差以及难点度量)两个类别。为了验证融入差异性的集成剪枝方法确实对集成泛化性能有提升作用，可以在差异性度量的两类方法中分别选取一个度量方法。

已知剪枝后的分类器个数θ=|c|，则剪枝后的分类器可表示为Hc={h1,h2,…,hθ}，N表示测试集中的样本数。根据剪枝后的分类器对测试样本的预测，可构造一个矩阵W=[wα,j]θ×N用于度量分类器之间的差异性。当wα,j=1时，表示第α个分类器对测试集中第j个样本的正确预测，反之，wα,j=0表示错误预测。两种差异性度量的方法详述如下。

(1) 不一致度量

(3)

其中

(4)

d(Hc)=1-DIS

(5)

(2) 熵度量

(6)

(7)

d(Hc)=1-ENT

(8)

其中，不一致度量为成对的差异性度量方法，熵度量为非成对的差异性度量方法。两种度量方法都将差异性d(Hc)限定在(0,1)范围之间，d(Hc)越接近于0代表差异性越大，反之d(Hc)越接近于1代表差异性越小，与泛化误差函数f(Hc)恰好保持一致收敛。

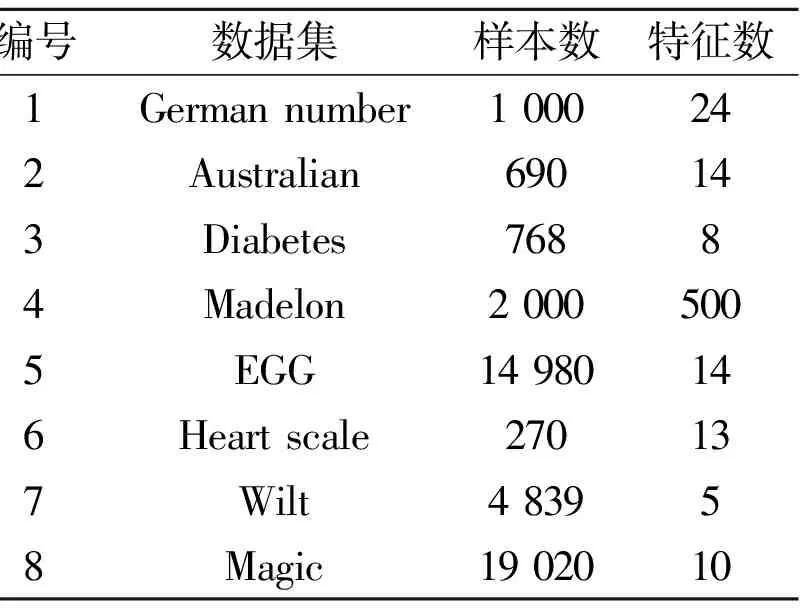
表1 实验中的8个真实数据集

2 实验评价与分析

2.1 数据集

为验证提出的融入差异性的Pareto剪枝方法的有效性，选择8个公开的UCI数据集进行实验。数据集的详细信息如表1所示。若实例个数为r，根据数据集的大小将数据集划分为3种规模：小规模数据(010 000)。每个规模的数据都选取2-3个数据集，则数据集的大小可以从270涵盖到19 020。实验将对比多个数据集在不同剪枝方法下的泛化能力以及分类器之间的差异性，如表1所示每个数据集对应一个编号，图1～6中的横坐标对应的编号也如此。

2.2 评价度量

在评价模型的性能时，评价指标起着至关重要的作用。对于分类器的集成，通常的评价指标有分类精准度、错误率或差异性来衡量。本实验将泛化误差和差异性综合为一个评价度量，即

g(c)=μf(Hc)+λd(Hc)

(9)

其中f(Hc)为分类器子集的泛化误差函数，d(Hc)为熵度量(非成对的差异性度量方法之一)或者不一致度量(成对的差异性度量方法之一)。由于泛化误差函数和差异性函数都归一化到(0,1)之间，而且值越小泛化性能及差异性能越好，参数μ，λ满足μ+λ=1，可以分别定义为0.5和0.5，也可以根据数据集的不同做适当的调整。第1个优化目标分别融入两种不同差异性度量方法(熵度量和不一致度量)作为评价准则，将该改进算法剪枝后的分类器之间的差异性与Pareto集成剪枝后的分类器之间的差异性做对比实验，使用熵度量方法衡量剪枝后分类器间的差异性。

2.3 实验结果及分析

2.3.1 实验结果

本实验主要对比Bagging集成、Pareto集成剪枝方法以及融入差异性的Pareto集成剪枝方法，分别记为Bagg, Bagg_Prun和Bagg_Div_Prun。选择对数据扰动比较敏感的k近邻分类器[25]和C4.5决策树分类器[26]分类器用于实验。随机抽取数据集的60%用于训练分类模型(Train)，余下40%的数据中一半作为验证集(Validation)，另一半作为测试集(Test)。根据数据集的大小训练出多个基分类器，数据集较大则训练的基分类器个数较多，反之训练个数较少。将基分类器在测试集上的预测结果转化为一个预测矩阵P=[p1,p2,…,pn]，代表n个分类器对同一个测试集的不同预测结果向量，其中pα={p1α,p2α,…,pTα}表示第α(α∈[1,n])个分类器在T个测试样本中的预测结果，ptα表示第α个分类器对第t个测试样本的预测值，预测正确则ptα=1，反之ptα=-1。

2.3.2 结果分析

实验对比了集成学习和集成剪枝的预测效果，以及融入差异性的集成剪枝和未融入差异性的集成剪枝的预测效果。如表2，3所示，表中粗体数字代表融入差异性的集成剪枝方法得到更优的分类效果。如图1，2所示，集成剪枝后的预测能力比集成学习的预测能力稍强，加入差异性的集成剪枝比没有加入差异性的剪枝策略泛化性能高。如图3，4所示，集成学习中基分类器的规模较大，而两种集成剪枝的基分类器规模相当且都比集成学习的规模要小许多，剪枝后的泛化性能与集成学习的泛化性能相当或者稍高，表明剪枝策略在不降低泛化性能的基础上有效减少集成学习的时间和空间资源的消耗，融入差异性的集成剪枝与Pareto集成剪枝方法集成规模相当，但能获得更高的泛化性能(图1,2所示)。分别采用不一致度量(成对)和熵度量(非成对)的差异性度量方法融入目标1中，再综合泛化误差对剪枝模型进行筛选。最后统一使用熵度量的方法分别衡量两种剪枝方法(PEP与PEPD)的分类器之间的差异性，实验结果如图5，6所示。图5,6表明，融入差异性的集成剪枝策略确实能够提升分类器之间的差异性。

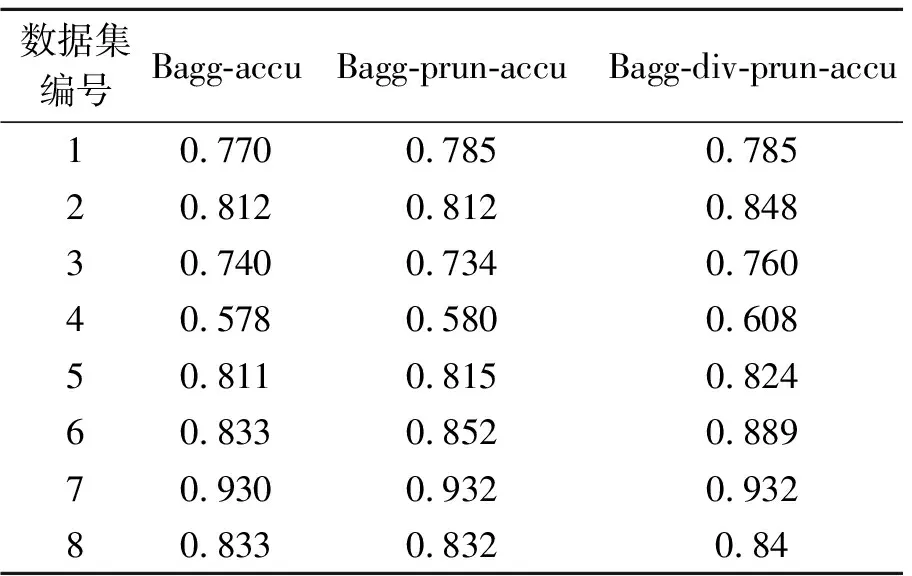
表2 基于KNN的不同集成剪枝方法准确率对比

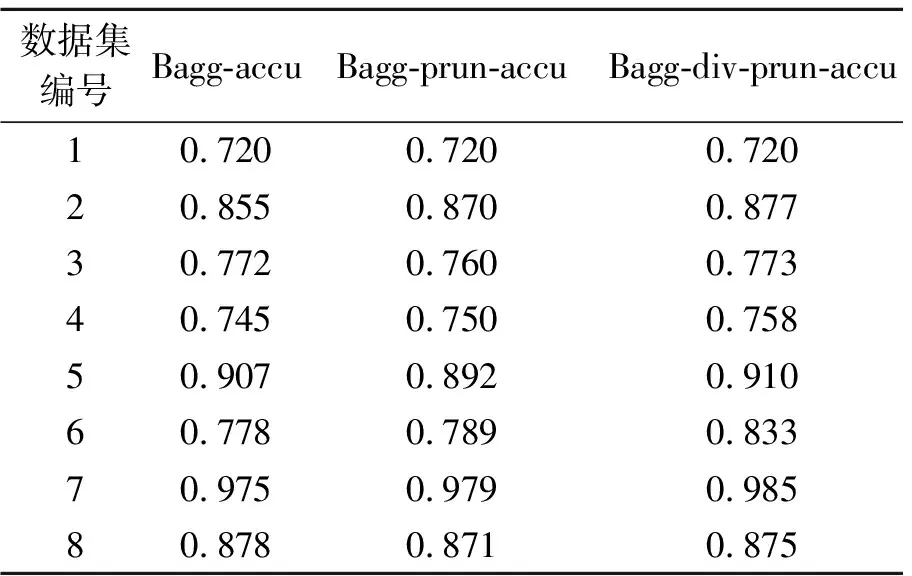
表3 基于C4.5的不同集成剪枝方法准确率对比

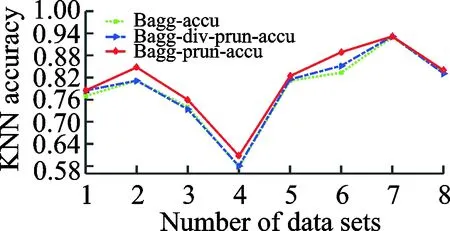
图1 基于KNN的不同集成方法准确率

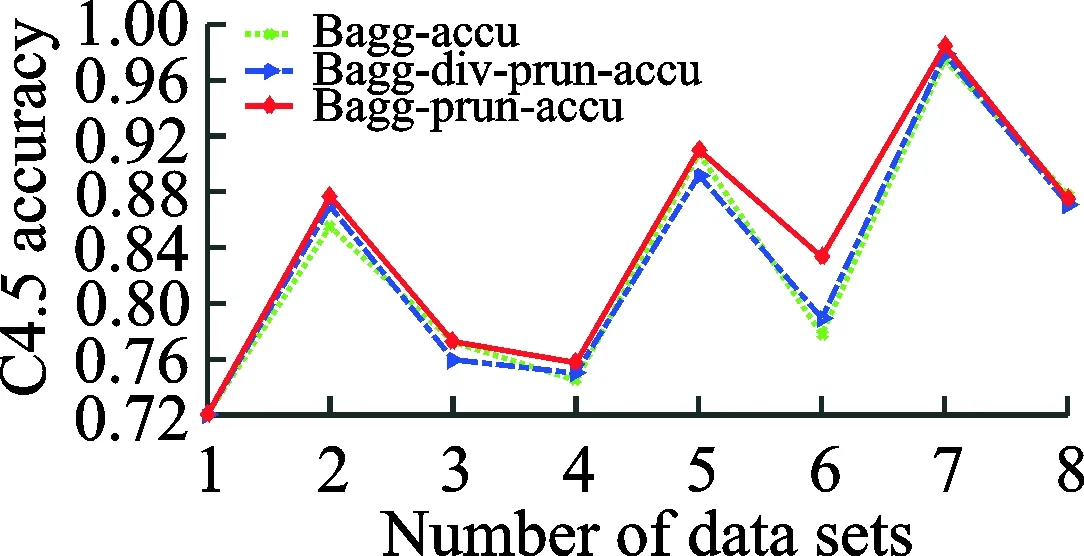
图2 基于C4.5的不同集成方法准确率

图3 基于KNN的不同集成剪枝方法集成规模

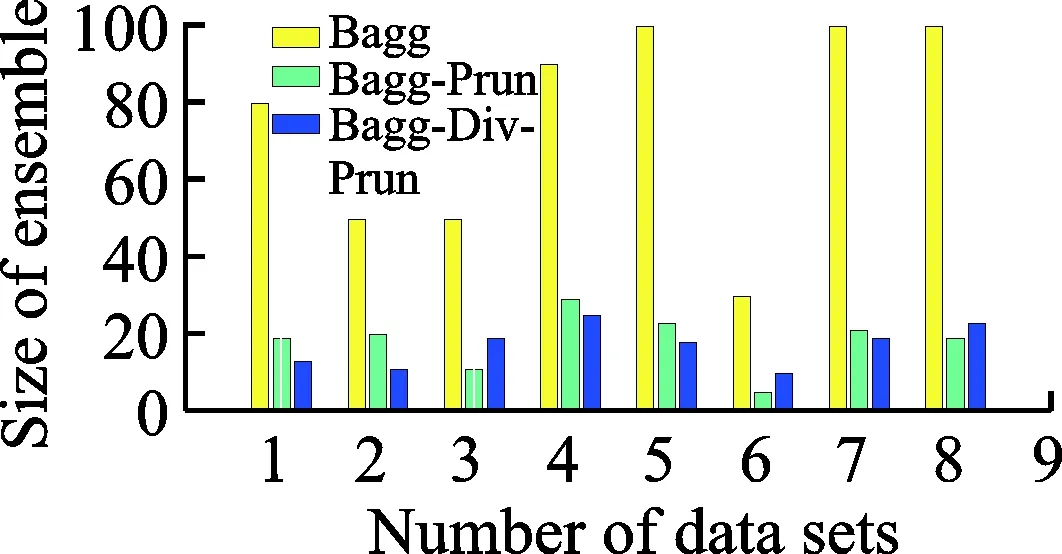
图4 基于C4.5的不同集成剪枝方法集成规模

图5 融入不一致度量后Bagg-Div-Prun, Bagg-Prun的差异性

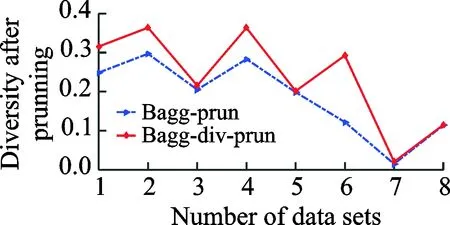
图6 融入熵度量后Bagg-Div-Prun, Bagg-Prun的差异性

3 结束语

集成剪枝方法一般以获得高泛化性能和低集成规模为目标，传统的集成剪枝根据某种数学变换将泛化性能和集成规模转化为一个待优化目标。该方法虽然可以改善集成学习的泛化性能，但是与集成剪枝的初衷有所偏离。目前，研究者们根据经济学原理中的Pareto思想提出了采用双目标优化的方法解决分类器的子集筛选问题。该方法更加直观地解决原始问题，而不是将原问题转化。本文提出的融入差异性的集成剪枝方法是基于Pareto集成剪枝的思想，并在原双目标的基础上增加了一个目标即分类器间的差异性。多个角度剪枝，不仅考虑了分类器的分类准确率、集成规模，还考虑了分类器之间的差异性对集成系统的影响。该过程的优势展现在：(1)融入差异性的Pareto集成剪枝策略确实比没有融入差异性的Pareto集成剪枝策略更优；(2)融入差异性的剪枝策略在泛化性能上的优势来自于差异性，具有相当规模的集成分类器个数时，融入差异性的剪枝策略比没有融入差异性的剪枝策略的泛化性能高。此外，将该融入差异性的集成剪枝策略应用于更多的分类器以及多标签问题中是一个值得研究的方向。

参考文献:

[1] Dietterich T G. Machine learning research[J].AI Magazine, 1997, 18(4): 97.

[2] Dietterich T G. Ensemble methods in machine learning[C]∥Multiple Classifier Systems. Springer Berlin Heidelberg:[s.n.], 2000: 1-15.

[3] Yu Shixin. Feature selection and classifier ensembles: A study on hyperspectral remote sensing data[D]. Antwerpen, Belgi⊇:Universiteit Antwerpen, 2003.

[4] Wolpert D H. Stacked generalization, neural networks[M]. Oxford, UK: Pergamon Press, 1992: 241-259.

[5] Ricardo V, Youssef D.A perspective view and survey of meta-learning[J]. Artificial Intelligence Review, 2002, 18(2):77-95.

[6] Zhou Zhihua, Wu Jianxin, Tang Wei, et al. Ensembling neural networks: Many could be better than all[J].Artif Intell, 2002,(137):239-263.

[7] Tsoumakas G, Partalas I, Vlahavas I. An ensemble pruning primer[C]//Applications of Supervised and Unsupervised Ensemble Methods. Berlin, Heidelberg:Springer,2009: 1-13.

[8] 张春霞,张讲社. 选择性集成学习算法综述[J]. 计算机学报, 2011, 34(8): 1399-1410.

Zhang Chunxia, Zhang Jiangshe. A survey of selective ensemble learning algorithms[J]. Chinese Journal of Computers, 2011, 34(8): 1399-1410.

[9] Li Kai,Huang Houkuan,Ye Xiuchen, et al. A selective approach to neural network ensemble based on clustering technology//Procof the International Conference on Machine Learning and Cybernetics.Banff,Canada:[s.n.], 2004: 3229-3233.

[10] Zhou Z H, Tang W. Selective ensemble of decision trees[C]//Rough Sets, Fuzzy Sets, Data Mining, and Granular Computing. Berlin, Heidelberg:Springer, 2003: 476-483.

[11] Kim M J, Kang D K. Classifiers selection in ensembles using genetic algorithms for bankruptcy prediction[J]. Expert Systems with Applications, 2012, 39(10): 9308-9314.

[12] Zhang Y,Burer S, Street W N. Ensemble pruning via semi-definite programming[J]. The Journal of Machine Learning Research, 2006, 7: 1315-1338.

[13] Partalas I, Tsoumakas G, Vlahavas I. A study on greedy algorithms for ensemble pruning[R]. Technical Report TR-LPIS-360-12, Department of Informatics. Aristotle University of Thessaloniki, Greece, 2012.

[14] Tsoumakas G, Angelis L, Vlahavas I. Selective fusion of heterogeneous classifiers[J]. Intelligent Data Analysis, 2005, 9(6): 511-525.

[15] Partalas I, Tsoumakas G, Vlahavas I. Pruning an ensemble of classifiers via reinforcement learning[J]. Neurocomputing, 2009, 72(7): 1900-1909.

[16] Castro Pablo A, Dalbem d, et al. Designing ensembles of fuzzy classification systems: An immune-inspired approach[C]∥Proceedings of the 4th International Conference on Artificial Immune System. Berlin, Heidelberg:Springer,2005:469-482.

[17] Qian C, Yu Y, Zhou Z H. Pareto ensemble pruning[C]//Proceedings of the 29th AAAI Conference on Artificial Intelligence. Austin, Texas, Palo Alto,USA:AAAI Press,2015:2935-2941.

[18] Kuncheva, L I, Christopher J W. Measures of diversity in classifier ensembles and their relationship with the ensemble accuracy[J].Machine Learning,2003, 51: 181-207.

[19] Breiman L. Bagging predictors[J]. Machine Learning, 1996, 24(2): 123-140.

[20] Friedman J, Hastie T,Tibshirani R. Additive logistic regression: A statistical view of boosting (with discussion and a rejoinder by the authors)[J]. The Annals of Statistics, 2000, 28(2): 337-407.

[21] Zhang Y,Burer S, Street W N. Ensemble pruning via semi-definite programming[J]. The Journal of Machine Learning Research, 2006, 7: 1315-1338.

[22] Ali K M,Pazzani M J. On the link between error correlation and error reduction in decision tree ensembles[M]. Irvine: University of California, 1995.

[23] Yin X C, Huang K, Yang C, et al. Convex ensemble learning withsparsity and diversity[J]. Information Fusion, 2014, 20: 49-59.

[24] Kuncheva L I, Christopher J W. Measures of diversity in classifier ensembles and their relationship with the ensemble accuracy[J].Machine Learning, 2003,51: 181-207.

[25] Liao Y,Vemuri V R. Use of k-nearest neighbor classifier for intrusion detection[J]. Computers & Security, 2002, 21(5): 439-448.

[26] Friedl M A, Brodley C E. Decision tree classification of land cover from remotely sensed data[J]. Remote Sensing of Environment, 1997, 61(3): 399-409.