基于置信规则库推理的二择众仓分类方法
方志坚 傅仰耿 陈建华
(福州大学数学与计算机科学学院,福州, 350116)
引 言
随着互联网络及媒体设备的高速发展,各个行业领域每时每刻均在产生大量的数据。数据信息量的激增导致了海量数据库的产生,如何在海量信息源中提取隐藏和有价值的信息,并应用这些信息构建决策支持的模型一直在商务管理、生产控制和市场分析等领域有着强烈的需求。因此数据挖掘如今成为一个热门的研究领域。数据分类是数据挖掘领域中一个重要的分支,这是由于大多数的实际工程问题均能转换成分类问题。分类就是利用已知标签的数据来构建相关的模型,进而确定未知类别数据标签的决策过程。
目前已经有许多经典的分类算法被提出,例如:K近邻[1]、支持向量机[2]和粗糙集[3]等方法。K近邻算法原理相对简单,方法易于实现,并且支持增量学习,具有对复杂决策空间进行建模的能力,其缺点在于寻找近邻点需要大量的计算,且当数据中包含弱相关属性时,其分类精度会下降;支持向量机在已知核函数的情况下,能够大大减少对高维问题的求解复杂度,其在一定程度上具有泛化推广的能力,因此也导致了支持向量机的分类精度十分依赖核函数的选择,而如何选择核函数一直是一个公认的难题;粗糙集的优点在于不需要附加信息或先验知识,就能够处理存在不精确乃至不完整数据的问题。但它只能处理离散化的属性,且产生的决策规则不稳定,准确率有待提高。
置信规则库推理方法(Belief rule-base inference methodology using evidential reasoning approach, RIMER)最早由Yang等[4]提出,囊括了传统IF-THEN规则库[5]、D-S证据理论[6,7]、决策理论[8]和模糊理论[9]等方面的知识,具有对不完整或不精确信息进行建模的能力。当前,以RIMER为核心的置信规则库(Belief rule base,BRB)系统已经广泛应用于输油管道检漏[10]、工程系统安全评估[11]和军事能力评估[12]等工程领域。传统的RIMER方法不适用于属性数量过多的问题,这是由于BRB在构建过程中需要遍历所有前件属性的各个候选值,因此随着属性数量的增多,BRB的规则条数将呈指数级增长,这必然会导致“组合爆炸”问题的产生。鉴于此,前人提出了通过线性组合的方式构建规则库,使得规则库的条数不再随属性数量的增长而增长。由于规则库在结构上发生了改变,使得原有方法中的激活公式不再适用于现有方法。因此,Chang等[13]将原有方法中的激活规则改为激活属性,即不再关注哪条规则被激活,而是注重前件属性的哪些候选值被激活。将BRB应用于分类算法中,Ye等[14]提出设定规则数等于分类数,以输入值和候选值之间距离倒数的归一化值作为个体匹配度,即对于任何输入值,规则库中的每条规则都将被激活,激活权重表现为每条规则对分类结果的贡献度。这些方法不仅解决了“组合爆炸”问题,而且在分类准确性上获得了不错的效果。然而采用线性组合方式也存在两点不足:(1)线性组合迫使每个前件属性候选值的个数必须相等,这也就忽略了各个前件属性间的差异;(2)激活权重公式的改变导致后件置信度受到了来自非激活前件属性候选值的影响,即在原始RIMER方法中,参与证据推理(Evidertail reasoning, ER)合成的置信度所对应规则的候选值都存在个体匹配度,而采用线性组合的方式,常常出现个体匹配度为0的属性参与激活合成,这必然会影响后件置信度。
本文提出一种改进置信规则库推理的分类方法。首先,在文献[13]研究的基础上,将评价等级个数设定为两个,即后件评价等级个数不再等于分类数。对于一组输入值,RIMER过程只得出该输入值是否满足某种特定条件,以及以多大的置信度满足该条件。其次,对于某一具体问题不再局限于设定一个规则库,而是同时存在多个规则库进行决策。依据数据的特性,采用One-versus-One和有向无环图来构建决策模型。最后,再根据各个规则库的决策结果进行类别“投票”,票数最高的即为最终分类结果。
1 置信规则库推理方法
采用规则形式表示相关信息在人工智能领域是一种非常常见的方式,在置信规则库推理方法中,规则化的信息表示体现在了置信规则库中。
1.1 置信规则库表示
置信规则库由传统IF-THEN规则库演化而来,Yang等将置信框架引入IF-THEN规则中,使得传统的IF-THEN规则能够合理地表示不完整或不确定信息的知识,从而提出新的规则表达式。新的规则即称为置信规则,其中第k条置信规则可表示为

(1)
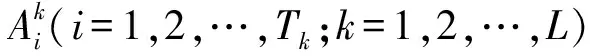
1.2 置信规则库系统推理过程
BRB系统的规则推理由计算激活权重、修正后件置信度和合成激活规则3步组成。在计算激活权重前,需先计算各个前件属性候选值的个体匹配度,计算方法为
(2)
其中,输入值向量表示为x={x1,x2,…,xT}。
第k条规则激活权重的计算公式为
(3)

(4)
式中:Ut表示第k条规则的第t个前件属性;Rk表示第k条规则的前件属性集合。
由激活规则的后件置信度和激活权重可以求得基本属性的基本可信值为
mj,k=ωkβj,k
(5)

(6)
(7)

最后将激活的规则使用ER法则合成,得到相对于评价等级Dj的基本可信度分配值,即
(8)
(9)
(10)
(11)
(12)
(13)
1.3 参数学习模型

图1 BRB参数训练模型Fig.1 BRB parameter training model
专家根据历史信息和先验知识给定的初始BRB系统存在主观局限性,特别是当BRB系统应用于复杂决策问题时,人为方式难以精确地给出这些参数值。故Yang等[15]提出了BRB系统参数训练模型,通过比较观测输出和推导输出的差值来矫正BRB系统的参数,进而提高RIMER方法决策的准确性。训练模型如图1所示。参数优化模型可表示为
min{Δ(P)}
s.t.A(P)=0,B(P)≥0
(14)
式中:p=(βi,k,θk,δk,i)为待训练的参数向量;Δ(P)为目标函数,当Δ(P)越小时,表明该BRB系统更符合实际系统,故最小化Δ(P)是参数训练的最终目的;A(P)和B(P)分别是等式和不等式约束条件。在参数训练过程中,文献[15]给出如下规定
(15)
(2) 标准化规则权重θk,使其不小于0且不大于1,即
0≤θk≤1k=1,2,…,L
(16)
(3) 任意一条置信规则的后件置信度均不小于0且不大于1,其中第k条规则的第j个评价等级上的置信度需满足
0≤βj,k≤1j=1,2,…,N;k=1,2,…,L
(17)
(4) 假设第k条规则是完整的,即输入不包含不确定或模糊信息,则该条规则的后件置信度之和等于1,即
(18)
2 现有置信规则库推理的分类方法
目前,置信规则库推理方法应用于分类已经在淋巴结疾病诊断[16]和UCI分类数据集的测试[17]上取得了一定的进展。采用置信规则库推理方法解决分类问题主要有以下两种构建规则库策略。
(1)采用遍历前件属性候选值的方式,无需改变原始BRB系统,在处理分类问题时,只需要将后件置信度转换成分类结果信息,即可直接将RIMER方法应用到分类问题中。然而该方法只能应用于数据属性数目较少的情况,这是由于遍历组合方式继承了传统RIMER方法中固有的“组合爆炸”问题。随着数据属性数目的增多,规则库的条数将呈指数级增长。以数据集Wine为例,其数据属性个数有13个,假设每个前件属性候选值的个数均为3个,那么BRB的规则条数就达到了313条,此时参数训练所耗费的时间是令人无法忍受的。通过遍历组合方式构建的规则库大小可表示为
(19)
其中Tk表示第k个前件属性候选值的个数。通过对UCI上210组分类数据进行统计后发现,前件属性个数小于10的分类数据集个数仅为54组,而属性个数大于10的有156组,由此可知分类数据通常为多属性的情况。因此采用遍历组合方式构建规则库并不适用于大部分的分类问题。
(2)采用线性组合方式构建置信规则库中的规则。例如,有3个前件属性,每个前件属性的候选值依次为:{1,2,3},{4,5,6}和{7,8,9},则通过线性组合方式构建的置信规则库为
R1:ifA1is 1∧A2is 4∧A3is 7,then{D}
R2:ifA1is 2∧A2is 5∧A3is 8,then{D}
R3:ifA1is 3∧A2is 6∧A3is 9,then{D}
(20)
可以看出,采用线性组合的方式,规则库中规则的条数只与前件属性候选值的个数有关,而与前件属性个数无关,这样就有效避免了“组合爆炸”问题的产生。然而,采用线性组合方式构建的置信规则库中常常会出现“零激活”问题,这是由于在计算个体匹配度时,至多仅有两个候选值的个体匹配度非零,其余的皆为零。根据式(3)可知,只要规则中存在某个前件属性候选值的个体匹配度为零,那么该条规则的激活权重就为零,即不被激活。因此,激活权重公式可修正为
(21)
即将个体匹配度的累乘形式改为累加形式,这样激活条件变为了只要规则中某个属性候选值的个体匹配度不为零,那么该条规则就会被激活。
采用线性组合方式构建的BRB分类方法在一定程度上已能有效地解决分类问题,然而由于线性组合的方式也暴露出以下两点不足:
(1)线性组合的方式迫使每个前件属性候选值的个数必须相等,这样就忽略了各个前件属性间的差异。在原始BRB规则库中,各个前件属性候选值个数一般不相等,其个数往往取决于该属性值的区间大小以及所占的权重比例,通常情况下,区间越大,比重越大,则候选值的个数也就越多。文献[13]所提出的方法中,前件属性权重已从激活规则公式中删去,也就是说,该方法认为各个前件属性同等重要,这往往不可取,因为这样会夸大弱属性的效用,而弱化了强属性的分类支持度,导致最终的分类准确性下降。
(2)激活权重公式的改变导致了后件置信度受到了来自非激活前件属性候选值的影响。即原始方法中,参与ER合成的置信度,其所对应规则的候选值都存在个体匹配度。从修正后的激活权重公式来看,规则中存在某个属性候选值的个体匹配度不为零,那么该条规则所携带的信息就会参与ER合成。倘若只有一个候选值的个体匹配度不为零,那么完全可以弱化该条规则对结果所占比重的影响。特别是当该激活点属于噪音情况时,肯定会对结果造成不利的影响,使得最终的分类准确性下降。从式(8~13)的计算过程可以看出,随着后件评价等级个数的增加,该缺点所带来的影响也会随之增大。
3 基于二择众仓的置信规则库推理的分类方法
针对现有置信规则库推理分类方法的不足,本文提出一种二择众仓决策法。对原有的方法作如下改进:
(1)将规则表达式修正为

(22)
即每条规则仅设计两个评价等级,置信规则库的推理结果只对输入值作出是与否的置信决策,而不再作多值判定,仅仅是在二者间选择。其好处是规则变得简单,在处理信息时更加快捷高效,而且该设计策略能够很好地改善第2节中所提到的第2点不足,从而使得分类准确性有所提高。
(2)引入众仓决策模型。在对规则表达式作出修正后可以很明显地看出由于后件评价等级个数只有两个,那么由此类规则所构建的置信规则库只能对二分类问题做出判定,而无法解决多分类问题。因此本文创新性地提出采用多规则库的方式解决同一个分类问题,即每一个置信规则库都是一个二分类决策器,而由多个二分类决策器构成了众仓决策模型,进而解决多分类问题。采用众仓模型后,每一个置信规则库只关心两个类别间或两个大类别间的差异,此时每一个置信规则库都可以有自己的前件属性权重值。例如:存在一个4属性、3类别的分类数据集,可以在两两类别间设置一个置信规则库,假设区分1,2类别仅需要前两个属性,那么对于第1个置信规则库完全可以将3,4属性的权重值设置为零。该优点是现有置信规则库分类方法所不能拥有的,只有一个置信规则库的分类方法,其前件属性权重必须同时考虑区别1,2,3类。因此,采用众仓决策模型可以很好地解决第2节中所提到的第1点不足。
图2给出了三类别示例。如图所示,在类别1与类别2间、类别1与类别3间找到一个可分平面十分容易,然而在类别2与类别3间找到一个可分平面就相对比较困难,采用现有的分类方法无法直接了断地解决该瓶颈,只能通过增加规则条数或参数训练复杂度的方法来解决,这必然会对类别1产生影响。若是采用二择众仓决策法,类别1与类别2间、类别1与类别3间的分类器在训练过程中可以很快地获得精准结果,而对于类别2与类别3间的分类器,在训练过程中就可以发现这是整个分类问题的瓶颈,这样就不再是“黑箱”操作,而是清楚明了地知道问题瓶颈所在的位置,此时可以通过增加规则条数或增加参数训练复杂度的方法来解决,同时对类别1不会造成任何影响。这也是二择众仓决策法的优点之一。

图2 三类别示例Fig.2 Illustraction example of three categories
二择众仓决策法不改变RIMER方法的整个体系结构,单个置信规则库的所有操作都与原来一致,改变的只是评价等级个数,也就是让单个置信规则库只解决一个小问题,将处理结果返回给该体系外的众仓决策模型,该模型将多个小问题的结果进行融合,从而解决问题。这样不仅继承了原有RIMER方法中的优点,而且在一定程度上改善了由线性组合方式所带来的不足。二择众仓决策法的具体实现步骤为
(1)依据数据的特性选择合适的众仓决策模型。以Glass数据集为例,通过查看其类别描述可获得如下信息:
Class Distribution: (out of 214 total instances)
——163 Window glass (building windows and vehicle windows)
-- 87 float processed
-- 70 building windows
-- 17 vehicle windows
-- 76 non-float processed
-- 76 building windows
-- 0 vehicle windows
-- 51 Non-window glass
-- 13 containers
-- 9 tableware
-- 29 headlamps
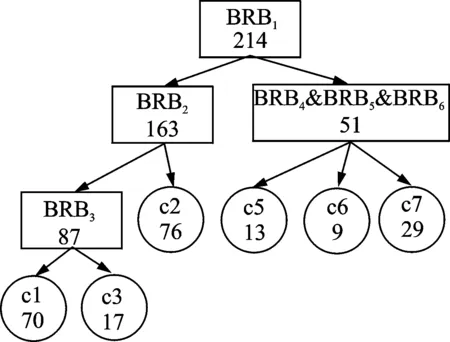
图3 Glass数据集的众仓决策模型Fig.3 Multiply decision-making model of Glass dataset
可以看出Glass数据集的类别结构层次分明,能很容易地采用有向无环图来构建众仓决策模型,如图3所示。Glass数据集中类别4的个数为零,故未在图中标出。从图3可以看出,对Glass数据集进行分类需要设计6个BRB分类器,其中BRB1用来区分Window glass与Non-window glass这两类,Window glass有4个类别标签:1,2,3和4,Non-window有3个类别标签:5,6和7。即BRB1是区分1,2,3,4类和5,6,7类的分类器。BRB2,BRB3和BRB1同理不再赘述。BRB4,BRB5和BRB6采用One-versus-one算法,即在两两类间训练一个分类器,当对一个未知样本进行分类时,每个分类器都对其进行判定,并给相应的类别“投上一票”,最后票数最多的类别作为该样本的类别。该步骤可用图4所示的流程图表示。
(2)由于各个分类器在训练的过程中相互不存在影响,可以采用并行的策略同时进行训练。训练的过程中发现有瓶颈问题,可以不断调整训练参数,以获得更加满意的结果。本文中的实验均采用差分进化算法对BRB的参数进行训练。以均方差(Mean squared error, MSE)作为参数训练模型中的目标函数,即
(23)

(3)后件置信度转换成类别信息。由于后件评价等级只有两个,将两个评价等级与两个分类级别对应起来,则最终的分类结果为
(24)
其中i,j表示类别的编号。
4 实验分析与结果对比
通过实验将二择众仓决策法与现有的分类方法进行对比,以差分进化算法作为参数训练的优化算法。一般情况下将种群规模设置在50,交叉概率为0.9,缩放因子为0.5。实验环境为:Intel(R)Core(TM)i5-4570 CPU @3.20 GHz处理器,8 GB内存,Windows7操作系统。程序均在Matlab2014b中实现。
4.1 实验1
本实验所使用的3个数据集均来自UCI公共测试集,分别为:Iris,Wine和Glass。表1显示了3个测试数据集的基本信息。

表1 数据集基本信息
采用十折交叉验证法,即将样本数据分成10份,每次取其中的1份作为测试集,其余的作为训练集。十折交叉验证法的实验结果如表2所示。
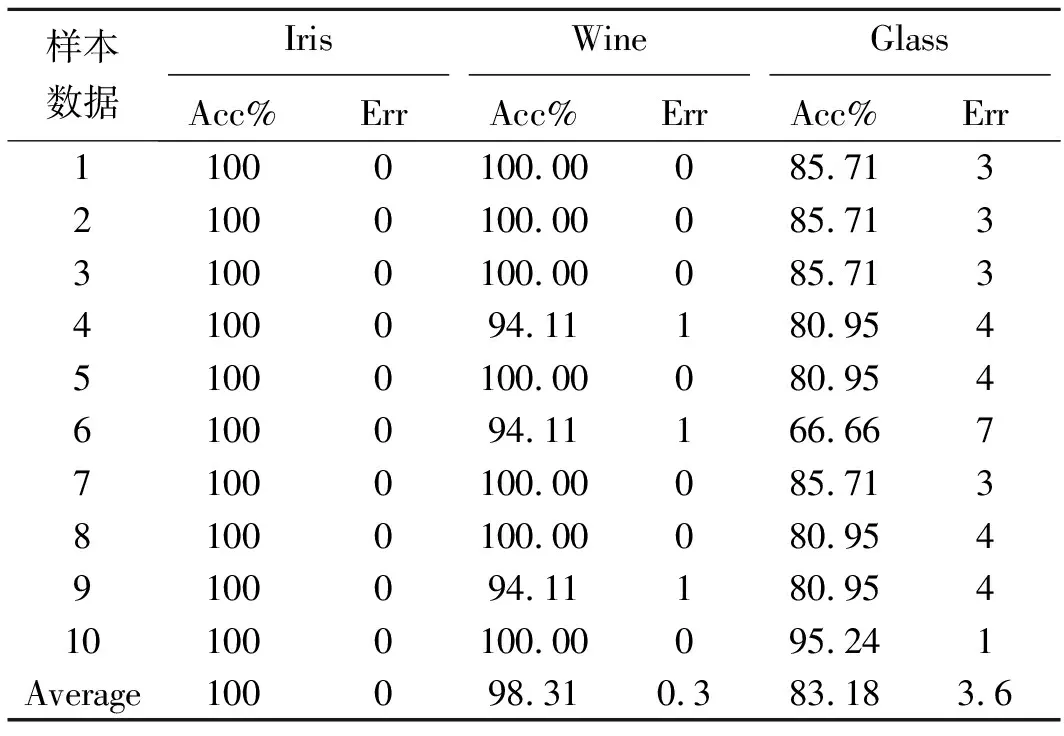
表2 十折交叉验证结果
为了进一步验证本文方法的有效性,将本文方法与文献[13,14]同样是采用置信规则库推理的分类方法进行对比,并选取近两年来对这3个数据集进行分类的其他方法进行对比,对比结果如表3和图5~7所示。

表3 不同方法在不同数据集上的分类准确率对比

图5 Iris数据集的各方法分类准确率对比 图6 Wine数据集的各方法分类准确率对比
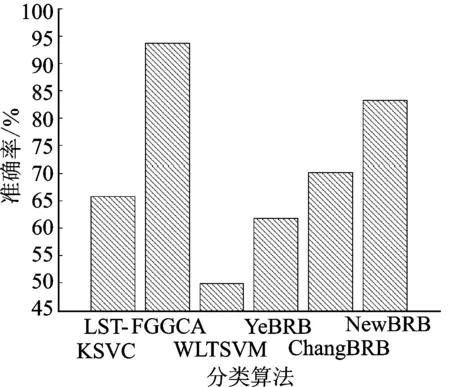
图7 Glass数据集的各方法分类准确率对比 Fig.7 Classification accuracy contrast by using different methods on Glass dataset
将本文方法与非BRB方法进行对比,可以看出除了FGGCA的Glass数据集外,余下结果都不如本文的方法来得更优。将本文方法与文献[13,14]的方法进行对比,文献[14]的实验缺失Wine数据集的结果,然而从Iris和Glass数据集来看,其结果均不如本文的方法好。而对比文献[13]方法,在Glass数据上本文的方法有了很大的提升,这是由于Glass数据集带有二分类的特性,特别适用于本文提出的方法。没有任何一种方法能对所有数据集均达到最优的结果,但纵观全局来看,本文的方法在一定程度上提升了分类的准确性。
4.2 实验2
本实验在于说明文献[13]提出的方法随着类别个数的增多,其分类准确率将会急剧下降。而采用二择众仓决策方法,将会大幅度地减少准确率的下降程度。实验数据样本来源于Brodatz库中的14幅纹理图像,其在Brodatz库中的编号分别为D1,D6,D12,D15,D20,D34,D37,D52,D56,D65,D72,D87,D93和D110,具体如图8所示。

图8 Brodatz库中的14幅纹理图像Fig.8 Fourteen texture images from Brodatz library
这14幅纹理图像原始大小均为640像素×640像素,将每幅图像不重叠地切割成4×4=16幅子图,每幅子图大小均为160像素×160像素,共获得14×16=224幅样本图像。选取每幅图像的前8幅子图作为训练数据,后8幅子图作为测试数据。使用Matlab2014b所提供的graycomatrix和graycoprops函数获取每幅子图的灰度共生矩阵特征值,并以此作为分类依据。实验类别个数从初始的4个逐步增加至14个。实验结果如图9所示。

图9 实验结果对比Fig.9 Experimental results comparison
从实验结果可以看出,在类别个数较少时,文献[13]方法与二择众仓决策方法差别不大。但随着类别个数的增多,其准确率会急剧下降,对14幅纹理图像同时进行分类时其准确率仅有30.36%。这是由于线性组合方式并不适用于类别个数较多的情况,这已在第2节中做了详细说明。而采用二择众仓决策方法后会大幅度地减少该不足所带来的影响,对14幅纹理图像同时进行分类时依然能保持较高的准确率,说明本文所提出的方法具有较强的鲁棒性。
5 结束语
虽然通过线性组合方式构建置信规则库避免了规则条数随着问题属性数量的增多而激增,但该方式仍然存在不足。鉴于此,本文提出一种改进置信规则库推理的分类方法,首先将一个大的分类问题切割成若干个相对独立的分类小问题,每个小问题都是一个二分类问题;其次将规则的后件评价等级设置为两个让每个置信规则库只处理一个小问题,以此减小线性组合所来的的误差;最后,采用众仓决策的方式将若干个小问题的结果进行整合,从而得出最终的分类结果,通过实验分析验证了该方法的可行性。本文在现有置信规则库推理分类算法的基础上,通过改进分类器的设计,从而进一步提高了分类准确率。如何处理类别数量更多的分类问题将是下一步研究的方向。
参考文献:
[1] Cover T,Hart P.Nearest neighbor pattern classification[J].IEEE Transactions on Information Theory,1967,13(1):21-27.
[2] Cortes C,Vapnik V.Support-vector networks[J].Machine Learning,1995,20(3):273-297.
[3] Bazan J G,Nguyen H S,Nguyen S H,et al.Rough set algorithms in classification problem[J].Rough Set Methods and Applications,2000,56(1):49-88.
[4] Yang Jianbo,Liu Jun,Wang Jin,et al.Belief rule-base inference methodology using the evidential reasoning approach-RIMER[J].IEEE Transactions on Systems, Man and Cybernetics,Part A:Systems and Humans,2006,36(2):266-285.
[5] Sun R.Robust reasoning:Integrating rule-based and similarity-based reasoning[J].Artificial Intelligence,1995,75(2):241-295.
[6] Dempster A P.A generalization of Bayesian inference[J].Journal of the Royal Statistical Society,1968,30(2):205-247.
[7] Shafer G.A mathematical theory of evidence[M].Princeton: Princeton University Press,1976:10-39.
[8] Hwang C L,Yoon K.Methods for multiple attribute decision making[M].[S.l.]: Sringer Berlin Heidelberg,981:58-191.
[9] Zadeh L A.Fuzzy sets[J].Information and Control,1965,8(3):338-353.
[10] 周志杰,杨剑波,胡昌华,等.置信规则库专家系统与复杂系统建模[M].北京:科学出版社,2011:9-41.
Zhou Zhijie,Yang Jianbo,Hu Changhua,et al.Belief rule base of expert system and complex system modeling[M].Beijing:Science Press,2011:9-41.
[11] Liu Jun,Yang Jianbo Ruan Da,et al.Self-tuning of fuzzy belief rule bases for engineering system safety analysis[J].Annals of Operations Research,2008,163(1):143-168.
[12] Jiang Jiang,Li Xuan,Zhou Zhijie,et al.Weapon system capability assessment under uncertainty based on the evidential reasoning approach[J].Expert Systems with Applications,2011,38(11):13773-13784.
[13] Chang Leilei,Zhou Zhijie,You Yuan,et al.Belief rule based expert system for classification problems with new rule activation and weight calculation procedures[J].Information Sciences,2016,336(1):75-91.
[14] 叶青青,杨隆浩,傅仰耿.基于改进置信规则库推理的分类方法[J].计算机科学与探索,2016,10(5):709-721.
Ye Qingqing,Yang Longhao,Fu Yanggeng.Classification approach based on improved belief rule-base reasoning[J].Computer Science and Technology,2016,10(5):709-721.
[15] Yang Jianbo,Liu Jun,Xu Dongling,et al.Optimization models for training belief-rule-based systems[J].IEEE Transactions on Systems,Man,and Cybernetics,Part A:Systems and Humans,2007,37(4):569-585.
[16] Zhou Zhiguo, Liu Fang,Jiao Licheng,et al.A bi-level belief rule based decision support system for diagnosis of lymph node metastasis in gastric cancer[J].Knowledge-Based Systems,2013,54:128-136.
[17] Calzada A,Liu J,Wang H,et al.A new dynamic rule activation method for extended belief rule-based systems[J].IEEE Transactions on Knowledge and Data Engineering,2015,27(4):880-894.
[18] Nie Qingfeng,Jin Lizou,Fei Shumin,et al.Neural network for multi-class classification by boosting composite stumps[J].Neurocomputing,2015,149:949-956.
[19] Sanchez M A,Castillo O,Castro J R,et al.Fuzzy granular gravitational clustering algorithm for multivariate data[J].Information Sciences,2014,279:498-511.
[20] Shao Yuanhai,Chen Weijie,Wang Zhen,et al.Weighted linear loss twin support vector machine for large-scale classification[J].Knowledge-Based Systems,2015,73:276-288.

