利用粒子流滤波的单通道BPSK信号盲分离算法

赵知劲 吴 棫

(杭州电子科技大学通信工程学院,杭州,310018)

引 言

单通道信号盲分离在图像、通信和语音等方面具有广泛的实际应用前景，近年来越来越受到研究者关注，逐渐成为信号处理领域的一个研究热点[1]。单通道信号盲分离是欠定信号盲分离的一种特殊情况，即在只有一个观测信号的情况下实现对若干个源信号的分离。由于只有一个观测信号，所以传统的多通道信号盲分离方法不能直接应用于单通道信号盲分离。

单通道信号盲分离是一个极具挑战性的问题，目前还没有一个普遍适用于分离各种不同混合信号的算法，现有的单通盲道分离算法都针对不同信号各自的特点提出。关于通信信号单通道盲分离，不同信号分离方法的实质都是利用混合信号之间存在的差异(比如信号在符号速率、功率和时频域等上的差异)来实现对源信号的分离。文献[2]中的小波变换法利用两路数字信号之间存在符号速率上的差异实现信号分离，但是该方法只有当源信号之间存在较为显著符号速率差异并且不考虑额外信道噪声情况时才能实现对源信号的分离。文献[3]利用信号结构上的稀疏性实现对源信号的分离，但是这种方法要求保证两路源信号基本同步，并且需要较高的信噪比。文献[4]利用成型滤波器之间的差异，提出利用过采样从单通道接收信号获得多路信号，从而将高度欠定的单通道盲分离问题转换为适定的盲分离问题，然后再利用独立分量分析算法分离源信号，但是当成形滤波器之间差异较小、系统存在相偏以及频偏等非线性因素时，这种算法分离效果较差。文献[5]将信号盲分离问题转换为状态估计问题，将粒子滤波应用于源信号的符号序列和参数估计，获得了较好的源信号分离性能，但是粒子滤波本身存在的“粒子贫化”[6]现象容易导致分离性能恶化和过高的计算复杂度，从而影响该方法的实际应用效果。文献[7]在粒子滤波基础上引入遗传算法来迭代估计优质粒子，从单通道接收信号中分离出一路通信信号与干扰。本文提出一种基于粒子流滤波(Particle flow filter, PFF)的单通道信号盲分离算法。通过改变粒子的更新方式，避免了粒子滤波中“粒子贫化”现象的发生，获得了更好的误码率性能，并且降低了计算复杂度。

1 信号模型

假设接收端得到的单通道信号是由两路同频BPSK基带源信号混合，接收信号表示为

y(t)=z1(t)+z2(t)+v(t)

(1)

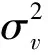
(2)

式中：ζ1和ζ2分别为两路源信道各自的传输衰落；Δf1和Δf2为两路源信号的残余频偏；φ1和φ2为两路源信号各自的初始相位；an和bn为具有相同星座图的两路BPSK源信号传输的码元；T为符号周期，τ1和τ2为两路源信号对应的定时偏差，τ1,τ2的取值范围为[-T/2,T/2]；gi(t)(i=1,2)是滚降系数为αi的升余弦滚降滤波器，可以表示为

(3)

其中0<αi<1。假设z1(t)和z2(t)与v(t)相互统计独立，升余弦滚降滤波器持续时间有限，在接收端按符号速率1/T对y(t)进行采样，得到接收信号的离散形式为

(4)

(5)

根据式(5)单通道盲信号分离问题可以描述为：在未知或者仅知道参数θ部分信息的情况下，利用单通道信号yk对两路源信号的符号序列ak和bk进行估计，从而实现两路源信号的分离。

两路源信号符号序列的状态方程可表示为

(6)

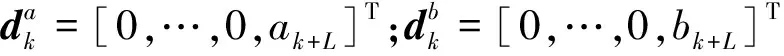
(7)

假设未知参数向量θ在迭代过程中固定不变，其状态方程可以表示为

θk=θk-1

(8)

由此得到了状态空间的状态方程如式(6～8)所示，测量方程如式(5)所示。

2 基于PFF的单通道BPSK信号盲分离算法

2.1 粒子流滤波

将待估计未知信号的符号序列和参数的集合表示为xk={ak,bk,θk}，根据贝叶斯公式可以得到关于xk的k时刻状态后验分布,即

(9)

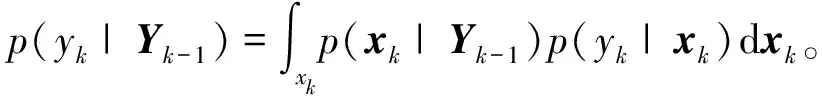
粒子滤波直接通过式(9)中函数的点乘实现贝叶斯滤波,而粒子流滤波[8]的基本思想则是通过建立一个微分方程将状态空间中服从先验分布的粒子移动到其对应的后验分布上，从而实现贝叶斯滤波。

为了便于表示，将式(9)中的函数表示如下：q(x)=p(xk|Yk)，g(x)=p(xk|Yk-1)，l(x)=p(yk|xk)，K(x)=p(yk|Yk-1)，式(9)可示为

(10)

对式(10)两边取对数，得

log(q(x))=log(g(x))+log(l(x))-log(K(x))

(11)

引入标量参数λ来扮演类似时间的角色，λ在[0,1]内取值，利用拓扑学中同伦的概念定义一个关于变量λ的对数同伦函数

log(q(x,λ))=log(g(x))+λlog(l(x))-logJ(λ)

(12)

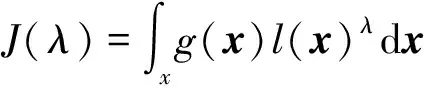
(13)

其中的f(x,λ)为满足Fokker-Planck方程的函数[10]，w为过程噪声。利用Fokker-Planck方程并结合式(12)和式(13)，得到关于f(x,λ)的表达式,有

(14)

式中:Tr(·)表示(·)的迹，Q表示式(13)中过程噪声w的协方差矩阵。为了简化讨论过程，这里令Q=0，于是式(13)和式(14)可分别简化为

(15)

(16)

由于函数q关于λ是光滑且连续的，式(12)两端分别对λ求导得到

(17)

结合式(16)和式(17)可以得到

(18)

其中m(λ)=∂J(λ)/∂λ，式(18)就是式(9)贝叶斯估计所应满足的常微分方程。粒子流滤波利用式(10)取代重采样更新粒子，从而有效避免了粒子滤波中的“粒子贫化”问题。

2.2 基于粒子流滤波的单通道BPSK信号盲分离算法

根据单通道BPSK信号的状态方程式(6～8)和观测方程式(5)，求解式(18)得到f，然后由式(15)积分得到所要估计的x，这就是本文提出的利用粒子流滤波的单通道信号盲分离方法。有多种方法可以求解式(18)[11-13]，文献[13]方法比较简单，更适合于本文问题。该方法首先假设f(x,λ)是无旋的，然后应用Galerkin有限元法[14]和蒙特卡罗积分法，给出了一种易于计算的f(x,λ)的闭集解为

(19)

其中的xi表示样本粒子，xi服从q(x,λ)定义的概率分布。似然函数l(xi)表示为

logl(xi)=(yk-h(xi))TR-1(yk-h(xi))

(20)

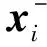
(21)

则状态估计值

(22)

利用式(19～22)即可迭代实现粒子流滤波。综上所述可得，基于粒子流滤波的单通道信号盲分离算法主要步骤如表1所示。

表1中的K为仿真实验采样点数，M=1/Δλ。本文使用欧拉积分法，也可以采用其他数值积分方法。

表1 基于粒子流的单通道信号盲分离算法

3 算法仿真与性能分析

当上述两种算法估计性能相近时且在SNR=30 dB的高斯噪声环境下，对两种算法运行100次所需时间平均值如表2所示。由表2可知，PFF-SBSS算法的计算复杂度低于PF-SBSS算法。

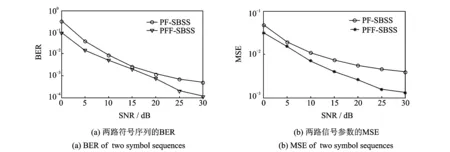
图1 高斯环境噪声下两种算法的BER和MSEFig．1 BER and MSE of two algorithms under Gaussian environmental noise

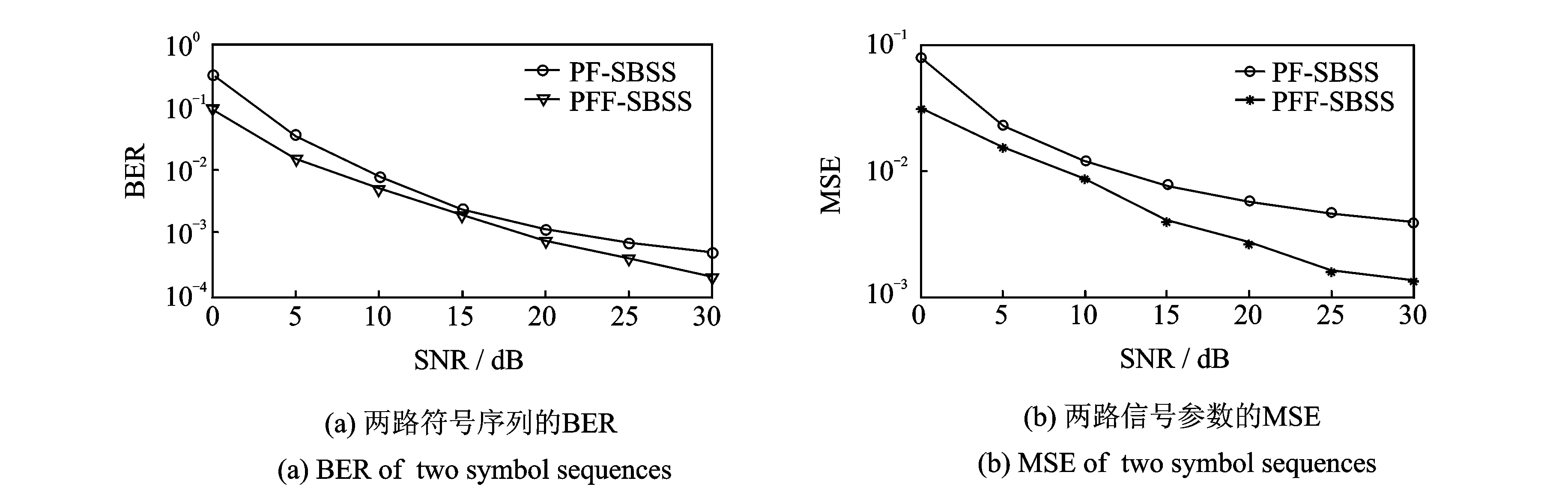
图2 非高斯环境噪声下两种算法的BER和MSEFig．2 BER and MSE of two algorithms under non-Gaussian environmental noise

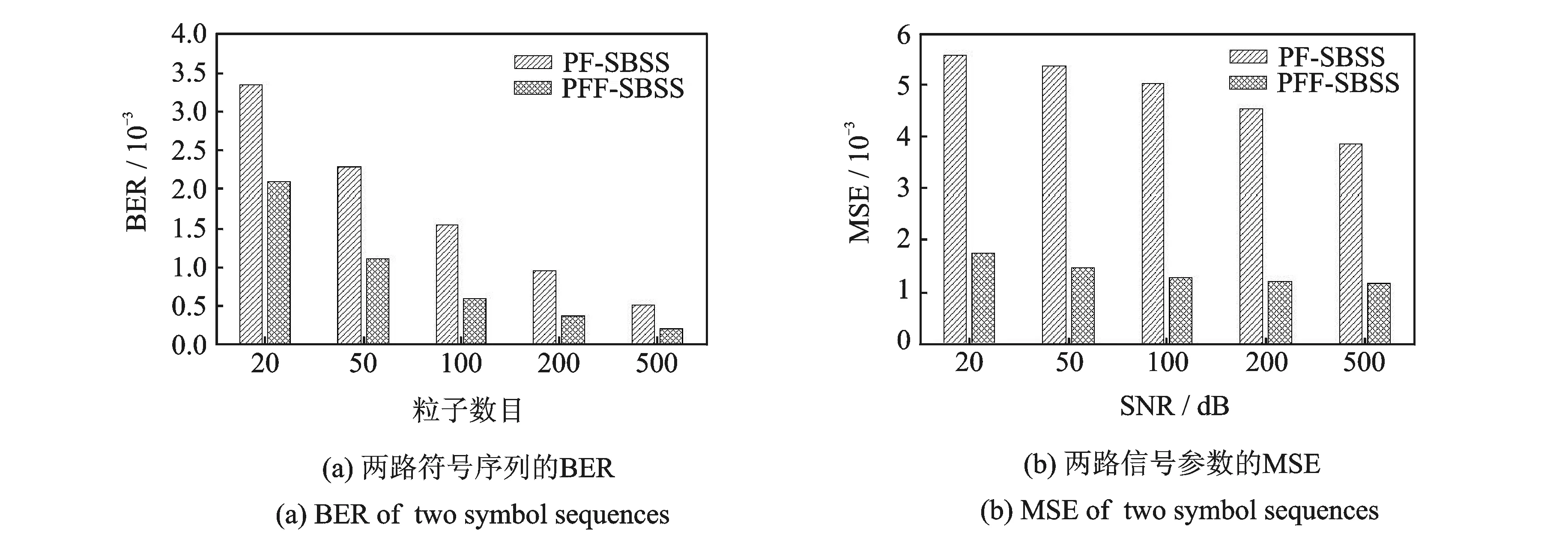
图3 不同粒子数目下两种算法的BER和MSEFig．3 BER and MSE of two algorithms under different particle numbers

表2 两种滤波算法的平均运行时间

4 结束语

本文提出了一种基于粒子流滤波的单通道BPSK信号盲分离方法，首先将BPSK信号的符号序列估计问题建模为状态估计模型，然后利用粒子流滤波进行状态估计。采用粒子流形式更新粒子，有效避免了粒子滤波方法中重采样引起的“粒子贫化”问题，相比基于粒子滤波的单通道BPSK盲分离算法，本文算法估计精度高，计算复杂度低。

参考文献:

[1] Li Y, Amari S I, Cichocki A, et al. Underdetermined blind source separation based on sparse representation[J]. IEEE Transactions on Signal Processing, 2006, 54(2): 423-437.

[2] Heidari S, Nikias C L. Co-channel interference mitigation in the time-scale domain: The CIMTS algorithm[J]. IEEE Transactions on Signal Processing, 1996, 44(9): 2151-2162.

[3] Szu H, Chanyagorn P, Kopriva I. Sparse coding blind source separation through powerline[J]. Neurocomputing, 2002, 48(1): 1015-1020.

[4] Warner E S, Proudler I K. Single-channel blind signal separation of filtered MPSK signals[J]. IEE Proceedings Radar, Sonar and Navigation, 2003, 150(6): 396-402.

[5] Shilong T, Shaohe C, Hui Z, et al. Particle filtering based single-channel blind separation of co-frequency MPSK signals[C]∥ 2007 International Symposium on Intelligent Signal Processing and Communication Systems. Xiamen: IEEE,2007: 582-585.

[6] Daum F, Huang J. Particle degeneracy: Root cause and solution[C] // SPIE Defense, Security, and Sensing. Orlando:SPIE, 2011: 80500W-80500W-11.

[7] 路威,张邦宁，张杭.利用遗传粒子滤波的单通道扰信盲分离算法[J]. 数据采集与处理, 2014, 29(5)：783-789.

Lu Wei, Zhang Bangning, Zhang Hang. Single-channel blind separation of communication signal and interference using genetic particle filtering[J]. Journal of Data Acquisition and Processing, 2014, 29(5)：783-789.

[8] Daum F, Huang J. Particle flow for nonlinear filters, Bayesian decisions and transport[C] ∥ 16th International Conference on Information Fusion. Istanbul: IEEE, 2013: 1072-1079.

[10] Risken H. Fokker-planck equation[M]. Heidelberg: Springer, 1984: 117-174.

[11] Daum F, Huang J. Particle flow with non-zero diffusion for nonlinear filters, Bayesian decisions and transport[C]// Signal and Data Processing of Small Targets.[S.L.]:[s.n.],2013: 1117-1123.

[12] Daum F. Exact finite-dimensional nonlinear filters[J]. IEEE Transactions on Automatic Control,1986, 31(7): 616-622.

[13] 张宏欣, 周穗华, 冯士民. 基于弱形式解的粒子流滤波器[J]. 控制与决策, 2015, 30(5)：853-858.

Zhang Hongxin, Zhou Suihua, Feng Shimin. Weak solution based particle flow filter[J]. Control and Decision, 2015, 30(5)：853-858.

[14] Zienkiewicz O C, Taylor R L. The finite element method for solid and structural mechanics[M]. Cambridge: Elsevier Butterworth-Heinemann, 2005: 17-44.

[15] 刘凯.粒子滤波在单通道信号分离中的应用研究[D].合肥: 中国科学技术大学, 2007:65-92.

Liu Kai.Study on particle filtering and its application in single-channel blind separation[D]. Hefei: University of Science and Technology of China, 2007:65-92.