基于典型地物字典学习的遥感图像分块重构方法
王 轩 孙权森 刘佶鑫
(1. 南京理工大学计算机科学与工程学院,南京, 210094;2. 南京邮电大学宽带无线通信技术教育部工程研究中心,南京, 210003)
引 言
遥感图像数据发展具有高分辨率、高光谱和多时相的趋势,导致信息量的与日俱增,大大增加了存储和传输的代价。因而与普通成像相比,遥感成像对数据压缩技术提出了更高的要求。为此,压缩感知作为一种新理论被引入相关领域。压缩感知理论[1]指出,只要信号是稀疏的或者在某一变换空间是稀疏的、可压缩的,就可以以远低于奈奎斯特频率进行采样,并能够精确地重构原始信号。因此,对遥感图像采用压缩感知理论进行图像压缩与重构具有节约工作时间、节省存储和传输代价的优势,仅需少量数据即可重构原始的高分辨率遥感图像。
根据Donoho和Candes等的理论[2],信号在字典下的表示系数越稀疏,则重构质量越高。因此,设计简单、高效、通用性强和重构图像质量高的字典学习算法十分重要,是目前主要研究方向之一。近年来稀疏编码在信号和图像处理领域应用广泛。文献[3]给出了关于求稀疏解的方法,该方法试图从一个典型的较大的过完备字典中找到一小部分最能表示一个特定信号的向量[4,5]。这些算法假设存在一个合适的字典矩阵具有一定的性质,以保证信号表示的稀疏性。确切地说,选择一个字典矩阵对于解的稀疏性和信号表示的准确性有重要影响。
字典学习可提取样本数据的内部结构特征,已被广泛应用于去噪[6]、特征提取[7]、模式识别与分类[8]以及压缩感知等领域。Elad等采取了K-SVD(K-singular value decomposition)[9]的字典学习算法,采用超完备的冗余函数系统代替传统的正交基函数,为信号自适应地稀疏扩展提供了极大的灵活性。在重构过程中采取正交匹配追踪(Orthogonal matching pursuit,OMP)的方法[5],信号稀疏表示的重构质量上略有提升。在文献[9]中,作者把K-SVD与包括MOD[10]在内的其他字典学习算法在图像压缩和重建方面大量作对比。人脸识别是这种字典学习方法的另一应用[11]。文献[12-14]针对视频压缩、视频编码和声呐图像数据提出了字典学习和相应的快速重构方法。
本文针对不同地物的高分辨率遥感图像,提出一种基于稀疏表示和典型地物字典学习的遥感图像分块压缩重构算法,使用K-SVD字典学习算法训练典型地物的字典。重构过程首先对部分观测数据迭代求解出稀疏表示原图像的原子,然后优先使用相邻块的部分原子求表示残差,以减少迭代次数。该算法与其他字典如离散余弦变换(Discrete Cosine transform,DCT)、离散小波变换(Discrete wavelet transform, DWT)等压缩重构算法相比,保留了图像的结构信息,高效地重构出遥感图像。
1 压缩感知及其在遥感图像重构中的应用
1.1 压缩感知基本模型
压缩感知理论要求,压缩信号f必须在某个变换域是稀疏的,自然信号可以通过某种变换进行稀疏表示,即f=Dx,x为信号f在某种变换的稀疏表示,并有
y=Φf=ΦDx=Ψx
(1)
式中:Φ为观测矩阵;y是稀疏信号x关于观测矩阵的测量值。如果Φ满足约束等距条件可以通过求解
(2)
的最优范数问题来重构稀疏信号x。接着通过下式恢复原始信号
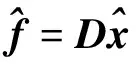
(3)
通过对遥感图像进行有效的随机观测,可将信息汇聚到少量的采样数据中;同时,优良的字典设计和重构方法的选择和能够保证由少量的采样数据恢复出原始的高分辨率遥感图像。
1.2 K-SVD字典学习
目前,字典构造方法一般分为两种:解析方法和学习方法[15]。基于解析方法构造的字典通过事先定义好的某种数学变换或调和分析方法来构造, 字典中的每个原子可用数学函数或少量的参数来刻画, 如离散余弦变换、小波变换等。该方法虽然构造相对简单, 计算复杂度低, 但原子的基本形状固定, 原子的形态不够丰富, 不能与图像本身的复杂结构最佳匹配。
近年来人们开始根据数据或信号本身来学习过完备字典, 这类字典中的原子与训练集中的信号本身相适应。与基于解析方法的字典相比, 通过学习获得的字典原子数量更多, 形态更丰富, 能更好地与信号或图像本身的结构匹配, 具有更稀疏的表示。
字典学习可提取样本数据的内部结构特征。其学习方法一般可以通过优化下式获取,即
(4)
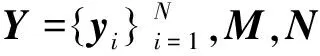
通过对某一类的图像进行训练以获得字典的方法,最典型的方法是K-SVD算法。K-SVD算法用来学习一个专用字典矩阵,最好地适应一组训练集。K-SVD在现有的稀疏编码追踪方法中适应性较强,可以用于表示数据。
该方法针对目标函数式(4),首先进行稀疏表示,即对固定字典D,计算的表示系数αi,有
(5)

(6)

(7)

1.3 重构算法
压缩感知信号重构指的是由M次测量向量x重构长度为N的稀疏信号y的过程[16]。可以通过求解最小范数问题加以解决,但最小范数是一个NP-hard问题,需要穷举x中非零值所有的种排列可能。OMP[5]是一种贪婪迭代算法,其基本思想是在每一次的迭代过程中,从过完备原子库里选择与信号最匹配的原子来构建稀疏逼近,并求出信号表示残差,然后继续选择与信号残差最为匹配的原子,通过递归地对已选择原子集合进行正交化以保证迭代的最优性,经过一定次数的迭代,信号可以由一些原子线性表示。正交匹配追踪算法以极大概率准确重构信号,而且比最小范数法更快,在图像重构中应用广泛。
2 基于字典学习与邻域优化的遥感图像分块重构
遥感图像是传感器所获得信息的产物,是遥感探测目标的信息载体。针对不同类型地物的遥感图像选择最优的稀疏表示方法,可以有效地提高遥感图像重构质量,便于后期的信息提取工作。图1是本文方法的流程图,其中实线框内部分为本方法主要内容。

图1 字典训练与图像分块重构流程图Fig.1 Picture of dictionary training and image block reconstruction
2.1 不同地物遥感图像的特性分析
地球表面不同类型的地物在遥感影像上具有不同的影像特征,因而能够在遥感影像上区分和识别不同的地物类型。其中,水域、农田、山脉和城市等是陆地表面典型的地物类型,既有自然地物,也有人工改造形成的地物。水域对太阳光吸收、反射和透射随波长的变化而变化,总体上吸收大于反射和透射,灰度直方图见图2(a)。同时,由于水体表面总体上是平的,不同入射角的光线有不同的反射能力,遥感图像上水体也会有不同的影像特征。农田及植被在地表分布较广,是地球生态系统的重要组成部分。农田具有典型的波谱选择性反射特性,在可见光反射率都比较低,灰度直方图见图2(b)。在遥感影像上,农田的影像特征主要体现在色调、形状和图案等方面。农田影像有人为造成的块状、条带状等几何形态。不同质地的山脉,其波谱特性不同。遥感图像色调的深浅与山脉土壤有机质含量、湿度大小和质地粗细有关。有机质含量高、湿度大且质地细的色调较深。图2(c)为一幅山脉图像的灰度直方图。城市既是人类最为集中的地域,又是一定地域的政治、经济和文化活动的中心。城市的影像特征表现在灰度、形状及空间布局等方面,灰度直方图见图2(d)。城市构成以房屋为主,兼有道路、植被和水体等,具有这些地物的全部波谱、形态、布局和图形结构等特征。房屋不同质地的屋顶具有不同的波谱特征。石棉屋顶和塑料屋顶的反射率较高。
2.2 基于典型地物的字典学习
信号的最佳稀疏表示是压缩感知理论应用的基础和前提,只有选择合适的字典表示信号才能保证信号的稀疏度,从而保证信号的重构精度。而遥感图像内容丰富、数据类型多且目标小,且包含了丰富的纹理信息,不同地物通常呈现独特的多尺度特征。
针对2.1节中提到的水域、农田、山脉和城市4种陆地上典型的地物类型,对训练集中的遥感图像进行分类,构建4组训练集,参考图像如图3所示。在每组训练集上使用K-SVD的字典学习方法,训练得到分类联合字典,其中ω为字典类别数。


图3 4类典型地物遥感图像

图4 分块处理示意图 Fig.4 Block processing schematic
2.3 基于邻域优化的分块重构方法
由于对同一遥感图像的局部区域的进行稀疏表示时,使用的过完备字典中的部分原子存在重复或相似。考虑将图像分块,首先对分块图像的部分块的观测值(图4中灰色块),从过完备字典中使用OMP贪婪迭代算法迭代求解出一组能稀疏表示的原子;对于其邻域内的观测值(图4中白色块),先用这些原子中的一部分求稀疏表示残差,再对残差进行迭代求解得到剩余的稀疏表示原子。本文采用的是每3×3的9个块中,先对中心的1块求解,再根据其求解使用的原子优先对其周围邻域的8个块求表示残差,进一步求解,大大提升了邻域块的重构效率。如果扩大邻域范围,例如对5×5的25个块为一组进行处理,效率将更高,但对重构质量有一定损失。
具体步骤如下:
(1) 遥感图像压缩感知观测过程。
对原图像f及观测矩阵Φ进行分块观测,得到观测值y(i,j为图像块的行、列号),即
yi,j=Φi,jfi,ji,j=1,2,…
(8)
(2) 遥感图像块重构过程。
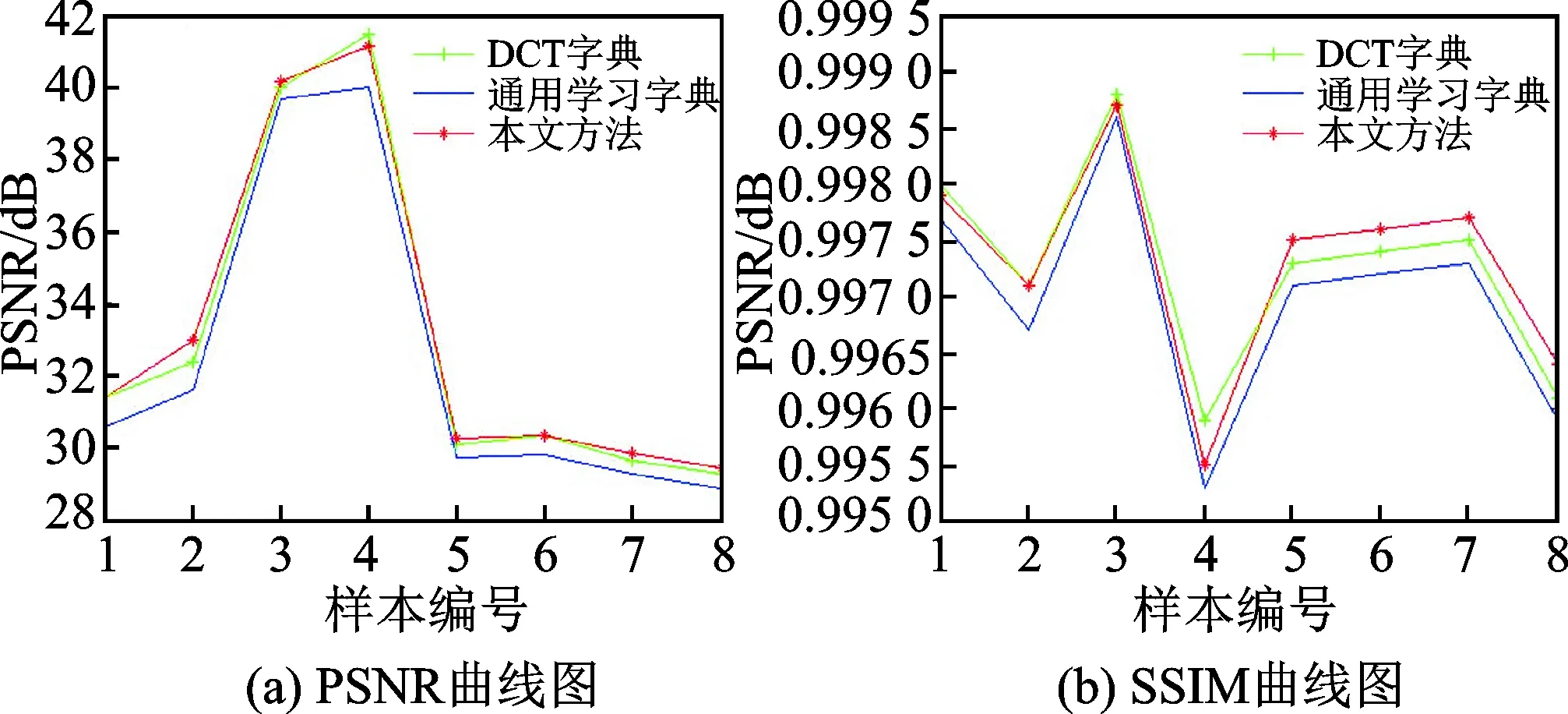
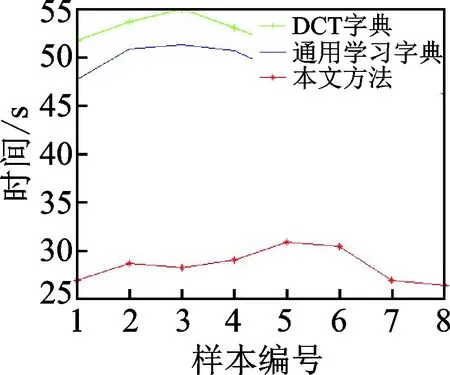
输入:观测矩阵Φ,典型地物的学习字典,稀疏度k,观测值y,信号表示残差最小值,图像总块数N,保留原子个数s(s 输出:可以稀疏表示原图像的原子索引集Λ。 步骤1:初始化残差r=yi,j,索引集Λ0=Ø 步骤2:对行列号为y(i=3n+2,j=3n+2)的观测值块(图5中灰色块),找出残差r和字典Dβ积中最大值所对应的脚标λ (9) 更新索引集 Λt=Λt-1∪{λt} (10) 记录下字典中找到的稀疏表示原图像的原子集合 Φt=[Φt-1,dj] (11) 由最小二乘得到 (12) 更新残差 (13) t=t+1,判断是否满足t≥k或r 步骤3: 处理步骤2中的观测值块(图4中白色块):y(i=3n+2,j=3n+2)的8个邻域块:y(i=3n+1,j=3n+1),y(i=3n+2,j=3n+1),y(i=3n+3,j=3n+1),y(i=3n+1,j=3n+2),y(i=3n+3,j=3n+2),y(i=3n+1,j=3n+3),(i=3n+2,j=3n+3),y(i=3n+3,j=3n+3),初始化稀疏表示原子集合Φ0和索引集Λ0,保留y(i=3n+2,j=3n+2)的s个原子及其索引 Φ0=Φs (14) Λ0=Λs (15) 计算残差 (16) (17) 继续查找原子,同步骤2。 若n 步骤4:由步骤2和步骤3中找到的索引集恢复原图像块,即 (18) 为了验证本文方法针对典型地物的遥感图像的重构效果以及时间效率,分别用3种方法进行对比:使用固定的DCT字典与OMP重构方法;未分类的遥感图像训练的通用学习字典与OMP重构方法;以及本文提出的4种典型地物的学习字典与邻域分块优化重构方法。对4类典型地物的遥感图像构建样本集,包括水域、农田、山脉和城市等4种陆地典型地物,并从中选出部分图像进行测试。 首先从每类典型地物图像中选取100幅像素为512×512的图像作为训练集,分别进行K-SVD字典学习,迭代次数30次,学习字典参数为:块大小8×8,原子个数256,稀疏度10,得到4种典型地物的学习字典。用3种方法的字典对压缩后的4类典型地物各10组测试数据数据进行重构,测试图像大小1 024×1 024像素,相邻块取8个,重构时保留的原子个数取9个。为了直观地比较试验结果,本文从测试集中选取了一幅山脉图像展示了试验效果。图5(a)为输入的测试图像,图5(b)为本方法重构后的图像。可以看出直观效果差别不大。 本文采用了峰值信噪比(Peak signal to noise ratio,PSNR)和结构相似度索引(Structural similarity index measurement,SSIM)为遥感图像重构结果的图像质量评价指标。PSNR 值越大,SSIM 值越大,则重构图像与参考图像就越接近,说明算法效果越好。用部分测试图像运行结果绘制了两项指标的曲线图如图6所示。 图5 测试图像与重构图像 图6 DCT字典、通用学习字典及本文方法重构效果曲线图 图7 DCT字典、通用学习字典及本文方法重构时间曲线图 Fig.7 Reconstruction time graph of DCT diction-ary, general dictionary and proposed method 可以看出本文方法采用典型地物的字典(红色“*-”线)在重构质量上,PSNR与SSIM两项指标较通用学习字典(蓝色“—”线)有明显提升。除样本3,4(水域图像)的重构结果略低于DCT字典,其余样本(农田、山脉、城市图像)与DCT字典(绿色“+-”线)相比略有提高。且PSNR均稳定在28 dB以上。 图7是3种方法的重构时间,可以看出无论是DCT字典或通用学习字典,重构时间在45 s以上。而本文方法(图中红色“*-”线)大大缩短了重构时间,均在35 s以内,平均占DCT字典重构时间的54.5%,效率较高。因此,本文的基于典型地物字典学习及邻域分块优化的重构方法较DCT字典和训练的K-SVD学习字典在重构质量上稍有提升,在重构时间上优势较明显。 基于遥感图像的压缩感知模型,本文针对现有的字典构造方法及重构方法中存在不同地物图像重构效果差别大,重构时间有待提升等问题,提出了一种新的字典学习及分块重构方法。该方法在联合字典学习的基础上引入了分类字典的概念。依据4类典型地物的遥感图像训练冗余字典。在重构过程中,对邻域图像块保留部分字典原子以提升重构效率。实验表明,本方法在保证重构效果的同时,在重构时间上有大幅提升。此外,本方法还可以通过调整相邻块数和保留原子个数来调整重构时间或重构图像质量,在通过观测值选择相应字典方面是下一步研究的重点。 参考文献: [1] Candes E J, Romberg J. Quantitative robust uncertainty principles and optimally sparse decompositions[J]. Foundations of Computational Mathematics, 2006, 6(2):227-254. [2] Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4):1289-1306. [3] Bruckstein A M, Elad M. From sparse solutions of systems of equations to sparse modeling of signals and images[J]. SIAM Review, 2009, 51(1): 34-81. [4] Chen S S, Donoho D L, Saunders M A. Atomic decomposition by basis pursuit[J]. SIAM Review, 2001, 43(1):33-61. [5] Tropp J A, Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2008, 53(12):4655-4666. [6] Elad M, Aharon M. Image denoising via sparse and redundant representations over learned dictionaries[J]. IEEE Transactions on Image Processing, 2007, 15(12):3736-3745. [7] Ramirez I, Sprechmann P, Sapiro G. Classification and clustering via dictionary learning with structured incoherence and shared features[C]∥IEEE Conference on Computer Vision & Pattern Recognition (CVPR).[S.l.]:IEEE, 2010:3501-3508. [8] Jiang Z, Lin Z, Davis L S. Learning a discriminative dictionary for sparse coding via label consistent K-SVD[C]∥IEEE Conference on Computer Vision & Pattern Recognition (CVPR).[S.l.]:IEEE, 2011:1697-1704. [9] Aharon M, Elad M, Bruckstein A K. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311-4322. [10] Kreutz-Delgado K, Murray J F, Rao B D, et al. Dictionary learning algorithms for sparse representation[J]. Neural Computation, 2006, 15(2):349-396. [11] Zhang Q, Li B. Discriminative K-SVD for dictionary learning in face recognition[C]∥IEEE Conference on Computer Vision & Pattern Recognition (CVPR).[S.l.]:IEEE, 2010:2691-2698. [12] Chen H W, Kang L W, Lu C S. Dictionary learning-based distributed compressive video sensing[C]∥Picture Coding Symposium (PCS). Nagoya, Japan: [s.n.],2010:210-213. [13] Azimi-Sadjadi M R, Kopacz J, Klausner N. K-SVD dictionary learning using a fast OMP with applications[C]∥IEEE International Conference on Image Processing (ICIP).[S.l.]:IEEE, 2014:1599-1603. [14] 郭继昌, 金卯亨嘉. 一种基于字典学习的压缩感知视频编解码模型[J]. 数据采集与处理, 2015, 30(1):59-67. Guo Jicang, Jin Maohengjia. Dictionary learning-based compressive video sensing codec model[J]. Journal of Data Acquisition and Processing, 2015,30(1):59-67. [15] 练秋生, 石保顺, 陈书贞. 字典学习模型、算法及其应用研究进展[J]. 自动化学报, 2015, 41(2):240-260. Lian Qiusheng, Shi Baoshun, Chen Shuzhen. Research advances on dictionary learning models, algorithms and applications[J]. Acta Automatica Sinica, 2015, 41(2):240-260. [16] 李树涛, 魏丹. 压缩传感综述[J]. 自动化学报, 2009, 35(11):1369-1377. Li Shutao , Wei Dan. A survey on compressive sensing[J]. Acta Automatica Sinica, 2009, 35(11):1369-1377.
3 实验验证

4 结束语

