A sludge volume index(SVI)model based on the multivariate local quadratic polynomial regression method

Honggui Han *,Xiaolong Wu Luming Ge Junfei Qiao

1 College of Automation,Faculty of Information Technology,Beijing University of Technology,Beijing 100124,China

2 Beijing Key Laboratory of Computational Intelligence and Intelligent System,Beijing 100124,China

1.Introduction

Activated sludge process(ASP)is the most commonly used technology in the wastewater treatment process(WWTP)[1-3].In ASP,the activated sludge unitconsists of the bioreactors and the secondary settling tanks[4].Sludge bulking,a term used to describe the excessive growth of filamentous bacteria,is a common operational problem in ASP[5].Sludge bulking will affect the sludge settle ability in the secondary clarifiers as well as effluent quality in WWTP[6].The operational and seasonal variations in ASP(such as dissolved oxygen concentration(DO),pH,substrate limiting conditions)will influence the structure of the flocs to cause sludge bulking.Therefore,how to find the reasons of sludge bulking is still an open problem[7].

To find a general explanation of sludge bulking,several theories have been reported,such as the diffusion-based selection[3],the kinetic selection theory[8],the storage selection theory[9]and the nitric oxide(NO)hypothesis[10].However,most of them still lack experimental verification[11].In recent years,many researchers focused on the enumeration of the bacterial community by using molecular approaches to identify filamentous bacteria for explaining sludge bulking(including denaturing gradient gel electrophoresis[12],16S rRNA gene clone library analysis[13]and transmission electron microscopy[14]).For these molecular approaches,since there are many microorganisms related to the sludge bulking,and many new types of filamentous bacteria have been identified.It is more and more complex to determine sludge bulking by identifying filamentous bacteria[15].In addition,the microscopic identification of filamentous bacteria requires a well-trained operator to avoid the wrong judgments[16].

Recently,in order to quantify sludge bulking,the SVI is used to measure the settle ability of activated sludge[17].SVI is the most common parameter to determine the settling characteristics of suspended growth activated sludge solids[18].As a general guideline,bulking is said to occur when the SVI is higher than 150 ml·g-1,regardless of its cause[19].To obtain the information about sludge bulking,the value of SVI should be monitored.Giokaset al.developed a nonlinear model using an integrated and unified settling characteristics database for detecting SVI values[20].This nonlinear model can be applied for designing the secondary settling tank for WWTPs.Raminet al.developed a new settling velocity model,including hindered,transient and compression settling,to test and diagnosis sludge settling[21].The experimental results show that the representation of compression settling in the proposed model can significantly influence the prediction of sludge distribution in the secondary settling tanks.However,due to the complex biological reactions,as well as highly time-varying and multivariable,these methods are still difficult to be used in a real WWTP[22].

To overcome the above problems,in recent years,the data-driven methods have been developed as an efficient alternative way for predicting sludge bulking,in which the necessary process information can be extracted directly from the process data.For example,Smetset al.introduced a dynamic auto-regressive exogenous(ARX)model to predict the SVI values in[23].This proposed dynamic ARX model is investigated as a function of organic loading and digital image analysis information.The experiment results show that this proposed dynamic ARX model can predict the SVI values online.Xavieret al.proposed a risk assessment model based on a knowledge-based decision tree to detect the favorable conditions for sludge bulking in[3].The simulation results demonstrate that this risk assessment model is able to detect the conditions of sludge bulking in the secondary clarifier.In addition,Bagheriet al.developed a hybrid artificial neural networks-genetic algorithm method for predicting SVI values in[24].The comparison of the results indicated that the multi-layer perceptron artificial neural networks-genetic algorithm model is more accurate because of higher coefficient of determination and lower root mean squared error values.Moreover,a self-organizing radial basis function(SORBF)neural network was introduced to predict the SVI values online in[25].In this method,a growing and pruning algorithm is designed to improve the generalization performance of the model and the predicting accuracy of SVI values,and some other models,based on the artificial neural networks,have been widely reported for process monitoring in WWTPs[26].Although many studies have been carried out,the available sludge bulking predicting technologies are still not as developed as other process industries[27].Thus,a cause-effect relationship between the specific microorganisms and their roles in filamentous bulking are likely to be studied[28].

To obtain a model with satisfactory accuracy and interpretation capability of the sludge bulking,a multivariate local quadratic polynomial regression(MLQPR)method,based on the historical measurements of easy-to-measure process variables,is develop to predict the SVI values in this paper.In addition,a local estimation method is developed to improve the predicting accuracy.In order to show the effectiveness of the proposed method,it is applied to predict the SVI values in a real WWTP.The remainder of this paper is as follows.The definition of SVI and the hardware setup are firstly discussed.Then,the MLQPR method,as well as the data preprocessing and variable selection,are developed to design a model for predicting the SVI values.Furthermore,this proposed model is applied in a real WWTP.The experimental results demonstrate the effectiveness of the proposed method.The final section gives the conclusions.

2.SVI Prediction

2.1.SVI

Sludge settling is one of the most important characteristics of ASP,which is the most commonly applied technology for WWTP.Sludge bulking,leading to poor settling in the secondary clarifier and allowing the unsettled biomass to escape with the effluent,is caused by the overdevelopment of filamentous bacteria.Sludge bulking is one of the main operational problems in activated sludge systems.

The SVI values are the standard measure of the physical characteristics of activated sludge solids which were used to quantitatively characterize sludge bulking.When the SVI of a given mixed liquor sample is low,the settle able sludge fraction is dense with good settle ability[29].SVI indicates the tendency of activated sludge solids to thicken or to become concentrated during the sedimentation process.SVI is calculated in the following manners:1)The mixed liquor sample from the aeration basin is settled for 30 min.2)The suspended solids concentration of the same mixed liquor is determined.3)The SVI values are calculated by dividing the measured wet volume of the settled sludge.

2.2.Hardware setup

In order to introduce the proposed method,a sampling system is installed.The anaerobic-anoxic-oxic(A2/O)wastewater treatment system is shown in Fig.1.This A2/O wastewater treatment system includes an anaerobic tank,an anoxic tank and three oxic tanks.These tanks are constantly mixed through using the mechanical mixers.The average working volume of each tank is 60 L(a height of 110 cm and an internal diameter of 15 cm).The aeration tank is followed by a sedimentation tank(30 L).After the pretreatment processes,the wastewater enters to the anaerobic tank with a hydraulic retention time(HRT)of 0.5 h and then to the anoxic tank.The anoxic phase is completed with a HRT of 2 h and then wastewater to the aeration tank.The F/M ratio changes from 0.1 to 0.9 in the aeration tank.The aeration is performed in the aeration tank with a HRT of 8 h,and then the wastewater enters the secondary clarifier.The internal recycle is performed from the last aerobic tank to the last anoxic tank.A gas stripping device is installed at the bottom of secondary clarifier.Then the sludge in the secondary clarifier is regularly pumped into the sludge tank to ensure the stable sludge digestion.The external recycle is operated from the under flow of the secondary settler to the front end of the plant.The effluent is disinfected at the end of the process and the treated wastewater is discharged into the river.Moreover,the sludge used in this simple A2/O wastewater treatment system is from a real WWTP.

Fig.1.Schematic diagram of A2/O wastewater treatment system.

In addition,the online sensors are schematically distributed in the experimental hardware setup.The online sensors consist of twelve parts:the influent flow rate(Qin)mater,the external circulating flow rate(Qet)mater,the effluent flow rate(Qw)mater,the biological oxygen demand(BOD)instrument,the chemical oxygen demand(COD)instrument,the DO concentration probe,the pH instrument,the temperature(TEM)meter,three MLSS instrument and the ammonia nitrogen(NH4-N)instrument.Since there is no direct contact between the sensors and the PC-computer,a data transmitting system has been designed.All the instruments are operated in continuous/online measurement mode in the present study.The sampling points and positions are clearly shown in Fig.1.The monitored parameters includesQin,Qet,Qw,DO,food-to-microorganism ratio(F/M),sludge re flux ratio(Rr),sludge retention time(SRT),TEM,influent BOD,influent COD,NH4-N,effluent pH value(pH),MLSS1(sludge concentration at sampling point 3),MLSS2(sludge concentration at sampling point 5)and MLSS3(sludge concentration at sampling point 6).These main apparatus and instruments used in this setup are explained in Table 1.

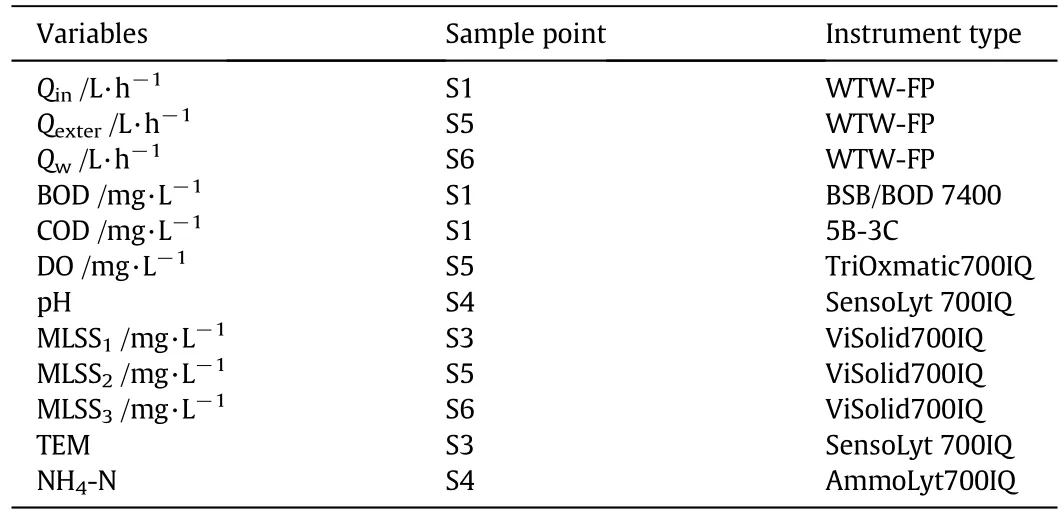
Table 1 The information of the online measured variables

The values of DO,NH4-N,BOD,COD,TEM,pH,Qin,Qet,Qw,MLSS1,MLSS2and MLSS3are obtained by the online instruments.Since it is time consuming and less efficient to import the data through the USB ports,a data recorder is installed to automatically record the data from the online instruments and import the data into the computer directly.The values of F/M,Rr and SRT are gained from the calculation of some of the above parameters automatically.F/M is calculated using the BOD,Qinand MLSS1.Rr is computed using theQinandQet.SRT is related with MLSS1,MLSS2,MLSS3andQw.Furthermore,the calculation is performed using the mean value of a full day sampled MLSS1,MLSS2and MLSS3,which can represent the changes in sludge concentration,so as to ensure the accuracy of the calculation.

2.3.Variable selection

The normalized data matrix of the monitored parameters is M,anm×kmatrix.M can be factored into three matrices by the principal component analysis(PCA)method:

where S=[s1,…,sk],anm×kmatrix,is the principal component scores of M;E is the residual matrix,pi;andk×1 matrix,is the eigenvector corresponding to λi(e.g.theith largest eigenvalue)of MTM,P=[p1,…,pk].kis the number of characteristic variablesis the contribution rate ofith principal component,is the interpreted cumulative contribution rate of the firstjprincipal components.The maximum of pi(i=1,…,j)indicates the highest existing correlation among variables and corresponding components.If the number in thelth(l＜k)row of piis the maximum of pi,thelth characteristic variable is chosen as a principal variable.Based on the results of PCA,DO,F/M,Rr,SRT and TEM,the principal variables are chosen.

2.4.Multivariate local quadratic polynomial regression(MLQPR)method

In this study,the MLQPR method is used to design the SVI model according to date of the input-output variables.This method combines the multivariate quadratic polynomial regression(MQPR)model and the local linear regression(LLR).The MQPR equation is defined as:

wheret=1,2,…,m,α(t)=[α0(t),α1(t),α2(t),…,αp(t)]Tis the regression coefficient matrix,X(t)=[X1(t),X2(t)],X1(t)=[x0(t),x1(t),…,xn(t)],X2(t)=[x1(t)x2(t),x1(t)x3(t),…,xn(t)xn(t)],x0(t)=1,xi(t)is theith variable of x(t),x(t)=[DO(t),F/M(t),Rr(t),SRT(t),TEM(t)].

In fact,the multivariate quadratic polynomial relationship of the MQPR model cannot indicate the impact of each variable.Therefore,a significant test should be taken for each variable to determine its state.The test statistic is defined as[30].

wheree(t)=yd(t)-y1(t),yd(t)is real output value of thetth observation sample,ciirepresents theith element of main diagonal of the matrix(XT(t)X(t))-1.

The significance of regression coefficients is analyzed according to the test indicators in statistics.Given the significance level λ=0.05,the critical value is obtained asTλ/2(m-p-1),if|η(t)|＞Tλ/2(m-p-1),theith regression coefficient of α(t)is not significant and theith variable of X(t)is deleted.After eliminating the nonsignificant input variables in X(t),the MLQPR model can be written as:

where Z(t)=[z0(t),z1(t),…,zq(t)],zi(t),(i=0,1,…,q)represents the remaining input variables in X(t),andz0(t)=1,θ(t)=[θ0(t),θ1(t),…,θq(t)]Tis the coefficient matrix,and

wheretis in the neighborhood oft0,θ′iis the derivative of θi(t).The square sum of errors is:

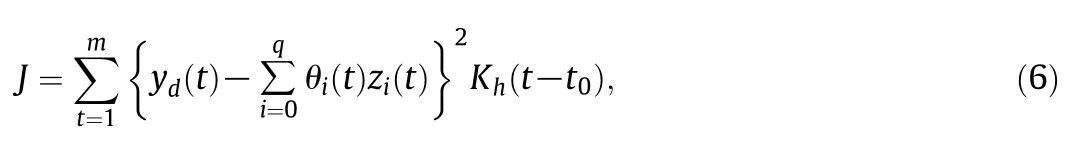
whereKh(t-t0)=his the bandwidth used to control of the size of the local neighborhood.

To minimize the square sum of errors in Eq.(6),the coefficients are calculated based on the weighted least squares:and three indicators are considered to determine the appropriate value of bandwidthh0.

where^y（t）|his the estimated value at thetth sample when the smoothing parameter ish.The value ofC(h)is given within a small range.h′=h+1,U(h′)is the relative variation ofC(h′),andU(h′) ≤1,D(h′)is the relative variation ofU(h′).C(h)andD(h)are limited to a reasonable range respectively.The lower bound ofD(h)is given.

2.5.SVI model based on MLQPR

To express the relation between the selected monitored process variables and the SVI clearly,the MLQPR model of SVI is discussed in details.In fact,the error of MLQPR model is related to the indicators ofC(h),U(h)andD(h).The MLQPR model is able to obtain suitable test performance whenC(h)is small.However,whenC(h)is close to zero,the generalization performance of the model is poor due to the noise in the data.Therefore,C(h)is limited within the range of[0.0003 0.0015]in this paper.Meanwhile,U(h)is used to judge the local variation performance of the MLQPR model.WhenU(h)is close to 1,the MLQPR model will be easily subjected to noise.On the other hand,ifU(h)is close to 0,the complexity of the MLQPR model will be reduced and the performance of the MLQPR model will be poor.Here,theU(h)is given within the range of[0.01 0.03].Moreover,the minimum ofD(h)is used to judge the stability of the MLQPR model.Based on the former results,the minimum ofD(h)is pre-set as 0.001.Then,according to Eqs.(2)-(4),the MSQPR model is obtained,and the appropriatehis selected by Eqs.(11)-(13).Finally,based on the above discussion,the MLQPR model is:

where θ0(t),θ1(t),…,θ11(t)represent the corresponding coefficients of each variable in the multivariate local quadratic polynomial regression model.

The basic idea of the proposed MLQPR model is to improve the precision of the final multivariate quadratic polynomial regression by taking the local approximation scheme.Initially,an MQPR model is established and the significance of each regression coefficient is tested.In addition,a local approximation scheme is applied into the regression coefficient.For clarification,the procedure of the establishment of the MLQPR model can be summarized as follows.

Step 1)Create an MQPR model as Eq.(2).The input variables not only contain the selected process variable,but also the quadratic combination of them.

Step 2)The hypothesis test in Eq.(3)is used to analyze the significance of regression coefficients.The least significant coefficient and its corresponding input variable is deleted,and the remaining input variables are used to establish a new quadratic polynomial regression model.

Step 3)Repeat Step 2,until all the regression coefficients are significant.

Step 4)The remaining input variables are used as the input variables of MLQPR model in Eq.(4).The θi(t)is calculated using Eq.(8).The initialhis given.

Step 5)The value ofC(h)andU(h)are given within a small range,the lower bound ofD(h)is given.Compute theC(h)using Eq.(11).

Step 6)h=h+1,Compute theU(h)andD(h)using Eqs.(12)and(13).IfC(h)orU(h)exceeds the limit of the given small range,orD(h)is less than the lower bound ofD(h),stop.Then go to step 4,the MLQPR model is obtained.

3.Experiment Studies

In this experiment,the MLQPR model is proposed to predict the SVI values.The DO,F/M,Rr,SRT and TEM are used as the inputs for the model to estimate the SVI values.A dataset containing 600 process samples(from1st March 2015 to 30th September 2015)was selected in this experiment.After deleting abnormal data,583 samples were obtained and normalized.The last 100 samples were used as testing data,while the remaining samples were employed as training data.All data are normalized and de-normalized between 0 and 1 before and after application in the MLQPR model.

All the simulations are programmed with MATLAB version 7.01,and were run on a Pentium 4 with a clock speed of2.6 GHZ and 1 GB of RAM,under a Microsoft Windows 8 environment.

In order to evaluate the performance of the proposed method,the following indices are used.The root mean square error(RMSE)is defined as:

the Theil inequality coefficient(TIC)is defined as:

the prediction accuracy is defined as:

wheremis the number of samples of the test set;yd(t)is real output of thetth observation sample;^y（t）is the predictive value of thetth observation sample.

3.1.SVI prediction and evaluation of the MLQPR method

For indicating the effectiveness of the different models,in this study,two cases of the evaluations are discussed.In case 1 study,the MLQPR comparison to the same MLQPR method when the training dataset is prone to the disturbance.In case 2 study,the MLQPR comparison to the other local regression models and the SVI mathematical models.

3.1.1.Case 1 study

The predicting results of the MLQPR model with and without disturbance are shown in details.In this case,the disturbance was normally distributed with a standard deviation of 0.0316.

The optimum bandwidth of kernel function ish=31.The predicting results of SVI are shown in Figs.2-3.Fig.2 displays the predicting results of the SVI values without disturbance,together with the real process output.The predicting results of the SVI values in the condition that the training dataset is prone to the disturbance are presented in Fig.3,together with the real process output.Fig.4 shows the error between the plant output and the testing results.When there exists disturbance in the input-output dataset,the error between the plant output and the testing results is given in Fig.5.More specifically,the blank parts of Figs.2 and 3 are the real SVI values.The blue parts in Figs.2 and 4 represent the predicted SVI values and the errors between the plant output and the testing results when there is no disturbance.The red parts in Figs.3 and 5 are the predicted SVI values and the errors between the plant output and the testing results with disturbance.The predicting errors in both conditions,respectively shown in Figs.4 and 5,are less than ±2.5 ml·g-1.Moreover,the performance of the two conditions is compared in Table 2.The root mean square error,the Theil inequality coefficient,and the prediction accuracy are computed according to Eq.(17),Eq.(18)and Eq.(19).

Fig.2.The predicting outputs without disturbance.

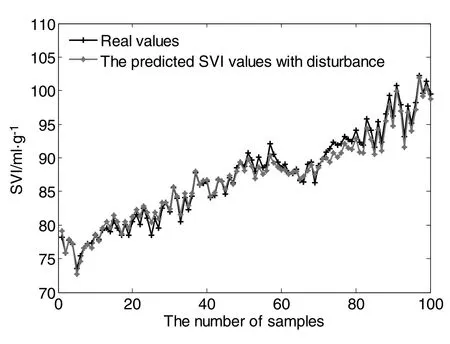
Fig.3.The predicting outputs with disturbance.

Fig.4.The predicting errors without disturbance.

Fig.5.The predicting errors with disturbance.

Based on the results in Table 2,the following specific comments canbe made.1)The accuracies of the proposed MLQPR models are better for SVI prediction,due to the low RMSE,low TIC and high accuracy whether there exists disturbance or not.2)The comparisons demonstrate that the proposed model has a certain ability of interference immunity.

Table 2 Comparative performance for SVI prediction

3.1.2.Case 2 study

In this case,the MLQPR model is compared with the other models:the LLR model,the MLQPR1 model(without squared terms in the model).The variables and descriptions of them are shown in Table 3.

The performance comparison of these three methods is shown inTable 4,and the root mean square error,Theil inequality coefficient,prediction accuracy are computed according to Eq.(17),Eq.(18)and Eq.(19).

Table 3 The variables and descriptions for the local regression methods

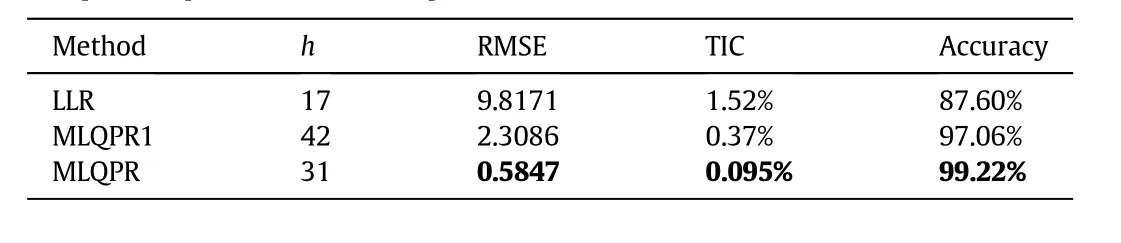
Table 4 Comparative performance for SVI prediction

From Table 4,the following specific comments can be made.1)The accuracy of the proposed MLQPR model is better than that of the LLR method and the MLQPR1 model.2)The testing RMSE value of the proposed MLQPR model is the smallest.The comparisons demonstrate that the MLQPR model is more suitable for the SVI prediction than some existing methods.

In addition,the predicting performance of MLQPR model is compared to the image analysis model in[18],the mathematic model in[20],the dynamic ARX model in[22],the feed forward neural network in[29],and the SORBF in[26].Their performance is compared in Table 5,for fair comparison,some experimental result of the other SVI models are the same as the initial papers.The results in Table 5 indicate that the prediction system with MLQPR method has the following advantages for SVI prediction compared to other methods.(1)As shown in the Table 5,the proposed MLQPR prediction method obtains the best testing RMSE values for the predictions of SVI than other prediction methods.(2)In this case,the MLQPR model gets the best accuracy(best value is 99.7%)both for the minima and maxima values.The results show that the SVI values can be predicted well by the MLQPR method to meet the limits specified by the regulations.(3)This dynamic characteristic of MLQPR is very useful to predict the SVI values for the WWTP.

Table 5 A comparison of the performance of different models

3.2.Analysis of the experimental results

The MLQPR method has been successfully used in the process industries.It has been proved to be an efficient method to predict SVI values according to the above results.To gain deeper understanding of the proposed SVI predicting plant with the MLQPR method,the special comparisons of the SVI prediction performance among the two methods:the LLR and the MLQPR1 were analyzed.According to the results in Table 3,it can be seen that the proposed MLQPR not only can obtain a compact structure,but also can obtain a high-precision prediction result than other methods.Compared with the adaptive methods(LLR and MLQPR1),it is more suitable for modeling the nonlinear system by utilizing the significance test for the regression coefficients.

For comparison purposes,the image analysis,the mathematic model,the dynamic ARX and the feed-forward neural network in case 2 are used for comparison.Table 5 shows that the MLQPR method can obtain higher mean accuracy than that in the image analysis model,the mathematic model,the dynamic ARX and the feed-forward neural network in the SVI predicting.The results demonstrate that the proposed MLQPR featuring higher predicting performance can be effectively applied for the sludge bulking risks in the WWTPS.

Moreover,predicting sludge bulking in this way can give accurate results(see Tables 3,4 and 5).It can be used to prevent sludge bulking,and ensure the effluent quality during sewage treatment operation process in time.The results demonstrate that the SVI trends in WWTP can be predicted with acceptable accuracy using the DO,F/M,Rr,SRT and TEM data as model input variables.

4.Conclusions

In this paper,a data-driven model,based on the MLQPR method,is proposed to predict the SVI values.The proposed MLQPR model is able to describe the relationship between SVI and the relative variables,as well as adjust the weights of model to improve the accuracy.Then,a real SVI predicting system,using the MLQPR model,is developed.Based on the results,the key findings of this study can be summarized as:

(1)A novel method—the MLQPR model,combining the MQPR method and the LLR method is developed to describe the nonlinear and complicated relationships between SVI and the variables of DO,F/M,SRT,Rr and TEM with a certain interference immunity.

(2)This proposed MLQPR model is able to update the regression coefficient onlineviahypothesis test.Therefore,this proposed MLQPR model can predict the SVI values with suitable accuracy.

(3)The results indicate that the proposed MLQPR model is a robust and effective model for predicting the SVI values.Furthermore,the proposed system with MLQPR is successfully applied in a real WWTP,which is essential to develop an efficient controller according to the predicting results.

[1]R.Dewil,J.Baeyensa,R.Goutvrind,The use of ultrasonics in the treatment of waste activated sludge,Chin.J.Chem.Eng.14(1)(2006)105-113.

[2]A.D.Kotzapetros,P.A.Paraskevas,A.S.Stasinakis,Design of a modern automatic control system for the activated sludge process in wastewater treatment,Chin.J.Chem.Eng.23(8)(2015)1340-1349.

[3]X.Flores-Alsina,J.Comas,I.Rodriguez-Roda,K.V.Gernaey,C.Rosen,Including the effects of filamentous bulking sludge during the simulation of wastewater treatment plants using a risk assessment model,Water Res.43(18)(2009)4527-4538.

[4]M.Laureni,D.G.Weissbrodt,I.Szivák,O.Robin,J.L.Nielsen,E.Morgenroth,A.Joss,Activity and growth of anammox biomass on aerobically pre-treated municipal wastewater,Water Res.80(1)(2015)325-336.

[5]J.Wang,Q.Li,R.Qi,V.Tandoi,M.Yang,Sludge bulking impact on relevant bacterial populations in a full-scale municipal wastewater treatment plant,Process Biochem.49(12)(2014)2258-2265.

[6]W.Li,P.Zheng,Y.L.Wu,E.C.Zhan,Z.H.Zhang,R.Wang,Y.J.Xing,G.Abbas,B.S.Zeb,Sludge bulking in a high-rate denitrifying automatic circulation(DAC)reactor,Chem.Eng.J.240(6)(2014)387-393.

[7]J.Wang,R.Qi,M.Liu,Q.Li,H.Bao,Y.Li,S.Wang,V.Tandoi,M.Yang,The potential role ofCandidatus Microthrix parvicellain phosphorus removal during sludge bulking in two full-scale enhanced biological phosphorus removal plants,Water Sci.Technol.70(2)(2014)367-375.

[8]I.Lou,Combination of respirometry and molecular approach for re-evaluating microbial kinetic selection of filamentous bulking in wastewater treatment system,Adv.Sci.Lett.9(1)(2012)540-544.

[9]P.H.Nielsen,P.Roslev,T.E.Dueholm,J.L.Nielsen,Microthrix parvicella,a specialized lipid consumer in anaerobic-aerobic activated sludge plants,Water Sci.Technol.46(1-2)(2002)73-80.

[10]H.Han,J.F.Qiao,Prediction of activated sludge bulking based on a self-organizing RBF neural network,J.Process Control22(6)(2012)1103-1112.

[11]M.Tampus,A.Martins,L.M.Van,The effect of anoxic selectors on sludge bulking,Water Sci.Technol.50(6)(2004)261-268.

[12]J.H.Choi,H.L.Sang,K.Fukushi,K.Yamamoto,Comparison of sludge characteristics and PCR-DGGE based microbial diversity of nanofiltration and micro filtration membrane bioreactors,Chemosphere67(8)(2007)1543-1550.

[13]M.Eschenhagen,M.Schuppler,I.Röske,Molecular characterization of the microbial community structure in two activated sludge systems for the advanced treatment of domestic effluents,Water Res.37(13)(2003)3224-3232.

[14]A.A.Zinatizadeh,A.R.Mohamed,M.D.Mashitah,A.Z.Abdullah,I.M.Hasnain,Characteristics of granular sludge developed in an up- flow anaerobic sludge fixedfilm bioreactor treating palm oil mill effluent,Water Environ.Res.79(8)(2007)833-844.

[15]A.M.Martins,K.Pagilla,J.J.Heijnen,M.C.van Loosdrecht,Filamentous bulking sludge:a critical review,Water Res.38(4)(2004)793-817.

[16]S.M.Kotay,T.Datta,J.Choi,R.Goel,Biocontrol of biomass bulking caused byHaliscomenobacter hydrossisusing a newly isolated lytic bacteriophage,Water Res.45(1)(2011)694-704.

[17]I.Lou,Y.C.Zhao,Sludge bulking prediction using principle component regression and artificial neural network,Math.Probl.Eng.583(3)(2012)295-308.

[18]D.P.Mesquita,O.Dias,A.M.A.Dias,A.L.Amaral,E.C.Ferreira,Correlation between sludge settling ability and image analysis information using partial least squares,Anal.Chim.Acta642(1)(2009)94-101.

[19]M.G.Adonadaga,Effect of dissolved oxygen concentration on morphology and settle ability of activated sludge flocs,J.Appl.Environ.Microbiol.3(2)(2015)31-37.

[20]D.L.Giokas,G.T.Daigger,M.von Sperling,Y.Kim,P.A.Paraskevas,Comparison and evaluation of empirical zone settling velocity parameters based on sludge volume index using a unified settling characteristics database,Water Res.37(16)(2003)3821-3836.

[21]E.Ramin,D.S.Wágner,L.Yde,P.J.Binning,M.R.Rasmussen,P.S.Mikkelsen,B.G.Plósz,A new settling velocity model to describe secondary sedimentation,Water Res.66(1)(2014)447-458.

[22]D.Jassby,Y.Xiao,A.J.Schuler,Biomass density and filament length synergistically affect activated sludge settling:systematic quantification and modeling,Water Res.48(1)(2014)457-465.

[23]I.Y.Smets,E.N.Banadda,J.Deurinck,N.Renders,R.Jenné,J.F.van Impe,Dynamic modeling of filamentous bulking in lab-scale activated sludge processes,J.Process Control16(3)(2006)313-319.

[24]M.Bagheri,S.A.Mirbagheri,Z.Bagheri,A.M.Kamarkhani,Modeling and optimization of activated sludge bulking for a real wastewater treatment plant using hybrid artificial neural networks-genetic algorithm approach,Process Saf.Environ.Prot.95(1)(2015)12-25.

[25]H.Han,J.Qiao,Hierarchical neural network modeling approach to predict sludge volume index of wastewater treatment process,IEEE Trans.Control Syst.Technol.21(6)(2013)2423-2431.

[26]H.Han,Q.Chen,J.Qiao,An efficient self-organizing RBF neural network for water quality prediction,Neural Netw.24(7)(2011)717-725.

[27]S.Yin,S.X.Ding,X.Xie,H.Luo,A review on basic data-driven approaches for industrial process monitoring,IEEE Trans.Ind.Electron.61(11)(2014)6418-6428.

[28]H.Haimi,M.Mulas,F.Corona,R.Vahala,Data-derived soft-sensors for biological wastewater treatment plants:an overview,Environ.Model.Softw.47(1)(2013)88-107.

[29]J.M.Brault,R.Labib,M.Perrier,P.Stuart,Prediction of activated sludge filamentous bulking using ATP data and neural networks,Can.J.Chem.Eng.89(4)(2011)901-913.

[30]Q.Q.Tian,J.J.Chen,J.K.Dong,A method of constructing the fuel efficiency model based on quadratic polynomial regression,Procedia Eng.15(1)(2011)3749-3753.