面向导航星座的混合路由技术研究
张 方,周 淦,喻瑶瑶,聂殿辉,丰大军
(1. 中国电子信息产业集团有限公司第六研究所,北京 100083;2. 西安电子科技大学 空间科学与技术学院,陕西 西安 710071)
0 引言
随着卫星应用和需求的不断发展,卫星导航系统无论是在战略资源上还是商务民用方面都体现了其重要的应用价值,给人们的工作和生活带来很大的便利。然而,由于传统的卫星导航系统存在导航精度低、抗毁性能差和无自主运行能力等缺点,已无法满足人们对卫星业务的需求。星间链路的建立则可以很好地解决以上问题,它不仅可以实现各节点(不同轨道的卫星与地面站)之间的互联互通,还帮助形成具有对空间传输信息的获取、存储、处理、传输以及分发等功能的空间信息网络,是卫星导航系统的必然发展方向[1-4]。
近年来,全球卫星导航系统飞速发展并不断完善,星间链路的引入给导航系统带来较多的技术难题,其中,路由规划问题成为研究的焦点。国内外学者对于导航系统的路由规划问题也有大量的研究成果可以借鉴。文献[5]对星间可见性以及星间距离变化做了详细分析,根据推导出的公式设计了一种静态无需切换和一种动态带切换的网络拓扑结构;文献[6]针对同轨道星间链路拓扑结构进行分析,通过对比不同的拓扑结构对星地数据传输性能的影响,得出当数据在节点处理时延较大时同轨链路应选择八角星拓扑结构的结论;文献[7]基于TDMA时分多址体制的星间通信模式提出了一种较为全面的通信代价评估方案,得出星间链路混合型拓扑结构比环形拓扑结构的通信性能更好的结论。
针对以上研究现状,本文面向导航星座,研究包含卫星网络所组成的天基网和各地面站所组成的地基网络的多层空间网络路由规划问题,提出了一种混合路由方案。首先对节点负载和传输距离等影响数据传输的因素进行单独研究,然后综合考虑等待时延、链路速率、节点负载和传输距离等多种影响因素,探索并建立合理的混合评价函数,使算法所规划出的路径能够减小复杂的空间运行环境对信息传输的影响,合理有效地利用星间链路资源,从而增强系统的稳定性和可靠性,为正在建设过程中的“北斗”卫星导航系统提供理论依据和应用基础。
1 星座拓扑分析
1.1 星座构型
本文研究的空间网络模型分为3层,包括高轨卫星、中轨卫星和地面站以及地面控制管理中心。其中,高轨卫星高度约36 000 km,由3颗GEO和3颗IGSO构成,GEO分布在赤道上,经度分别为80°、110.5°和140°;IGSO轨道倾角为55°,三星相位差120°。中轨卫星MEO由构型为Walker24/3/1星座构成,轨道高度为21 528 km,为了便于分析,将24颗MEO卫星分别命名为MEOij(i∈[1,3],表示轨道面编号;j∈[1,8],表示轨道内的卫星编码)。地面由3个地面站和1个地面控制管理中心构成,分布于我国境内,其中,地面控制管理中心通过对地面站合理的规划与调度实现对卫星的监测与控制。导航星座整体架构如图1所示。
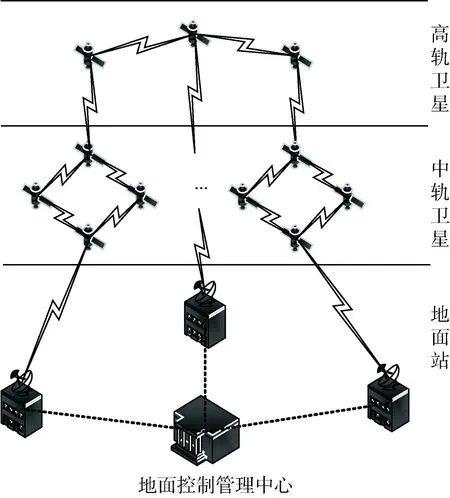
图1 导航星座构型示意图
1.2 星间可视性分析
卫星之间的可视性是星间通信的前提条件。目前影响卫星之间的可视因素主要包括地球及大气层的遮挡、卫星天线波束扫描范围限制以及电磁波测距极限3个方面,下面作详细介绍。
(1)地球及大气层的遮挡
假设地球半径为R,卫星轨道高度为h,大气层厚度为H,卫星A、B之间的距离为l,如图2所示。
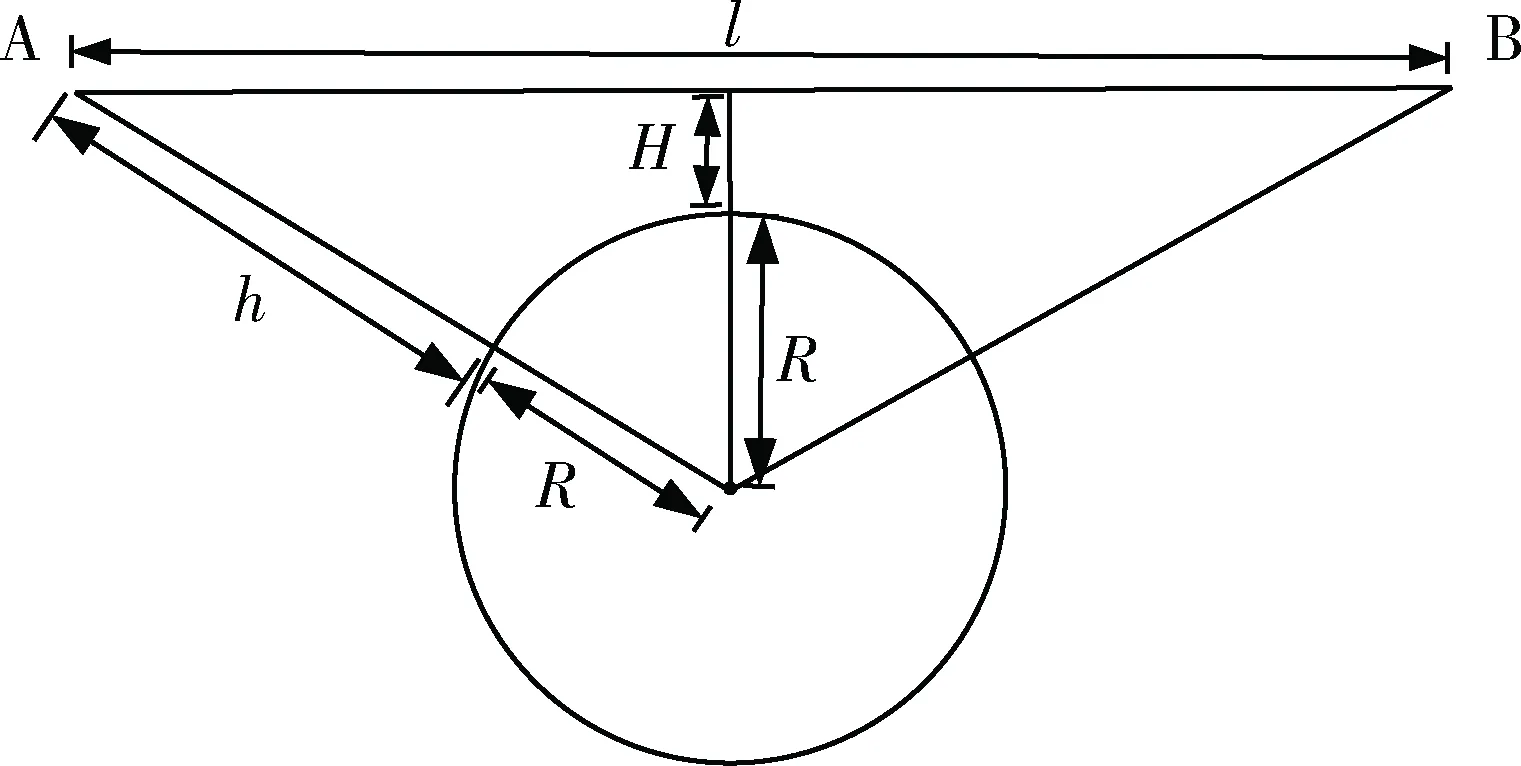
图2 地球遮挡情况下卫星可见关系示意图
由几何关系可得卫星之间的距离l应满足如下关系式:
(1)
(2)卫星天线波束扫描范围限制
假设地球半径为R,卫星轨道高度为h,两卫星之间的距离为l,波束扫描范围为±β,如图3所示。

图3 卫星波束扫描范围受限情况下可见关系示意图
由几何关系可得卫星之间的距离l应满足如下关系式:
l>2(R+h)cosβ
(2)
综上所述,两卫星之间建立通信的前提条件为它们之间的距离l应满足如下关系式:
(3)
(3)电磁波测距极限
卫星A、B要能够建立链路进行通信,除了满足以上两个条件外,还必须满足两者之间的距离小于电磁波所能达到的最大距离,即:
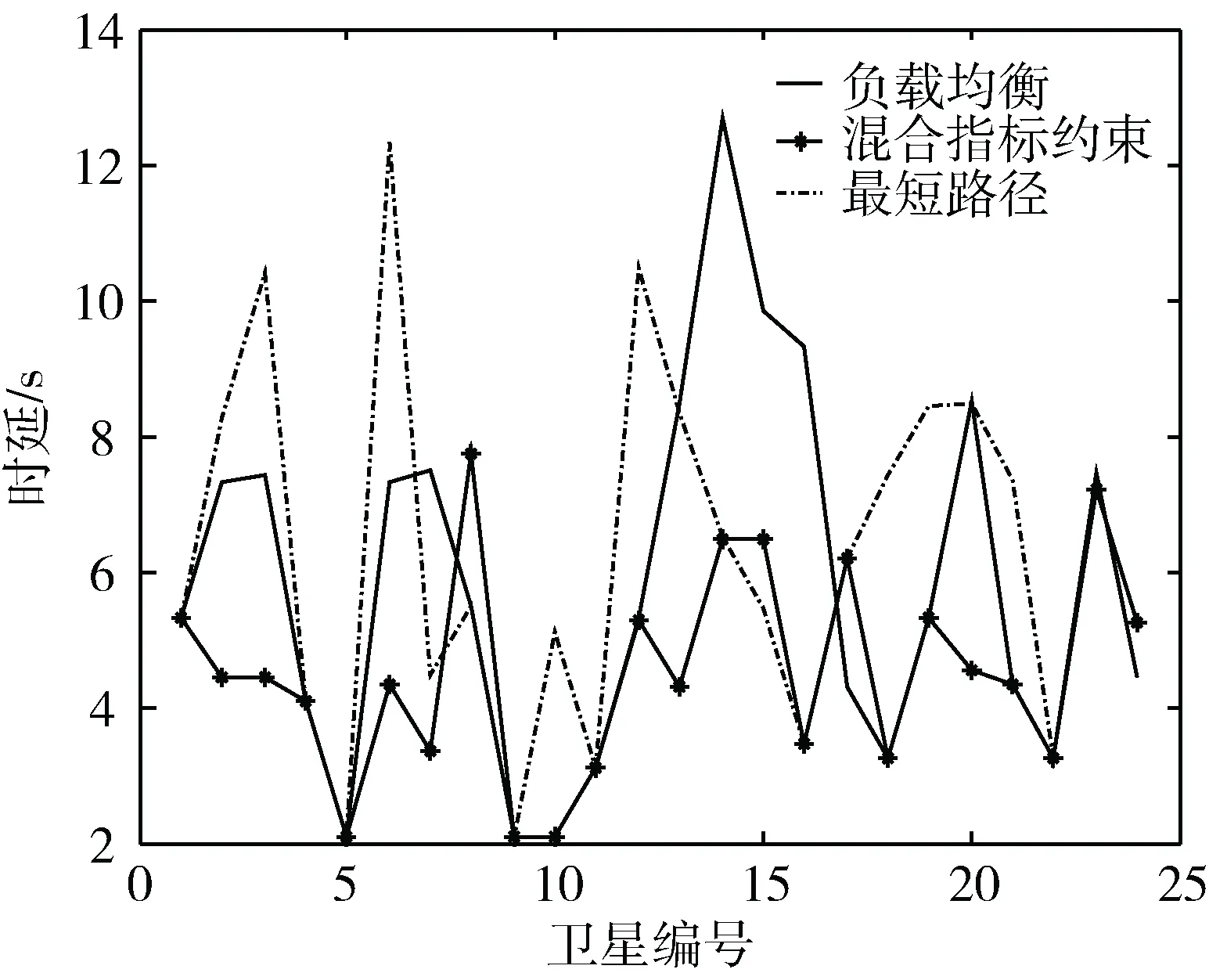
l (4) 式中,Lmax为测距极限,本文取Lmax=5 000 km。 因此,星间链路可见性可表述为:如果卫星A、B之间的连线与地球表面(考虑大气层)没有交点,接收星在发射星的天线覆盖范围内,且在发射星的测距范围内,则称两颗星是可见的;否则,如果缺少任何一个或几个条件,则称它们是不可见的。因此卫星B对卫星A的可见性VB→A定义为:VB→A=1,交点不存在,即可见;VB→A=0,交点存在,即不可见。由此,可以确定一个瞬时的拓扑结构。 星间链路有3种,包括永久链路、非永久链路和不可见链路,分别对应卫星持续可见、非持续可见和永远不可见3种情况。对于导航星座来说,频繁地切换拓扑结构对于系统的稳定性是不利的,因此建立如下建链规则: (1)优先与永久链路建链,尽量减少网络拓扑结构的切换频度。 (2)采用在永久链路的基础上增加非永久链路的组合方式建链,以避免链路性质过于单一导致拓扑结构的抗毁性降低。 通过使用卫星工具包(Satellite Tools Kit, STK)对星座进行仿真,得到卫星的永久链路有6条,包括同轨道中和本星相隔的2颗卫星,西侧相邻轨道与目标星平近点角相差-15°、-150°的2颗卫星以及东侧相邻轨道与目标星平近点角相差15°、150°的2颗卫星。 对于非永久链路的选取,则采用GDOP贡献值法,将除永久链路之外的可视卫星进行GDOP贡献值排序,选取GDOP贡献值较大的卫星进行建链,以保证导航星座的测量精度,提高导航服务质量。本文中非永久链路为5条[8]。 路由生成方案的设计要解决的问题是:针对特定场景,从多条备选路径中搜索出最佳路由方案。通常,为链路设置一个权值来反映该链路的数传代价,进而通过选择权值最小的链路进行最优路由的生成。本文针对链路权值展开重点分析,而在路径搜索上则沿用传统的Dijkstra算法。 Dijkstra算法的基本思想是:以路径长度为对应路径的权值,通过对权值的迭代,得到从源节点到目的节点的最小权值对应的最短路径[9]。代码如下: Dijkstra算法:function Dijkstra(G, w, s) 输入: 邻接矩阵G,起始节点w,目的节点s 输出: 最短路径对应的节点及权值 for (each vertex v in V[G]){ d[v]:= infinity //将各点的已知最短距离设成无穷大 previous[v]:= undefined } d[s]:= 0 //将s到s的最小距离设为0 S:= empty set Q:= set of all vertices while (Q is not an empty set){ u:= Extract_Min(Q) S.append(u) for (each edge outgoing from u as (u,v)){ if d[v] > d[u] + w(u,v) d[v]:= d[u] + w(u,v) previous[v]:= u } } 通过使用Dijkstra算法即可搜索出源节点到目的节点的最短路径。在实际的卫星导航系统中,地面控制管理中心即可通过该路径对全网卫星进行遥测回收或境外星指令上注,具有实际应用价值。 传统的路由生成方法对于数传的影响因素考虑较为单一,如最短路径算法以距离作为数传代价进行路径搜索,算法可以搜索出源节点到目的节点距离最短的路径,但不能保证时延最小,实际上卫星从接收信息到发射信息期间的时延是不容忽视的。因此,传统的路由算法难以满足实际工程应用的需求。 本文在减小端到端时延和均衡节点负载方面,对影响因素进行较为全面的分析。其中,端到端时延主要包括等待时延(卫星从接收到发送期间的等待时间)、链路传输速率所产生的时延以及节点空间距离产生的传播时延。同时,为了充分高效地利用空间网络资源,算法会首先计算各节点的负载,然后再进行路由规划,并尽可能使各节点的负载均衡化,来降低网络出现拥塞或者丢包的可能性,从而保障系统能够稳定运行。因此,本文考虑的数传代价包括[10]:(1)等待时延;(2)链路速率;(3)节点距离;(4)节点负载。 节点距离、节点负载以及等待时延与数据传输代价成正比,而链路速率越大,数据传输所消耗的时间就越短,因此链路速率与数据传输代价成反比。结合以上因素,本文给出链路权值Q的定义如下[11]: (5) 其中,ρ为链路长度,ρmax为当前时刻所有能够进行通信的节点之间的距离的最大值;l为节点的负载,lmax为当前所有节点负载的最大值;t_wait为下一跳节点的等待时延,t_waitmax为全网节点等待时延的最大值;r为节点之间的信息传输速率,考虑到真实系统中链路传输速率的可选性,本文中星间传输速率包含4组可选值,而星地传输速率包含2组可选值,rmax为当前正在进行通信的所有卫星间的最大信息传输速率。将式(5)中的各因素进行归一化处理可以更客观公平地反映链路代价。 本实验采用典型的遥测回传及数据上注的业务场景,实现地面控制管理中心对24颗中轨道卫星的实时监测和控制。地面站不可直接观察到的卫星为境外星;反之,则为境内卫星。两种卫星与地面控制管理中心的数据传输都需要对地面站进行规划与调度,另外,对于境外卫星而言,还要选择合适的节点星进行数据中转。因此,要求路由算法能够规划出一条合理的路径,使得卫星与地面控制管理中心的通信时延应尽可能小,同时要保证各节点的负载指数差在可接受范围内。本实验仿真时刻为2017年10月13日4:00:00am,假设每颗卫星所产生的遥测数据量相等(GEO/IGSO除外),图例中卫星编号1~24分别对应MEO11~MEO38。 实验首先将最短路径路由算法和所提出的混合指标约束的路由算法得出的结果进行对比,来验证混合指标约束方案能够从当前满足建链条件的卫星中选择距离较近的卫星来建链;然后,将负载均衡路由算法和混合指标约束路由方案得出的结果进行对比,验证混合路由方案能从满足建链条件的卫星中选择当前时刻较为空闲的卫星进行数据传输;最后,将3种算法得到的路由方案时延进行对比,验证混合路由方案可以在综合多种影响因素的情况下为卫星计算出时延最小的路由,从而确保地面控制管理中心对卫星监测和遥控的实时性。下面对仿真结果进行详细介绍。 3.2.1混合路由方案路径最短验证 将最短路径路由算法和混合路由方案所规划的路径进行进一步整理,得到两种算法的链路距离,结果如图4所示。 图4 源节点到目的节点路径的距离 从图4中可以看出,混合路由方案在大部分情况下得到的结果与最短路径算法得到的结果接近,只有在个别处出现较大的差距,这是因为混合路由方案选择了使得遥测回传时延最小的路径而没有选取最短路径所致,并且通过3.2.3节可以看出这并不影响混合路由方案选择出时延最小的路径。 3.2.2混合路由方案负载均衡验证 将负载均衡算法和混合路由方案下各节点的负载情况进行了统计,统计结果如图5所示。 图5 卫星负载 从图5可以看出两种算法各节点的负载均衡度相差不大,混合路由方案在卫星MEO17、MEO26处负载稍大,这种情况是符合最优化理论的。为此进一步计算出了所有节点负载指数的方差以定量分析均衡度。负载均衡算法各节点负载指数方差为0.022,混合路由方案下各节点负载指数方差为0.029,由此可以得到结论:混合路由方案能够从满足建链条件的卫星中选择相对空闲的卫星建立链接,以达到负载均衡的目的。值得指出的是,两种算法负载指数在卫星MEO14、MEO15、MEO21、MEO22和MEO23处均出现峰值,这是由于当前时刻这些卫星节点作为境内接入卫星所导致的。 3.2.3混合路由方案最小时延验证 对于路由算法,其所规划的路径具有较小的时延是至关重要的。为了进一步验证混合路由方案能够规划出时延较小的路径,将最短路径和负载均衡路由算法同本文提出的混合路由方案所规划的路径时延进行了统计分析,统计结果如图6所示。 图6 卫星数据下传到地面站时延 图6是最短路径算法、负载均衡算法和混合路由方案下, 24颗MEO将数据下传到地面站的时延统计图。从图中可以看出,混合路由方案所规划的路径时延在大部分情况下都是小于其他两种算法的。这是由于在一些特殊情况下,为了使各节点负载相对均衡,算法选择了等待时延或者距离稍大的卫星作为中转卫星所致,但该路径时延仍在可接受范围内。同样,在卫星MEO14、MEO15、MEO21、MEO22和MEO23处,各方案所规划路径时延相等是该卫星和地面站的可见性导致的。 本文首先简要分析了星间链路拓扑结构模型,引出卫星导航系统的路由问题;然后,提出了一种综合考虑等待时延、链路速率、节点负载和传输距离等多种影响因素的混合路由策略;最后,以端到端时延和节点负载为评价指标,通过实验验证了本文所提出的混合路由策略大部分情况下能够在保证网络负载均衡的同时,搜索出端到端时延最小的路径,合理有效地利用星间链路资源,为正在建设过程中的北斗全球卫星导航系统提供理论依据和应用基础。 [1] LUBA O, BOYD L, GOWER A, et al. GPSIII system operations concepts[J]. Position Location and Navigation Symposium, 2004, 20(1):354-363. [2] RAJAN J A. Highlights of GPSII-R autonomous navigation [C]//Proceedings of the ION 58th Annual Meeting of the Institute of Navigation and CIGTF 21st Guidance Test Symposium. Albuquerque, NM:The Institute of Navigation, Inc, 2002:354-363. [3] HOLMES J K, RAGHAVAN S. A summary of the new GPS IIR-M and IIF modernization signals[C]//Proceedings of the Vehicular Technology Conference (VTC 2004-fall). Los Angeles: IEEE, 2004:4116-4126. [4] 刘小跃.空间信息网高性能路由协议研究[D]. 西安:西安电子科技大学,2012. [5] 李振东,何善宝,刘崇华,等,一种导航星座星间链路拓扑设计方法[J].航天器工程,2011,20(3):32-37. [6] 侯颖,米志超,于卫波,等,星地一体化导航系统星间链路仿真分析[J].通信技术,2014, 47(2):145-149. [7] 陈建云,吴光耀,冯旭哲,等,卫星星座星间通信链路拓扑分析[J].仪器仪表学报,2014, 35(12):101-105. [8] 周淦,张方,喻瑶瑶,等,导航星座星间链路拓扑及混合路由方案[C].北京:中国卫星导航学术年会,2018. [9] 张美玉,简琤峰,侯向辉,等.Dijkstra算法在多约束农产品配送最优路径中的研究应用[J]. 浙江工业大学报,2012, 40(3):321-325,330. [10] 王冬霞,赵金贤,胡彩波,等.双层卫星网星间链路混合路由算法设计 [J]. 导航定位学报,2016, 4(2):29-35. [11] 孙娟.导航星座星间链路设计研究[D]. 南京:南京航空航天大学,2011.1.3 卫星拓扑模型
2 路由方案的设计
2.1 概述
2.2 Dijkstra算法描述
2.3 混合路由策略
2.4 链路权值的定义
3 仿真结果
3.1 仿真场景
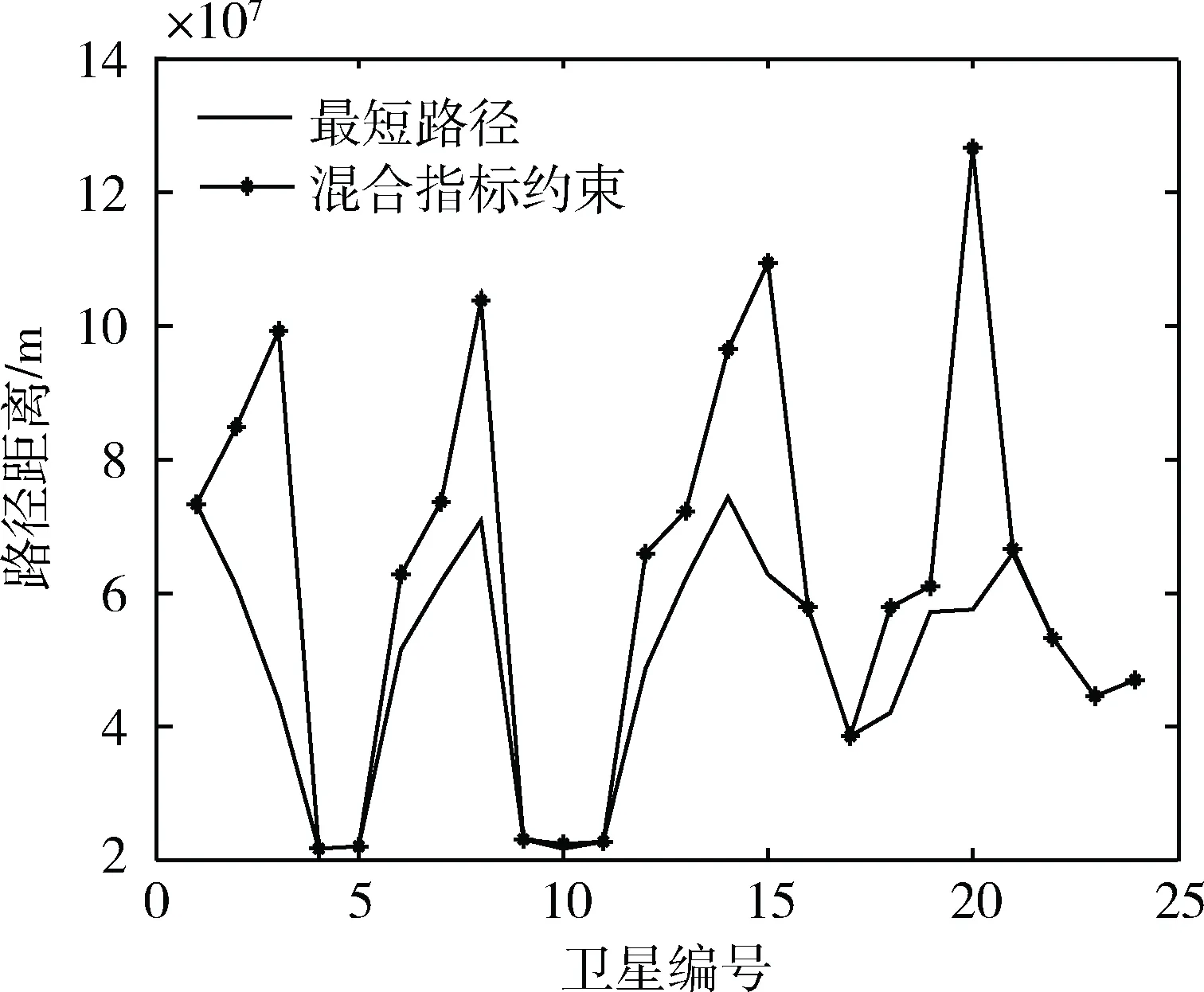
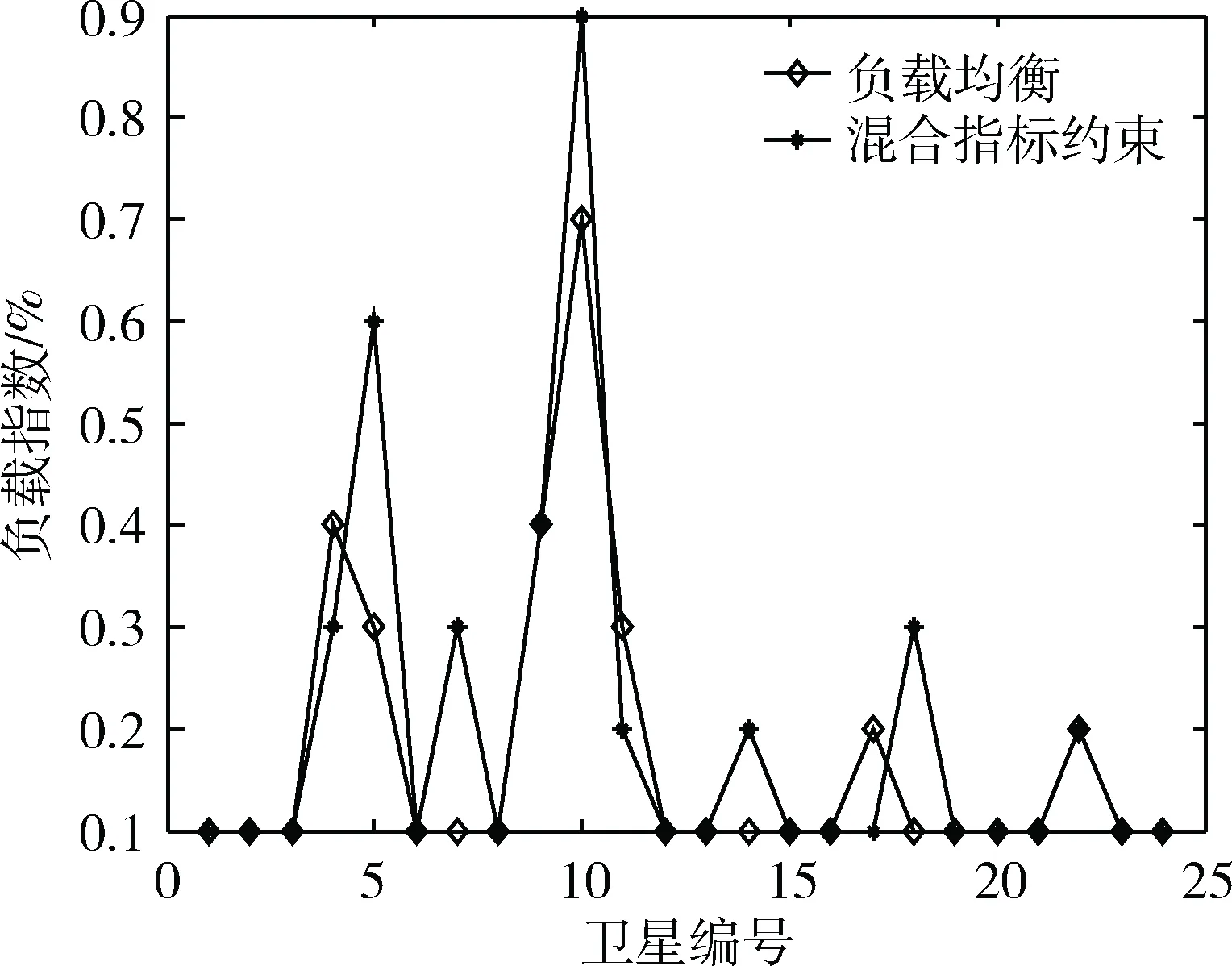
3.2 实验结果
4 结论

