基于粒子滤波的锂电池SOC二次滤波算法*

邢云凤，赵 野

(1. 中国科学院微电子研究所 新能源汽车电子研发中心，北京 100029；2.中国科学院物联网研究发展中心，江苏 无锡 214135；3.中国科学院大学，北京 100049)

0 引言

人们环保意识的提高以及国家政策的大力支持，使得电力取代燃油作为汽车的主要动力成为可能。而动力电池的不安全性、电池科技的不完善却成为限制新能源汽车行业发展的瓶颈。SOC估计是电池状态估计的核心，其定义为电池剩余容量占电池容量的比值[1]。准确的SOC估计不只是计算电池电量和续航能力，还能反映电池的工作状态，为电池组均衡提供基础，从而提高安全性和延长电池寿命。然而,实际的工况复杂度使得SOC呈现非线性，这对SOC的估计算法提出了很高的要求。

卡尔曼滤波器(Kalman Filter, KF)是线性最优滤波器,常被用于估算电池的SOC。由于系统的非线性，拓展卡尔曼滤波(Extended Kalman Filter, EKF)将非线性系统方程进行一阶泰勒展开实现近似线性滤波，但在非线性程度较高的应用场景下，算法因忽略了高阶泰勒因子而发散。无迹卡尔曼滤波(Unscented Kalman Filter, UKF)在卡尔曼滤波基础上提高了非线性近似度，但依然不能准确地描述系统的非线性。为了更好地描述系统的非线性，粒子滤波(Particle Filter, PF)通过粒子的分布情况反映系统状态，从而实现了非线性非高斯系统的精准滤波。但是在观测误差较大的情况下，误差分布会对粒子集选择造成很大的干扰。拓展卡尔曼粒子滤波(Extended Kalman Particle Filter, EKPF)通过EKF方法产生粒子滤波的建议分布，可以提高粒子滤波的估计精度，但因为要对每个粒子进行EKF滤波，使得算法复杂度剧增，对BMS的硬件条件要求很高。

在一定的复杂度要求下，本文基于改进PNGV(the Partnership for a New Generation of Vehicles)模型，实现了模型参数的在线实时更新，将粒子滤波与卡尔曼滤波相结合，应用卡尔曼滤波对粒子滤波结果进行再滤波处理，从而大大减小粒子滤波误差、提高算法精确度。通过仿真实验表明，该二次滤波算法(Kalman Particle Dual Filter, KPDF)在计算复杂度几乎不变的前提下，精确度相较EKF算法、PF算法有明显的提高。

1 改进PNGV模型

SOC的不可观测性使得电池模型对SOC具有十分重要的意义。PNGV电池模型具有良好的动态特性，在不断变化的实际工况中，PNGV模型可以更好地模拟电池特性。在对磷酸铁锂电池的阻抗谱研究中发现，磷酸铁锂电池阻抗的Nyquist图有两个半圆，也就是其具有两个极点，对应于电池模型有两个时间常数。因此，在PNGV模型基础上添加一个RC环路可以更好地反映电池极化特性。

图1为改进的PNGV模型，E为电压源，电容Cb用来描述电流累积引起的开路电压变化，E和Cb构成开路电压OCV。Ro为电池直流内阻，两个RC环路用来描述电池的极化效应。由基尔霍夫定律可以得到PNGV数学模型为：

UL=OCV-Up1-Up2-ILRO

(1)

(2)

(3)

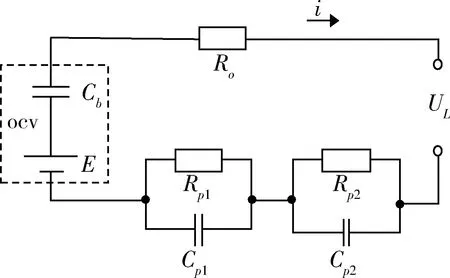
图1 改进PNGV模型

2 模型参数的实时更新

在实际工况中，电池模型参数会受温度、充放电倍率、循环次数等因素影响而发生变化，使得电池模型参数不能很好地反映实际工况，而SOC估计算法的精确度非常依赖于电池模型的精度。因此，本文采用含有遗忘因子的递推最小二乘算法，结合OCV-SOC曲线可以实现模型参数的在线更新。

设该线性系统的输入输出模型为:

y(k)+a1y(k-1)+a2y(k-2)=b0x(k)+

b1x(k-1)+b2x(k-2)

(4)

由电池PNGV模型可得：

(5)

其中τ1,τ2为时间常数。可得：

(6)

令y(k)=Uoc-UL，x(k)=I,可得系统输入输出方程为：

(7)

因此，若令观测矩阵:

h(k)=[-y(k-1)-y(k-2)x(k)x(k-

1)x(k-2)]

(8)

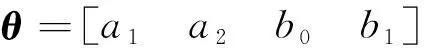
Ro=b0

(9)

(10)

(11)

(12)

(13)

(14)

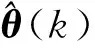
对于观测量y(k)，UL为输出电压，可直接测得。Uoc为开路电压(Open Circuit Voltage, OCV)不能实时测得，因为Uoc与SOC有一一对应的关系，所以可以在得到SOC的估计值后，通过OCV-SOC曲线得到OCV的值。

本文选用额定电压为3.2 V、额定容量为2 230 mAh的磷酸铁锂电池进行小电流充放电实验，得到充放电OCV-SOC曲线如图2所示。小电流充放电可以将极化电压降到最小，对充放电OCV取均值后可以在一定程度上起到消除极化电压的作用。

3 基于KPDF算法的SOC估计

针对拓展卡尔曼滤波与粒子滤波的优缺点，本文采用KPDF算法，该算法在系统具有线性状态方程和非线性观测方程的应用场景下具有很好的滤波效果。

3.1 粒子滤波阶段

本文中结合安时积分公式以及电池数学模型，可以得到系统的状态空间模型：

xk=Axk-1+Buk-1+wk-1

(15)

yk=OCV(Sk)-Up1k-Up2k-Roik+vk

(16)

为计算方便，选择最小均方误差准则求得系统状态的最优估计，用样本均值代替积分运算，粒子滤波的具体递推过程如下：

(1)初始阶段：用大量粒子模拟系统初始状态x0，起始权值w0均为1/N。

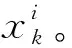
(17)

其中σ2为观测噪声的方差。对权值进行归一化得到：

(18)

选择高斯重要密度函数可以有效降低算法复杂度。

(4)重采样阶段：根据每个粒子归一化权值计算有效粒子数是否小于粒子数阈值，若小于则更新粒子集，其权值均为1/N，从而使得粒子分布逐渐趋向状态变量的后验概率密度函数。

(5)最小均方估计：依据最小均方误差准则

(19)

(6)令k=k+1，返回步骤(2)继续循环。

3.2 卡尔曼滤波阶段

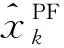
因此，得到系统状态间模型为：

xk=Axk-1+Buk-1+wk-1

(20)

(21)

状态估计初值设为初始粒子滤波估计结果，即：

(22)

结合电池模型参数的在线辨识，得到SOC估计的总流程如图3所示。

图3 模型参数与SOC联合估计流程图

4 算法仿真及分析

为验证参数在线识别以及本文提出的SOC估计算法的优越性，利用额定电压为3.2 V、额定容量为2 230 mAh的磷酸铁锂电池进行实验，实验工况选用美国联邦城市驾驶工况FUDS。经模型参数在线识别后，得到的输出电压与实际工况电压对比图如图4所示。

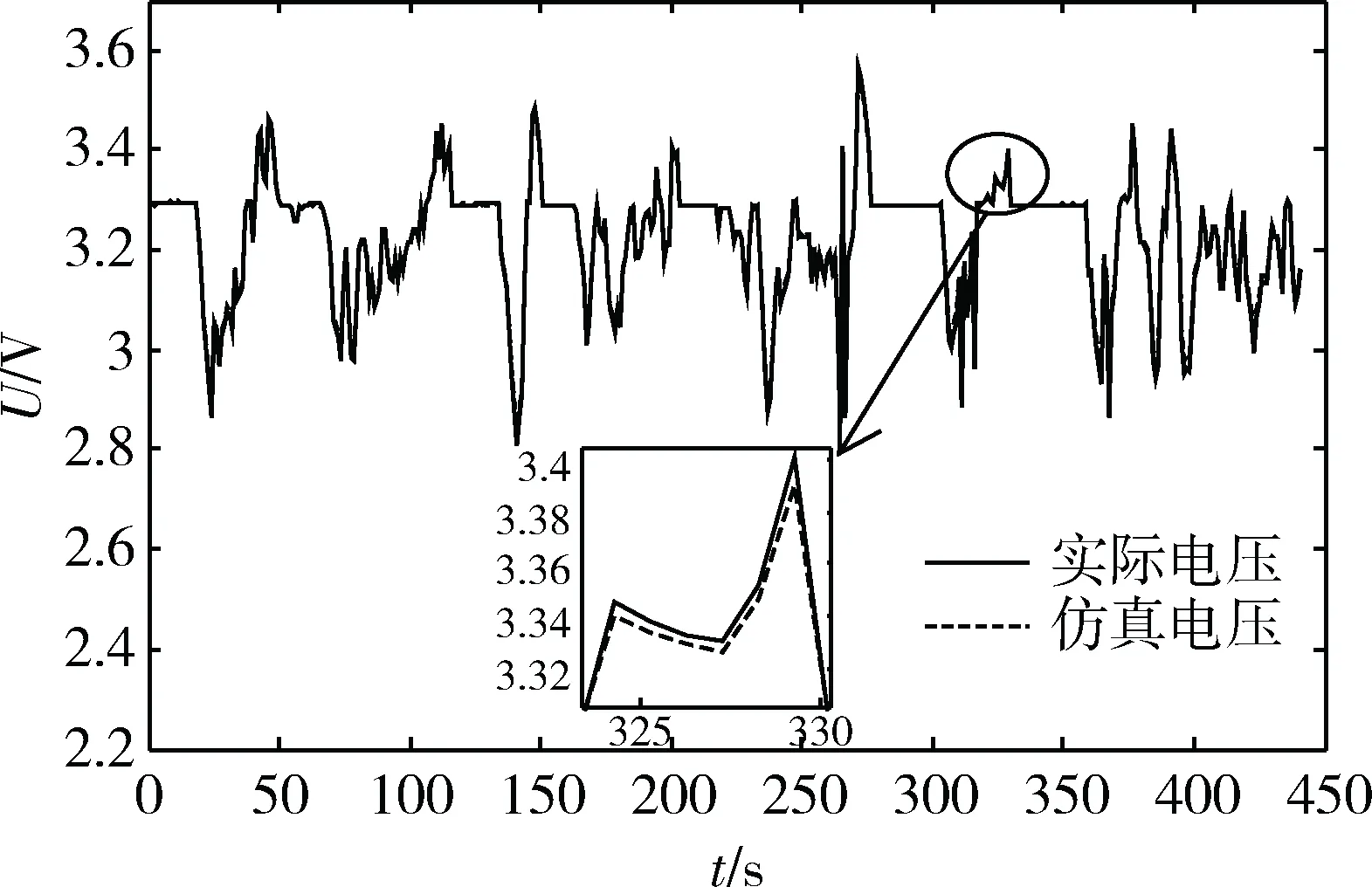
图4 FUDS工况仿真电压对比

将在线识别参数模型与离线方法进行对比，误差曲线如图5所示。模型参数在线辨识得到的输出电压误差在0.03 V以内，而离线误差在0.25 V以内。参数在线辨识可以使模型精度大幅提高，为SOC估计提供了准确的模型基础。

图5 输出电压误差

在此模型基础上，对本文提出的KPDF算法进行验证。图6为采用PF、EKF、EKPF以及本文提出的KPDF算法计算得到的SOC估算值与真实值的对比图(粒子数N均取50)。从图中可以看出，本文算法相较其他三种算法具有更好的精准度。

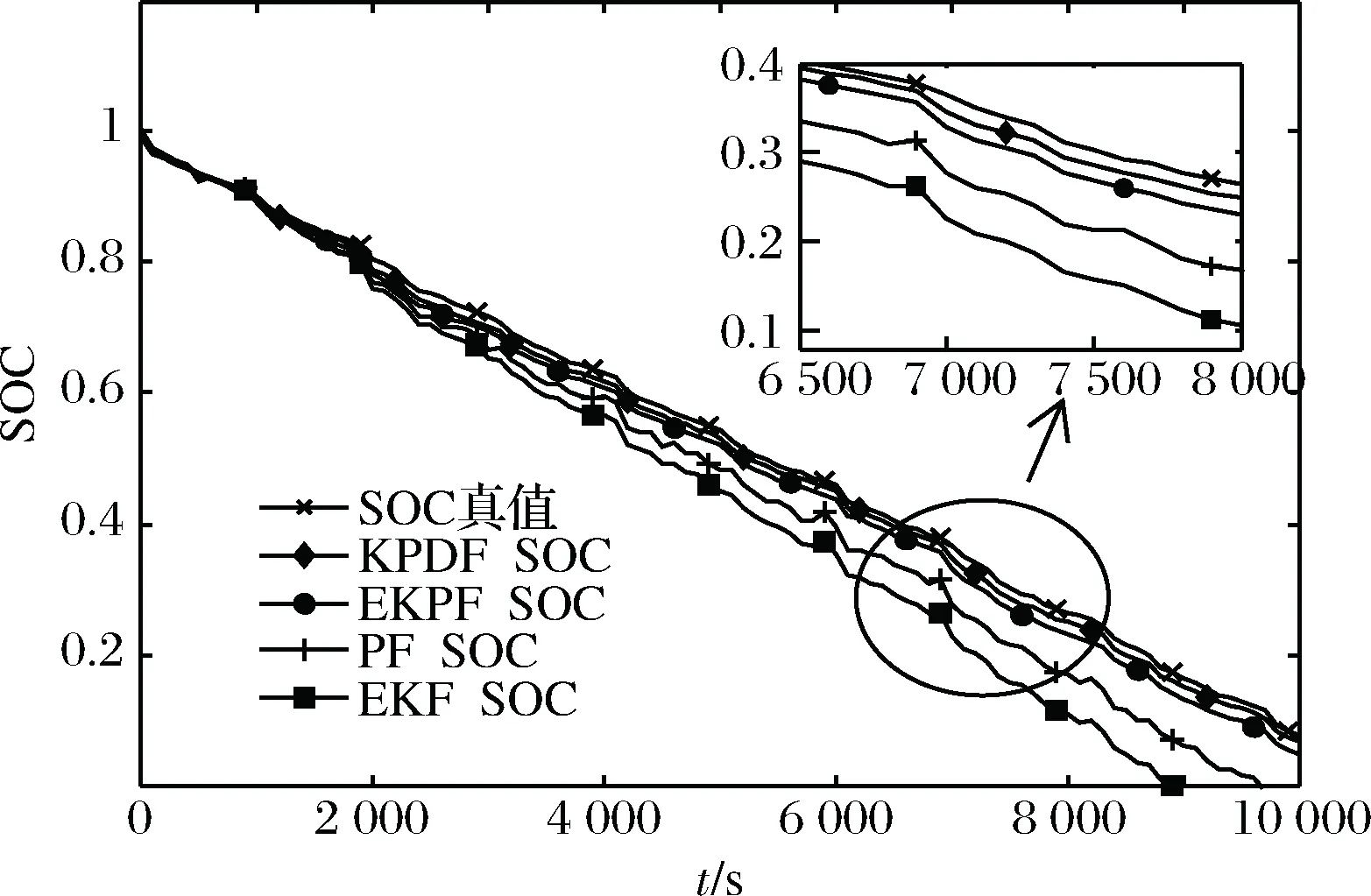
图6 几种SOC估计算法对比

为综合考虑算法的时间复杂度、精确度和纠错能力，本文计算了几种算法的最大误差、均方误差，并利用MATLAB的Profile功能对算法运行时间进行统计。另外，为对算法的收敛性进行验证，将SOC起始值由0.9设为0.7，记录算法估计值收敛到真值±4%内的时间(以实际实验对应时间为准)，得到对比结果如表1所示。

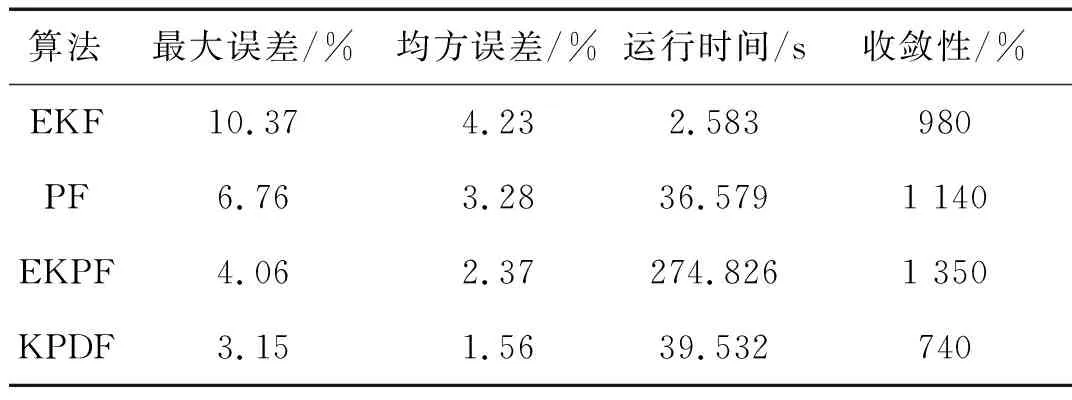
表1 几种常用算法性能比较

可以看出，EKPF算法虽然提高了精确度，但运算量大。而本文提出的KPDF算法是对整体粒子滤波结果进行二次滤波，滤波精度远高于EKF和PF算法，但算法复杂度相较粒子滤波并未明显提高。算法在准确度、计算复杂度、收敛性方面都有着优秀的表现。

5 结论

本文基于参数在线识别的改进PNGV电池模型，提出了对SOC的粒子滤波结果进行卡尔曼二次滤波的KPDF算法，并实现了模型参数与SOC的实时联合估计。实验证明，KPDF算法在接近PF算法计算量的前提下，精确度相较EKF算法、PF算法具有明显提高。

[1] 麻友良,陈全世,朱元.变电流下的电池荷电状态定义方法探讨[J].电池,2001,31(1):7-9.

[2] Xiong Rui, He Hangwei, Zhao Kai. Research on an online identification algorithm for a thevenin battery model by an experimental approach[J]. International Journal of Green Energy, 2015, 12(3):272-278.

[3] Yang Fangfang, Xing Yinjiao, Wang Dong, et al. A comparative study of three model-based algorithms for estimating state-of-charge of lithium-ion batteries under a new combined dynamic loading profile[J]. Applied Energy,2016,164:387-399.

[4] Shao Sai. On-line estimation of state-of-charge of Li-ion batteries in electric vehicle using the resampling particle filter[J]. Transportation Research Part D,2014,32(32):207-217.