基于贝叶斯混合概率分布融合的系统可靠性分析与预测方法

杨乐昌, 郭艳玲

(1. 北京科技大学机械工程学院, 北京 100083;2. 北京航空航天大学自动化科学与电气工程学院, 北京 100191)

0 引 言

层次性结构模型是一类具有普遍适用性的模型。基于“从整体到局部”的系统工程思想,大部分复杂机电设备(如卫星),都可以视作多层次系统,自上而下通常可划分为系统层、子系统层,零部件层等,而其对应的可靠性模型通常也具有显著的层次性特征。在对这些可靠性模型进行分析,做出可靠性预测的过程中,需要面对的问题也与传统可靠性模型有较大差别。

一方面,复杂机电设备通常包含众多部件组件,作为底层的零部件多为标准件(如齿轮,轴等),通常已积累了较为充分的先验知识与实验数据,且有历史经验数据可供参考,认知较为完备;另一方面,对于系统整体而言,由于工况及实验条件所限,整体性实验一般代价高昂,开展难度大,特别是在一些涉及航空航天、核工业的重大设备,由于客观条件所限,几乎不可能开展整体性实验(如大型飞机整机,空间站,核电站反应堆等),因而系统整体极小样本或无样本,认知极为匮乏。但在实际工程中,关注的重点恰恰是这些设备或系统整体的可靠性。

在本文中,将这种多层次信息分布不均衡(multi-level & information imbalanced, MLII)系统定义为MLII系统[1-2],图1直观地描述了MLII系统的特性。对于MLII系统的可靠性问题,不能简单理解为传统的“小样本”(系统整体信息匮乏)或一般的“大数据”(底层零部件信息量大)问题,而需针对其信息分布不均衡的特性,提出适用的系统可靠性分析方法。

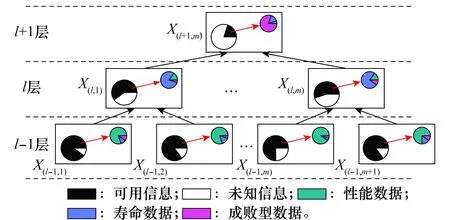
图1 MLII系统图Fig.1 Graphical description of MLII system

1 问题阐述

1.1 MLII系统特性分析

针对MLII系统的特性,一种自然而直观的想法是充分利用系统底层完备的数据集,自下而上地“补偿”顶层匮乏的信息,进而对系统可靠性及其他物理性能参数做出准确的分析与评估。贝叶斯方法作为基于条件概率推断的一种统计方法,将主观信息融入先验分布,以似然函数的形式利用客观数据,综合了所有可用信息后作出概率推理结果,同时针对“小样本”问题同样有效,可作为当顶层信息匮乏时分析系统可靠性的一种手段[3-5],经典贝叶斯推理方法的一般形式为

(1)

但传统的贝叶斯方法在针对MLII系统时存在一些问题。

(1) 在基于贝叶斯理论的统计推断中,先验分布的选取对于后验分布的精度及最终可靠性分析结果的准确性都起到至关重要的作用。在传统的贝叶斯方法中,通常依据专家经验给出适当的参数先验分布,但对于MLII系统而言,系统及子系统层通常信息匮乏,准确的先验分布难以获取,如果仅采用无信息先验分布,在小样本的条件下,难以获得足够精度的可靠性分析结果[5]。对于具有MLII系统特性的复杂机电设备,需对经典的贝叶斯推理算法做出改进,充分利用底层完备数据集的信息,给出具有足够精度的先验分布,以提高分析结果精度。

(2) 复杂机电设备的MLII系统,信息来源广泛,数据多样。即使对于同一事件(例如参数取值),也可能出现相异,甚至完全不同的认知,即所谓的“信息冲突”问题[6]。例如对于相同产品,不同专家根据各自经验给出的故障率、平均故障间隔时间等参数的估测值可能有较大差异,可理解为可能存在的主观信息冲突;又如,对速度、位移等物理量的动力学分析结果可能与通过数理统计获得的估测值存在一定偏差,可理解为可能存在的主客观信息冲突,而经典贝叶斯方法并无处理此类问题的有效机制。

针对经典贝叶斯方法在处理MLII系统可靠性问题时的一些局限性[7-12],提出了基于贝叶斯与信息融合(Bayesian-based information extraction & aggregation, BIEA)的系统可靠性分析与预测方法。

1.2 BIEA方法理论框架

不失一般性,考虑不确定性传递模型Θ=M(θ)中的输入参数向量θ和输出参数向量Θ,分别具有独立的直接先验分布(direct prior,DP)π(θ)和π(Θ)。此时,由于参数向量θ具有独立的先验分布,故参数向量Θ通过关系函数Θ=M(θ)会引入额外的概率分布π*(Θ)。由于信息来源不同,一般情况下,同一参数Θ的先验分布π(Θ)与π*(Θ)不同。

上述问题的实质在于如何综合利用所有可用信息,融合概率分布π(Θ)与π*(Θ)。基于上述考量,定义概率分布融合运算符“⊕”,提出BIEA方法,其基本形式为

(2)

相较于传统的贝叶斯方法,BIEA方法通过构建直接先验分布πD(Θ)与间接先验分布πI(Θ)的方式区分不同来源信息对参数先验分布的影响,定量计算不同信息源对参数先验概率分布的贡献。通过融合先验分布πC(Θ),综合所有可用信息,计算参数后验分布,进而获取所需的可靠性指标,即可靠度、平均故障间隔时间和故障率等。其中直接先验分布πD(Θ)一般基于主观经验获得,而间接先验分布πI(Θ)通过分析模型传递后间接获得。有关该方法与传统贝叶斯方法的异同如图2所示。

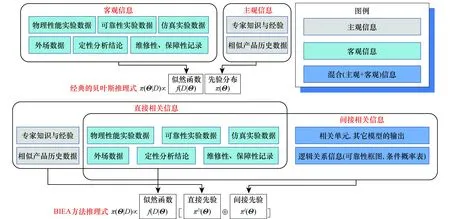
图2 BIEA推理方法融合先验分布构建示意图Fig.2 Sketch map of BIEA reasoning method fusion priori distribution construction

2 基于自更新权重系数的BM概率分布融合方法

2.1 经典BM方法

在BIEA方法中,构建了融合先验分布以替代经典贝叶斯方法中完全由主观经验给出的传统先验分布,即

πC(Θ)=πD(Θ)⊕πI(Θ)

(3)

融合先验分布πC(Θ)由直接先验分布πD(Θ)和间接先验分布πI(Θ)共同构成。其中直接先验分布基于研究对象的直接相关信息,如专家经验,相似产品的历史数据等;间接先验分布则是对研究对象的间接相关信息进行可靠性分析,并利用结构函数间的不确定性传递关系后计算得到。由于信息来源与计算方式均不同,因此同一事件(或参数)的直接先验分布和间接先验分布通常并不一致。一方面,对于研究对象本身是有直观认知的(直接先验分布);另一方面,系统或子系统层的参数与其父节点参数存在函数关系,而MLII系统的似然函数中也包含可靠性函数关系,这都相当于添加了额外的约束,它表明通过结构函数间的不确定性传递关系,上层单元引入了底层信息(额外约束)。而两种不同的概率显然无法直接相互叠加,故需引入一种具有数学一致性与完备性的概率融合方法。

贝叶斯混合(Bayesian melding, BM)是一种经典的概率融合方法,该方法最早由文献[13]提出,可有效地处理2种不同类型的概率分布,在各行各业均有应用[14-15]。融合后的概率分布具有数学完备性,服从概率公理,且能够继承2种不同概率分布的统计特性。经典BM方法通过Pooling的方法构建,常见的线性融合方法为

πC(Θ)∝α·πD(Θ)+(1-α)·πI(Θ)

(4)

对数融合方法为

πC(Θ)∝πD(Θ)απI(Θ)(1-α)

(5)

式中,πC(Θ)、πD(Θ)和πI(Θ)分别为参数Θ的融合先验分布、直接先验分布和间接先验分布；权重系数α∈[0,1]用于平衡直接先验分布和间接先验分布对融合先验分布的贡献量。

2.2 基于自更新权重系数的BM方法

在BM方法中,权重系数α的取值对最终融合先验分布的确定是至关重要的。文献[16]认为这种选取本质上是灵活而非固定唯一的,并讨论了关于权重系数α的取值。在没有额外信息的情况下,同一模型(例如Θ=M(θ))中输入参数(θ)和输出信息(Θ)的可信程度是相同的,文献[16]中例子将α设定为0.5,即直接先验分布和间接先验分布的置信水平是一致的。但事实上,均值0.5的选取方法并不是普遍适用的。文献[17]尝试不同的权重系数α的取值(0.2, 0.4, 0.5, 0.6, 0.8, 0.9),得到了不同的融合先验分布,但发现参数后验分布对α的取值并不敏感,究其原因在于该例子数据充足,样本量较大,使得在推理计算过程中逐渐形成较强的似然函数,足以修正初始先验分布中的偏差。事实上,该例子相较于先验分布,似然函数占据更为主导的位置。而直接先验分布选取无信息先验分布的做法对MLII系统并不适用,如前所述,对于MLII系统中的组件或部件而言,由于实际工况限制,往往数据匮乏,样本量较小,似然函数在计算过程中无法占据主导位置;另一方面,对于底层部件而言,可能包含较多的专家经验等主观信息,因此先验分布的影响不可忽略。在这种情况下,合理选择权重系数α就显得尤为重要。

本论文针对MLII这一类存在信息不均衡特性的系统,提出了一种基于自更新权重系数的BM方法。

对于线性情况,有

πC(Θ)∝πC(Θ|flinear(α,βD,βI))=

(6)

对于对数情况,有

πC(Θ)∝πC(Θ|flog(α,βD,βI))=

(7)

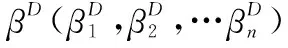
步骤1从参数θ的先验分布πD(Θ)中抽取I个样本(θ1,θ2,…,θI)。从权重系数α的先验分布π(α)中抽取J个样本 (α1,α2,…,αJ)。

步骤2对于抽取的每一个样本θi,通过传递模型Θi=M(θi)计算对应的样本输出值。

步骤3使用非参数估计方法(例如核密度估计)计算间接先验分布πI(Θ)。

步骤4对每一组(θi,αj)的取值计算重要度抽样概率为

步骤5以{wij:i=1,2,…,I;j=1,2,…,J}的概率从 (θi,αj)的离散分布中抽取L个样本,即

π(θ,α)∝{wij:i=1,2,…,I;j=1,2,…,J}

步骤6由于输入参数θ与权重系数α相互独立,因此可以分别计算输入参数θ的离散后验概率分布π(θ|D) 和权重系数α的离散后验概率分布π(α|D)，即

步骤7输出参数Θ的离散后验概率分布π(Θ|D)可通过传递模型Θ(1,2,…,L)=M(θ1,2,…,L)估计,即

本文所提出的基于自更新权重系数的BM方法不预先设定权重系数α的取值,而将其设置为未知超参数,赋予其初始分布,再利用客观数据对其取值修正,实时更新。权重系数α受到似然函数的影响,其取值会在推理过程随着信息的积累而自动变化调整,降低偏离实测数据的先验分布的权重,增加贴近实测数据的先验分布的权重,在反复迭代更新后,权重系数α达到稳定值,此时的后验分布与实测数据吻合度最高。此方法可有效降低先验分布偏差对参数估计结果准确性的影响,提高可靠性分析的精度。而提出的BM方法的另一个优点则是,通过式(5)或式(6)得到融合先验分布是具有解析形式的。考虑到相同概率分布的直接叠加或乘积并不一定服从原始的概率分布形式，即式(3)和式(4)得到的融合先验分布通常并没有解析形式,而这对于多层次的复杂贝叶斯模型,尤其是MLII系统的贝叶斯模型来说很不方便。通过式(5)或式(6)得到的融合先验分布不仅具有明确的解析形式,还可以避免多峰概率分布的出现,这也是在BM方法中经常碰到的问题。

现以简单的例子说明上述问题,分别选择Beta(6,2)和Beta(2,6)作为某参数的直接先验分布和间接先验分布,通过经典BM方法得到的融合先验分布和通过BIEA方法的BM在不同的权重系数α下的融合概率分布如图3所示。

图3 两类BM方法对比Fig.3 Comparisons of the two kinds of BM approaches

可以发现，当权重系数α取极限边界值(0和1)时,2种BM方法所得结果是相同的,这也意味着基于BIEA的BM方法与经典贝叶斯方法具有相同融合边界,即兼容性。但是,对于其他的权重系数α取值(0.2, 0.4,0.6,0.8),经BM方法所得结果呈现出多峰值特征(双峰特性),而BIEA的BM方法仅有一个峰值。在使用BIEA的BM后,参数后验分布为

p(Θ|β)∝L(Θ)πC(Θ|β,α)π(α)

(8)

通过马尔可夫链蒙特卡罗(Markov chain Monto Carlo,MCMC)等抽样方法进行数值计算,此时可反解权重系数α的后验分布，即

p(α)=p(f-1(β))

(9)

通过应用自更新权重系数的BM方法,可以更为精细地平衡基本先验的分布和间接先验分布对融合先验分布的贡献,而融合先验分布也会同时继承2种先验分布的统计特征。该方法为权重系数α的定量量化提供了一种较为灵活的方法。该方法与经典的BM方法有以下不同之处,如表1所示。

表1 经典BM方法与自更新权重系数的BM方法的异同对比

3 MLII系统的BIEA方法

第2节给出了基于自更新权重系数的BM方法的数理算法,下面结合图4所示的多层次结构来阐述MLII系统的BIEA模型。

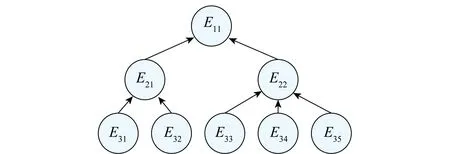
图4 多层次结构系统Fig.4 Multi-level structure system

3.1 MLII系统的BIEA模型

不失一般性,以l行第k个单元E(l,kl)为研究对象,其参数集θ(l,kl)。那么第l+1行的父节点E(l+1,kl+1)则有参数集θ(l+1,kl+1)。给定其参数直接先验分布πD(θ(l+1,kl+1)),其可靠度函数可一般地描述为R(l+1,kl+1)(t)=f(t|θ(l+1,kl+1))。其中，f()是由具体物理背景及失效机理确定的函数。那么,研究对象的可靠度函数及对应的参数概率密度函数的一般形式为

R(l,kl)(t|θ(l,kl))=Ψ(l,kl)(R(l+1,kl+1)(t|θ(l+1,kl+1)):kl+1∈Q(l,kl))

f(l,kl)(t|θ(l,kl))=

(10)

式中,Ψ(l,kl)是由对象单元E(l,kl)及其父节点E(l+1,kl+1)确定的结构函数,Q(l,kl)是所有父节点的指标集。对象单元参数的间接先验分布可通过式(14)的随机变量转换方法来计算，即

(11)

在给定参数直接先验分布πD(θ(l,kl))的基础上,融合先验分布可由式(15)计算，即

πC(θ(l,kl))=πD(θ(l,kl))⊕πI(θ(l,kl))

(12)

融合先验分布中包含了底层数据与信息,并参与当前层次的贝叶斯推理过程,重复这一过程,就可以将底层完备的信息逐渐传递至顶层,在系统级综合所有可用信息,做出较为准确的可靠性分析。

依据贝叶斯理论,在给定参数先验分布与似然函数的情况下,MLII系统的BIEA模型由(16)给出，即

π(Θ|D)∝πC(Θ)×L(D|Θ)=

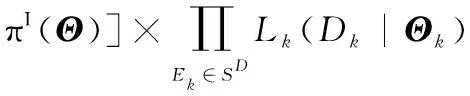
(13)

式中,融合先验分布πC(Θ)考虑了直接先验分布πD(Θ)和间接先验分布πI(Θ)的2部分贡献;联合似然函数由所有包含可用信息的父节点似然函数构成,π(Θ|D)是考虑信息融合后模型参数集的后验分布。一般情况下,式(13)不存在解析解。通过使用各类MCMC方法,如Metropolis-Hastings方法(文献[18])或Gibbs 抽样方法(文献[19])可获得数值解。在本论文中,使用OpenBUGS(一种基于Gibbs抽样做贝叶斯分析的开源软件包)进行计算,详细内容可参考[20]。

3.2 可靠性指标计算

通过式(16)可获得所关心参数的联合后验分布π(Θ|D),但在可靠性工程中,可能更关系某些特定的可靠性指标，如可靠度、故障率等。

可靠度为

(14)

故障率为

(15)

平均故障时间(mean time to failure,MTTF)为

(16)

式中,D是MLII系统的可用数据集；R(tp|D)和λ(tp|D)分别是在tp时刻的可靠度与故障率。

现将BIEA方法的主要步骤罗列如下,其主要分析流程及与经典贝叶斯方法的异同如图5所示。

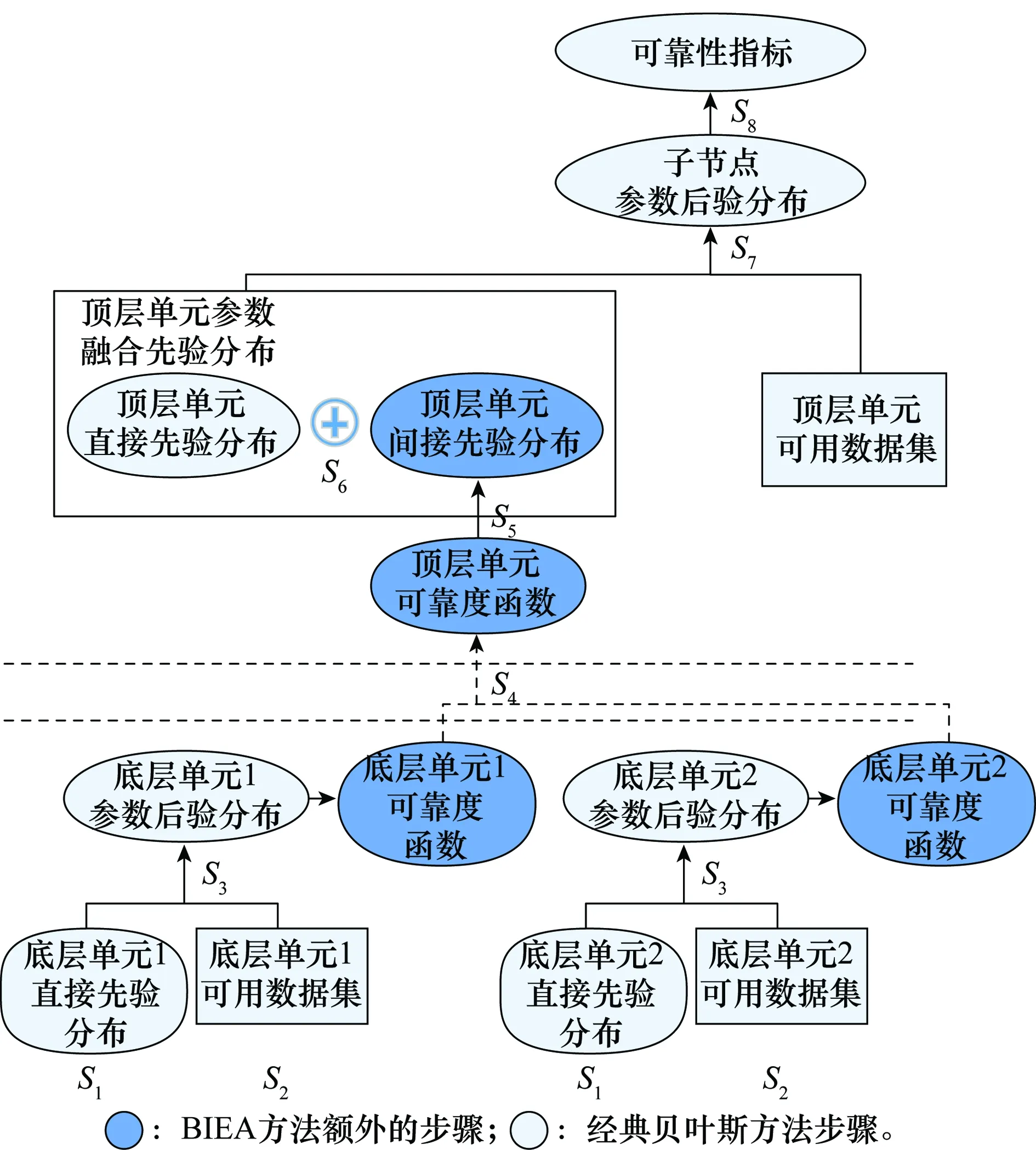
图5 BIEA系统可靠性分析方法流程图Fig.5 Flow chart of BIEA system reliability analysis method

步骤1依据各单元结构特性,选取适当的描述模型,给出参数直接先验分布;

步骤2基于可用数据集建立似然函数;

步骤3应用贝叶斯更新计算参数后验分布;

步骤4基于系统结构组成,计算系统可靠度函数表达式;

步骤5利用随机变量转换关系,获得参数间接先验分布;

步骤6应用BM算法计算参数融合先验分布;

步骤7基于融合先验分布计算更新后的参数后验分布;

步骤8模型输出各类可靠性指标。

4 方法验证与案例分析

4.1 模型描述

为了验证所提出的BIEA方法对MLII系统可靠性分析的有效性,选择文献[17]中的经典双层串联系统,其模型结构与参数设置具有MLII系统的特性,如图6所示。

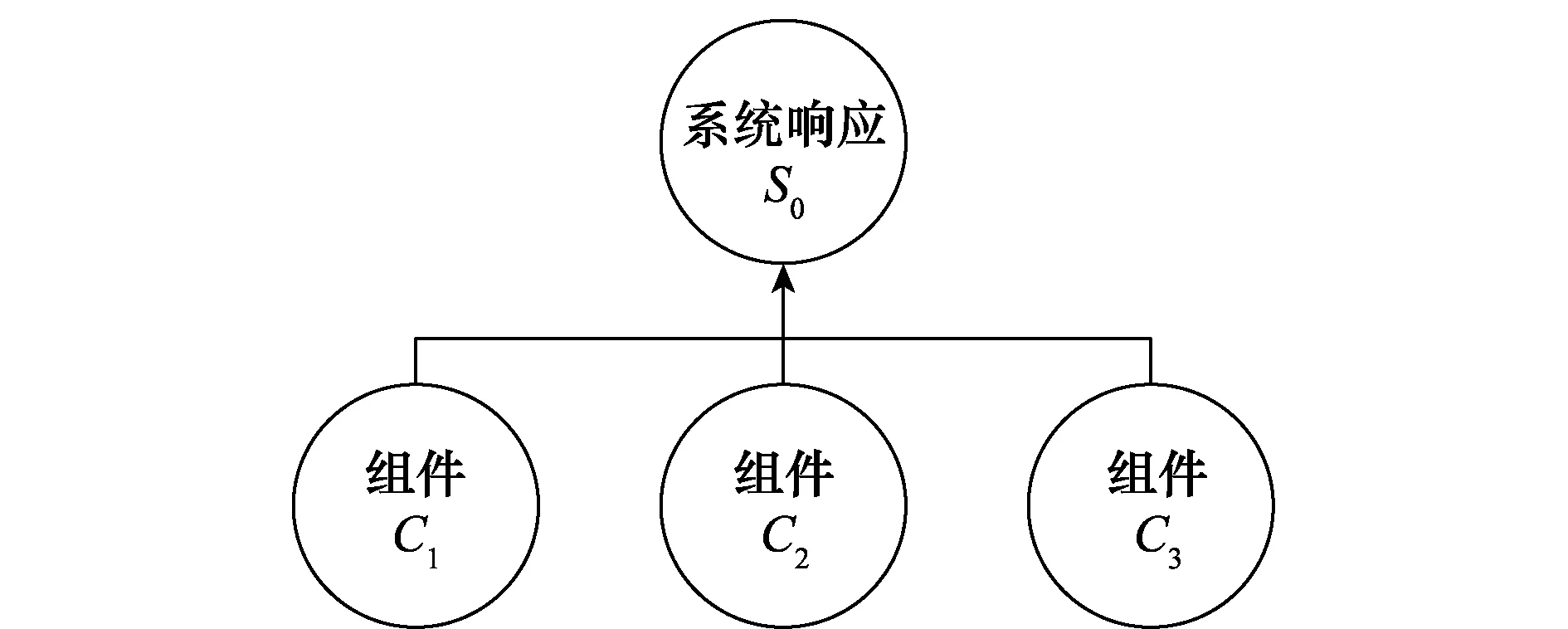
图6 双层次结构模型Fig.6 Two level structure model

具体地，C1、C2和C3分别为3类具有不同可靠性模型的组件。对于C1,其可靠性模型为logistic回归模型,可用数据包含25个测试单元在11个时间点的二项型成败记录;对于C2,其可靠性模型服从双参数的威布尔分布,可用数据包含25个测试单元的失效时间数据;对于C3,选取的是性能退化模型,可用数据包含研究对象在10个时间点的性能退化数据。相关数据参如表2所示。为了保证对比的有效性,相关可靠性模型与模型参数的设置都与文献[17]中例子一致。C1、C2和C3的可靠度函数分别由式(17)～式(19)给出。

R1(t|Θ1)=logit-1(θ1+η1t),Θ1=(θ1,η1)

(17)

(18)

(19)

基于表2中的有效数据集,可分别确定C1、C2和C3的似然函数,而未知参数的后验分布可通过基于MCMC的抽样方法计算得到。C1:成败型数据(25样本/时间点),C2:寿命数据(样本量25),C3:退化数据(1样本/单元/时间点)。本文使用OpenBUGS软件分别计算C1、C2和C3的可靠度随时间变化曲线，结果如图7所示,Mean为均值,Val 2.5%为置信度2.5%分位值,Val 97.5%为置信度97.5%分位值。

表2 C1、C2和C3的可用数据

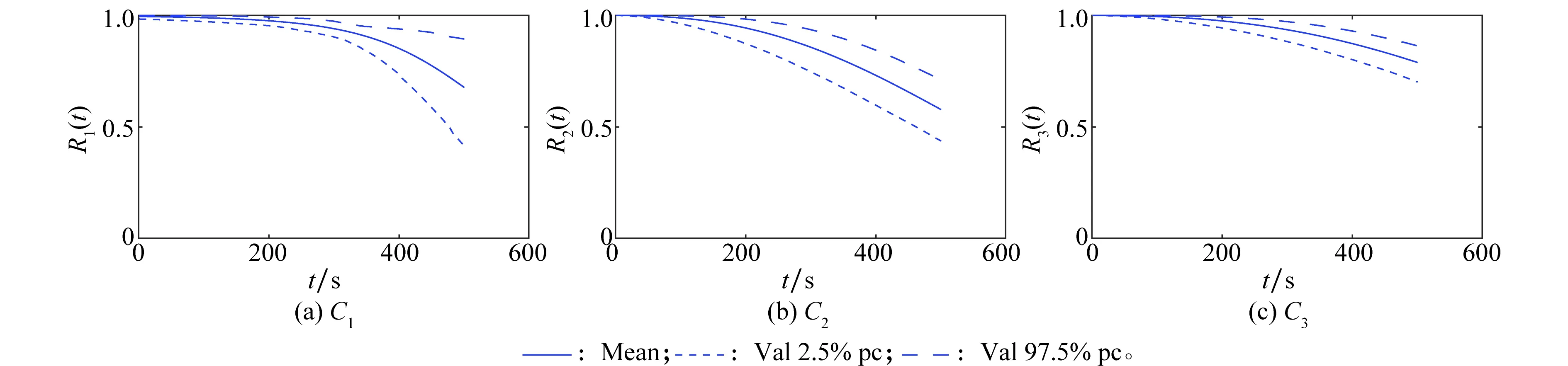
图7 C1、C2和C3的可靠度随时间变化曲线Fig.7 Time variation curves of reliability for C1、C2 and C3

根据串联系统结构函数,可得系统的可靠度函数为

R0(t|Θ0)=R1(t|Θ1)R2(t|Θ2)R3(t|Θ3)=

(20)

为了验证所提出的BIEA方法在信息分布不均衡情况下的有效性,分别对系统层参数的先验分布与可用数据考虑以下3类不同的情况:①先验分布为平坦的无信息先验分布且具有充足数据集(样本量50);②相同的无信息先验分布,但仅为小样本,稀疏数据集(样本量10);③先验分布为非平坦的偏态分布,以此来模拟具有较强主观意向的专家经验,同时样本量保持为10的小样本。为消除参数相关性的影响,假设系统的故障时间服从指数分布,故其可靠性模型仅包含唯一的参数λ。

对于每一种情况,都分别应用简单贝叶斯方法(无BM),经典BM方法和BIEA方法进行参数估计与可靠性分析,并将结果做对比。需要注意的是,由于简单贝叶斯方法不区分直接先验分布和间接先验分布,故在进行系统层的可靠性分析时,是不包含底层信息的,而2种BM方法则包含所有信息。为了唯一确定系统可靠性预测曲线,假设系统的可靠度函数R0(t|λ)在某特定时间(t=20)服从Beta分布((beta(1,1) 或 beta(15,70)),那么根据λ和R之间的函数关系,可以得到关于参数λ的间接先验分布。这样,融合先验分布就同时包含了直接先验分布和间接先验分布。系统层的数据是基于λ真值0.012抽取的仿真数据。3种情况中所涉及的先验分布与可用数据如表3所示。

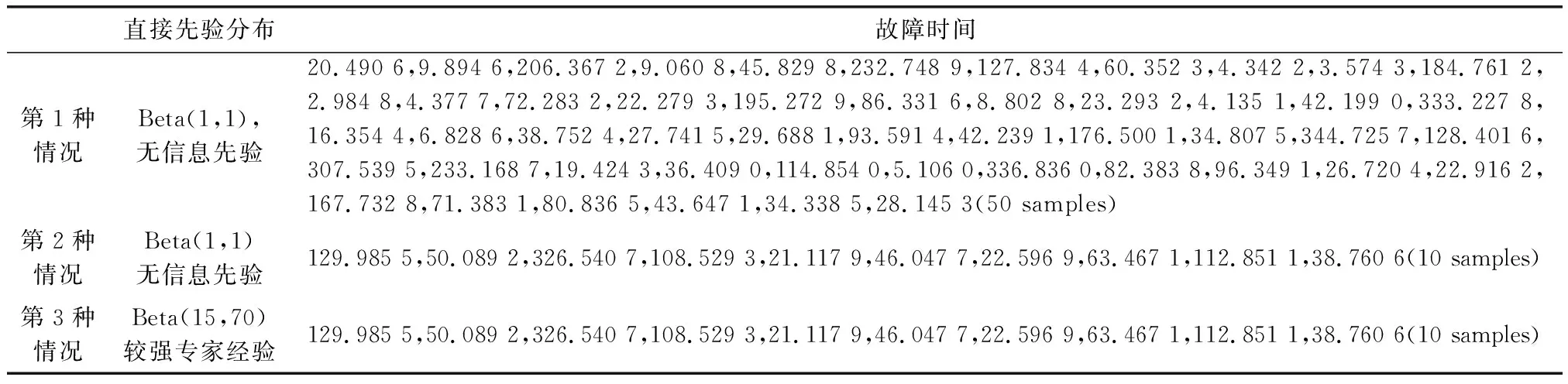
表3 3种情况下系统层的可用数据

使用式(6)的形式构建融合先验分布,由于直接先验分布πD(λ)和间接先验分布πI(λ)均服从beta分布,因此对于经典BM方法和基于BIEA的BM方法,融合先验分布πC(λ)分别有

πC(λ)∝πD(λ)απI(λ)(1-α)

(21)

Beta((aD)α(aD)1-α,(bD)α(bD)1-α)

(22)

式中,a和b为beta分布参数。对于经典BM方法,分别选择不同的权重系数(α=0.2,0.4,0.6,0.8),混合后的融合先验分布如图8所示。

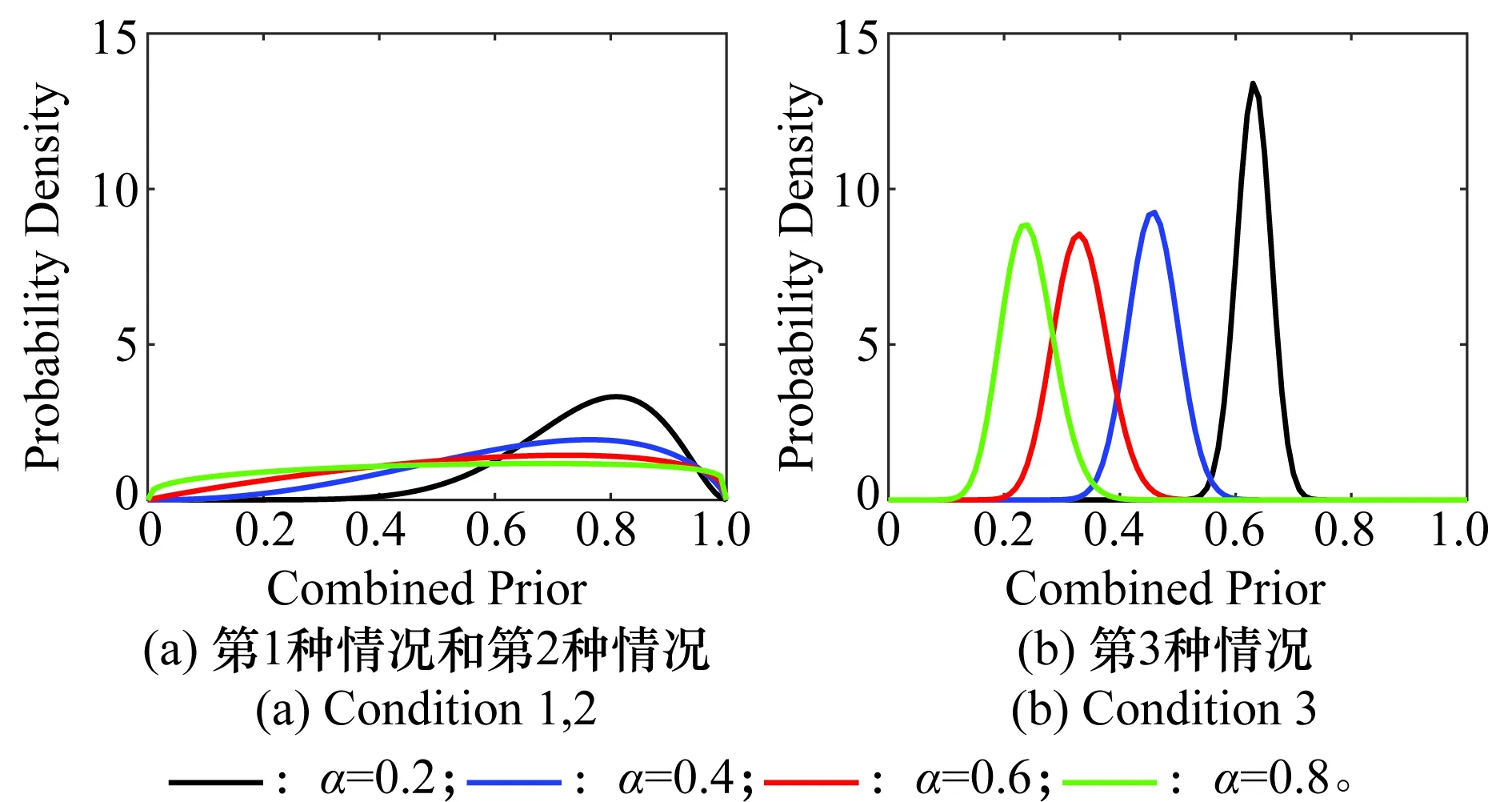
图8 不同权重因子(α=0.2,0.4,0.6,0.8)对应的融合先验分布Fig.8 Combined prior of different weighing factor (α=0.2,0.4,0.6,0.8)

4.2 分析与讨论

表4～表6分别给出了3种不同情况下,分别应用简单贝叶斯方法、经典BM,基于自更新权重系数的BIEA方法3种方法的参数估计结果;图9给出了3种情况下,应用3种不同方法所得的可靠性预测曲线对比结果,CB为简单贝叶斯,TM为经典BM,AM为自更新BM。参数估计结果是利用OpenBUGS软件中的统计工具箱计算完成后,在Matlab中绘图得到的。

图9 3种情况下不同方法的系统可靠性预测结果Fig.9 Prediction results of system reliability of different methodsunder three conditions

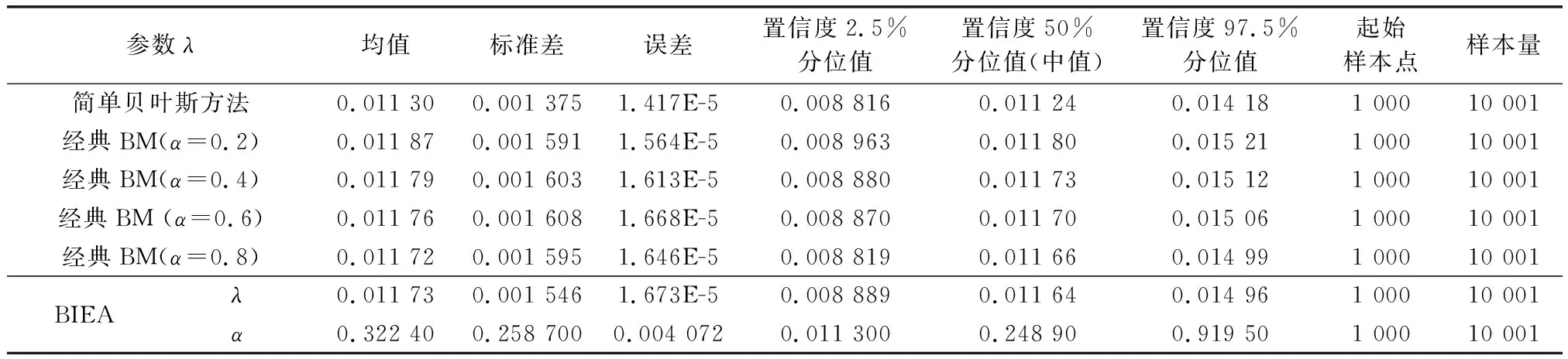
参数λ均值标准差误差置信度2.5%分位值置信度50%分位值(中值)置信度97.5%分位值起始样本点样本量简单贝叶斯方法0.011 300.001 3751.417E-50.008 8160.011 240.014 181 00010 001经典BM(α=0.2)0.011 870.001 5911.564E-50.008 9630.011 800.015 211 00010 001经典BM(α=0.4)0.011 790.001 6031.613E-50.008 8800.011 730.015 121 00010 001经典BM (α=0.6)0.011 760.001 6081.668E-50.008 8700.011 700.015 061 00010 001经典BM(α=0.8)0.011 720.001 5951.646E-50.008 8190.011 660.014 991 00010 001BIEAλ0.011 730.001 5461.673E-50.008 8890.011 640.014 961 00010 001α0.322 400.258 7000.004 0720.011 3000.248 900.919 501 00010 001

表5 第2种情况下的参数统计结果

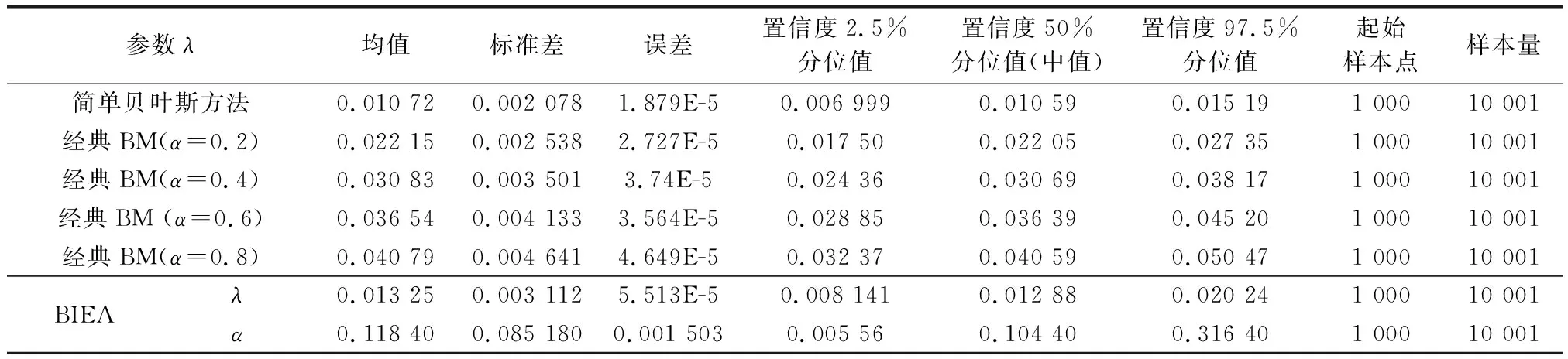
表6 第3种情况下的参数统计结果

由图9可见,在理想情况下(无偏先验分布&充足样本)3种方法都可以得到令人满意的结果(见图9(a))。参数估计的结果对不同权重系数α的取值并不敏感(见表4)。此时,3种方法得到的可靠性预测曲线几乎是一致的,这一现象也与文献[17]的描述相符。

当样本量逐渐减小后(从50减至10),应用BM方法(经典贝叶斯或BIEA)的分析与预测结果,其准确性超过简单贝叶斯方法的结果(见图9(b))。这说明对于存在小样本问题的非理想情况,应用BM可以改善分析精度,提高预测的准确性。在第2种情况中,使用经典BM方法时,当权重系数从0.2变化至0.8的过程中,参数估计的结果发生了变化(见表5),这是由于样本量从50减至10后,似然函数的主导性显著降低所致。

当存在较强的专家经验而可用数据又匮乏时，即信息非均衡的MLII系统,使用经典的BM方法也难以保证分析的准确性(见图9(c)的蓝色曲线)。而对于基于BIEA的BM方法,即使先验分布中存在主观偏差(beta(15,70)),其分析与预测结果仍然具有较高的精度(90%置信区间)。

事实上,在非理想情况下(偏差先验分布,小样本有限数据),有限的数据集不足以构建占据主导地位的似然函数,故而先验分布对最终结果的影响较大。此时,参数估计的结果对权重系数α的取值较为敏感,权重系数α须有较高精度。方法通过将权重系数α设为不确定性参数,可以利用数据在推理过程中不断更新α的取值,进而自动地平衡直接先验分布和间接先验分布对融合先验分布的影响。

经典的BM方法将权重系数α设定为确定值,这对一般系统而言是可以接受的。但这对似然函数无法占据主导位置的MLII系统是不适用的。基于BIEA的BM方法通过将权重系数设为超参数的方法,在推理过程中使其与其他参数一起更新,通过这种方式,底层信息也参与到系统顶层对象的可靠性分析过程中。基于BIEA的BM方法在系统层面上重新求解了信息不均衡问题,即使先验分布存在偏差,样本量较小,参数估计结果的精度仍是可接受的。

5 结 论

本文就传统可靠性分析与预测方法在处理含有MLII系统时的一些局限性,提出了基于BIEA的系统可靠性分析与预测方法。该方法主要针对在实际工程中存在的MLII系统的2类特点——多层次与信息分布不均衡，对经典贝叶斯推理方法作出改进,使之可充分利用底层单元的完备数据,自下而上地补偿顶层匮乏的信息,获得较为准确的系统可靠性分析与预测结果。该方法可广泛应用于具有MLII系统特性的复杂机电设备的可靠性工程,降低分析结果的不确定性,提高预测精度。

参考文献：

[1] LI M, LIU J, LI J, et al. Bayesian modeling of multi-state hierarchical systems with multi-level information aggregation[J]. Reliability Engineering & System Safety,2014,124(124):158-164.

[2] YANG L, ZHANG J, GUO Y, et al. Bayesian-based information extraction and aggregation approach for multilevel systems with multi-source data[J]. Journal of Systems Engineering and Electronics, 2017, 28(2): 385-400.

[3] RUI K, ZHANG Q, ZENG Z, et al. Measuring reliability under epistemic uncertainty: review on non-probabilistic reliability metrics[J]. Chinese Journal of Aeronautics,2016,29(3):571-579.

[4] PAN R, YONTAY P. Discussion of “Bayesian reliability: combining information”[J]. Quality Engineering,2017,29(1): 136-140.

[5] HAMADA M S, WILSON A G, REESE C S, et al. Bayesian Reliability[M]. New York: Springer, 2008.

[6] WILSON A G, FRONCZYK K M. Bayesian reliability: combining information[J]. Quality Engineering,2016,29(1):119-129.

[7] LI M, HU Q, LIU J. Proportional hazard modeling for hierarchical systems with multi-level information aggregation[J]. IIE Transactions, 2014, 46(2): 149-163.

[8] HAMADA M, MARTZ H F, REESE C S, et al. A fully Bayesian approach for combining multilevel failure information in fault tree quantification and optimal follow-on resource allocation[J]. Reliability Engineering & System Safety,2004,86(3):297-305.

[9] WILSON A G, REESE C S. Advances in data combination, analysis and collection for system reliability assessment[J]. Statistical Science, 2007, 21(4): 514-531.

[10] WOODS D C, OVERSTALL A M, ADAMOU M, et al. Bayesian design of experiments for generalized linear models and dimensional analysis with industrial and scientific application[J]. Quality Engineering, 2016, 29(1): 91-103.

[11] REESE C S, WILSON A G, GUO J, et al. A Bayesian model for integrating multiple sources of lifetime information in system-reliability assessments[J]. Journal of Quality Technology, 2011, 9(4): 489-495.

[12] YONTAY P, PAN R. A computational Bayesian approach to dependency assessment in system reliability[J]. Reliability Engineering & System Safety, 2016, 152: 104-114.

[13] POOLE D, RAFTERY A. Inference for deterministic simulation models: the Bayesian melding approach[J]. Publications of the American Statistical Association,2000,95(452):1244-1255.

[14] LIU Y, ZIDEK J V, TRITES A W, et al. Bayesian data fusion approaches to predicting spatial tracks: application to marine mammals[J].Annals of Applied Statistics,2016,10(3):1517-1546.

[15] LI Z S, GUO J, XIAO N C, et al. Multiple priors integration for reliability estimation using the Bayesian melding method[C]∥Proc.of the IEEE Reliability and Maintainability Symposium, 2017.

[16] FRENCH S. Group consensus probability distributions: a critical survey[J]. Bayesian Statistics, 1985, 2: 183-201.

[17] GUO J Q, WILSON A G. Bayesian methods for estimating system reliability using heterogeneous multilevel information[J]. Technometrics, 2013, 55(4): 461-472.

[18] GELFAND A E. Sampling-based approaches to calculating marginal densities[J]. Publications of the American Statistical Association, 1990, 85(410): 398-409.

[19] SMITH A F M, ROBERTS G O. Bayesian computation via the Gibbs sampler and related Markov chain Monte Carlo methods[J]. Journal of the Royal Statistical Society, 1993, 55(1): 3-23.

[20] KRUSCHKE J K. Doing Bayesian data analysis: a tutorial with R and BUGS[J]. Cognitivesciencesociety Org,2013,1(5):737-745.