基于电动汽车充电导航的快充负荷有序接入研究

宋汶秦， 靳攀润， 孙亚璐， 徐慧慧， 苏 舒

(1. 国网甘肃省电力公司经济技术研究院， 甘肃 兰州 730050；2. 强电磁工程与新技术国家重点实验室， 华中科技大学， 湖北 武汉 430074)

1 引言

电动汽车的推广和普及有助于缓解化石能源危机，减轻环境污染[1-3]。随着电动汽车渗透率的逐步提高，用户的充电需求也将不断增大。快速充电作为一种重要的充电方式能够在短时间内满足用户急迫的充电需求，是未来充电技术发展的重要方向。对于电动汽车用户而言，充电导航功能能够极大地提升其充电体验，完善的充电导航系统应兼顾交通状况和电网潮流状态，考虑用户的充电时间和充电成本，为用户制定人性化的充电方案[4,5]。电动汽车作为交通工具和电力负荷将同时作用于交通系统和电力系统，为了弱化电动汽车充电所带来的不利影响，需要对电动汽车用户的充电行为进行引导，从而实现有序充电[6-8]。

对于集群化的电动汽车的充电负荷分析，现有的充电负荷确定方法主要包括基于出行需求的分析法[9,10]和基于充电站的充电负荷分析法[11]。文献[12]将家用车辆出行目的分为五大类，构建简单和复杂出行链，提出了基于电动汽车行驶出行链的考虑充电频率的电动汽车充电负荷预测方法。文献[13]提出了考虑电动汽车多日一充模式时的负荷建模方法，该方法能够提高充电负荷特性分析的准确性。文献[14]借鉴汽车加油统计规律建立了单台电动汽车功率需求的统计模型，并借助统计学原理分析了多台电动汽车同时充电的最大负荷功率。文献[15]通过分析充电站的进站车辆流量对充电负荷的影响，提出了描述充电站负荷的数学模型和动态仿真方法。

在有序充电控制策略方面，文献[16]总结了充电调度控制的效益，并综述了充电控制策略领域的一些研究成果。目前的相关研究中，有序充电的控制目标主要包括减小峰谷差、减少网损、抑制电压偏移等，文献[17]介绍了以削峰填谷、有功调频调峰、电压无功控制等作为控制功能的充电控制策略。文献[18]提出了一种配电变压器层面上的vTOU-DP策略，在减小峰谷差方面效果明显；文献[19]提出了一种以等效负荷曲线方差最小为目标的有序充电调度策略，有效提高了负荷率；文献[20]提出了一种基于配电系统网损最小的有序充电控制策略；文献[21]从安全性和经济性两方面出发，同时以最小化配电网功率损耗和减小电网等效负荷峰谷差为目标，建立了各个节点上电动汽车的最优充电调度策略。

在考虑电网侧的充电导航系统方面，文献[22]提出了基于实时电价的智能充电导航系统，该系统能够为用户提供时间最优、成本最优、综合最优三种充电策略，通过该系统能够有效降低用户的充电成本，同时改善配电系统电压水平；文献[23]提出了一种考虑实时交通状况和电网运行状态的快速充电导航策略，计及行驶时间、等待时间和充电时间，基于用户充电总时间最短的原则，为用户提供充电位置导航，仿真结果显示，该策略能够减少用户的充电总时间。

综上所述，现有的相关研究在不同场景下的有序充电引导控制手段方面已经获得了丰富的研究成果，这为本文的相关研究打下了坚实的理论基础。但是，目前有序充电控制策略研究的控制对象主要是慢充用户，研究中涉及的优化策略大多是基于集群效应，没有具体到每一台电动汽车的充电行为，而且也鲜有空间尺度上的有序充电控制的相关研究。所以，这些研究基础并不能直接套用到快充用户的有序充电策略当中。

为此，本文首先提出了电动汽车充电导航系统架构，该系统综合了用户侧、电网侧和交通侧三个方面。对于用户侧，本文对电动汽车用户的充电位置选择标准进行了分类，对于不同类型的用户，在进行充电位置的选择时应当考虑距离、时间、成本等不同的属性；对于电网侧，本文分析了快充站所在节点的配电系统电压可承受度，该指标将影响充电站内充电桩的充电功率，并将进一步影响用户的充电时间；对于交通侧，本文分析了充电导航过程中的最优路径规划方法，结合交通侧和电网侧提供的信息，用户能够借助充电导航系统车载终端按照不同的选择标准进行充电导航。最后，通过基于IEEE33节点配电系统的仿真算例，对比分析I类用户和II类用户的充电导航结果，说明了本文所提出的基于电动汽车充电导航的快充负荷有序接入策略的有效性。

2 电动汽车充电导航系统

目前已经广泛应用的车辆导航系统只考虑交通状况，在车主设定目的地后，为其提供最短方案或最快方案。随着未来电动汽车的普及，快速充电的需求将不断增长，在大规模无序快充负荷接入的场景下，现有的车辆导航系统不仅不能缓解电网的负荷接入压力，而且不能为用户提供更优质的导航结果。因此，针对电动汽车的充电导航系统应该考虑电网的运行状态。完整的电动汽车充电导航系统如图1所示。该系统包含三个部分：

(1)用户部分，包括EV车主和充电导航系统车载终端。

(2)电网部分，包括配电管理系统(Distribution Management System, DMS)和快充站。

(3)交通部分，包括智能交通系统(Intelligent Transportation Systems, ITS)。

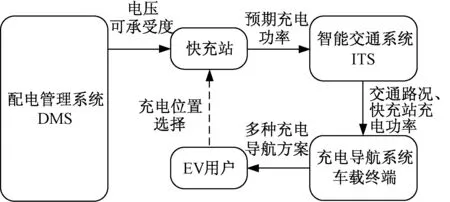
图1 电动汽车充电导航系统的构成及数据流Fig.1 Architecture of smart charging navigation

随着ITS的发展，用户能够获取更丰富的交通信息，在ITS和DMS的基础上，构建电动汽车充电导航系统，能够为用户提供更为人性化的充电体验。通过充电导航系统车载终端，用户能够结合ITS提供的交通路况、DMS和快充站提供的预期充电功率，考虑自身的充电需求，进行充电方案选择和充电路径导航。

结合充电导航系统的数据流，用户采用“预约式充电+消费一体化”服务，完整过程如下：首先，由DMS根据配电系统当前的负荷水平向快充站发布其所在节点的可接入负荷容量(本文将其定义为可承受度)；快充站以避免用户排队等待为原则，充分利用已有的充电桩，在可承受度的基础上为各个充电桩分配充电功率，并向ITS发布其预期充电功率；ITS整合快充站的功率信息和交通信息，发布至充电导航系统车载终端；EV用户借助充电导航系统车载终端，获取可行的充电导航方案，并从中挑选符合自身需求的最佳方案。

综上所述，EV充电导航策略的关键问题包括以下三个方面：

(1)从用户部分考虑，为了满足用户的多样化充电需求，应充分分析用户的充电位置选择倾向，从而为不同类型的用户提供人性化的充电导航方案。

(2)从电网部分考虑，为了弱化规模化快充对配电系统产生的不利影响，应对配电系统的不同节点在不同时间内可接入负荷的能力进行分析，并研究考虑配电系统可接入负荷容量的充电站内充电桩的充电功率调节方法。

(3)从交通部分考虑，应研究合适的最优路径规划方法，为用户提供不同属性下最佳的充电导航路径。

本文将对上述三方面的问题展开分析。

3 基于电动汽车充电导航的快充负荷有序接入引导方法

3.1 电动汽车快充用户充电位置选择标准分类

对于不同的EV用户而言，其充电行为不尽相同。对EV用户的行为分析主要包括用户的充电开始时间选择分析、充电位置选择分析两方面。由于快充用户的特殊性，在不考虑排队等待时，用户会在到达快充站的第一时间进行充电，以解决急迫的快充需求，因此，充电时间是刚性的，充电开始时间一般不能改变。本节主要对用户充电位置的选择标准进行分析。

假设用户都是理性的，电动汽车用户在产生快充需求之后，在车辆剩余荷电状态(SOC)可达的前提下，其对充电站的选择倾向大致可以分为以下几类：

(1)I类用户，在不能接入ITS的前提下，不能获取实时路况，选择最近的快充站。

(2)II类用户，在能够接入ITS的前提下，选择最快完成充电过程的充电站。

(3)III类用户，在能够接入ITS的前提下，同时考虑充电总时间和充电总成本，综合判断来选择充电站。

充电总时间的构成如式(1)所示：

Td=Ta+Tq+Tc+Te

(1)

式中，Td为充电总时间(h)；Ta为到站时间，即行驶到充电站所耗费的时间(h)；Tq为排队时间(h)；Tc为充电时间，即从开始充电到充电完毕所耗费的时间(h)；Te为离站时间，即从充电站行驶到目的地所耗费的时间(h)。

充电总成本的构成如式(2)所示：

Cd=Ca+Cs+Ce=Ct+Cc+Cs+Ce

(2)

式中，Cd为充电总成本(元)；Ca为到站充电成本(元)，即考虑车辆行驶过程中的电量消耗，在车辆到达相应充电站后充电时的充电成本；Cs为充电服务费成本(元)；Ct为行驶成本(元)，即车辆在行驶到相应充电站的过程中消耗的电量对应的充电成本；Cc为即刻充电成本(元)，即车辆在产生快充需求时立即充电时的充电成本；Ce为离站充电成本(元)，即考虑车辆从充电站行驶到目的地的电量消耗，在车辆离开相应充电站后消耗的电量对应的充电成本。

本文主要对I类用户和II类用户进行分析。

3.2 基于配电网可承受度的快充站预期充电功率

连续潮流法(Continuation Power Flow, CPF)是电压稳定性分析的常用手段[24,25]，通过该方法绘制PV曲线可以得到负荷功率极限Pm。但是，该功率极限往往用于分析系统的电压稳定裕度，系统在正常的运行状态下距离PV曲线的临界点非常远，该功率极限Pm不能反映快充站有可能存在的负荷接入情况。另一方面，配电系统的正常运行需要满足电能质量的约束，通过PV曲线可以得到与电压幅值限值(电能质量约束)相对应的负荷功率值，该负荷功率值相比功率极限Pm要更加严格，且更能反映快充站可能存在的负荷接入的实际情况。因此，将由配电系统的电能质量约束所限定的快充接入功率上限Pssm作为快充站所在节点的配电系统电压可承受度D，即

D=Pssm=λb

(3)

式中，λ为功率变化参数；b为功率变化向量。可承受度D反映的是快充站所在节点在当前配电网的负荷条件下对快充负荷的接纳能力。

快充站内的充电桩位是固定的，当快充站的快充需求较多时，本着充分利用充电设施且尽量避免用户等待的原则，应尽可能地满足EV用户的快充需求，将尽可能多的待充电车辆接入可用的充电桩。如果本时段内该站所在节点的配电系统电压可承受度较低，那么充电桩不能为用户提供满功率充电，而应降低充电功率，避免配电网受到影响。

按充电功率平均分配的原则，每个快充桩分配的充电功率如式(4)所示：

从表3我们可以看出，在词性、词意和搭配错误方面显著性水平为.000，说明词汇是区分高低分作文的显著性因素；在篇章结构和文章主题方面的显著性水平达到了.021和.025,在语法和句式方面的显著性水平为.032，拼写方面的显著性水平也达到了.045，均低于0.05，说明在区分高低分作文时，这些因素发挥着重要的作用。此外，我们注意到，篇章结构的错误数量虽然不多，但教师在批改时却作为一个重要的评价标准。

(4)

式中，n为正在充电的快充桩的数量；Pmax为快充桩所能提供的最大快充功率。

根据图1所示的充电导航系统，快充站需要向ITS反馈预期的充电功率。由于实际的充电功率需要考虑到电动汽车的接入数量，是一个难以预计的值，因此，快充站可以将本时段内的最小充电功率(即所有充电桩都接入负荷时的充电功率)和最大充电功率上传至ITS，进而为用户的充电导航方案提供参考。

3.3 电动汽车充电最优路径规划

电动汽车充电导航功能包括充电位置的确定和充电路径的规划。充电导航系统车载终端能够采用路径最短或通行时间最短的原则为用户规划从当前位置到附近充电站的最合适路径，用户通过比对到达各个充电站的最合适路径的属性值(距离、时间、成本)，选择最佳的充电位置，充电导航系统车载终端进一步为用户形成充电导航方案。用户的充电位置选择标准如式(5)所示：

Xs=min{X1,X2,…,Xn}

(5)

式中，Xs为用户最终选择的充电位置所对应的属性值；X1～Xn分别为到达附近n个快充站的最合适路径的属性值。

用户所考虑的属性与自身的选择标准有关，在属性确定后，充电导航问题可以简化为最优路径规划问题。最优路径是交通网络路径分析的核心内容，它不仅包括距离层面的最短路径，还包括时间、费用等属性最优的路径，因此，最优路径也可以看作广义的最短路径。

城市交通网络可以用有向带权图进行建模，进而借助图论的相关理论进行分析。采用有向带权图建模后，网络图中的节点代表城市交通网络中的交叉路口，网络图中的带权弧代表交叉路口之间的城市道路路段，城市道路网络模型如式(6)所示：

G={V,E}

(6)

式中，G为路网模型；V为顶点(路段交叉口)集合；E为所有带权弧的长度(道路路段距离)集合。E中可以包含更为丰富的道路属性，除了路段起止节点和路段长度外，还可以包含路段等级、拥挤程度等。

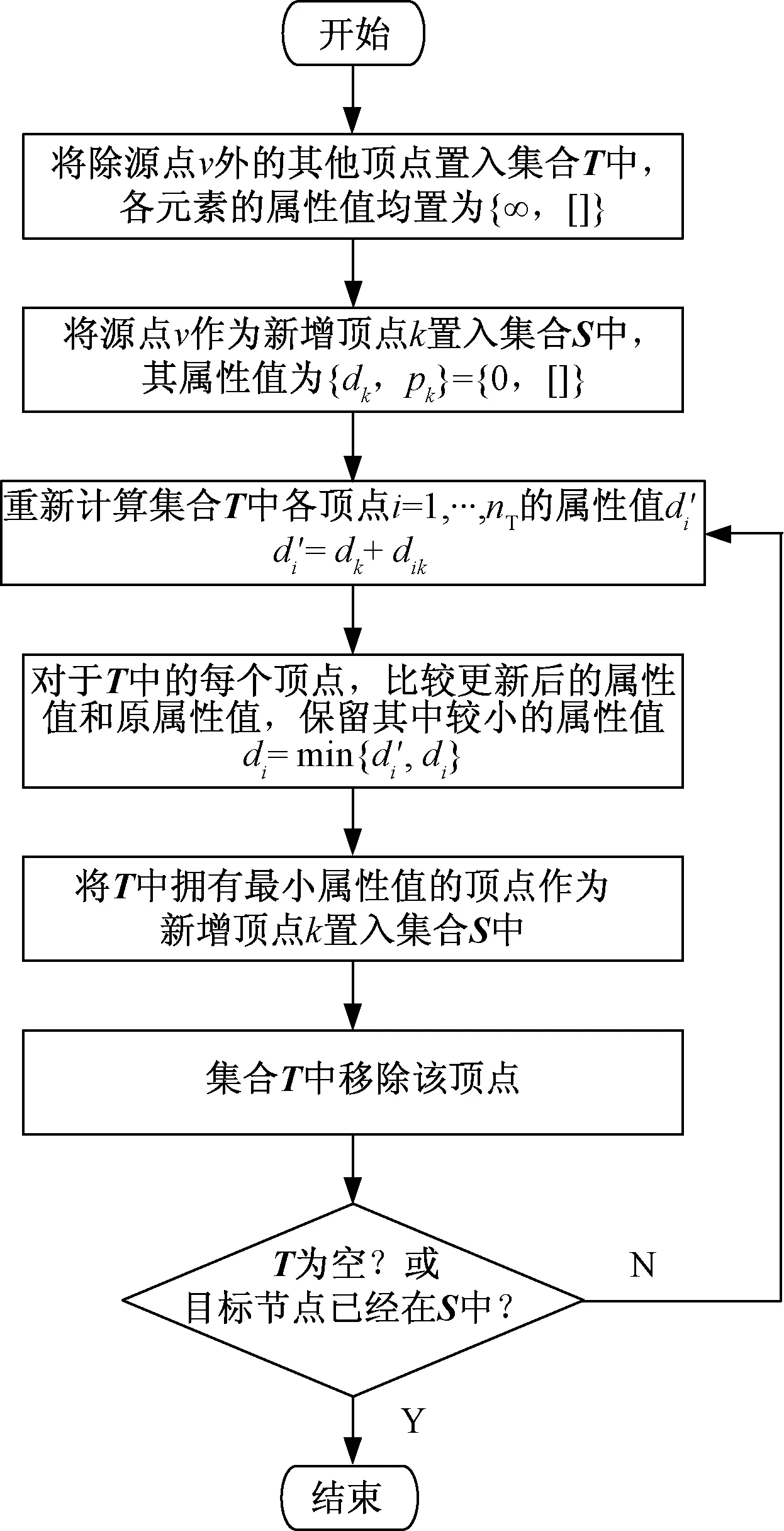
图2 Dijkstra算法计算流程Fig.2 Flow chart of Dijkstra algorithm

目前，已经有多种成熟的方法可以解决最优路径问题，其中，最具代表性的是Dijkstras算法。Dijkstra算法是一种宽度优先搜索算法，其计算流程如图2所示。图2中，dik为顶点i和k的直接距离，若顶点之间无直连弧，则取为∞。在图2所示的Dijkstra算法的基础上，可以得到从源点出发到各个顶点的最优路径。

电动汽车快充路径规划的过程是求取从产生快充需求的位置到附近充电站的最优路径的过程，由于电动汽车用户一般在道路路段上产生快充需求，在网络建模时，如果以用户产生快充需求时所在的位置作为源点，则需要在原来的道路交通网络形成的有向带权图的基础上新增一个顶点，这样需要修改原图的基础数据，形成新的有向带权图G′。当用户在不同路段、不同位置产生充电需求时，将导致针对不同用户的有向带权图G′不能共用，因而不适用于含大量快充负荷充电需求场景下的分析计算。

在城市交通网络建模的过程中，通过对有向带权图的弧赋予不同属性的权值，结合最优路径算法，可以得到考虑不同属性的最优路径。将路段距离作为弧属性，可以得到最短路径，满足I类用户的需求；将路段行驶时间作为弧属性，可以得到最快路径，满足II类用户的需求。

对于II类用户而言，充电导航系统车载终端通过最优路径规划可以获得最短的到站时间，此外，充电导航系统车载终端还需要结合快充站发布的预期充电功率计算充电总时间。由式(1)，在不考虑排队的情况下，预期的充电总时间为：

(7)

式中，Cap为车辆电池容量；SOCa为车辆的到站荷电状态；Pex为预期充电功率，可以取为快充站发布的最大充电功率Pmax和最小充电功率Pmin的平均值：

(8)

修正后的预期的充电总时间可以提供给用户作为充电导航方案的选择依据。

4 算例仿真

4.1 仿真参数设置

算例分析的区域如图3所示，IEEE 33节点配电系统如图4所示。图3中给出了该区域的主干道路交通网络，该区域的两座快充站分别位于A、B两点，进站方向见图3，其中A站与交叉路口11的距离为220m，B站与交叉路口25的距离为380m。所有路段均为双向车道，车辆只能在交叉路口处掉头。快充站A位于图4所示的IEEE33节点配电系统节点23处，快充站B位于图4所示的配电网节点7处。两站的快充桩数量分别为20和30，快充桩所能提供的最大充电功率为80kW，功率因数为98%。为了便于分析，系统运行状态取在其负荷较高的21∶00左右，功率变化向量取为一台电动汽车接入时的最大快充功率，即b=[0 … 0 80 0 … … 0 16.25 0 … 0]T，其中16.25表示电动汽车接入时的无功功率(kVar)，非零元位置与快充站所在节点编号相对应。

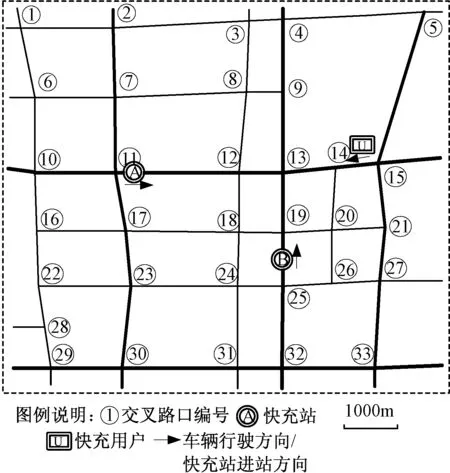
图3 目标区域主干道路交通网络示意图Fig.3 Transport network of trunk road in target area

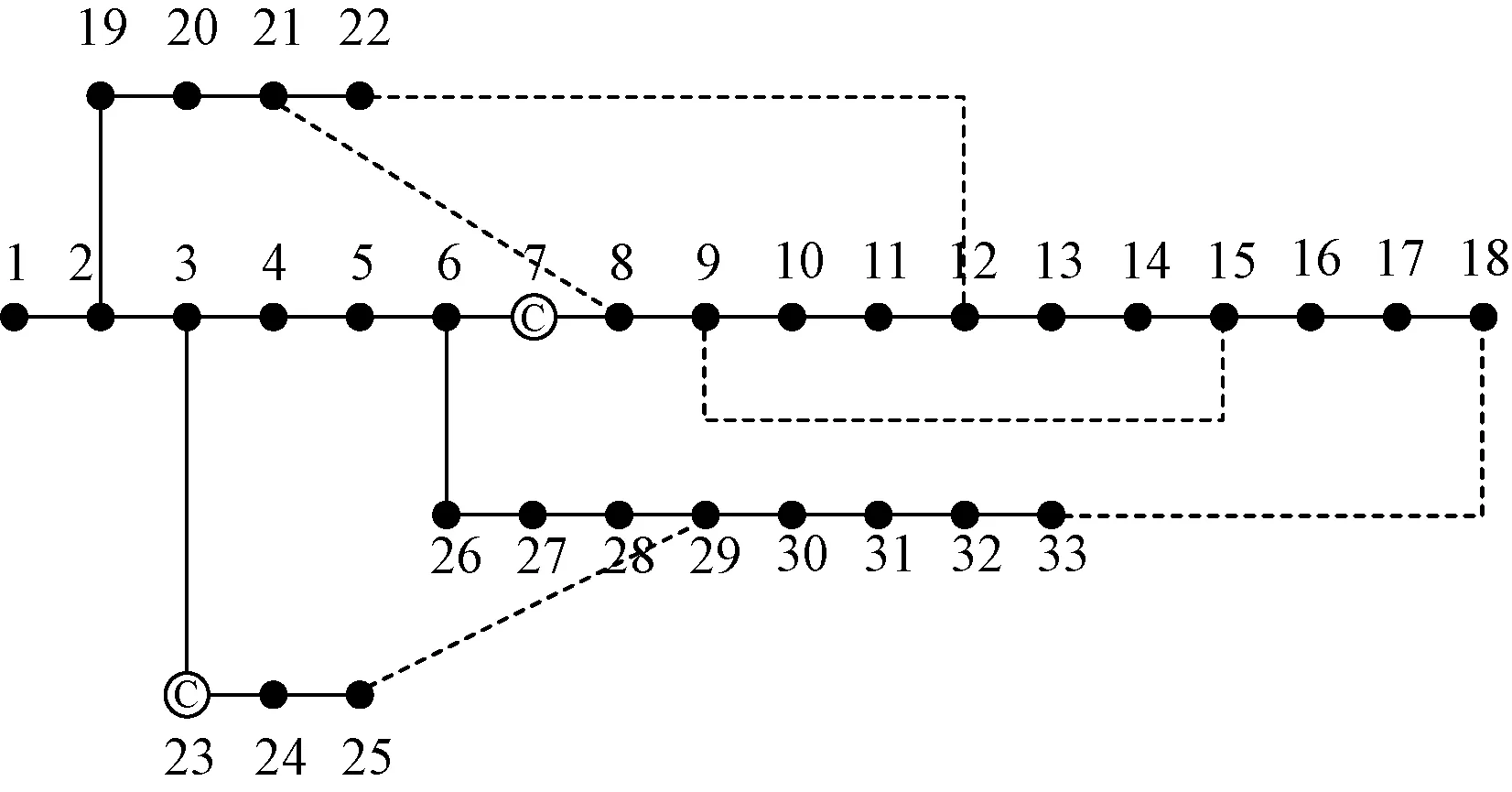
图4 IEEE 33节点配电系统Fig.4 IEEE 33 nodes distribution system

目标区域共有交叉路口33个，基于MATLAB图论工具，形成目标区域交通网络所对应的含33个顶点的有向带权图，如图5所示，其中标明了当前时段内各路段的交通状况。

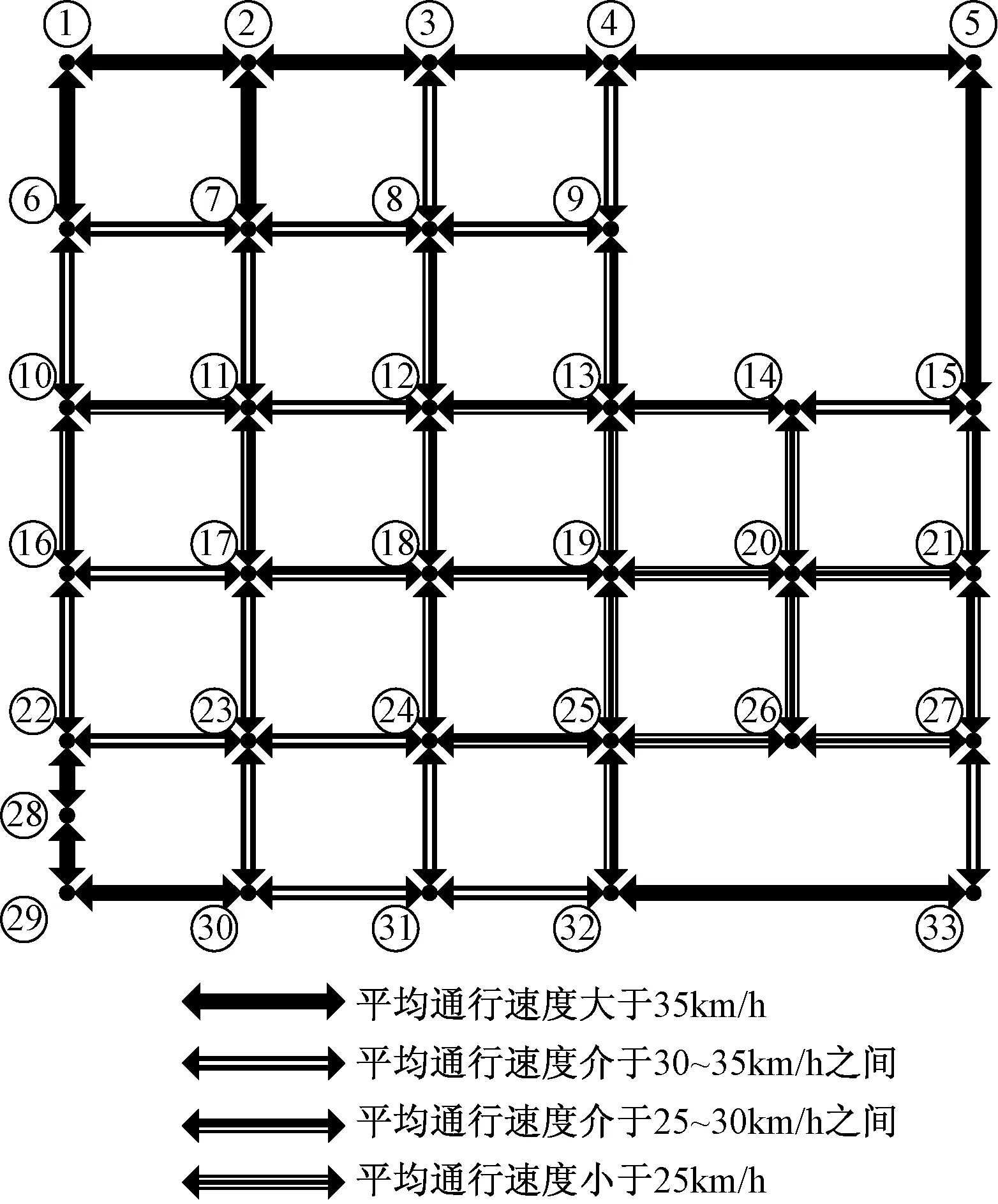
图5 目标区域交通网络形成的有向带权图及交通状况Fig.5 Directed weighted graph and traffic condition

4.2 两座快充站同时接入快充负荷时对应节点的配电系统电压可承受度

在快充站节点7单独加负荷，经计算发现，节点18一直为系统的电压最低点，绘制节点18的PV曲线如图6所示。

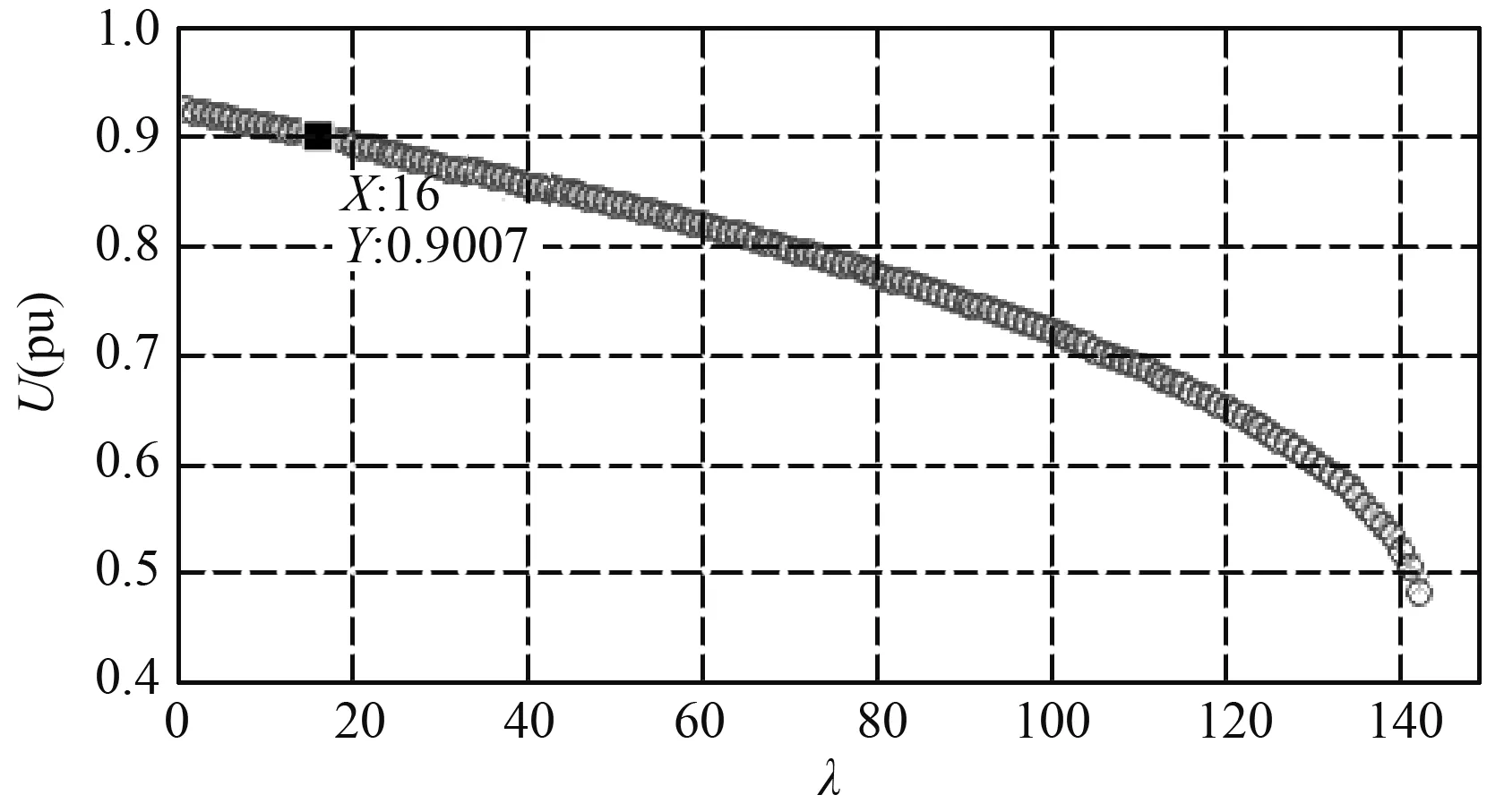
图6 节点18的PV曲线(在节点7增加快充负荷)Fig.6 PV curve of node 18 (increasing fast charge at node 7)

当根据电能质量的要求，电压幅值最低为0.9pu(电源节点1的电压为1.0pu)时，由图6可见，功率变化参数λ为16时，电压已经下降到限值附近，所以快充站节点7的快充功率接入限值为：

Pssm(7)=λb=16×80=1280kW

(9)

因此，充电站所在的7号节点的配电系统电压可承受度D为：

D(7)=Pssm(7)=1280kW

(10)

根据3.2节的分析，考虑快充桩位的限制，此时，7号节点充电站的快充桩所能提供的最小快充功率为：

(11)

同理，在快充站节点23单独加负荷时，计算发现节点18的电压率先达到电压幅值限值，此时的PV曲线如图7所示。

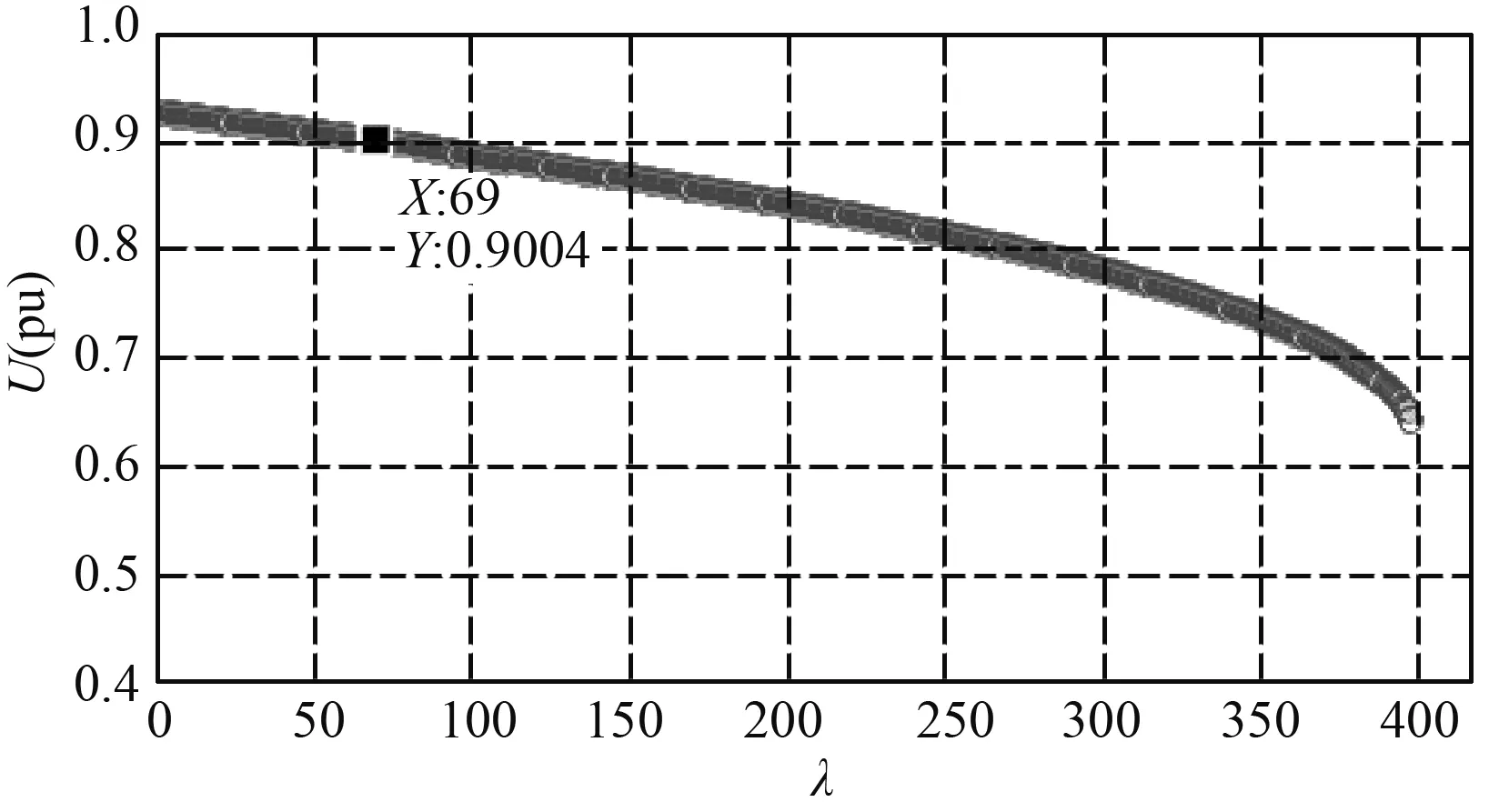
图7 节点18的PV曲线(在节点23增加快充负荷)Fig.7 PV curve of node 18 (increasing fast charge at node 23)

由图7可见，功率变化参数λ为69时，电压下降到限值附近，所以快充站节点23的快充功率接入限值为：

Pssm(23)=λb=69×80=5520kW

(12)

因此，23号节点充电站的配电系统电压可承受度D为：

D(23)=Pssm(23)=5520kW

(13)

考虑快充桩位的限制，此时，23号节点充电站的快充桩所能提供的最小快充功率为：

(14)

同理，当以不同的比例在两座快充站同时接入快充负荷时，两座快充站所在节点的配电系统电压可承受度数值变化如表1所示。

表1 两座快充站同时接入快充负荷时对应节点的配电系统电压可承受度Tab.1 Distribution system voltage tolerance with fast charge load accessing

可以看出，由于IEEE33节点配电系统馈线之间存在耦合线路，各节点之间的配电系统电压可承受度彼此之间相互牵制。当本节点的充电负荷比例较小时，意味着大量的充电负荷接入到其他的快充站，导致本节点的配电系统电压可承受度降低，且充电负荷比例越小，电压可承受度也越小。当充电负荷单独接入本节点时，该节点存在最大的配电系统电压可承受度，这个数值是由配电系统的网络参数和基础负荷水平决定的，不受充电负荷接入比例的影响，文后涉及的配电系统电压可承受度指代的即是该节点的最大配电系统电压可承受度。

4.3 基于电动汽车充电导航的快充负荷有序接入

以图3所示的用户为研究对象，该用户在图示位置产生快充需求，其行驶方向见图3，用户与下一个交叉路口14的距离为300m。车辆电池容量为15kW·h，当前SOC为35%，车辆的百公里耗电量为15kW·h。对于该用户而言，其充电位置选择过程为：通过充电导航系统车载终端，比对到快充站A和快充站B的最优路径所对应的属性值，最终决定充电导航方案。

基于3.1节的快充用户充电行为分析，对于I类用户，其考虑的属性值为路段长度，根据Dijkstra算法，其到A站和B站的最优路径如图8所示。由图8可知，电动汽车无序充电时，两方案对应的路段长度分别为：XA=4.75km、XB=2.83km。由于XB较小，用户选择到B站充电为其最佳充电方案。

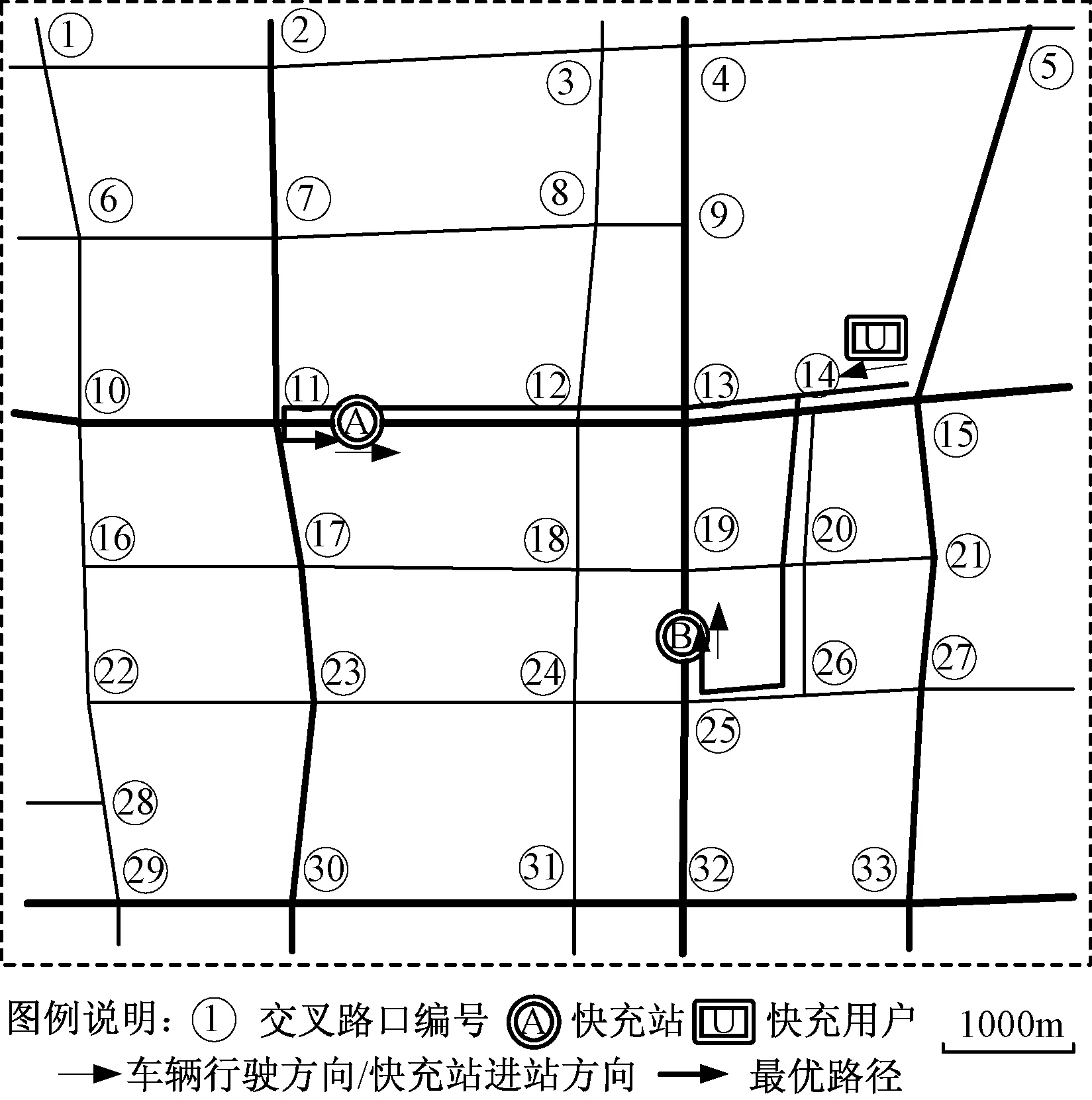
图8 I类用户到达A、B两座快充站的最优路径Fig.8 Optimal path when class I users arrive at A and B fast charge stations

对于II类用户，其考虑的属性值为充电总时间，将路段通行时间作为弧权，同样，根据Dijkstra算法，其到A站和B站的最优路径如图9所示。

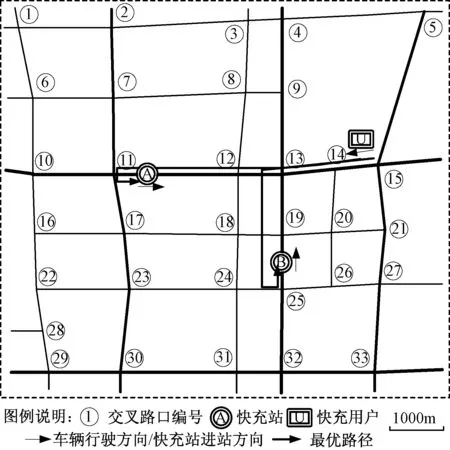
图9 II类用户到达A、B两座快充站的最优路径Fig.9 Optimal path when class II users arrive at A and B fast charge stations

两方案对应的到站时间分别为：XA=9.46min，XB=9.86min。结合4.2节的算例，快充站A的预期充电功率为80kW，快充站B的预期充电功率为72kW，考虑车辆行驶途中的电量消耗，在A、B两站的预期充电时间为：TcA=7.85min，TcB=8.48min。因此到A、B两站充电的总时间分别为：TdA=17.31min，TdB=18.34min。由于TdA较小，用户选择到A站充电为其最佳充电方案。

5 结论

目前的车辆导航系统没有考虑电网侧的影响，不完全适用于电动汽车充电导航，针对此问题，本文提出了考虑配电系统电压可承受度的电动汽车充电导航策略。从用户侧、电网侧、交通侧三个角度分析了电动汽车充电导航策略的形成，对于电网侧，提出了快充站所在节点的配电系统电压可承受度指标，并分析了快充桩相应的充电功率调节方法；对于交通侧，分析了基于Dijkstra算法的最优路径规划方法。该充电导航策略结合了交通侧和电网侧提供的信息，能够满足电动汽车用户的多样化需求，可为用户提供更全面的信息以及更优质的充电体验。

参考文献(References)：

[1] Boulanger A G，Chu A C，Maxx S，et al．Vehicle electrification：Status and issues[J]．Proceedings of the IEEE，2011, 99(6)：1116-1138．

[2] 欧阳明高(Ouyang Minggao)．我国节能与新能源汽车发展战略与对策(Chinese development strategy and countermeasure of energy-saving and new energy automotive)[J]．汽车工程(Automotive Engineering)，2006，28(4)：317-321．

[3] 吴憩棠(Wu Qitang)．我国“十城千辆”计划的进展(Progresses in “Ten Cities & Thousand Units” plan)[J]．新能源汽车(New Energy Vehicles)，2009，1(24)：15-19．

[4] Sortomme E，El-Sharkawi M A．Optimal charging strategies for unidirectional vehicle-to-grid[J]．IEEE Transactions on Smart Grid，2011，2(1)：131-138．

[5] 胡泽春，宋永华，徐智威，等(Hu Zechun，Song Yonghua，Xu Zhiwei，et al.)．电动汽车接入电网的影响与利用(Impacts and utilization of electric vehicles integration into power systems)[J]．中国电机工程学报(Proceedings of the CSEE)，2012，32(4)：1-10．

[6] Su W, Chow M Y. Performance evaluation of a PHEV parking station using particle swarm optimization[A]. 2011 IEEE Power and Energy Society General Meeting[C]. 2011. 1-6.

[7] Su W, Chow M Y. Performance evaluation of an EDA-based large-scale plug-in hybrid electric vehicle charging algorithm[J]. IEEE Transactions on Smart Grid, 2012, 3(1): 308-315.

[8] Su W, Chow M Y. Sensitivity analysis on battery modeling to large-scale PHEV/PEV charging algorithms[A]. IECON 2011 - 37th Annual Conference of the IEEE Industrial Electronics Society[C]. 2011. 3248-3253.

[9] Denholm P, Short W. An evaluation of utility system impacts and benefits of optimally dispatched[R]. National Renewable Energy Laboratory, 2006.

[10] 田立亭, 史双龙, 贾卓(Tian Liting，Shi Shuanglong，Jia Zhuo). 电动汽车充电功率需求的统计学建模方法(Evaluation and solutions for electric vehicles’ impact on the grid)[J]. 电网技术(Power System Technology), 2010, 34 (11): 126-130.

[11] Li G, Zhang X P. Modeling of plug-in hybrid electric vehicle charging demand in probabilistic power flow calculations[J]. IEEE Transactions on Smart Grid, 2012, 3(1): 492-499.

[12] 陈丽丹, 聂涌泉, 钟庆(Chen Lidan，Nie Yongquan，Zhong Qing). 基于出行链的电动汽车充电负荷预测模型(A model for electric vehicle charging load forecasting based on trip chains)[J]. 电工技术学报(Transactions of China Electrotechnical Society), 2015, 30(4): 216-225.

[13] 徐浩, 苗世洪, 钱甜甜, 等(Xu Hao，Miao Shihong， Qian Tiantian，et al.). 计及多日一充模式的规模化电动汽车充电负荷建模策略(A modeling strategy for charging loads of large-scale electric vehicles considering multi-days spaced charging mode)[J]. 电工技术学报(Transactions of China Electrotechnical Society), 2015, 30(9): 129-137.

[14] 葛少云，冯亮，刘洪，等(Ge Shaoyun，Feng Liang，Liu Hong，et al.)． 考虑用户便捷性的电动汽车充电站规划(Planning of electric vehicle charging stations considering users’convenience)[J]． 电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2014，33 (2): 70-75．

[15] 杨少兵, 吴命利, 姜久春, 等(Yang Shaobing，Wu Mingli，Jiang Jiuchun，et al.). 电动汽车充电站负荷建模方法(An approach for load modeling of electric vehicle charging station)[J]. 电网技术(Power System Technology), 2013, 37(5): 1190-1195.

[16] 王锡凡, 邵成成, 王秀丽, 等(Wang Xifan，Shao Chengcheng，Wang Xiuli，et al.). 电动汽车充电负荷与调度控制策略综述(Survey of electric vehicle charging load and dispatch control strategies)[J]. 中国电机工程学报(Proceedings of the CSEE), 2013, 33(1): 1-10.

[17] 中国电工技术学会电动车辆专业委员会(Electric Vehicle Committee，China Electrotechnical Society)．我国电动汽车市场化进程中相关问题综述(Annual report on technical and industrial development of electric vehicle power supply and drive in China)[J]． 电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2015，34 (7): 1-10．

[18] Geng B, Mills J K, Sun D. Coordinated charging control of plug-in electric vehicles at a distribution transformer level using the vTOU-DP approach[A]. 2012 IEEE Vehicle Power and Propulsion Conference (VPPC) [C]. 2012. 1469-1474.

[19] 黄润, 周鑫, 严正, 等(Huang Run, Zhou Xin, Yan Zheng, et al.). 计及电动汽车不确定性的有序充电调度策略(The controlled charging dispatch strategy by considering of the uncertainty of electric vehicles)[J]. 现代电力(Modern Electric Power), 2012, 29(3): 57-63.

[20] Sortomme E, Hindi M M, Macpherson S D J, et al. Coordinated charging of plug-in hybrid electric vehicles to minimize distribution system losses[J]. IEEE Transactions on Smart Grid, 2011, 2(1): 198-205.

[21] 荣雅君，杨伟，牛欢，等(Rong Yajun，Yang Wei，Niu Huan，et al.)． 基于 BP-EKF 算法的电动汽车电池管理系统 SOC 精准估计(Accurate estimation of SOC value of electric vehicle battery based on EKF algorithm optimized by BP neural network)[J]． 电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2015，34 (9): 22-28．

[22] 苏舒, 孙近文, 林湘宁, 等(Su Shu，Sun Jinwen，Lin Xiangning，et al.). 电动汽车智能充电导航(Electric vehicle smart charging navigation)[J]. 中国电机工程学报(Proceedings of the CSEE), 2013, 33(Suppl.): 59-67.

[23] Guo Q, Xin S, Sun H, et al. Rapid-charging navigation of electric vehicles based on real-time power systems and traffic data[J]. IEEE Transactions on Smart Grid, 2014, 5(4): 1969-1979.

[24] 祝达康, 程浩忠(Zhu Dakang，Cheng Haozhong). 求取电力系统 PV 曲线的改进连续潮流法(A modified continuation power system method for computing PV curve of power system)[J]. 电网技术(Power System Technology), 1999, 23(4): 36-40.

[25] 郭瑞鹏, 韩祯祥(Guo Ruipeng，Han Zhenxiang). 电压稳定分析的改进连续潮流法(An improved continuation power flow method for voltage stability analysis)[J]. 电力系统自动化(Automation of Electric Power Systems), 1999, 23(14): 13-16.