基于单相矢量控制的MMC环流抑制策略

吕泳庆， 邓富金， 王青松， 程 明

(东南大学电气工程学院， 江苏 南京 210096)

1 引言

近年来，模块化多电平变流器(Modular Multilevel Converter, MMC)在高压大容量的输电场合得到日益广泛的应用[1-4]，其具有良好的输出特性[5-8]及高效率[9,10]的优点。但MMC的交直流侧能量交换是一个动态平衡过程，这会引起桥臂子模块电容的周期性电压波动，进而引起桥臂电压周期性波动，产生相内环流，尤其以二倍频环流为主。二倍频环流对MMC输出功率无贡献，却增加了开关额定容量和通态损耗，也给MMC系统带来高次谐波扰动，影响系统的正常运行。因此，如何有效抑制MMC相内环流是其应用过程中的重要问题。

目前已有诸多文献针对MMC的相内环流问题进行了相关研究。文献[11]从开关函数的角度对MMC内子模块的电容电压波动及环流进行了数学分析，并定量给出了相内环流对MMC交直流测输出电流的谐波成分的影响，为环流抑制提供了相关理论依据。文献[12]从MMC瞬时能量平衡的角度对环流形成的机理进行了详细分析，并给出了通过增加桥臂电感的方法抑制相内环流的计算公式，但此方法无法从根本上消除环流，且会增加系统体积，提高系统成本。文献[13]通过三相矢量控制的方法，将三相二倍频环流矢量变换至同步旋转坐标系中，并采用比例-积分控制抑制相内环流，从而改善MMC的运行性能。

本文针对MMC的相内环流问题，提出了一种基于单相矢量控制的MMC二倍频环流抑制策略。该策略单独对MMC的每一相进行了二倍频环流的抑制，从而实现了整个系统的二倍频环流抑制的效果。另外，本文也给出了环流抑制器和系统整体控制框图。最后通过仿真软件PSCAD/EMTDC仿真验证了所提出控制策略的有效性和可行性。

2 MMC的拓扑结构及运行特性

2.1 MMC的拓扑结构

图1为三相MMC的拓扑结构。MMC由三相六桥臂构成，每相桥臂由N个相同的子模块(Sub-Module, SM)和上下桥臂电感Ls组成。图2为子模块的结构。子模块为半桥结构，两侧并联储能电容Csm，其稳态电压为uC。MMC正常运行时子模块有两种工作状态：①当T1导通T2关断时子模块投入，此时子模块输出电压等于电容电压uC；②当T1关断T2导通时子模块切除，此时子模块输出电压等于0。子模块投入时，电容Csm的充放电取决于其所在的桥臂电流的方向。若桥臂电流iuj或ilj(j=a, b, c)方向为正(见图1)，则此时子模块电容充电，uC升高；若桥臂电流iuj或ilj方向为负，则此时子模块电容放电，uC降低。子模块切除时，相应的电容从MMC中被旁路，此时无论桥臂电流方向为正或负uC均不变。

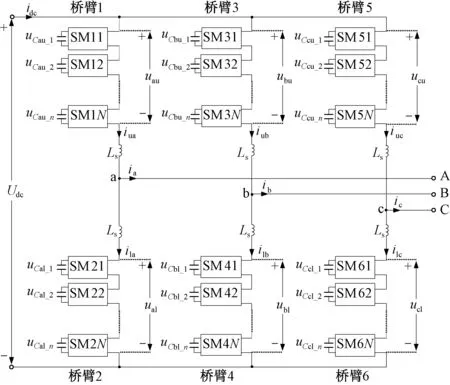
图1 三相MMC的拓扑结构Fig.1 Circuit of three-phase MMC

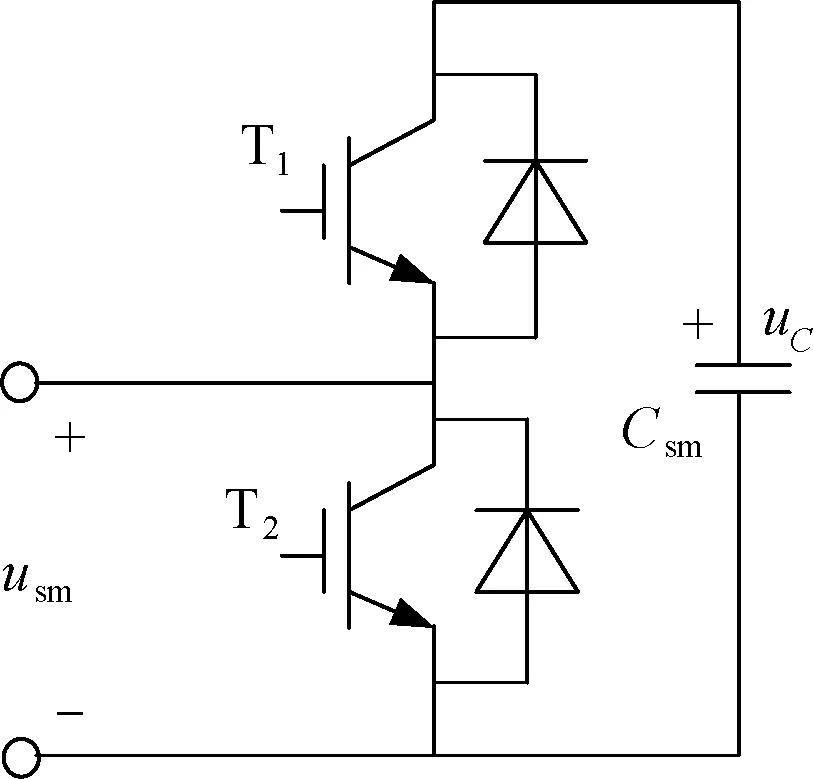
图2 子模块的结构Fig.2 Structure of SM unit

2.2 MMC电压平衡控制

MMC由大量子模块串联组成，为保证MMC正常运行，需要引入适当的控制策略实现子模块间电容电压的平衡。以实现A相上桥臂电容电压平衡为例，图3为MMC电容电压平衡控制原理示意图。通过实时监测采样获得A相上桥臂各子模块的电容电压uCau_1～uCau_n和A相上桥臂电流iua，并根据子模块电容电压uCau_1～uCau_n对A相上桥臂子模块进行堆栈排序。通过采用载波移相-正弦脉宽调制方式(Carrier Phase Shift-Sinusoidal Pulse Width Modulation, CPS-SPWM)获得需要投入的子模块数目nua。当A相上桥臂电流iua方向为正，则投入电容电压最低的nua个子模块；若桥臂电流iua方向为负，则投入电容电压最高的nua个子模块[14,15]。如此便可实现A相上桥臂子模块间电容电压的平衡。其他桥臂电容电压平衡控制方法与此类似。

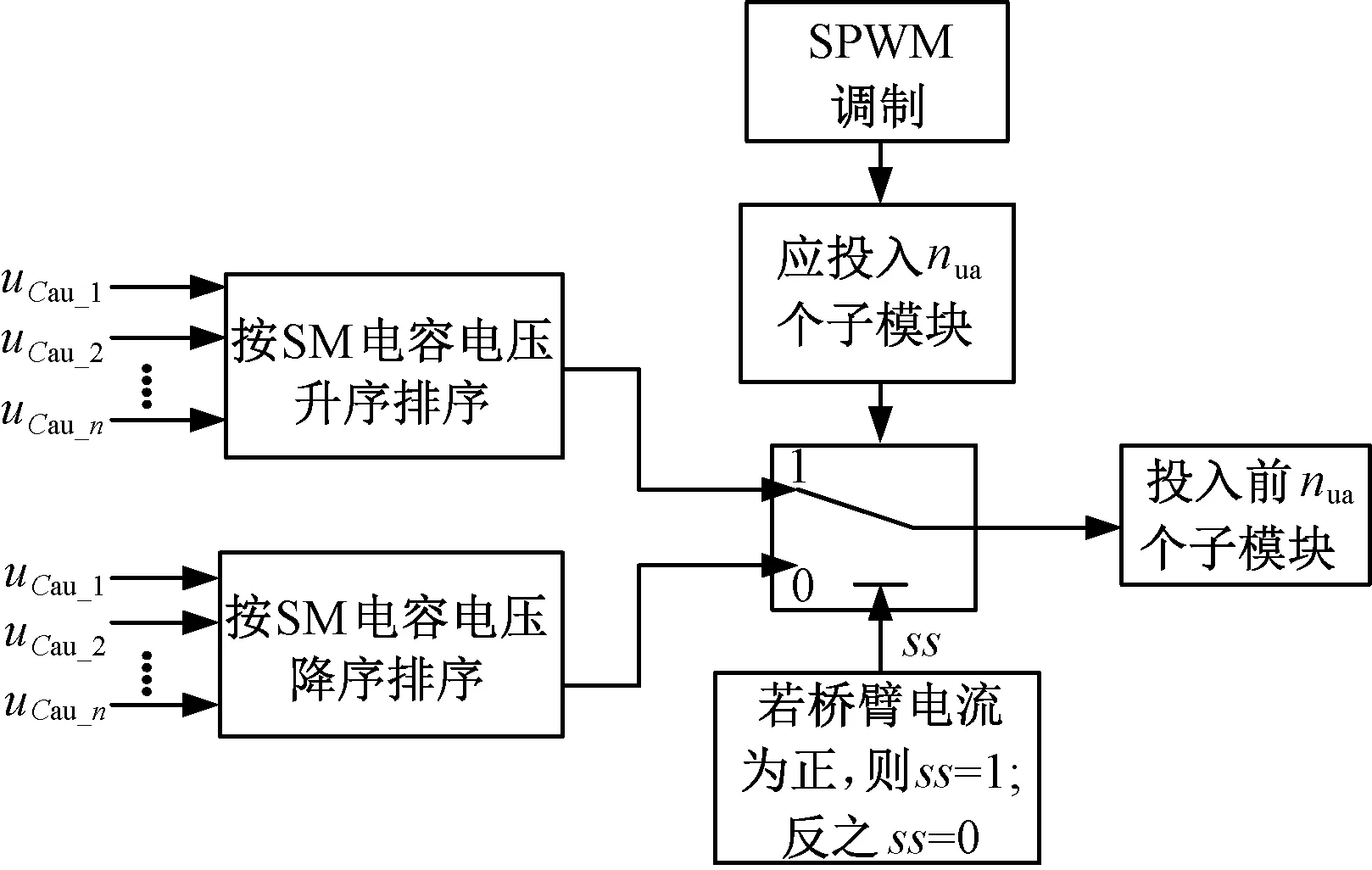
图3 子模块均压原理Fig.3 Principle of voltage-balancing control

3 MMC环流机理分析及其抑制策略

本节首先分析MMC相内谐波环流产生的机理，然后针对相内二倍频环流，提出了一种基于单相矢量控制的环流控制策略，详细给出了控制思想及系统控制的结构框图，并结合MMC的功率控制器完成MMC控制系统的整体设计。

3.1 MMC的环流分析

MMC正常工作时会在相内流过环流，以二倍频环流为主。为简化分析过程，这里以A相桥臂电流为例分析二倍频环流产生的机理。首先假设桥臂电流的主要成分为基频交流分量和直流分量，其分别流入到交流电网和直流母线中。设A相变流器输出的基频电流和电压为：

(1)

(2)

式中，Ia和Ua为A相变流器输出电流和电压的有效值；ω为基频角频率；φ为基频功率因数角。则A相上下桥臂电流可表示为：

(3)

式中，Iad为A相桥臂电流直流分量。流入A相上下桥臂子模块的平均电容电流iCap_ua、iCap_la分别为[16,17]：

(4)

(5)

式中，ya=msinωt；m为调制比，m=2Ua/Udc，Udc为直流母线电压。

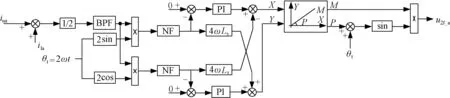
图4 单相矢量控制的二倍频环流控制器Fig.4 Circulating current controller based on single phase vector control

由式(4)、式(5)可知，桥臂中基频电流分量会引起子模块中的二倍频电流波动。上下桥臂子模块的端口电压可表示为：

(6)

则上下桥臂电压可以表示为：

(7)

式中，nua和nla分别为上下桥臂投入的子模块数。

联立式(4)～式(7)，略去高次谐波分量，得A相桥臂二倍频波动电压为[18]：

(8)

式中，N为上、下桥臂子模块数。

A相桥臂内的二倍频电压波动会引起A相内二倍频环流。同时由式(4)～式(7)可知，子模块与桥臂电气量是循环耦合的，二倍频相内环流会进一步在MMC桥臂及子模块中引起高次谐波扰动。因而抑制相内二倍频环流对提高MMC的可靠性，降低开关管容量及通态损耗是很重要的。

3.2 基于单相矢量的环流控制

以A相为例，忽略桥臂电流内的高次谐波分量，则A相上下桥臂电流iua、ila可以表示为：

(9)

式中，ia为A相交流侧基频输出电流；i2f_a为A相桥臂内二倍频环流分量。由图1可知，A相内二倍频环流会在桥臂电感Ls上产生二倍频电压u2f_a，两者之间的关系可表示为：

(10)

根据单相时序坐标系与d-q同步旋转坐标系间的变换规则，式(10)所示的A相桥臂内二倍频时域环流特性在d-q二倍频同步旋转坐标系中可表示为：

(11)

式中，u2f_a_d、u2f_a_q和i2f_a_d、i2f_a_q分别为二倍频同步旋转坐标系下A相桥臂电感上的二倍频电压u2f_a和A相内二倍频环流i2f_a的dq分量。

根据式(11)，本文设计了基于单相矢量控制的二倍频环流抑制器，如图4所示。由式(9)可得到A相内环流，带通滤波器中心频率设定为二倍基频，以滤除其中的直流分量得到i2f_a。将得到的i2f_a与变换信号2sin2ωt、2cos2ωt分别相乘可实现单相同步旋转坐标变换。再将得到的信号通过中心频率为四倍基频的陷波器便可得到i2f_a的直流dq分量i2f_a_d、i2f_a_q。其中带通滤波器及陷波器的传递函数可以表示为：

(12)

(13)

式中，k为实常数，其值决定了滤波器及陷波器的频率特性。图4中，由网侧锁相环(PLL)可以得到电网的基频相位θt和基频角频率ω。在单相矢量控制的基础上采用闭环比例-积分控制便可将i2f_a_d、i2f_a_q均抑制为零。

3.3 MMC控制系统的整体设计

基于3.1节和3.2节的分析可以得到带有单相矢量环流抑制控制的MMC系统控制结构，如图5所示。其中ua、ub、uc及ia、ib、ic分别为电网电压和电网电流，而ud、uq及id、iq分别为其三相基频同步旋转坐标系下的dq分量。L=Ls/2+Lf，其中Lf为网侧滤波电感。根据MMC输出的有功功率、无功功率的控制要求可以得到交直轴电流的参考值id_ref和iq_ref，同时通过三相矢量控制便可得到三相桥臂电压调制波的参考值uj_ref[13]。在此参考调制波基础上叠加单相矢量环流抑制器输出的二倍频补偿电压u2fj，便可有效抑制二倍频环流。

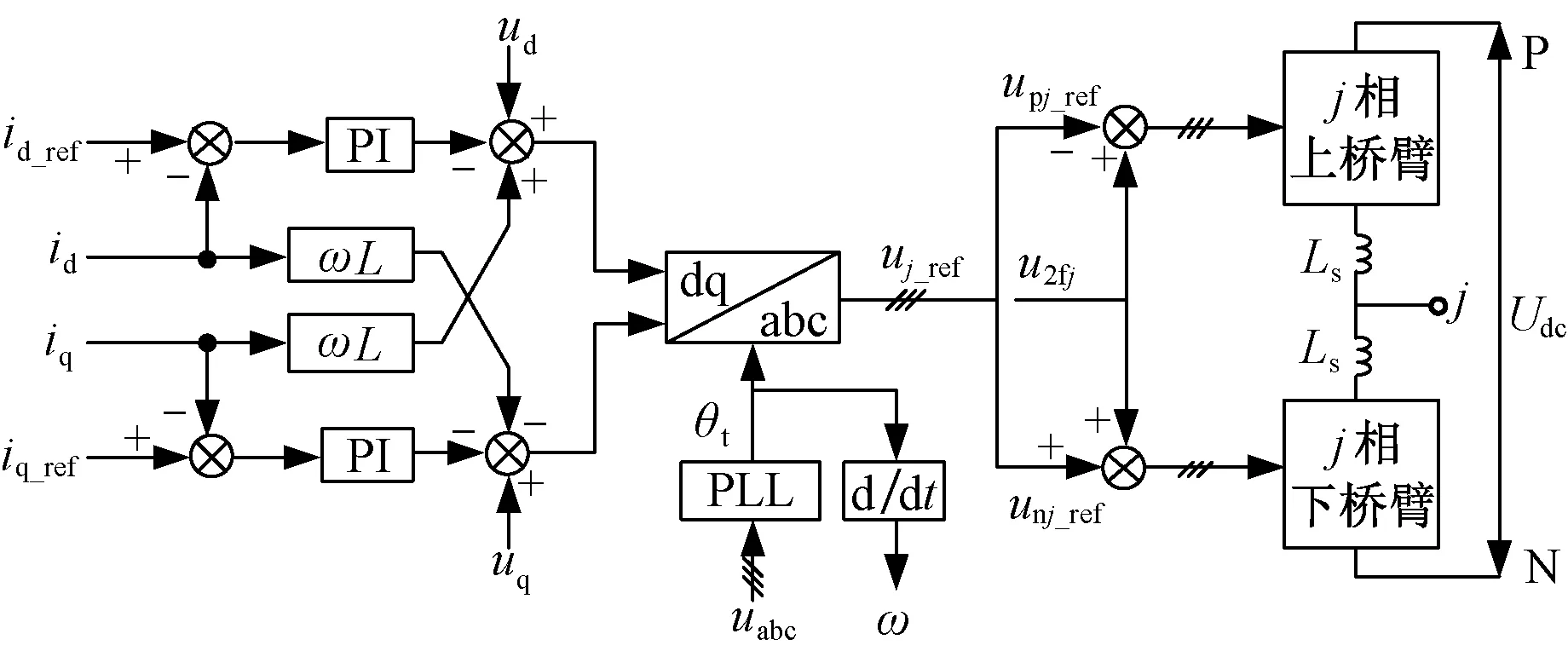
图5 MMC系统控制结构Fig.5 Control structure of MMC

4 仿真验证

为了验证基于单相矢量控制的MMC环流抑制策略的可行性，在PSCAD/EMTDC中搭建了三相MMC仿真模型进行仿真分析。MMC调制方式采用CPS-SPWM方式。给定MMC正常运行时向电网输出有功功率15MW,输出无功功率1.5MVar。其他MMC的相关仿真参数如表1所示。

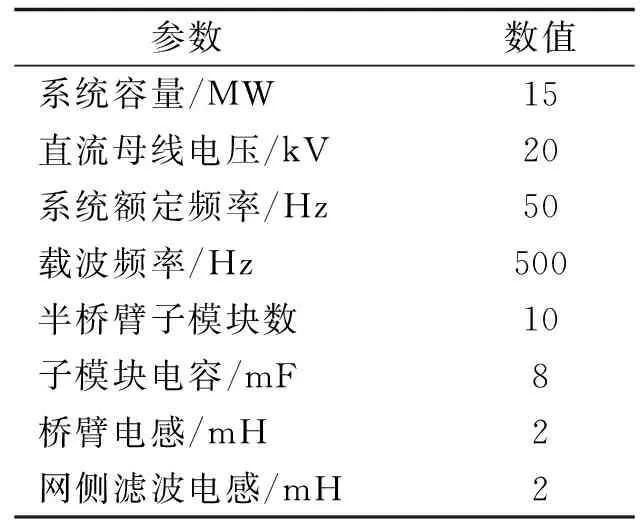
表1 仿真参数Tab.1 Experimental parameters

图6(a)为未投入单相矢量控制环流控制器时A相上下桥臂电流及环流波形图。可以看出，受相内环流的干扰，A相桥臂电流出现严重的波形畸变；环流分量主要为直流分量与二倍频成分，与3.1节的分析一致。图6(b)与图6(c)分别为B、C两相上下桥臂电流及环流波形图，与A相结果相似。图6(d)为此时A相上下桥臂SM的电容电压波形图，电容电压脉动较大，约为0.4kV。

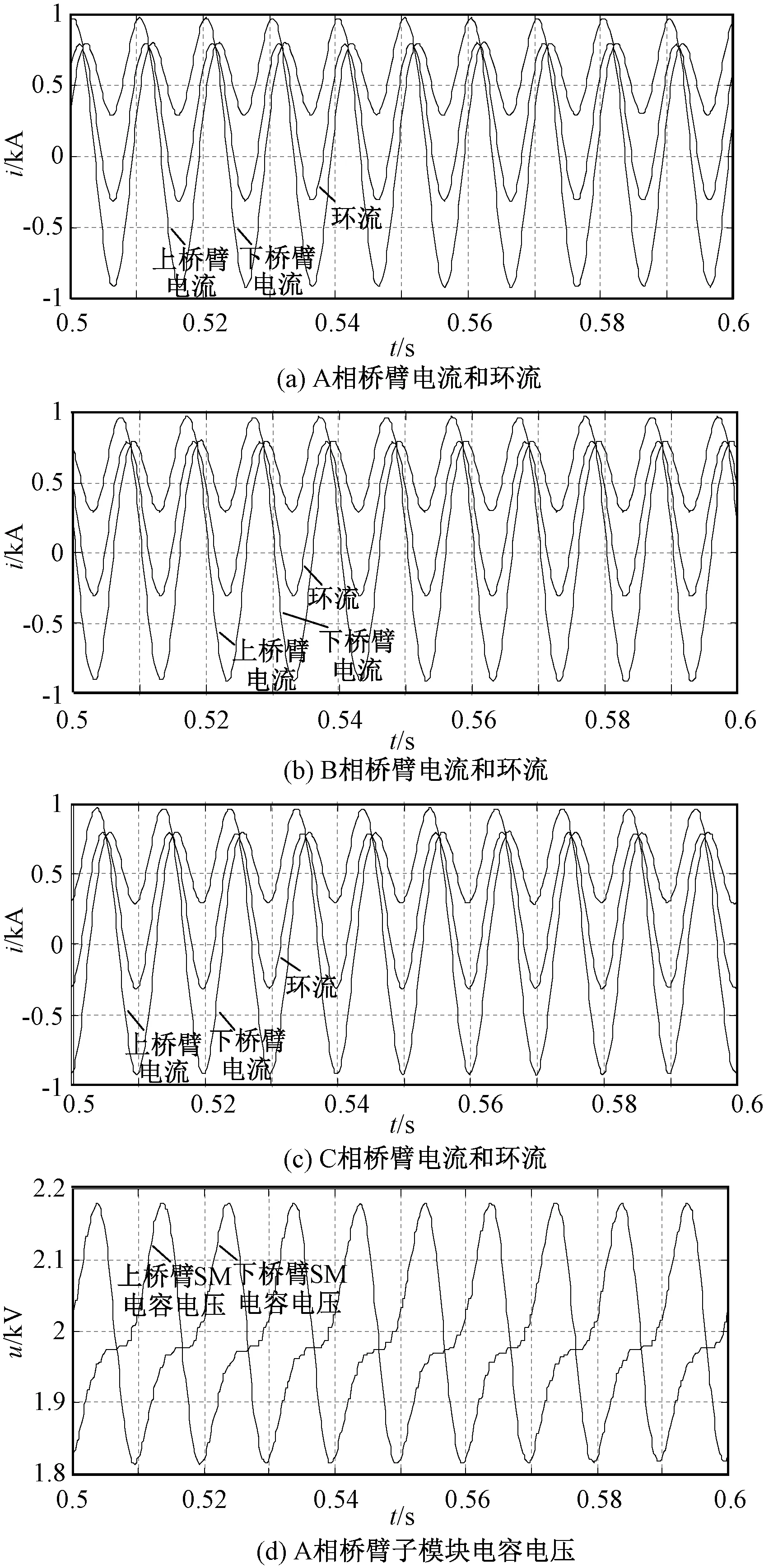
图6 投入环流控制器前波形Fig.6 Waveforms before circulating current control

图7(a)为投入单相矢量控制环流控制器后A相上下桥臂电流及环流波形图。可以看出，二倍频环流分量得到了有效的抑制，相内环流基本上只有直流分量；A相桥臂电流波形有了明显的改善，波形接近基频正弦波。图7(b)与图7(c)分别为此时B、C两相上下桥臂电流及环流波形图，与A相有相似的控制效果。图7(d)为此时A相上下桥臂SM的电容电压波形图，可以看出电容电压波动明显减小，约为0.2kV。由此可见，采用本文提出的单相矢量控制策略抑制相内二倍频环流是可行且有效的。

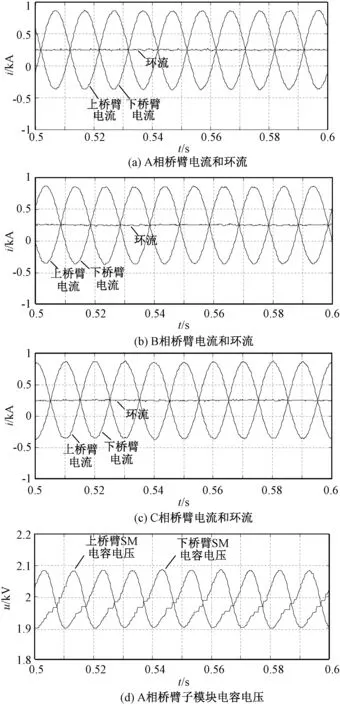
图7 投入环流控制器后波形Fig.7 Waveforms after circulating current control

5 实验验证

三相MMC实验样机参数如表2所示。子模块中的功率开关管采用标准IXFK48N60P型功率MOSFET，主电路核心数字信号控制器采用dSPACE1006，其产生的信号经光纤传输到各个子模块的驱动板，从而控制各个子模块的投入和切除。

图8为未投入单相矢量控制环流控制器时A相的上下桥臂电流、环流及交流侧输出电流的实验波形。可以看出，受相内环流的干扰，A相桥臂电流

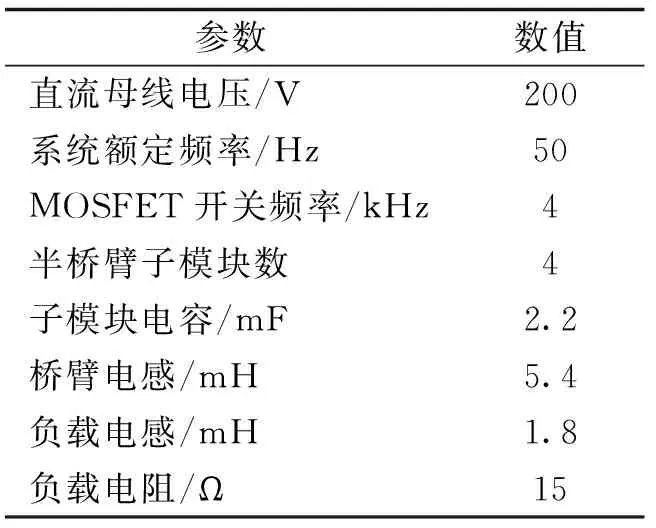
表2 实验参数Tab.2 Experimental parameters

出现严重的波形畸变。图9为投入单相矢量控制环流控制器时A相的上下桥臂电流、环流及交流侧输出电流的实验波形。可以看出，此时A相内二倍频环流得到了有效的抑制，基本上只有直流分量；桥臂电流波形得到了明显的改善。实验结果验证了本文所提出的单相矢量环流控制策略的可行性。

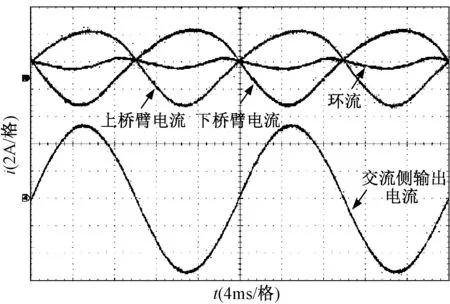
图8 投入环流控制器前实验波形Fig.8 Experimental waveforms before circulating current control

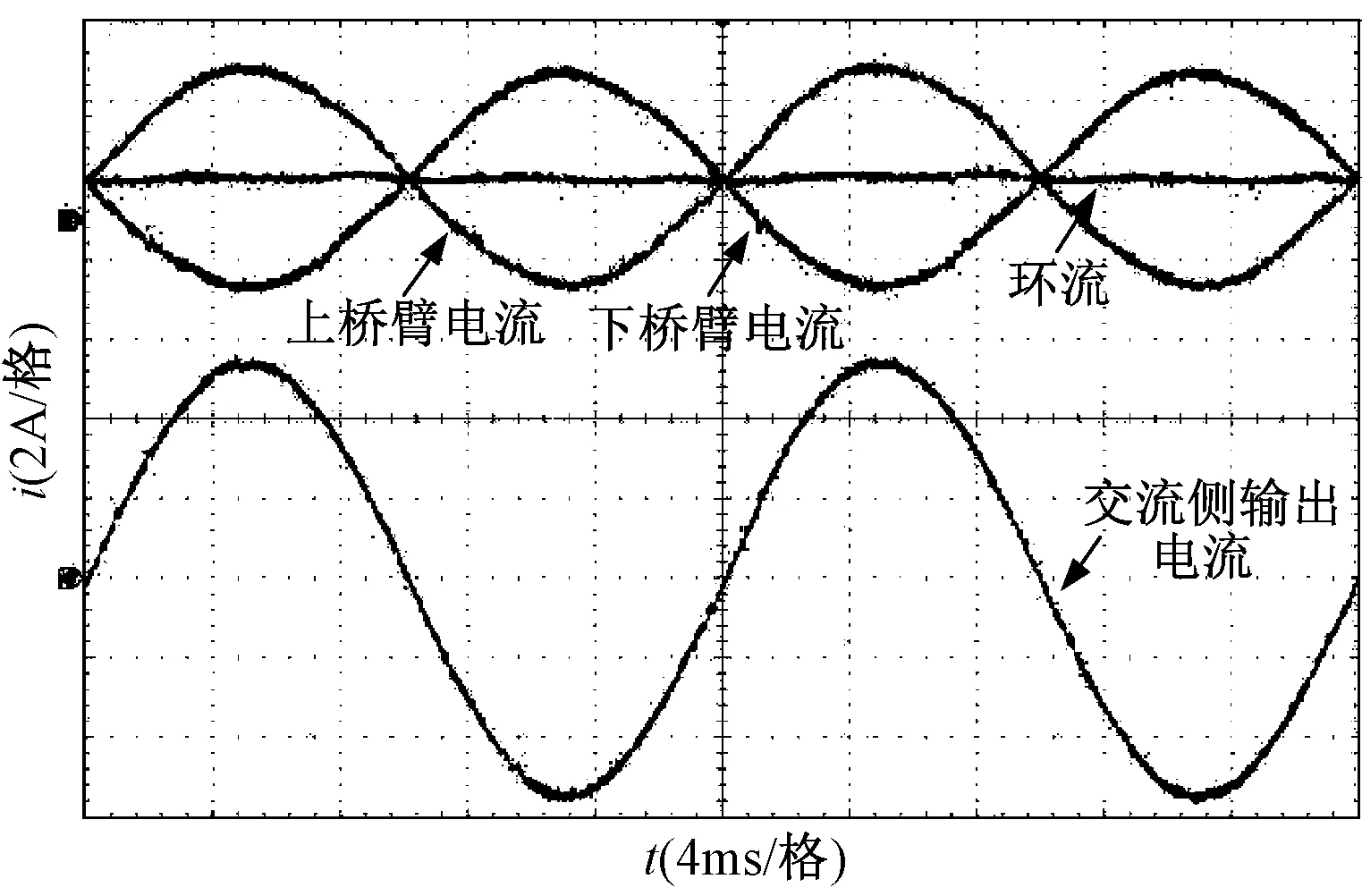
图9 投入环流控制器后实验波形Fig.9 Experimental waveforms after circulating current control

6 结论

本文从三相MMC的拓扑结构及运行特性出发，推导证明了相内二倍频环流的存在及其产生的机理。为了抑制相内二倍频环流，本文提出了一种基于单相矢量控制的环流抑制策略，对各相桥臂电压进行补偿调制以抑制二倍频环流。仿真和实验结果表明所提出的单相矢量控制方法能够有效地抑制各相内的二倍频环流，进而能够有效改善桥臂电流波形。

参考文献(References)：

[1] 周廷东，徐永海(Zhou Tingdong, Xu Yonghai).基于MMC的配电网电力电子变压器故障特性分析(Fault characteristic analysis of power electronic transformer based on MMC in distribution network)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2017, 36(5): 34-41.

[2] 杨晓峰，林智钦，周楚尧，等(Yang Xiaofeng, Lin Zhiqin, Zhou Chuyao, et al.). 模块化多电平换流器MMC的环流抑制技术综述(Survey of circulating current suppressing technologies in MMC)[J]. 电源学报(Journal of Power Supply), 2015, 13(6): 59-67.

[3] 马文忠，孙迎新，武琳，等(Ma Wenzhong, Sun Yingxin, Wu Lin, et al.). MMC子模块电容电压改进控制方法的研究(Research on improved balance control for sub-module capacitor voltage for modular multilevel converter(MMC))[J].电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2016, 35(11): 53-58.

[4] Lives K, Antonopoulos A, Norrga S, et al. Steady-state analysis of interaction between harmonic components of arm and line quantities of modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2012, 27(1): 57-68.

[5] Kouro S, Malinowski M, Gopakumar K, et al. Recent advances and industrial applications of multilevel converters[J]. IEEE Transactions on Industrial Electronics, 2010, 57(8): 2553-2580.

[6] Rodriguez J, Bernet S, Wu B, et al. Multilevel voltage-source-converter topologies for industrial medium-voltage drives[J]. IEEE Transactions on Industrial Electronics, 2007, 54(6): 2930-2945.

[7] Song Q, Liu W, Li X, et al. A steady-state analysis method for a modular multilevel converter[J]. IEEE Transactions on Power Electronics, 2013, 28(8): 3702-3713.

[8] Hassanpoor A, Angquist L, Norrga S, et al. Tolerance band modulation methods for modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2015, 30(1): 311-326.

[9] Malinowski M, Gopakumar K, Rodriguez J, et al. A survey on cascaded multilevel inverters[J]. IEEE Transactions on Industrial Electronics, 2010, 57(7): 2197-2206.

[10] Harnefors L, Antonopoulos A, Norrga S, et al. Dynamic analysis of modular multilevel converters[J]. IEEE Transactions on Industrial Electronics, 2013, 60(7): 2526-2537.

[11] 周月宾，江道灼，郭捷，等(Zhou Yuebin, Jiang Daozhuo, Guo Jie, et al.). 模块化多电平换流器子模块电容电压波动与内部环流分析(Analysis of sub-module capacitor voltage ripples and circulating currents in modular multilevel converters)[J]. 中国电机工程学报(Proceedings of the CSEE), 2012, 32(24): 8-14.

[12] 屠卿瑞，徐政，郑翔，等(Tu Qingrui, Xu Zheng, Zheng Xiang, et al.).模块化多电平换流器型直流输电内部环流机理分析(Mechanism analysis on the circulating current in modular multilevel converter based HVDC)[J].高电压技术(High Voltage Engineering), 2010, 36(2): 547-552.

[13] 屠卿瑞，徐政，管敏渊，等(Tu Qingrui, Xu Zheng, Guan Minyuan, et al.). 模块化多电平换流器环流抑制控制器设计(Design of circulating current suppressing controllers for modular multilevel converter)[J]. 电力系统自动化(Automation of Electric Power Systems), 2010, 34(18): 57-61.

[14] Glinka M, Marquardt R. A new AC/AC multilevel converter family[J]. IEEE Transactions on Industrial Electronics, 2005, 52(3): 662-669.

[15] Rohner S, Bernet S, Hiller M, et al. Modulation, losses, and semiconductor requirements of modular multilevel converters[J]. IEEE Transactions on Industrial Electronics, 2010, 57(8): 2633-2642.

[16] Meshram P, Borghate V. A simplified nearest level control (NLC) voltage balancing method for modular multilevel converter (MMC)[J]. IEEE Transactions on Power Electronics, 2015, 30(1): 450-462.

[17] Pou J, Ceballos S, Konstantinou G, et al. Circulating current injection methods based on instantaneous information for the modular multilevel converter[J]. IEEE Transactions on Industrial Electronics, 2015, 62(2): 777-788.

[18] 宋强，饶宏(Song Qiang, Rao Hong). 柔性直流输电换流器的分析与设计(Analysis and design of the converters in VSC-HVDC system)[M]. 北京：清华大学出版社(Beijing: Tsinghua University Press)，2015.