微电网中电力电子变压器的电压质量控制策略研究

涂春鸣， 肖 凡， 兰 征， 袁靖兵

(国家电能变换与控制工程技术研究中心， 湖南大学， 湖南 长沙 410082)

1 引言

随着光伏、风电等新能源的大力发展，其波动性、间歇性、随机性等对电网的运行带来巨大挑战[1,2]。为了大量可靠地消纳新能源，将分布式新能源与本地负荷构成微电网成为目前消纳新能源的主要方式之一。对于微电网而言，电力电子变压器(Power Electronic Transformer, PET)为其提供了多种形式电能同时接入与消纳的能力，从而使得电力电子变压器作为微电网接口成为研究的热点[3]。

电力电子变压器是一种将电力电子变流技术与高频变压技术相结合的全新一代智能变压器，具备故障隔离、谐波隔离、无功补偿和充当微电网接口等功能。同时，电力电子变压器较好地回避了传统变压器存在的磁饱和、直流偏磁、空载损耗大等问题，具有实际工程应用价值[4,5]。目前，针对电力电子变压器的拓扑结构[6-11]、功率控制[12,13]、均压均流[14,15]等方面已有较多研究。电力电子变压器作为微电网与主电网之间的枢纽装备时，其能量管理与协调潜力也得到了广泛关注。文献[12]探讨了基于电力电子变压器的交直流混合微电网能量管理策略，对多电能形式微电网间的能量管理提供了较好的方案；文献[16]研究了电力电子变压器与光伏系统协调运行的控制策略；文献[17,18]研究了电力电子变压器与储能系统的协调策略。

电力电子变压器替代固态开关与传统变压器后，由于其内部多个直流环节的存在，使得微电网与主网间实现了完全的电气隔离，且隔断了微电网与主电网间的谐波交互通路。调研已有文献发现针对基于电力电子变压器的微电网的研究多集中在能量调节与管理，其作为微电网接口替代固态开关或传统变压器后可能引起的供电电压质量问题缺少关注。

虽然目前针对PET供电电压质量的研究较少，但针对其他变流器供电系统的电能质量问题已有大量研究[19-24]。文献[21]提出了基于多谐振控制器的谐波抑制方法，对谐波电流与不平衡问题提供了可行的治理方案。文献[22]提出了一种谐波电流旁路法来抑制输出电压中的谐波成分，但所提控制策略的参数选取偏复杂，需要合理权衡参数才能达到较好效果。文献[23]提出通过阻抗匹配与下垂控制结合减小微电网PCC点电压畸变率的方法，但所提方法较依赖负荷阻抗类型，需测量各频次谐波阻抗确定下垂控制方程。文献[24]所提的谐波下垂控制策略虽然不依赖阻抗类型，但各次谐波下垂系数计算复杂，匹配难度较大。这些研究对变流器供电系统的电压质量问题解决提供了较多方案，但PET在供电系统中的位置和作用与其他变流器存在明显差异，在选择控制策略时须有特殊的偏重。

基于以上分析，本文充分挖掘了PET电压质量调节的机理，提出了一种适用于PET的电压质量控制策略。所提方法无需考虑PCC点非线性负荷类型与分布情况，调节效果对系统运行状态不敏感。本文首先介绍了PET的基本原理，并详细分析了PET作为微电网接口后其输出侧PCC点电压质量的特征；然后，分析了PET调控PCC点电压质量的机理，提出了考虑PET输出级采样特点与容量等因素的高供电电压质量控制策略，实现了对PCC点电压质量的有效调节；仿真与实验结果证明了本文理论研究的正确性与可行性。

2 基于PET的微电网谐波特性分析

2.1 PET简介

三级式PET是目前研究的主流拓扑结构，如图 1 所示。该拓扑包括输入级、中间级和输出级三个部分。输入级主要包括级联H桥(Cascaded H-Bridge，CHB)[8,9]和模块化多电平变流器(Modular Multilevel Converter，MMC)[10,11]两种主流拓扑，实际中各级联单元硬件参数差异所导致的直流侧电压不相等和各级传输功率不均衡等已成为现有研究的热点问题[15]。对于中间级，现有拓扑多采用双主动桥(Dual Active Bridge，DAB)[25,26]或者单主动桥(Single Active Bridge，SAB)[27]。其中DAB的双向功率传输能力，对于PET多个端口间的能量管理与协调具有重要意义。输出级普遍采用电压源型逆变(Voltage Source Inverter，VSI) 结构，可以实现输出侧交流系统与PET低压直流母线间能量的灵活交互。

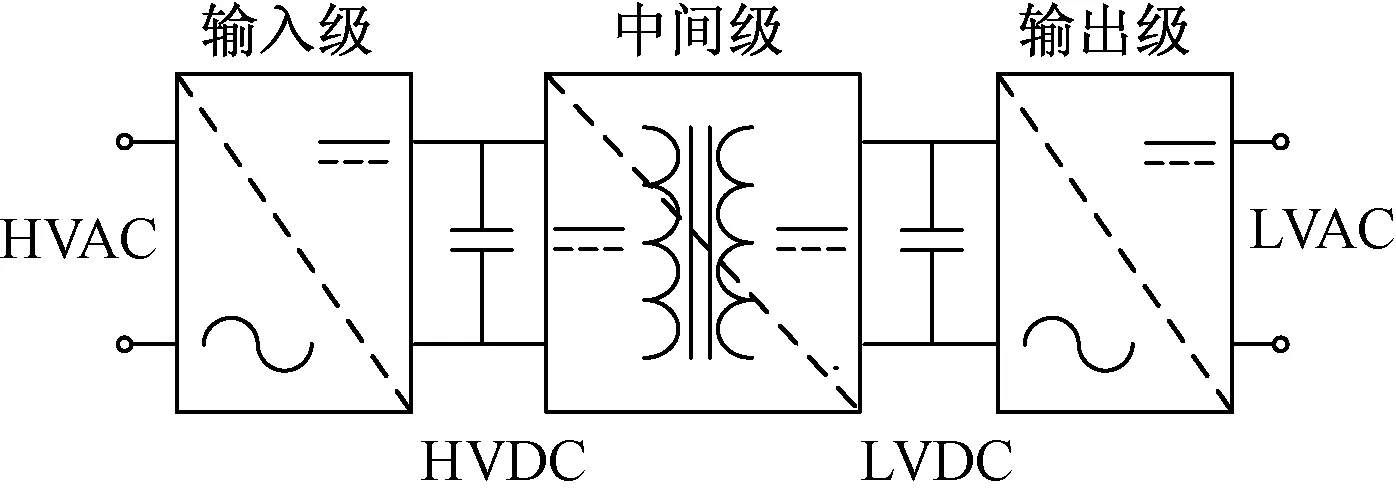
图1 三级式PET结构图Fig.1 Topology of PET with three stages

三级式PET的控制策略主要包括四种：①输入级控制并网电流和高压直流侧总电压(HVDC)，中间级控制低压直流母线电压、各DAB间的功率平衡、高压侧各模块的电压平衡，输出级控制输出电压或电流；②输入级控制并网电流和低压直流电压，中间级控制高压侧各模块电压和各DAB间的功率平衡，输出级控制低压输出电压或者电流；③输入级控制并网电流，中间级控制高压侧各级电压和各DAB间的功率平衡，输出级控制低压直流母线电压和输出侧并网电流；④输入级控制并网电流，中间级控制低压直流母线电压和各DAB间的功率平衡，输出级控制高压直流侧的总电压和输出的交流并网电流。

策略1、2与策略3、4的一个主要区别在于输出级控制为电压源或者电流源，本文将针对PET作为主电源供电情况下的供电电压质量问题进行分析与研究，输出级的控制策略采用电压源型控制策略，后文将不再进行相关的解释。

2.2 PET接入微电网后的电压质量问题分析

传统变压器常用于连接两个电压等级不同的系统，其负荷可分为线性负荷与非线性负荷两大类。进行电压等级归一化后，传统变压器可以近似等效为一个感抗。图2(a)为PET代替传统变压器后的配电网系统结构图。电力电子变压器内部多个直流环节的存在使得谐波电流难以穿过PET流入高压交流侧，谐波将在低压配电网内部流动，如图2(b)所示。

图2 含PET的系统谐波域等效图Fig.2 Equivalent harmonic circuit of grid with PET

此时PCC点谐波电压可表示为:

(1)

式中，VPCC为PCC点电压；Vh为谐波电压；Ih为谐波电流；ZL_V和ZL_C分别为电压源与电流源内阻；ZL为线性负荷等效阻抗；ZPET为PET等效阻抗。由式(1)可见， PCC点电压质量与PET输出级的等效谐波阻抗直接相关。图3为PET输出级的经典控制框图。其中，iout为PET输出电流，包括基波分量iof与谐波分量ioh。根据图3可得PET的输出模型为：

Uout(s)=GV(s)Uref-Zof(s)iof-Zoh(s)ioh

(2)

式中

(3)

(4)

其中，GU(s)为电压环增益函数，采用PI控制；GI(s)为电流环比例增益函数；KPWM为调制增益；Zof(s)为PET输出侧的基波等效输出阻抗，即基波阻抗；Zoh(s)为PET谐波等效输出阻抗，即谐波阻抗，其表达式与Zof(s)相同。式(2)中第一部分与第二部分均为基波分量，不会产生谐波电压；式(2)的第三部分包含谐波电流与谐波阻抗两个部分，是造成PET输出侧PCC点电压质量下降的主要因素。

图3 PET输出级控制框图Fig.3 Control sketch of output-stage

2.3 无电压质量调节下的PET仿真分析

图4为采用PI控制的PET与主电网系统阻抗对比图，共对比了三种不同等效电抗值下的主电网系统阻抗与PET阻抗在全频域上的分布差异。可以看出，在一定频率范围内主电网系统阻抗都明显小于PET的阻抗，此时PET供电电压质量将比传统变压器差。为了直观分析PET替代固态开关接入交流系统后高、低压侧的电压、电流情况，利用MATLAB仿真软件对图2(a)所示电路进行仿真。仿真模型中高压系统为10kV，低压系统为400V，线性负荷电阻为1.5Ω，非线性整流负荷电阻为2Ω，主电网系统(包括主电网、传统变压器)的等效电抗为0.18mH。

图4 PET与主电网系统的等效阻抗图Fig.4 Equivalent impedance of PET and main grid (MG)

图5(a)和图5(b)分别为采用固态开关与传统变压器时微电网与主电网高、低压侧电压电流波形。对比电压波形可以发现，由于主电网等效阻抗与传统变压器等效电感的存在，低压侧电压发生畸变，THD为8.2%。对比电流波形可以发现系统高、低压侧电流波形形状基本一致，说明传统变压器不能隔离配电网高、低压侧间的谐波电流。

图5 采用固态开关的微电网电压电流波形图Fig.5 Voltage and current waveforms of microgrid with SSW

图6(a)和图6(b)分别为PET替代传统变压器后高、低压侧电压电流波形。对比电流波形可以发现高、低压侧电流波形不一致， PET实现了高、低压之间的谐波电流隔离。对比图5(b)与图6(b)的电压波形可发现，传统变压器低压侧波形(THD为8.2%)优于PET低压侧的电压波形(THD为15.7%)。

图6 采用PET时微电网电压电流波形图Fig.6 Voltage and current waveforms of microgrid with PET

由以上分析可知，当PET输出侧不采取任何电压质量调节措施且没有其他电压质量调节设备配合时，PET存在劣化PCC点电压质量的可能，而这一问题以往没有得到足够的重视。

3 电力电子变压器电压质量控制

3.1 PET电压质量调节本质分析

配电网非线性谐波负荷可以分为电压源型谐波负荷与电流源型谐波负荷两种。图7为PET同时接线性负荷、电压源型非线性负荷和电流源型非线性负荷的系统等效图。其中，谐波电压源的物理模型可以简化为理想谐波电压源VSh与等效并联阻抗ZVh串联而成；ISh表示谐波电流源中的谐波成分；ZPET表示谐波等效输出阻抗；ZL表示接在PCC点上的线性负载。

图7 含非线性谐波负荷的系统等效图Fig.7 Equivalent circuit with non-linear load

由图7可得：

(5)

(6)

(7)

(8)

I1=I2+I3+I4-ISh

(9)

综合式(5)～式(9)可得：

(10)

式中

YPET(s)=1/ZPET(s)，YL=1/ZL

Y∑=YPET+YVh+YCh+YL

YVh=1/ZVh，YCh=1/ZCh

此时PET输出级参考电压Uref为不含谐波的正弦电压，PCC点电压畸变的原因主要来源于式(10)第2项和第3项的影响。因此VSh与ISh前面系数的大小直接决定了PCC点电压畸变的程度。谐波源的阻抗一般较小，因此其导纳一般很大，当负载阻抗ZL不变时，可通过减小PET谐波阻抗，即增大YPET的方法来减小谐波源对VPCC点电压造成的影响。考虑到PET输出级可用于电压质量调节的容量存在限制，实际治理时满足Yoh>(YL+YVh)就可明显降低VPCC点电压畸变率。

综合分析PET面对谐波电压源负荷与谐波电流源负荷时的电路特性可以发现，改变PET输出级谐波阻抗可调节PCC点电压质量。现有文献已对虚拟阻抗法开展了大量研究，用于解决并联环流与谐振等问题，同时虚拟阻抗法在解决分布式微电源并联系统线路阻抗差异带来的谐波功率不均分问题[23,24]中得到了一定的关注。但将虚拟阻抗法用于PET还需要规避其对负荷阻抗特性敏感等问题，并且相关控制方法的选择需要满足PET实际采样与运行特点。

3.2 PET输出级电压质量控制策略

综合考虑PET实际采样与容量的诸多限制，本文提出了一种PET直接电压控制与虚拟阻抗控制结合的策略，如图8所示。

本文所提控制策略包括电压控制环节和虚拟阻抗环节两部分。本文控制策略的提出还充分考虑以下三个问题：

(1)电压指令基准的选择问题：电压包括幅值与相位两个重要组成部分，电压指令基准的选择直接关系到调节效果和可用容量的使用效率。

图8 PET输出级直接电压控制框图Fig.8 Direct voltage control sketch of output-stage

(2)电压控制器选择问题：目前PI控制器使用较多，其具有实现简单、通用性强等优点，但PI控制器对交流信号的响应特性差，参数设计敏感；若使用PI控制器对直流信号进行控制需多次信号提取、直流滤波与d-q转换，这将占用数字信号处理器(Digital Signal Processor，DSP)大量的计算时间。

(3)补偿容量受限问题：实际运行中，保障基波功率供给是PET运行的前提，因此进行供电电压质量控制时考虑PET容量限制是不可回避的问题。

3.2.1 电压控制环节分析

针对问题1和问题2，PET电压指令采用PCC点采样电压，直接电压反馈降低了控制系统对负载阻抗变化的敏感度，有利于动态跟随系统变化而做出反应。电压控制器采用PR谐振控制器而非PI控制器，PR控制器的优势在于适用于交流信号的直接控制，可直接将PCC点电压作为控制系统的输入；其次，PR控制器在谐振频率附近具有较大增益，在非谐振频率处响应差，可实现基波环节和各个谐波环节的解耦而无需考虑谐波对基波控制带来的影响；最后，PR控制器的谐振特性使得其能够对非谐振点外的信号进行滤波，在进行多次谐波综合治理时无需多次d-q变换来提取谐波电压，简化了控制系统结构与数字信号处理器的计算量。

(11)

式中

其中，Uout_h(k-1)为k-1时刻PET输出电压中的谐波分量；Mh为谐波电压幅值的调节系数，可以通过调整补偿系数对谐波电压指令进行动态调整。

采用PR控制器的PET输出电压表达式为：

(12)

式中，GU(s)为电压外环多谐振控制器的传递函数；GI(s)为电流内环比例增益函数；KPWM为PET控制器调制增益。GU(s)的表达式为：

(13)

式中，KPV为比例增益系数；Krh为谐振控制器增益系数；ωch为截止频率；ω0为基波频率。

3.2.2 考虑容量限制的虚拟阻抗控制环节分析

在仅采用电压外环的情况下可以实现对PCC点供电电压质量的有效控制，但是PET的主要任务依然是保证基波能量的供给，因此在进行供电电压质量控制时考虑PET的可用补偿容量是不可回避的问题，即问题3如何解决。基于此，本文提出了通过引入虚拟阻抗环节来动态跟随PET实际剩余容量调节供电电压质量的新方法。

对式(12)分析可以发现，改变iout在控制环节的正向增益是改变PET等效阻抗的可行方法。基于这一机理，本文在直接电压控制的基础上提出采用虚拟阻抗环节调节PET等效输出阻抗，其控制部分如图8所示。PET输出电流iout的正向增益为GIR，表达式为：

(14)

(15)

此时PET输出电压调整为：

Uout(s)=GU(s)Uref-Zof(s)iof-(1-k)Zoh(s)ioh

(16)

式中，k为补偿系数。补偿系数的引入可以实现对供电电压质量进行动态治理。当k=1时，谐波阻抗为0，此时为全补偿；当k=0时，系统处于无补偿状态。随着k值的增加，谐波阻抗不断减小，PCC点电压得到改善；随着k值的减小，谐波阻抗不断增大，PCC点电压质量将逐渐下降。

补偿系数k的取值方法如式(17)所示：

k=k*-m(S0-S)

(17)

式中，S0为PET可用补偿容量；S为实际PET的谐波输出容量。S0和S的表达式为：

(18)

(19)

Sout=Uout_rmsIout_rms

(20)

式中，SN为PET输出级的额定容量；Sout为PET输出级运行的视在功率，包含基波视在功率与谐波视在功率；Uout_rms为输出电压有效值；Iout_rms为输出电流有效值。

式(17)中，k*为当S0=S时的补偿系数，取值范围为[0,1]。m为谐波电压改善率，其表达式为：

m=(kmax-k*)/S0

(21)

当S=0时kmax=1。由式(17)可以发现，PET输出级基波功率较少时，补偿系数k可取较大的值，此时对PCC点电压调节能力更强。相反，当PET基波功率交换较多时，补偿系数k的取值范围将缩小，PCC点电压质量的调节能力下降。

通过虚拟阻抗环节与补偿系数的综合作用，可实现根据PET运行状态动态调节其供电电压质量。

3.3 响应特性分析

由控制器传递函数可以得到PET的电压响应传递函数与阻抗传递函数分别为：

(22)

(23)

为了凸显本文所提控制策略的有效性，针对式(22)和式(23)分别对比分析了电压环采用PI控制与PR控制的响应特性，以及PET输出级的阻抗特性，结果如图9和图10所示。

图9 电压指令信号响应图

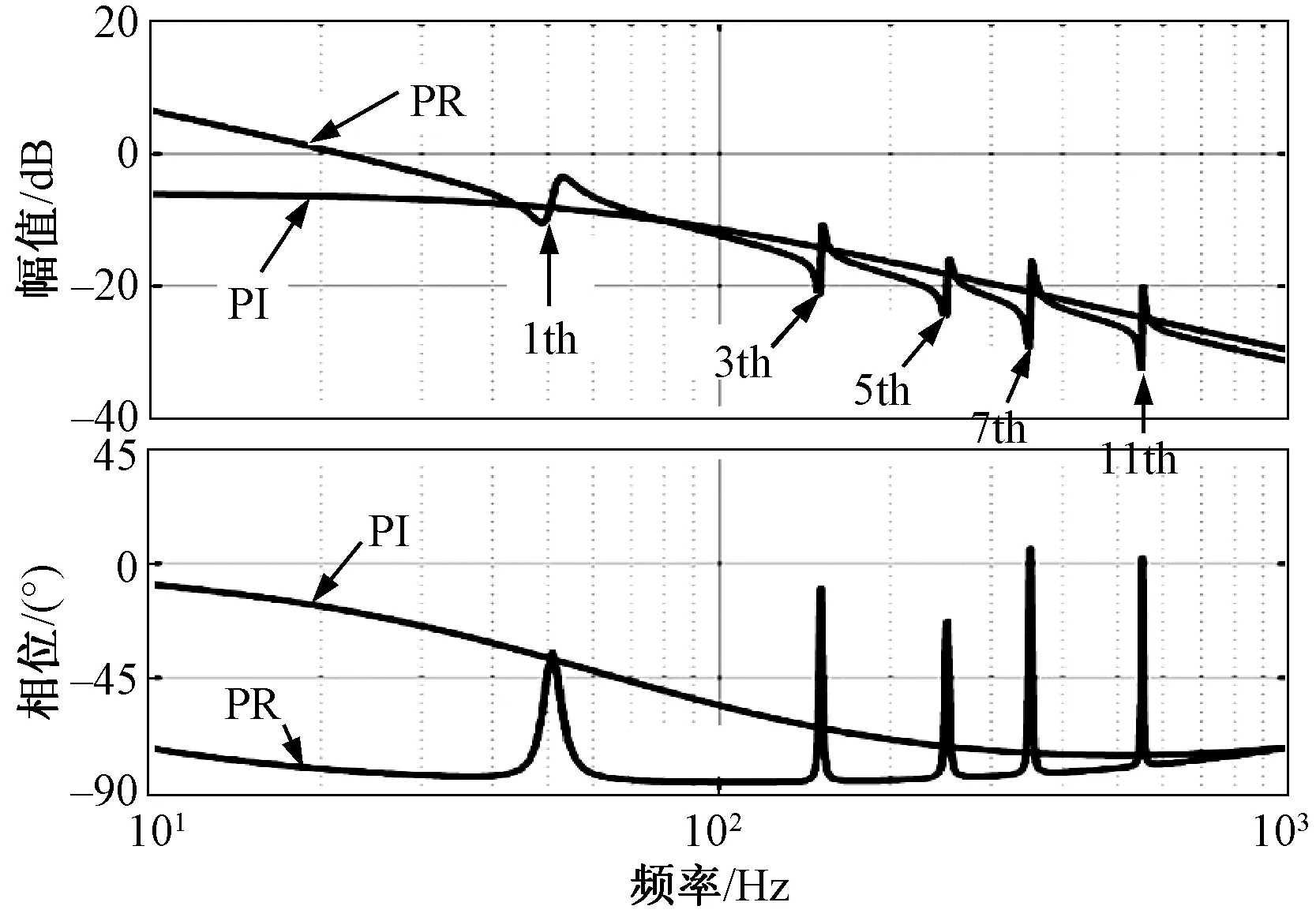
图10 PET输出级等效阻抗Fig.10 Equivalent impedance of output-stage

图9为电压环增益函数GU(s)采用PI控制和PR控制时指令电压的响应特性曲线。可见，采用PR控制器时在基波和各次谐波频率处增益接近0dB与0°，表明PR控制器不仅能实现基波指令的准确跟踪，还能实现特定谐波频率处指令的准确跟踪。采用PI控制时，其各频次处的幅频响应特性显然比PR控制差。因此，采用PR控制的指令电压响应特性优于PI控制的响应特性。

图10为采用PI控制与PR控制时的PET等效谐波阻抗。可见，PR控制下的等效谐波阻抗相比PI控制小，且特定谐波处有非常大的差距。因此从等效阻抗值上亦可以看出直接电压PR控制具有更好的谐波控制能力。

4 实验研究

为了验证所提PET输出级电压质量控制策略，对图2的供电系统进行实验验证。PET输出侧的系统参数如表1所示。PET输出级的控制器采用TI公司的DSP TMS320F2812，采样频率与IGBT的开关频率均为10kHz。

表1 PET输出侧参数Tab.1 Parameters of output-stage

(1)工况1(无补偿)

图11为无补偿(补偿系数k=0)时的PET输出侧电压电流波形图。由图11(b)可以看出，当PET输出级不进行任何电压质量调节时，输出侧PCC点电压波形畸变较大，与第2节的理论分析一致。此时电压总畸变率约为17.5%，相比第2节仿真中的15.7%的畸变率略有增大，这与实际控制器为离散型控制器存在一定的关系。

图11 无补偿时电压电流波形Fig.11 Voltage and current waveforms without compensation

(2)工况2(全补偿)

图12为谐波补偿率为100%(补偿系数k=1)时的PET输出侧电压电流波形图。对比图12(b)和图11(b)可以看出，全补偿时PET输出侧PCC点电压相比无补偿时波形整体更加平滑，电压畸变得到了明显改善。在图12(b)中圆圈等处可以看出依然含有高频谐波与极少量的低频谐波，但此时电压畸变率已由无补偿时的17.5%降低到3.2%左右，治理效果较明显。从整体的治理效果来看，本文提出的方法能够有效改善PCC点电压质量，实验证明了所提方法的有效性。

图12 全补偿时电压电流波形Fig.12 Voltage and current waveforms with full compensation

5 结论

含PET的微电网电能质量与其他类型的微电网存在一定差异，本文对比分析了两种类型微电网的电能质量差异，并针对PET的特点提出了一种适用于PET的电压质量控制策略。本文的相关研究可得到以下结论：

(1)PET替代传统变压器或固态开关后，若不进行电压质量调节则易受微电网内部非线性负荷影响，从而导致PCC点电压质量劣化，因此对PET的电压质量控制策略开展研究具有重要意义。

(2)所提PET电压控制策略具备全局管理PCC点电压质量的能力，可以兼顾抑制电流型谐波负荷与电压型谐波负荷。

(3)所提出的基于虚拟阻抗控制的电压控制策略考虑了PET补偿容量限制，控制方式灵活可控且易于实现，符合PET实际应用的需求；同时，所提控制策略具有较好的可移植性，可适用于其他电压源型变流器或电流源型变流器。

参考文献(References)：

[1] 严太山, 程浩忠, 曾平良, 等 (Yan Taishan, Cheng Haozhong, Zeng Pingliang, et al.). 能源互联网体系架构及关键技术 (System architecture and key technologies of Energy Internet) [J]. 电网技术 (Power System Technology), 2016, 40 (1):105-113.

[2] Dujic D, Zhao C, Mester A, et al. Power electronic traction transformer - Low voltage prototype [J]. IEEE Transactions on Power Electronics, 2013, 28(12): 5522-5534．

[3] 刘海波, 毛承雄, 陆继明, 等 (Liu Haibo, Mao Chengxiong, Lu Jiming, et al.). 配电系统电子电力变压器非线性控制 (Nonlinear control of electronic power transformer for distribution systems) [J]. 中国电机工程学报 (Proceedings of the CSEE), 2009, 29(27): 1-8.

[4] 凌晨, 葛宝明, 毕大强 (Ling Chen, Ge Baoming, Bi Daqiang). 配电网中的电力电子变压器研究 (A power electronic transformer applied to distribution system) [J]. 电力系统保护与控制 (Power System Protection and Control), 2012, 40(2): 34-39.

[5] 张明锐, 刘金辉, 金鑫 (Zhang Mingrui, Liu Jinhui, Jin Xin)．应用于智能微电网的 SVPWM 固态变压器研究 (Research on the SVPWM solid state transformer applied in smart micro-grid) [J]. 电工技术学报(Transactions of China Electrotechnical Society), 2012, 27(1): 90-97.

[6] 刘闯, 支月媚 (Liu Chuang，Zhi Yuemei). 混合级联式电力电子变压器拓扑结构及控制策略 (Hybrid cascaded power electronics transformer topology and control scheme) [J]. 电网技术 (Power System Technology), 2017, 41(2): 596-603.

[7] Fan H, Li H. High-frequency transformer isolated bidirectional DC-DC converter modules with high efficiency over wide load range for 20 kVA solid-state transformer[J]. IEEE Transactions on Power Electronics, 2011, 26(12): 3599-3608.

[8] 王杉杉, 王玉斌, 林意斐, 等 (Wang Shanshan, Wang Yubin, Lin Yifei, et al.). 级联型电力电子变压器电压与功率均衡控制方法 (Voltage and power balance control for cascaded multilevel converter based power electronic transformer) [J]. 电工技术学报 (Transactions of China Electrotechnical Society), 2016, 31 (22): 92-99.

[9] 李响, 郝瑞祥, 游小杰, 等 (Li Xiang, Hao Ruixiang, You Xiaojie, et al.). 一种级联电力电子变压器直流电压平衡控制策略 (A DC voltage balance control strategy for the cascaded power electronic transformer) [J]. 电工技术学报 (Transactions of China Electrotechnical Society), 2017, 32(2): 238-245．

[10] Fan B, Li Y, Wang K, et al. Hierarchical system design and control of an MMC-based power electronic transformer[J]. IEEE Transactions on Industrial Informatics, 2017, 13(1): 238-247.

[11] 高范强, 李子欣, 徐飞, 等 (Gao Fanqiang，Li Zixin，Xu Fei, et al.). 一种高频链模块化电力电子变压器 (Power electronic transformer based on modular converter with high-frequency link)[J]. 电工电能新技术 (Advanced Technology of Electrical Engineering and Energy), 2017, 36(5): 51-58.

[12] 兰征，涂春鸣，肖凡，等 (Lan Zheng，Tu Chunming，Xiao Fan，et al.). 电力电子变压器对交直流混合微电网功率控制的研究 (The power control of power electronic transformer in hybrid AC-DC microgrid) [J]. 电工技术学报 (Transactions of China Electrotechnical Society), 2015, 30(23): 50-57.

[13] Yu X, She X, Ni X, et al. System integration and hierarchical power management strategy for a solid-state transformer interfaced microgrid system [J]. IEEE Transactions on Power Electronics, 2014, 29(8): 4414-4425.

[14] Shi J, Gou W, Yuan H, et al. Research on voltage and power balance control for three-phase cascaded modular solid-state transformer[J]. IEEE Transactions on Power Electronics, 2011, 26(4): 1154-1166.

[15] Zhao T, Wang G, Bhattacharya S, et al. Voltage and power balance control for a cascaded H-bridge converter-based solid-state transformer [J]. IEEE Transactions on Power Electronics, 2013, 28(4): 1523-1532.

[16] Chen Qifang, Liu Nian, Hu Cungang, et al. Autonomous energy management strategy for solid-state transformer to integrate PV-assisted EV charging station participating in ancillary service[J]. IEEE Transactions on Industrial Informatics, 2017, 13(1): 258-269.

[17] 金一丁, 宋强, 刘文华 (Jin Yiding， Song Qiang， Liu Wenhua). 基于公共直流母线的链式可拓展电池储能系统及控制 (Control and analysis of extensible cascaded battery energy storage system based on a common DC bus) [J]．电力系统自动化 (Automation of Electric Power Systems), 2010, 34(15): 66-70.

[18] García P, Saeed S, Navarro-Rodríguez, et al. Switching frequency optimization for a solid state transformer with energy storage capabilities[A]. 2016 IEEE Energy Conversion Congress and Exposition (ECCE) [C]. Milwaukee, WI, USA， 2016.1-8.

[19] Chen Y, Guerrero J M, Shuai Z, et al. Fast reactive power sharing, circulating current and resonance suppression for parallel inverters using resistive capacitive output impedance[J]. IEEE Transactions on Power Electronics, 2016, 31(8): 5524-5537.

[20] Sreekumar P, Khadkikar V. Direct control of the inverter impedance to achieve controllable harmonic sharing in the islanded microgrid[J]. IEEE Transactions on Industrial Electronics, 2017, 64(1): 827-837.

[21] Hamzeh M, Karimi H, Mokhtari H. Harmonic and negative-sequence current control in an islanded multi-bus MV microgrid[J]. IEEE Transactions on Smart Grid, 2014, 5(1): 167-176.

[22] Zhong Q C, Blaabjerg F, Guerrero J M, et al. Improving the voltage quality of an inverter via by-passing the harmonic current components[A]. IEEE Energy Conversion Congress and Exposition (ECCE) [C]. Raleigh, North Carolina, USA， 2012. 4037-4041.

[23] Hassan Moussa, Ahmed Shahin, Jean-Philippe Martin, et al. Harmonic power sharing with voltage distortion compensation of droop controlled islanded microgrids[J/OL]. IEEE Transactions on Smart Grid. DOI:10.1109/TSG.2017.2687058.

[24] Zhong Q C. Harmonic droop controller to reduce the voltage harmonics of inverters[J]. IEEE Transactions on Industrial Electronics, 2013, 60(3):936-945.

[25] Zhao Biao, Song Qiang, Liu Wenhua. A practical solution of high frequency link bidirectional solid-state transformer based on advanced components in hybrid microgrid[J]. IEEE Transactions on Industrial Electronics, 2015, 62(7): 4587-4597.

[26] She X, Huang A Q, Ni X. Current sensorless power balance strategy for DC/DC converters in a cascaded multilevel converter based solid state transformer[J]. IEEE Transactions on Power Electronics, 2014, 29(1): 17-22.

[27] Wang Dan, Tian Jie, Mao Chengxiong, et al. A 10-kV/400-V 500-kVA electronic power transformer[J]. IEEE Transactions on Industrial Electronics, 2016, 63(11): 6653-6663.