一个新的未知参数超混沌系统的自适应同步

于海东，刘 爽，岳立娟

(东北师范大学物理学院，吉林 长春 130024)

混沌是非线性动力学系统所特有的一种复杂运动形式，是自然界普遍存在的复杂现象.由于混沌的同步与控制在物理、通信、信息科学、医学等领域的巨大应用潜力和发展前景，得到了广泛关注.1990年，L.M.Pecora等[1]提出了混沌同步的方法并在电路中得以实现.自此以后，一些学者相继设计出了各种同步方法，例如耦合同步、反馈同步、驱动响应同步、变结构同步、驱动参量法等.[2-7]近年来，基于状态观测器的混沌同步法[8]、广义同步法[9]、基于神经网络的同步法[10]、基于 T-S模糊模型的同步法[11]等广泛应用在各种混沌系统中.然而，这些方法讨论的几乎都是确定的或参数已知的混沌系统，但在实际应用中，混沌系统的参数常常是未知或不确定的.因此，要在参数未知的不确定混沌系统下实现混沌同步对实际的混沌系统至关重要.近年来国内外一些学者对此做了深入的研究，如J.H.Park[12]提出了参数不确定 Rössler 系统的自适应同步法；陈士华等[13]基于参数辨识方法研究了超混沌Rössler 系统的自适应同步；王燕舞等[14]完成了完全不确定Chen 系统的自适应同步；E.M.Elabbasy等[15]分析了参数不确定 Lǜ 系统的自适应同步.当系统中某些参数未知时，混沌系统的敏感性将造成系统状态极大的差异.自Hilbert提出隐藏领域以来，研究发现具有隐藏吸引子的系统对初值及参数极其敏感，但对其进行同步与控制的研究较少.

本文在Sprott B系统的基础上通过增加非线性项构造了一个新的五维超混沌系统，该系统只具有一个参数.对系统进行动力学特性分析，发现新系统具有隐藏吸引子的特性，基于自适应方法对该系统进行同步研究，根据 Lyapunov稳定性理论，得到同步的充分条件，并设计出参数辨识和系统同步的自适应控制律.理论分析与数值模拟证明了该方法的有效性.

1 一个新的五维超混沌系统

在Sprott B系统的基础上通过增加非线性项构造出一个新的五维超混沌系统：

(1)

其中：a是新系统参数；x1，x2，x3，x4，x5是系统的状态变量.当参数a=0.2时，初值为(x1(0)，x2(0)，x3(0)，x4(0)，x5(0))=(0.05，0.05，0.05，0.05，0.05)时，计算系统(1)的Lyapunov指数：λ1=0.386 161，λ2=0.040 577，λ3=0，λ4=-0.030 146，λ5=-0.415 503，则Lyapunov指数为

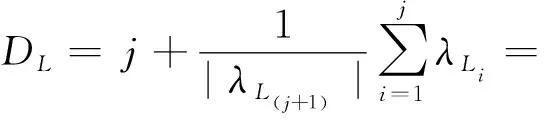
(2)

新的五维系统(1)为超混沌系统，其吸引子如图1所示.

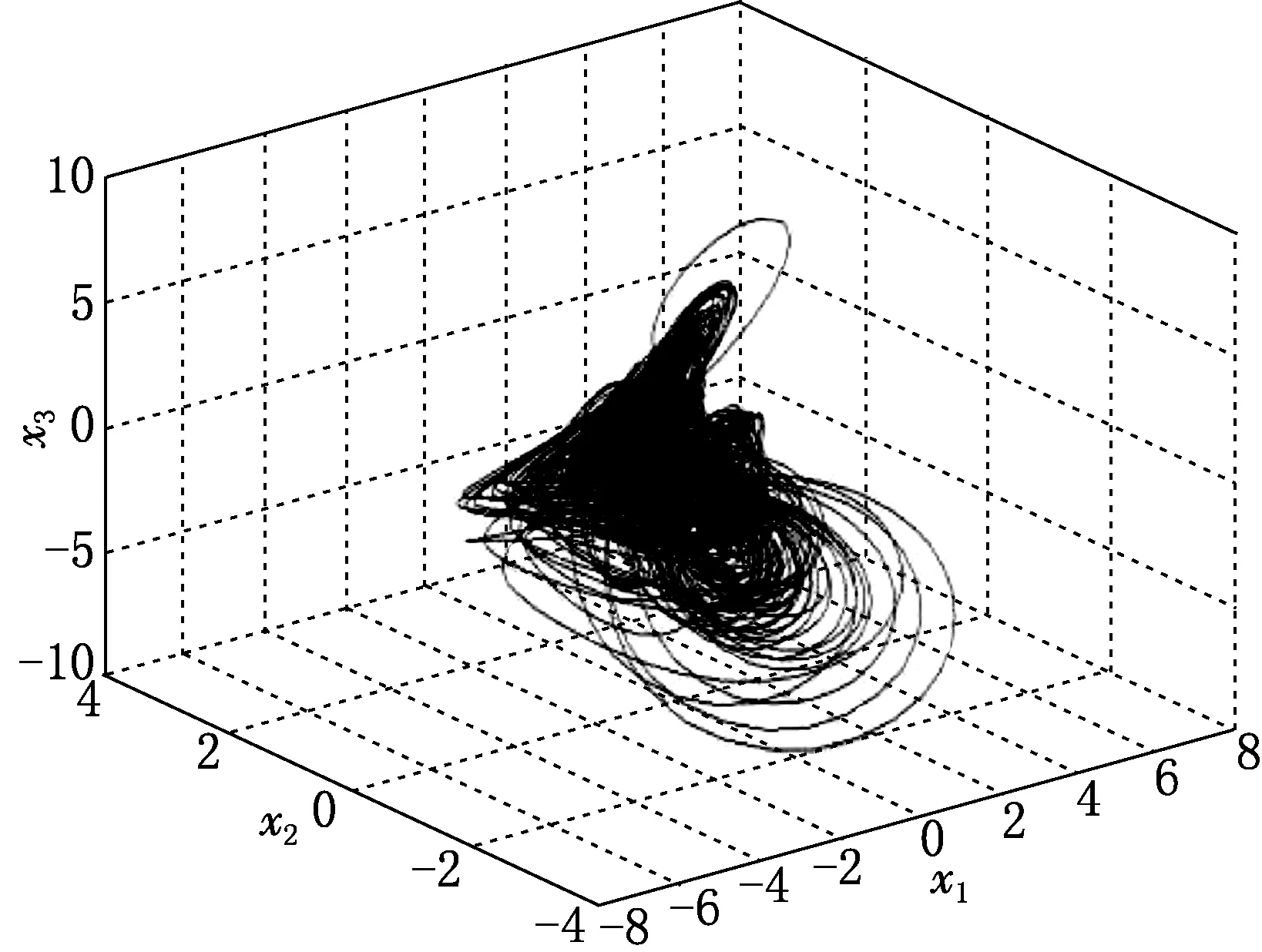
图1 新超混沌系统的吸引子

对于系统(1)有

(3)

所以系统(1)是耗散的，并以指数dV/dt=e-t收敛，即随着t→∞时，包含系统轨线的每一个体积元都以e-t收缩到0.所有的系统轨线将会被限制在一个体积为零的极限子集上，且它的渐进动力学行为被固定在一个吸引子上，也进一步说明了吸引子的存在.

新系统(1)只具有一个参数a，随a变化的Lyapunov指数谱及分岔图见图2，从图2可以看出a∈(-0.2，0.6)，系统(1)处于超混沌状态.

(a)Lyapunov指数谱

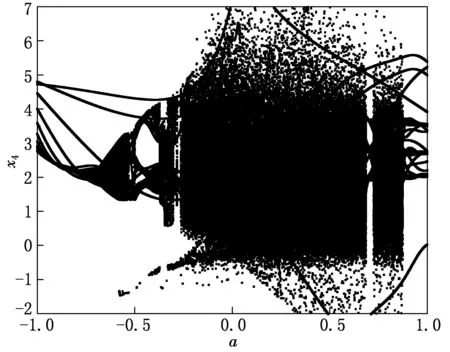
(b)分岔图

图2随a变化的Lyapunov指数谱和分岔图

由系统(1)得到平衡点方程为：

(4)

可见系统(4)没有平衡点.通过D.David等[16]提出一个系统如果没有平衡点或者有且只有一个稳定的平衡点，则具有隐藏吸引子，这样的系统对初值及参数的改变极为敏感.系统(1)将初值x1(0)及参数a只改变1%得到x1时域图如图3所示，可见系统(1)具有较好的初值敏感性和参数敏感性.

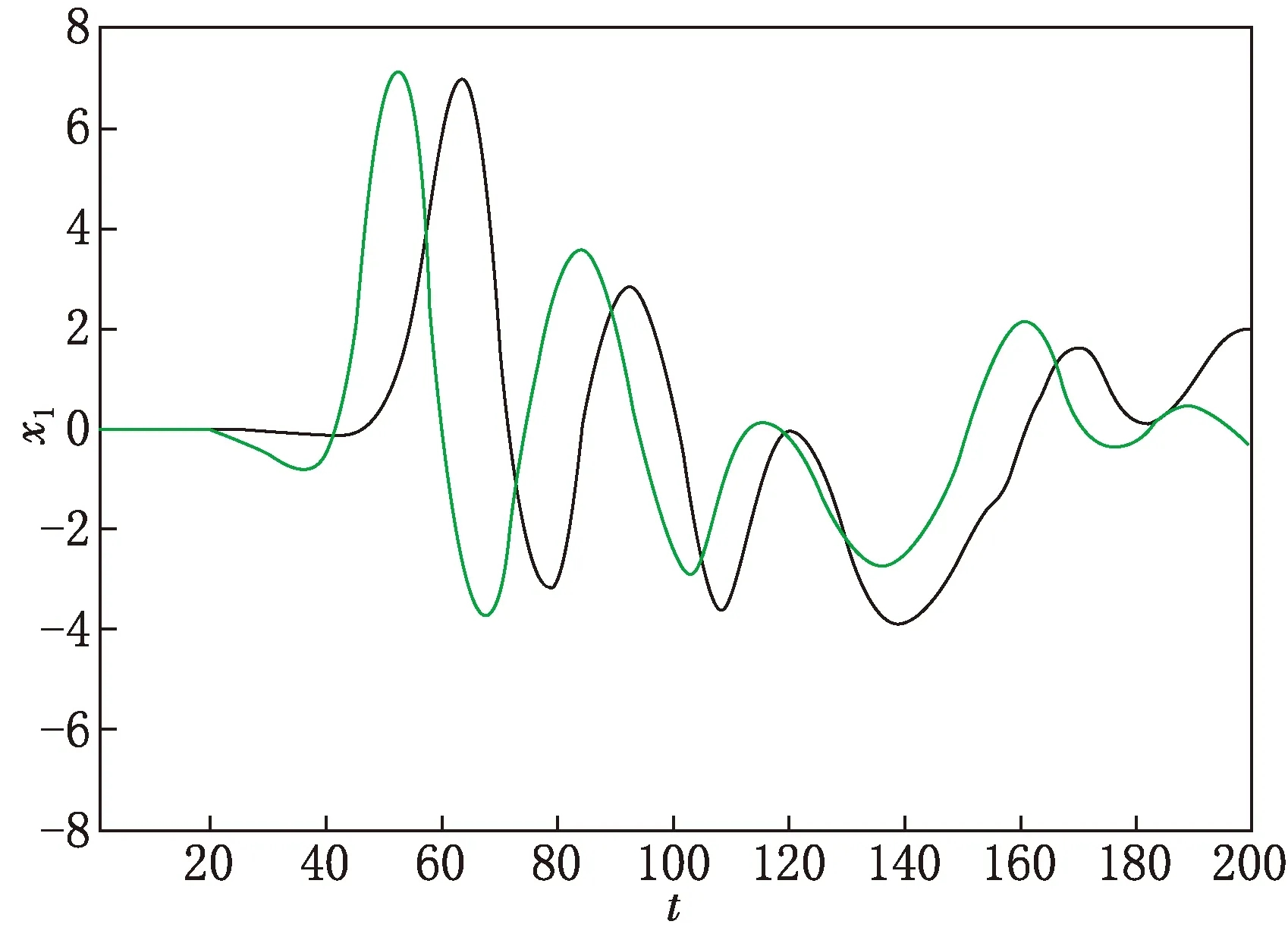
(a)不同初值下x1的时域图

2 自适应同步控制器的设计方案

驱动系统为

(5)

响应系统为

(6)

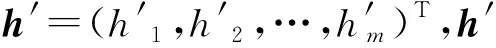
控制器误差系统为

(7)

控制器参数误差为：

eh=h′-h；
Ahx=F(x)h；
Ah′y=F(y)h′.

(8)

则Ah′y-Ahx=F(y)h′-F(x)h=Ah′e+F(x)eh，则F(x)和F(y)是关于系统状态变量x，y的l×m矩阵.

定理如果选取控制器

u=f(x)-f(y)-ke，

(9)

其中k=diag(k1，k2，…，kn).

参数自适应律为：

(10)

则驱动系统与响应系统全局渐进同步.

证明误差系统为

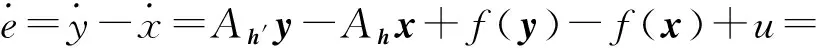
(11)

选取Lyapunov函数为

(12)

对V求导并利用(10)式可得

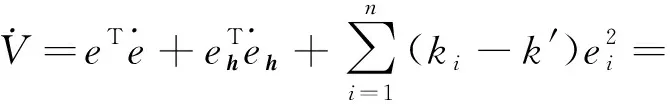
其中λmin(P)为正定矩阵P的最小特征值，所以有e∈L，根据Barbalat引理可得

即系统(5)和系统(6)全局渐进同步.

3 参数未知新超混沌系统的自适应同步

设系统(1)为驱动系统，响应系统为：

(13)

定义误差为e=y-x，则误差系统为：

(14)

根据自适应控制方法，我们可以设计控制器为：

(15)

参数自适应为：

(16)

构造Lyapunov函数为

对V进行求导，可得

由于混沌系统具有初值敏感性，所以在开始时混沌吸引子在不同的轨道运动，但由于混沌系统具有有界性，所有的状态变量经过一段时间后都会到达吸引子集，即一定存在一个正实数L使得

|xi|≤L<∞(i=1，2，3，4，5).

因此

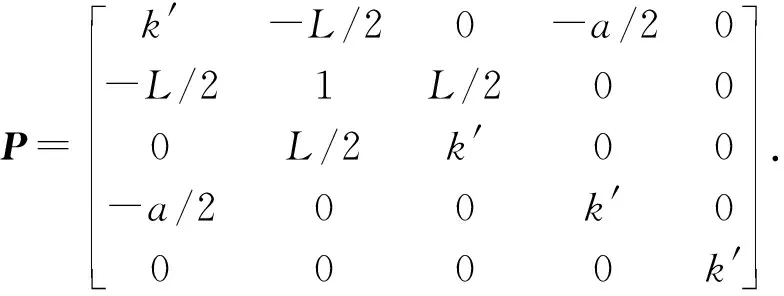
需选取适当k′值，使

通过数值仿真得到如下结果：ei(i=1，2，3，4，5)随时间t变化图像见图4，参数a的辨识曲线见图5，参数自适应律ki(i=1，2，3，4，5)收敛曲线见图6，实验结果表明ki随着时间演化趋向一个常数，两系统很快实现同步.

图4 ei(i=1，2，3，4，5)随时间t变化图像

图5 参数a辨识曲线

图6 参数自适应律ki(i=1，2，3，4)收敛曲线

4 总结

本文在Sprott B系统的基础上构造了新的五维超混沌系统，该系统只具有一个参数.经过对其动力学特性分析，发现其具有隐藏吸引子这一特性，通过对初值及参数进行微小的改变，观察时域图具有较明显的变化，证明了具有隐藏吸引子的系统对初值及参数极其敏感.基于 Lyapunov 稳定性理论，利用自适应同步方法，对参数不确定的具有隐藏特性新的五维超混沌系统进行同步研究，设计和构造自适应同步控制器及自适应律.仿真结果表明，同步时间较短，同步效果较好.设计的控制器简单且易于选取，适用范围广.

[参 考 文 献]

[1] PECORA L M，CARROLL T.L A circuit for studying the synchronization of chaotic systems[J].International Joural of Bifurcation and Chaos，1992，2(3)：659-667.

[2] 方锦清.非线性系统中的混沌的控制与同步及其应用前景[J].物理学进展，1996，16(1)：1-3.

[3] 王光瑞，于熙龄，陈式刚.混沌的控制、同步与利用[M].北京：国防工业出版社，2001：334-395.

[4] 张化光，王智良，黄伟.混沌系统的控制理论[M].沈阳：东北大学出版社，2003：115-140.

[5] WINFUL H G，RAHMAN L.Synchronized chaos and spatiotemporal chaos in arrays of coupled lasers[J].Phys Rev Lett，1990，65：1575-1578.

[6] SURAWARA T，TACHIKAWA M，TSUKAMOTO T，et al.Observation of synchronization in laser chaos[J].Phys Rev Lett，1994，65：3602-3604.

[7] ROY R，THORNBURG K S.Experimental synchronization of chaotic lasers[J].Phys Rev Lett，1995，72：2009-2012.

[8] PYRAGAS K.Experimental control of chaos by delayed self-controlling feedback[J].Physics Letters A，1993，180：99-102.

[9] HUBERMAN A.Dynamics of adaptive systems[J].IEEE Transactions on CAS，1990，37：547-550.

[10] 兰祝刚，彭巍，丘水生.混沌同步方法的研究[J].通信技术，2001，5(1)：28-31.

[11] YANG T，CHUA L O.Impulsive stabilization for control and synchronization of chaotic systems：Theory and application to secure communication[J].IEEE Transactions on CAS，1997，44(10)：976-988.

[12] PARK J H.On synchronization of unfied chaotic systems via nonlinear control[J].Chaos，Solitons Fract，2005，25：333-337.

[13] 陈士华，谢进，陆君安，等.Rössler系统的追踪控制与同步[J].物理学报，2004，51(4)：749-752.

[14] 王燕舞，关治洪，王华，等.自适应控制实现陈氏系统的完全控制[J].华中科技大学学报(自然科学版)，2002，30(12)：49-51.

[15] ELABBASY E M，AGIZA H N.Synchronization of modified Chen system[J].Chaos，Solitons Fract，2004，21：657-662.

[16] DAVID D，SAJAD J，TOMASZ K.Hidden attractors in dynamical systems[J].Physics Reports，2016，637：1-50.