一类具有隔离效应的随机SIS传染病系统的动力学行为

赵 春 园

(1.东北师范大学环境学院，吉林 长春130024； 2.吉林交通职业技术学院管理工程学院，吉林 长春 130021)

1 预备知识

研究流行病发生机理、传染规律及防治策略对疾病的预防与控制具有重要意义.随着科学的发展，学者们在不断利用科学知识通过建立模拟传染病传播规律的数学模型，将疾病传播规律与特点公式化.最近，在随机干扰的作用下，研究某种疾病消失及流行的可能性已经成为流行病学中的一个研究主题.[1-4]隔离效应也已经成为消除传染病的一个重要策略，许多学者研究了具有隔离效应的传染病模型.[5-8]在许多现有的模型中，双线性发生率已被频繁使用.Gray等[9]研究具有双线性发生率的随机SIS传染病模型时，通过控制随机噪声强度得到了该系统中感染者种群灭绝及持久的充分性条件.然而，当易感者个体的数量较大时，在一定时间内易感者个体之间存在着感染性接触，即存在着饱和效应.这些事实表明，饱和发生率对许多情形来讲都更为合理.[10-13]基于这样的考虑，本文主要考虑具有隔离效应和饱和发生率的随机SIS传染病模型

(1)

2 正解的存在唯一性

研究随机传染病模型的动力学行为，首先要考虑模型是否存在全局正解.众所周知，存在唯一性定理一般要求系统满足局部Lipschitz条件和线性增长条件.然而，系统(1)的系数只是满足局部Lipschitz条件，线性增长条件并不满足，所以有可能会在有限时间内爆破.本文主要利用文献[10]中Lyapunov分析方法证明随机微分方程(1)存在唯一的全局正解.

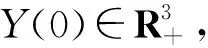
τm=inf{t∈[0，τe)|S(t)∉(1/m，m)或者I(t)∉(1/m，m)或者Q(t)∉(1/m，m)}，

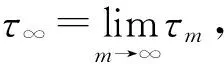
假设上述结论不成立，那么存在常数T和∈(0，1)，使得P{τ∞≤T}>，存在整数m1≥m0，对于m≥m1，满足

P{τm≤T}≥.

(2)

由伊藤公式可得

(3)

其中

对(3)式两边积分，取期望得

EV(S(τk∧T)，I(τk∧T)，Q(τk∧T))≤
V(S(0)，I(0)，Q(0))+KE(τk∧T)≤
V(S(0)，I(0)，Q(0))+KT.

(4)

对于k≥k1，令Ωk={τk≤T}，则P(Ωk)≥ε.由于对每一个ω∈Ωk，在S(τk，ω)，I(τk，ω)和V(τk，ω)中至少有一个等于k或1/k，所以V(S(τk，ω)，I(τk，ω)，Q(τk，ω))不小于

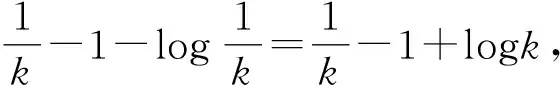
于是

由(2)和(4)式，

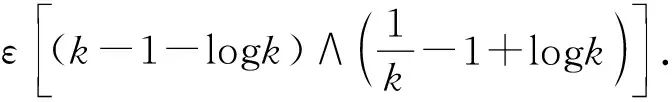
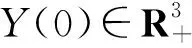
3 无病平衡点P0附近的渐近性行为

研究传染病数学模型时，疾病何时流行、何时消亡一直是关键问题.对于确定性传染病模型，许多学者通过研究传染病模型的无病平衡点和地方病平衡点的稳定性，来分析得到的疾病流行与灭绝的条件.然而，随机模型中一般不存在有病平衡点和无病平衡点，那么如何研究随机传染病模型的灭绝性和持久性便成为一个非常有意义的问题.本文主要探讨随机传染病系统(1)在无病平衡点处的渐近行为和遍历性，在一定程度上反映了疾病的消亡或流行，并关注白噪声对原确定系统的动力学行为的影响.

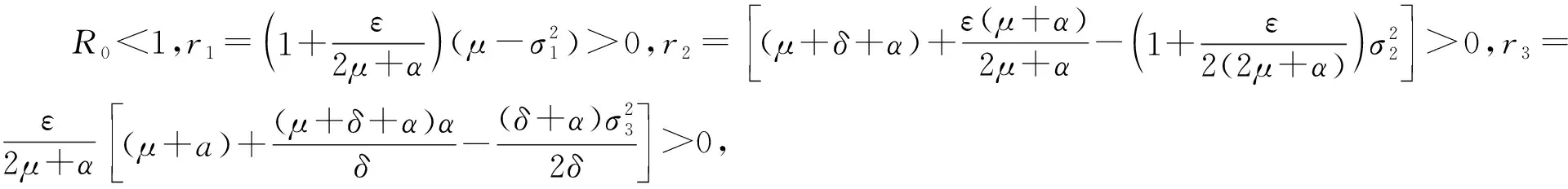
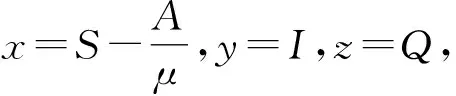
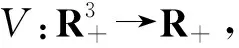
(5)

dV∶=lVdt+c1σ2ydB2(t)+(x+y)[σ1(x+A/μ)dB1(t)+σ2ydB2(t)]+
c2(x+y+z)[σ1(x+A/μ)dB1(t)+σ2ydB2(t)+σ3zdB3(t)]+c3σ3z2dB3(t).

由于R0<1，得到

注意到当

成立时，定理条件r1，r2，r3均大于0，从而

于是

因此

注1定理2表明，在R0<1和白噪声强度满足一定条件的情况下，系统(1)的解会在确定系统的无病平衡点附近震动，且震动强度和白噪声强度成正比.从生物学角度来解释，若传染病系统受到白噪声的影响越小，则系统(1)解的长时间行为会越接近于无病平衡点.

4 随机系统的遍历性行为

由于随机系统(1)的扩散项是非退化的，本文利用Hasminskii理论[4]给出系统(1)存在平稳分布，并且证明此平稳分布具有遍历性，从而表明疾病在定理条件下将会流行.

引理1[4]存在具有正则边界Γ的有界区域U⊂El，具有如下性质：

(1) 在U和它的一些邻域，扩散阵Λ(x)的最小特征值是非零的.

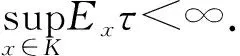
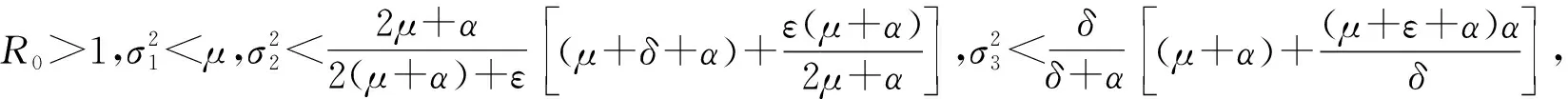
证明由于R0>1，则确定系统存在地方病平衡点P*，因此

(6)

利用伊藤公式求导有

其中

这里

由于

则椭圆

由引理1，随机系统(1)存在平稳分布μ(·)，且是遍历的.

5 总结

本文研究具有隔离效应和饱和发生率的随机SIS传染病模型的动力学行为.首先考虑具有任意正初值系统(1)全局正解的存在唯一性.然后根据基本再生数和白噪声强度，得到保证疾病持久和灭绝的充分条件.所得结果表明环境白噪声对疾病的持久性与灭绝性具有重要的影响.

当然一些有意义的问题值得进一步研究.一方面，可以提出一些更加符合实际情形并且复杂的模型，例如可以考虑时滞对系统(1)的影响.另一方面，本文所用到的方法也可以用来研究其他有意义的模型，如具有其他形式的非线性发生率的SIS(Susceptible Infective Susceptible)模型、SIRS(Susceptible Infective Removed Susceptible)模型和SEIRS(Susceptible Exposed Infective Susceptible)模型等.

[参 考 文 献]

[1] DALAL N，GREENHALGH D，MAO X R.A stochastic model of AIDS and condom use[J].J Math Anal Appl，2007，325: 36-53.

[2] JIANG D，JI C，SHI N，et al.The long time behavior of DI SIR epidemic model with stochastic perturbation[J].J Math Anal Appl，2010，372: 162-180.

[3] JIANG D，JI C，SHI N.Multigroup SIR epidemic model with stochastic perturbation[J].Physica A，2011，390: 1747-1762.

[4] YANG Q S，JIANG D Q，SHI N Z，et al.The ergodicity and extinction of stochastically perturbed SIR and SEIR epidemic models with saturated incidence[J].J Math Anal Appl，2012，388: 248-271.

[5] 杨俊仙，徐丽.一类具非线性发生率和时滞的SIQS传染病模型的全局稳定[J].山东大学学报(理学版)，2014，49(5):67-74.

[6] CHEN J J.Local stability and global stability of SIQS models for disease[J].Journal of Biomathematics，2004，19(1):57-64.

[7] PANG Y，HAN Y，LI W.The threshold of a stochastic SIQS epidemic model[J].Advances in Difference Equations，2014(1):1-15.

[8] 赵亚男，夏兰，王宇，等.具有随机扰动的SIQS传染病模型的渐进行为[J].吉林大学学报(理学版)，2013，51(4):161-167.

[9] GRAY A，GREENHALGH D，HU L，et al.A stochastic differential equation SIS epidemic model[J].SIAM J Appl Math，2011，71: 876-902.

[10] CAPASSO V，SERIO G.A generalization of the Kermack-Mckendrick deterministic epidemic model[J].Math Biosci，1978，42: 43-61.

[11] XIAO D，RUAN S.Global analysis of an epidemic model with nonmonotone incidence rate[J].Math Biosci，2007，208: 419-429.

[12] XU R，MA Z.Stability of a delayed SIRS epidemic model with a nonlinear incidence rate[J].Chaos Solitons and Fractals，2009，41: 2319-2325.

[13] HERBERT H，MA Z，LIAO S.Effects of quarantine in six endemic models for infectious diseases[J].Mathematical Biosciences，2002，180: 141-160.