半群Q(F，k)的极大正则子半带

阮海灯，游泰杰，赵 平

(贵州师范大学数学科学学院，贵州 贵阳 550001)

1 预备知识

设S是半群且a∈S.若a2=a，则称a是幂等元；若存在b∈S，使a=aba，则称a是正则元；若半群S的每个元是正则元，则称半群S是正则半群.设A是半群S的非空子集，若S中的每个元都可以表示成A中有限个元的乘积，则称A是S的生成集，记作S=〈A〉.若S由幂等元生成，则称S为一个半带.若半带S是正则半群，则称S为正则半带.

设S是正则半带.T是S的正则子半带(T⊂S)，且对S的任意正则子半带U，T⊂U⟹U=S，则称T为S的极大正则子半带.

设T(X)是X上的全变换半群且Y是X的非空子集.令T(X，Y)={α∈T(X)|Xα⊆Y}，则T(X，Y)是T(X)的子半群.1975年，Symon[1]研究了半群T(X，Y)的自同构.2009年，Sanwong和Sommane[2]证明了F(X，Y)={α∈T(X)|Xα⊆Yα⊆Y}是T(X，Y)的最大正则子半群，并且确定了T(X，Y)中的格林关系.2009年，Sanwong等[3]刻画了T(X，Y)中的极大、极小同余.2011年，Sanwong[4]研究了F(X，Y)的格林关系，并且得到了F(X，Y)的极大正则子半群的完全分类.文献[4]指出，对任意α，β∈F(X，Y)，

αLβ⟺im(α)=im(β)，

αRβ⟺ker(α)=ker(β)，

αJβ⟺|im(α)|=|im(β)|.

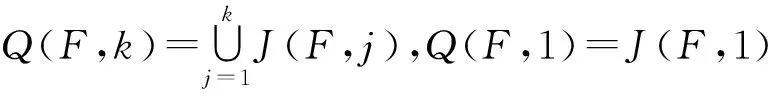
对任意α∈Q(F，1)，则显然Q(F，1){α}是Q(F，1)的极大正则子半带.当|Y|=n且2≤k≤n-1时，本文考虑半群Q(F，k)的极大正则子半带，得到了它的极大正则子半带的完全分类.

关于F(X，Y)还有以下基本事实：F(X，Y)的理想构成一个链，即

Q(F，1)⊂Q(F，2)⊂…⊂Q(F，n-1)⊂Q(F，n)=F(X，Y).

F(X，Y)的每一个主因子是一个Rees商半群Q(F，k)Q(F，k-1)，记为Pk.为方便起见，可将Pk视为J(F，k)∪{0}，即Pk=J(F，k)∪{0}，其乘法定义为

Pk对上述乘法做成一个完全0-单半群.

设U是半群S的任意子集，通常用E(U)表示U中的幂等元之集；对任意x∈S，用V(x)表示x在S中的所有逆元之集；Rx，Lx，Hx是分别表示x所在R-类，L-类，H-类.

设S是半群.为方便起见，本文用LS，RS，JS，DS分别表示S上的格林L，R，J，D关系.

关于完全0-单半群，有下述两个事实：

引理1[6]设x，y是完全0-单半群中两个非零元，则xy≠0，当且仅当Lx∩Ry中含有幂等元.此时xy∈Ly∩Rx.

引理2[6]设S是一个完全0-单半群，x，y是完全0-单半群中两个非零元，则：

设T(Y)是Y上的全变换半群.令SingY={α∈T(Y)||im(α)|≤n-1}，其中|Y|=n，则由Howie[7]的结果可知SingY中的格林关系有如下刻画：对任意α，β∈SingY，有

αLSingYβ⟺im(α)=im(β)，

αRSingYβ⟺ker(α)=ker(β)，

αJSingYβ⟺|im(α)|=|im(β)|.

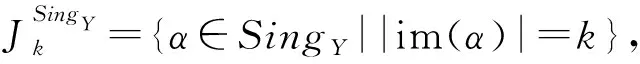
2 主要结果及证明

对任意α∈F(X，Y)，易验证α有如下表示法(称为α的标准表示)：

其中{a1，a2，…，ak}⊆Y，Aj∩Y≠∅，1≤j≤k.

引理3设2≤k≤n-1，α∈J(F，k)，则|E(Rα)|≥2且|E(Lα)|≥2.

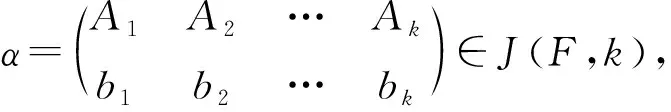
显然ε，η∈E(Rα)，因此|E(Rα)|≥2.设C=X{b2，…，bk}且D=X{b1，b2，…，bk-1}，令

显然δ，γ∈E(Lα)，因此|E(Lα)|≥2.

引理4设2≤k≤n-1，α∈J(F，k)，则存在α1，α2∈V(α)∩J(F，k)，使得(α1，α2)∉R且(α1，α2)∉L.

证明由引理3可知|E(Rα)|≥2，|E(Lα)|≥2.任意取ε1，ε2∈E(Rα)，η1，η2∈E(Lα)，ε1≠ε2，η1≠η2，则(ε1，ε2)∉L且(η1，η2)∉R(否则，ε1，ε2∈Hα或η1，η2∈Hα，与每一个H-类至多有一个幂等元矛盾).由εiRαLηi(i=1，2)及Miller-Clifford定理，Lε1∩Rη1和Lε2∩Rη2包含α的逆元，不妨分别设为α1和α2，于是αiLεi，αiRηi(i=1，2)，从而(α1，α2)∉L且(α1，α2)∉R.此外，由αiLεiRα可知αiJα，于是|im(αi)|=|im(α)|=k，从而αi∈J(F，k).

引理5设2≤k≤n-1，α∈J(F，k)，则J(F，k)Rα⊆〈E(J(F，k)Rα)〉.

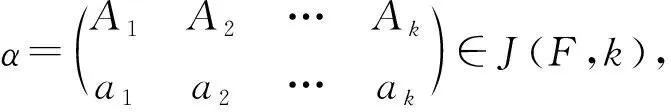
令α*=α|Y，β*=β|Y，则

下面分两种情形来讨论.

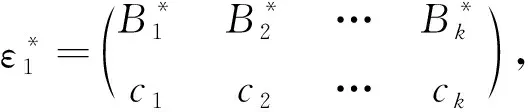
引理6设2≤k≤n-2，β∈J(F，k)，则J(F，k)Lβ⊆〈E(J(F，k)Lβ)〉.

证明利用文献[8]的结果，类似引理5的证明可得结论.

引理7设2≤k≤n-1，则Q(F，k)=〈E(J(F，k))〉且Q(F，k)是正则的.

证明见文献[5]中引理3.5与4.2以及文献[4]中引理7.

引理8设2≤k≤n-1，α∈J(F，k)，则M(α)=Q(F，k-1)∪(J(F，k)Rα)是Q(F，k)的极大正则子半带.

证明由Q(F，k-1)是Q(F，k)的理想可知要证M(α)是半群，只需证明对任意β，γ∈J(F，k)Rα，有βγ∈M(α).显然βγ∈Q(F，k-1)或βγ∈J(F，k).若βγ∈J(F，k)，则根据引理1可知βγ∈Lγ∩Rβ，于是βγ∈Rβ≠Rα，从而βγ∈J(F，k)Rα.因此M(α)是Q(F，k)的子半群.

由引理7可知Q(F，k-1)是正则的.对任意β∈J(F，k)Rα，由引理4，存在β1，β2∈V(β)∩J(F，k)，使得(β1，β2)∉R，于是β1，β2中必有一个属于J(F，k)Rα，即J(F，k)Rα中必存在β的逆元，从而β是正则的，进而M(α)是正则半群.再由引理5与引理7可得M(α)是幂等元生成的，因此M(α)是正则半带.

假设S是Q(F，k)的正则子半带，使得M(α)⊂S.任取β∈SM(α)，则β∈Rα.由引理3知|E(Lβ)|≥2，不妨设ε，η∈E(Lβ)且ε≠η，则ε，η中必有一个不属于Rα(否则，ε，η∈Hα，与每一个H-类至多有一个幂等元矛盾).不妨设ε∉Rα，于是Rε⊆J(F，k)Rα⊆M(α)⊂S，进而由引理2可得Rα=Rβ=βRε⊂S.从而S=Q(F，k)，M(α)是Q(F，k)的极大正则子半带.

引理9设2≤k≤n-2，β∈J(F，k)，则N(β)=Q(F，k-1)∪(J(F，k)Lβ)是Q(F，k)的极大正则子半带.

证明利用引理6，类似引理8的证明，可得结论.

对任意a∈Y，定义Sa={α∈J(F，n-1)|aα=a}，Aa=Q(F，n-2)∪Sa.

引理10设a∈Y，Na={α∈J(F，n-1)|im(α)=Y{a}}，则Aa=Q(F，n-2)∪〈E(J(F，n-1)Na)〉.

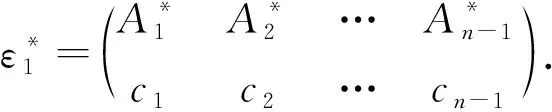
易验证E(J(F，n-1)Na)⊆Sa，于是〈E(J(F，n-1)Na)〉⊆〈Sa〉，从而Q(F，n-2)∪〈E(J(F，n-1)Na)〉⊆Q(F，n-2)∪〈Sa〉=Q(F，n-2)∪Sa=Aa.因此Aa=Q(F，n-2)∪〈E(J(F，n-1)Na)〉.

引理11设a∈Y，则Aa是Q(F，n-1)的极大正则子半带.

证明首先证明Aa是Q(F，n-1)的子半群.只需证明对任意α，β∈Sa且αβ∈J(F，n-1)，αβ∈Sa.由α，β∈Sa可知a(αβ)=(aα)β=aβ=a，从而αβ∈Sa.因此Aa是Q(F，n-1)的子半群.

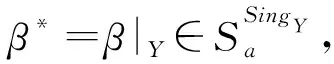
最后，证明Aa是Q(F，n-1)的极大正则子半带.假设S是Q(F，n-1)的正则子半带，满足Aa⊂S=〈E(S)〉⊆Q(F，n-1)=〈E(J(F，n-1))〉，由引理10知Aa=Q(F，n-2)∪〈E(J(F，n-1)Na)〉，从而E(Na)∩E(S)≠∅.不妨设ε∈E(Na)∩E(S)，注意到Na是J(F，n-1)的一个L-类，任取η∈E(Na)∩E(S)，则由引理3可得存在γ∈E(Rε)且γ∉Na(γ∈Aa⊂S)，于是由η∈E(Lε∩Rγ)及引理1可知εη∈Rε∩Lγ∩S.注意到ε，η∈E(S)且εRεγLγ，再由Miller-Clifford定理可得存在δ∈V(εη)∩S，使得δ∈Lε∩Rη=Lη∩Rη=Hη，于是δ是群Hη中的元，从而存在m∈N，使得η=δm∈S，故η∈E(S).由η的任意性可知E(Na)⊆E(S)，于是E(J(F，n-1))⊆E(S)，再由引理7可得S=Q(F，n-1).

定理1设2≤k≤n-2，则半群Q(F，k)的极大正则子半带有且仅有如下两类：

(ⅰ)M(α)=Q(F，k-1)∪(J(F，k)Rα)，α∈J(F，k)；

(ⅱ)N(β)=Q(F，k-1)∪(J(F，k)Lβ)，β∈J(F，k).

证明由引理8—9可知M(α)，N(β)是Q(F，k)的极大正则子半带.

假设T是Q(F，k)的极大正则子半带，但不是定理1中的形式，则对任意α∈J(F，k)，有E(T)∩E(Rα)≠∅且E(T)∩E(Lα)≠∅.否则，存在α∈J(F，k)，使得E(T)∩E(Rα)=∅或E(T)∩E(Lα)=∅，于是E(Rα)⊆E(J(F，k)T)或E(Lα)⊆E(J(F，k)T)，从而E(T)⊆M(α)⊂Q(F，k)或E(T)⊆N(α)⊂Q(F，k)，进而T=〈E(T)〉⊆M(α)⊂Q(F，k)或T=〈E(T)〉⊆N(α)⊂Q(F，k).由T是Q(F，k)的极大子半带可得T=M(α)或T=N(α)，矛盾.

下面证明E(J(F，k))⊆E(T).假设E(J(F，k))E(T)≠∅，任取ε∈E(J(F，k))E(T)⊆J(F，k)，则E(T)∩E(Lε)≠∅，E(T)∩E(Rε)≠∅.取η∈E(T)∩E(Lε)，γ∈E(T)∩E(Rε)，由引理1可得ηγ∈Rη∩Lγ∩T.再由Miller-Clifford定理可知存在δ∈V(ηγ)∩T，使得δ∈Lη∩Rγ=Rε∩Lε=Hε，进而δ是群Hε中的元.故存在m∈N，使得ε=δm∈T，这与ε∈E(J(F，k))E(T)矛盾，从而E(J(F，k))⊆E(T).再由引理7可得Q(F，k)=〈E(J(F，k))〉⊆〈E(T)〉=T，这与T是Q(F，k)的极大子半带矛盾.

定理2半群Q(F，n-1)的极大正则子半带有且仅有如下两类：

(ⅰ)Aa=Q(F，n-2)∪Sa，a∈Y；

(ⅱ)B(α)=Q(F，n-2)∪(J(F，n-1)Rα)，α∈J(F，n-1).

证明由引理8，11可知Aa，B(α)是Q(F，n-1)的极大正则子半带.

由引理10可知Aa=Q(F，n-2)∪〈E(J(F，n-1)Na)〉.注意到{Na|a∈Y}是J(F，n-1)所有L-类构成的集合.假设T是Q(F，n-1)的极大正则子半带，但不是定理2中的形式，则对任意α∈J(F，n-1)，a∈Y，有E(T)∩E(Na)≠∅且E(T)∩E(Rα)≠∅.否则，存在α∈J(F，n-1)，使得E(T)∩E(Rα)=∅或存在a∈Y，使得E(T)∩E(Na)=∅，于是E(T)⊆B(α)或E(T)⊆Aa，从而T=〈E(T)〉⊆B(α) 或T=〈E(T)〉⊆Aa.再由T是Q(F，n-1)的极大子半带可得T=B(α)或T=Aa，矛盾.

注意到{Na|a∈Y}是J(F，n-1)所有L-类构成的集合.类似定理1的证明可得E(J(F，n-1))⊆E(T)，从而由引理7可得Q(F，n-1)=〈E(J(F，n-1))〉⊆〈E(T)〉=T，这与T是Q(F，n-1)的极大子半带矛盾.

[参 考 文 献]

[1] SYMON J S V.Some results concerning a transformation semigroup[J].J Aust Math Soc，1975，19A(4)：413-425.

[2] SANWONG J，SOMMANEE W.Regularity and Green’s relations on a semigroup of transformations with restricted range[J/OL].Int J Math Sci，2008[2016-11-24].doi：10.1155/2008/794013.

[3] SANWONG J，SINGHA B，SULLIVAN R P.Maximal and minimal congruences on some semigroup[J].Acta Math Sin，2009，25(3)：455-466.

[4] SANWONG J.The regular part of a a semigroup of transformations with restricted range[J].Semigroup Forum，2011，83(1)：134-146.

[5] SANWONG J，SOMMANEE W.Rank and idempotent rank of finite full transformations semigroup with restricted range[J].Semigroup Forum，2013[2016-11-24].doi：10.1007/s00233-013-9467-x.

[6] HOWIE J M.Fundamentals of semigroup theory[M].Oxford：Oxford Press，1995：1-154.

[7] HOWIE J M.The subsemigroup generated by the idempotents of a full transformation semigroup[J].J London Math Soc，1966，41：707-716.

[8] ZHAO PING，HU H B，YOU T J.A note on maximal regular subsemigroups of the finite transformation semigroupsT(n，r)[J].Semigroup Forum，2014，88：324-332.

[9] YANG XIULIANG，YANG H.Maximal regular subsemibands of singn[J].Semigroup Forum，2006，72：75-93.