Rota-Baxter 3-超代数的构造

王 波，刘贵来，魏 竹

(东北师范大学数学与统计学院，吉林 长春 130024)

0 引言

Rota-Baxter代数是由数学家Glen E Baxter在1960年提出的，随后众学者进行了广泛研究.[1-3]李代数中满足Rota-Baxter等式的线性算子是由Belavin引入的，之后由物理学家杨振宁和Rodney Baxter命名.近年来，Rota-Baxter代数在理论物理和数学中有许多应用并取得了丰硕的研究成果，主要包括量子场论[4]、Yang-Baxter方程[5-7]、Hopf代数[8-9]与Rota-Baxter 3-Lie代数[10-11].Rota-Baxter算子在应用数学中也有广泛应用.

1974年，物理学家Wess和Zumion为了建立相对论的费米子与玻色子的统一理论，提出了超对称性概念，将普通时空满足的Poincaré代数(即非齐次Lorentz代数)扩充为超Poincaré代数[12]，将有限个不同内部量子数的玻色子与费米子放在李超代数的一个不可约表示中，从此李超代数引起数学工作者的研究兴趣.

受Rota-Baxter代数和超代数研究的启发，本文给出了超导子、Rota-Baxter 3-李超代数及Rota-Baxter李超三系的定义，并给出在这两个超代数上分别通过重新定义偶三元线性映射来构造新Rota-Baxter 3-李超代数和Rota-Baxter李超三系的方法.

1 Rota-Baxter 3-超代数的超导子

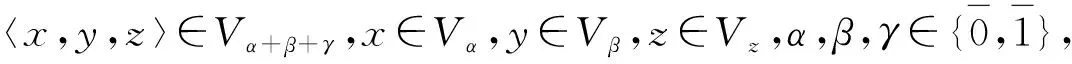
定义1.2设(V，·)是域K上的超代数.若V上的偶线性映射D：V→V满足

D(x·y)=D(x)·y+x·D(y)，∀x，y∈V，

(1)

则称映射D为V的超导子，所有超导子的集合记为Der(V).更一般地，若V上的偶线性映射d：V→V满足

d(x·y)=d(x)·y+x·d(y)+λx·y，∀x，y∈V，λ∈K，

(2)

则称映射d为V上权为λ的超导子.

定义1.3设3-超代数(V，〈，，〉)上偶线性映射d：V→V满足等式

〈d(x1)，x2，x3〉+〈x1，d(x2)，x3〉+〈x1，x2，d(x3)〉+

λ〈d(x1)，d(x2)，x3〉+λ〈d(x1)，x2，d(x3)〉+
λ〈x1，d(x2)，d(x3)〉+λ2〈d(x1)，d(x2)，d(x3)〉，

(3)

定义1.4设(V，·)是域K上的超代数.若V上的偶线性映射P：V→V满足

P(x)·P(y)=P(P(x)·y+x·P(y)+λx·y)，∀x，y，∈V，λ∈K，

(4)

则称(V，·，P)是域K上的Rota-Baxter超代数，称映射P为V的权为λ的Rota-Baxter超算子，称(4)式为Rota-Baxter超等式.

定义1.5设3-超代数(V，〈，，〉)上偶线性映射P：V→V满足

P(〈P(x1)，P(x2)，x3〉)+P(〈P(x1)，x2，P(x3)〉)+
P(〈x1，P(x2)，P(x3)〉)+λP(〈P(x1)，x2，x3〉)+
λP(〈x1，P(x2)，x3〉)+λP(〈x1，x2，P(x3)〉)+λ2P(〈x1，x2，x4〉)，

(5)

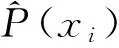
定理1.1设(V，〈，，〉)是域K上的3-超代数，则偶可逆线性映射P：V→V是权为λ的Rota-Baxter超算子的充分必要条件是P-1是3-超代数(V，〈，，〉)的权为λ的超导子.

证明设偶可逆线性映射P：V→V是权为λ的Rota-Baxter超算子，且对于∀x1，x2，x3∈V，令yi=p-1(xi)，i=1，2，3，由等式(5)有

P-1(〈x1，x2，x3〉)=P-1(〈P(y1)，P(y2)，P(y3)〉)=
P-1P(〈P(y1)，P(y2)，y3〉+〈P(y1)，y2，P(y3)〉+〈y1，P(y2)，P(y3)〉)+
λP-1P(〈P(y1)，y2，y3〉+〈y1，P(y2)，y3〉+〈y1，y2，P(y3)〉)+λ2P-1P(〈y1，y2，y3〉)=
〈x1，x2，P-1(x3)〉+〈x1，P-1(x2)，x3〉+〈P-1(x1)，x2，x3〉+λ(〈x1，P-1(x2)，P-1(x3)〉+
〈P-1(x1)，x2，P-1(x3)〉+〈P-1(x1)，P-1(x2)，x3〉)+λ2(〈P-1(x1)，P-1(x2)，P-1(x3)〉)，

故由(3)式可得P-1是超代数(V，〈，，〉)的权为λ的超导子.

反之，若P是超代数(V，〈，，〉)的权为λ的超导子，∀x1，x2，x3∈V，由等式(3)可得

P(〈P-1(x1)，P-1(x2)，P-1(x3)〉)=〈x1，P-1(x2)，P-1(x3)〉+
〈P-1(x1)，x2，P-1(x3)〉+〈P-1(x1)，P-1(x2)，x3〉+

λ〈x1，x2，P-1(x3)〉+λ(〈x1，P-1(x2)，x3〉+〈P-1(x1)，x2，x3〉)+λ2〈x1，x2，x3〉，

从而

〈P-1(x1)，P-1(x2)，P-1(x3)〉=P-1(〈x1，P-1(x2)，P-1(x3)〉+〈P-1(x1)，x2，P-1(x3)〉)+
P-1(〈P-1(x1)，P-1(x2)，x3〉+λ〈x1，x2，P-1(x3)〉)+
λP-1(〈x1，P-1(x2)，x3〉+〈P-1(x1)，x2，x3〉)+λ2P-1(〈x1，x2，x3〉).

2 从Rota-Baxter 3-李超代数构造Rota-Baxter 3-李超代数

定义2.1设V是域K上的向量超空间.若在V上定义偶三元线性映射[，，]：V⊗V⊗V→V，满足：

[x1，x2，x3]=-(-1)|x1||x2|[x2，x1，x3]，[x1，x2，x3]=-(-1)|x2||x3|[x1，x3，x2]，

(6)

[[x1，x2，x3]，y2，y3]=(-1)|x2||y2|+|x2||y3|+|x3||y2|+|x3||y3|[[x1，y2，y3]，x2，x3]+

(-1)|x3||y2|+|x3||y3|[x1，[x2，y2，y3]，x3]+[x1，x2，[x3，y2，y3]]，

(7)

∀x1，x2，x3，y2，y3∈V.则称(V，[，，])为3-李超代数，称(7)式为3-Jacobi超等式.

事实上，(7)式与下式等价：

[[x1，x2，x3]，y2，y3]=(-1)|x2||y2|+|x2||y3|+|x3||y2|+|x3||y3|[[x1，y2，y3]，x2，x3]+

(-1)|x1||x2|+|x1||y2|+|x1||y3|+|x3||y2|+|x3||y3|[[x2，y2，y3]，x1，x3]+

(-1)|x1||x3|+|x1||y2|+|x1||y3|+|x2||x3|+|x2||y2|+|x2||y3|[[x3，y2，y3]，x1，x2].

(8)

定义2.2设(V，[，，])是域K上的3-李超代数.若V上偶线性映射P：V→V满足

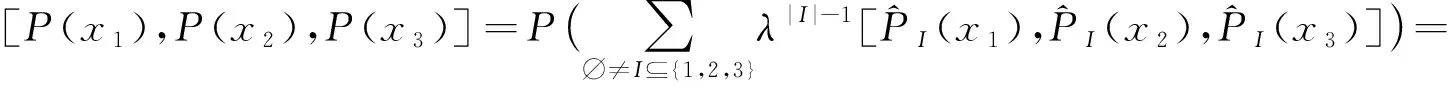
λP([x1，P(x2)，x3])+λP([x1，x2，P(x3)])+λ2P([x1，x2，x3])，

(9)

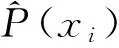
设(V，[，，]，P)是域K上权为λ的Rota-Baxter 3-李超代数，利用等式(5)，可在V上定义偶三元线性映射

[P(x)，P(y)，z]+[P(x)，y，P(z)]+[x，P(y)，P(z)]+

λ[P(x)，y，z]+λ[x，P(y)，z]+λ[x，y，P(z)]+λ2[x，y，z]，

(10)

∀x，y，z∈V，λ∈K.

定理2.1设(V，[，，]，P)是域K上权为λ的Rota-Baxter 3-李超代数.若在V上定义偶三元线性运算[，，]P满足等式(10)，则(V，[，，]P，P)是权为λ的Rota-Baxter 3-李超代数.

证明首先证明(V，[，，]P，P)是3-李超代数.显然[，，]P满足等式(6)，只需证明[，，]P满足3-Jacobi超等式即可.对于∀x1，x2，x3，x4，x5∈V，令y1=[x1，x2，x3]P，y2=x4，y3=x5，由等式(9)和(10)有

因为(V，[，，]，P)是3-李超代数，所以对于∅≠K⊆{1，2，3，4，5}有

(-1)|x1||x2|+|x1||x4|+|x1||x5|+|x3||x4|+|x3||x5|[[(x2)，(x4)，(x5)]，(x1)，(x3)]+
(-1)|x1||x3|+|x1||x4|+|x1||x5|+|x2||x3|+|x2||x4|+|x2||x5|[[(x3)，(x4)，(x5)]，(x1)，(x2)].

再证明Rota-Baxter等式成立即可.事实上，

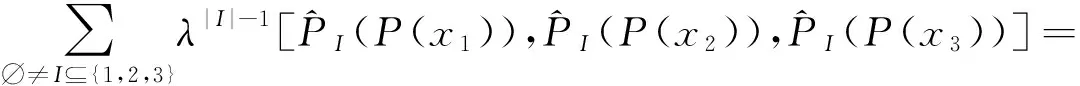
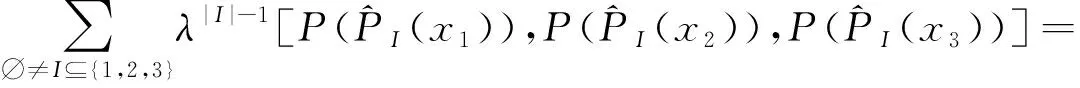
推论2.1[13]设(V，[，]，P)是域K上权为λ的Rota-Baxter李超代数，f∈L*，假设f，P满足f([x，y])=0，

(P+λid)(f(x)[P(y)，P(z)]+(-1)|x||y|+|x||z|f(y)[P(z)，P(x)]+
(-1)|x||z|+|y||z|f(z)[P(x)，P(y)])=0.

若定义

[x，y，z]f，P=f(P(x))([P(y)，z]+[y，P(z)]+λ[y，z])+

(-1)|x||y|+|x||z|f(P(y))([P(z)，x]+[z，P(x)]+λ[z，x])+

(-1)|x||z|+|y||z|f(P(z))([P(x)，y]+[x，P(y)]+λ[x，y])+

f(x)([P(y)，P(z)]+λ[P(y)，z]+λ[y，P(z)]+λ2[y，z])+

(-1)|x||y|+|x||z|f(y)([P(z)，P(x)]+λ[P(z)，x]+λ[z，P(x)]+λ2[z，x])+

(-1)|x||z|+|y||z|f(z)([P(x)，P(y)]+λ[P(x)，y]+λ[x，P(y)]+λ2[x，y])，

(11)

∀x，y，z∈V，λ∈K，则(V，[，，]f，P，P)是权为λ的Rota-Baxter 3-李超代数.

证明由文献[10]，∀x，y，z∈V，若定义

[x，y，z]f=f(x)[y，z]+(-1)|x||y|+|x||z|f(y)[z，x]+(-1)|x||z|+|y||z|f(z)[x，y]，

则(V，[，，]f，P)是权为λ的Rota-Baxter 3-李超代数.现定义[，，]∶=[，，]f，再利用等式(10)可以定义偶三元线性映射[，，]f，P，由定理2.1，(V，[，，]f，P，P)是权为λ的Rota-Baxter 3-李超代数，显然等式(11)成立.

3 从Rota-Baxter李超三系构造Rota-Baxter李超三系

定义3.1[10]设V是域K上的向量超空间.若在V上定义偶三元线性映射[，，]：V⊗V⊗V→V，满足：

[x，y，z]=-(-1)|x||y|[y，x，z]，

(12)

[x，y，z]+(-1)|x||y|+|x||z|[y，z，x]+(-1)|x||z|+|y||z|[z，x，y]=0，

(13)

[[x，y，z]，u，v]=(-1)|y||u|+|y||v|+|z||u|+|z||v|[[x，u，v]，y，z]+
(-1)|z||u|+|z||v|[x，[y，u，v]，z]+[x，y，[z，u，v]]，

(14)

∀x，y，z，u，v∈V.则称(V，[，，])为李超三系.

李超三系是3-李超代数，可以按照Rota-Baxter 3-李超代数的定义方式来定义Rota-Baxter李超三系.

定义3.2设(V，[，，])是李超三系.若V上偶线性映射P：V→V满足

[P(x)，P(y)，P(z)]=[P(x)，P(y)，z]+[P(x)，y，P(z)]=

[x，P(y)，P(z)]+λ[x，y，P(z)]+λ[x，P(y)，z]+λ[P(x)，y，z]+λ2[x，y，z]，

(15)

∀x，y，z∈V，λ∈K，则称(V，[，，]，P)是权为λ的Rota-Baxter李超三系.

定理3.1设(V，[，，]，P)是权为λ的Rota-Baxter李超三系.若在V上定义偶三元线性映射[，，]P：V⊗V⊗V→V满足等式(10)，则(V，[，，]P，P)是权为λ的Rota-Baxter李超三系.

证明由于(V，[，，]，P)是权为λ的Rota-Baxter李超三系，∀x，y，z，u，v∈V，显然有

[x，y，z]P=-(-1)|x||y|[y，x，z]P，

[x，y，z]P+(-1)|x||y|+|x||z|[y，z，x]P+(-1)|x||z|+|y||z|[z，x，y]P=0.

再根据定理2.1，

[[x，y，z]P，u，v]P=(-1)|y||u|+|y||v|+|z||u|+|z||v|[[x，u，v]P，y，z]P+
(-1)|z||u|+|z||v|[x，[y，u，v]P，z]P+[x，y，[z，u，v]P]P.

由等式(10)和(9)，

[P(x)，P(y)，P(z)]P=[P2(x)，P2(y)，P(z)]+
[P2(x)，P(y)，P2(z)]+[P(x)，P2(y)，P2(z)]+

λ[P2(x)，P(y)，P(z)]+λ[P(x)，P2(y)，P(z)]+
λ[P(x)，P(y)，P2(z)]+λ2[P(x)，P(y)，P(z)]=

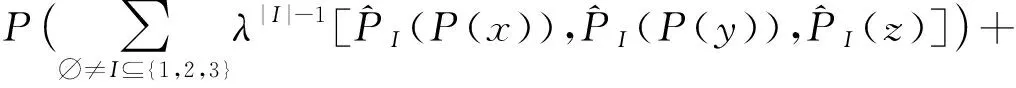
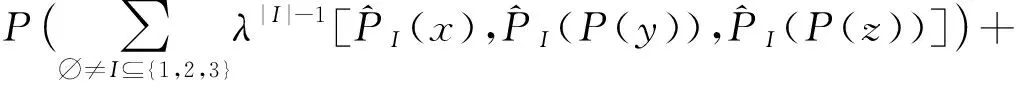
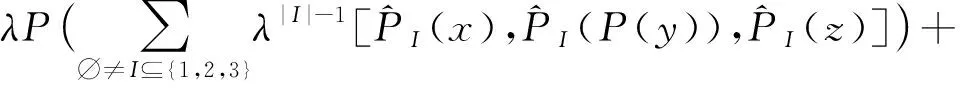
P([x1，P(x2)，P(x3)]P)+λP([P(x1)，x2，x3]P)+
λP([x1，P(x2)，x3]P)+λP([x1，x2，P(x3)]P)+λ2P([x1，x2，x3]P).

定理3.2设(V，[，]，P)是权为λ的Rota-Baxter李超代数.若在V上定义偶三元线性映射[，，]：V⊗V⊗V→V满足

[x，y，z]∶=[x，[y，z]]，∀x，y，z∈V，

(16)

则(V，[，，]，P)是权为λ的Rota-Baxter李超三系.

证明由文献[10，14]，若(V，[，])是李超代数，则(V，[，，])是李超三系([，，]满足等式(16)).由(4)和(16)式，∀x，y，z∈V，

[P(x)，[P(y)，P(z)]]=[P(x)，P([y，P(z)])]+
[P(x)，P([P(y)，z])]+λ[P(x)，P([y，z])]=

P([P(x)，[y，P(z)]])+P([x，P([y，P(z)])])+λP([x，[y，P(z)]])+

P([P(x)，[P(y)，z]])+P([x，P([P(y)，z])])+λP([x，[P(y)，z]])+

λP([P(x)，[y，z]])+λP([x，P([y，z])])+λ2P([x，[y，z]]).

因为

P([x，[P(y)，P(z)]])=P([x，[y，P(z)]])+P([x，P([P(y)，z])])+λP([x，P([y，z])])，

从而

[P(x)，P(y)，P(z)]=[P(x)，[P(x)，P(y)]]=
P([P(x)，[P(y)，z]])+P([P(x)，[y，P(z)]])+P([x，[P(y)，P(z)]])+

λP([P(x)，[y，z]])+λP([x，[P(y)，z]])+λP([x，[y，P(z)]])+λ2P([x，[y，z]])=

P([P(x)，P(y)，z])+P([P(x)，y，P(z)])+([x，P(y)，P(z)])+

λP([P(x)，y，z])+λP([x，P(y)，z])+λP([x，y，P(z)])+λ2P([x，y，z]).

[参 考 文 献]

[1] CONNES A，KREIMER D.Hopf algebras renormalization and noncommu-tative geometry[J].Comm Math Phys，1998，199(1)：203-242.

[2] EBRAHIMII-FARD K，GUO L，KREIMER D.Spitzer’s identity and the alge-braic birkhoff decomposition in pQFT[J].Phys A：Math Gen，2004，37(1)：11037-11052.

[3] EBRAHIMII-FARD K，GUO L，KREIMER D.Birkhoff type decompositions and the Baker-Campbell-Hausdorff recursion[J].Comm Math Phys，2006，267(3)：821-845.

[4] FILIPPOV V T.N-Lie algebra[J].Sib Mat Zh，1985，26(10)：126-140.

[5] GUO L.What is a Rota-Baxter algebras[J]. Notice Amer Math Soc，2009，56(11)：1436-1437.

[6] GUO L.Introduction to Rota-Baxter algebras[M].Peking：International Press and Higher Education Press，2012：47-98.

[7] GUO L，KEIGHER W.Introduction to Rota-Baxter algebras[J].Adv Math，2000，151(1)：101-127.

[8] GUO L，KEIGHER W.On differential Rota-Baxter algebras[J].Pure Appl Algebra，2008，212(3)：522-540.

[9] GUO L，SIT W，ZHANG R.Differential type operators and Gröbne-Shirshov bases[J].Symolic Comput，2012，52(5)：97-123.

[10] BAI R，GUO L，LI J，WU Y.Rota-Baxter 3-Lie algebras[J].J Math Phy，2013，54(6)：295-308.

[11] SUN B，CHEN L.Rota-Baxter multiplicative 3-ary Hom-Nambu algebras[J].Journal of Geometry & Physics，2015(98)：400-413.

[12] 孙洪洲，韩其智.李超代数综述[J].物理学进展，1983，3(1)：81-125.

[13] BAI R，BAI C，WANG J.Realizations of 3-Lie algebra[J/OL].J Math Phy，2010[2016-12-26].https：//doi.org/10.1063/1.3436555.

[14] LITER W.A structure theory of Lie triple systems[J].Trans Amer Math Soc，1952，72(2)：217-217.