路与路的强积的r-多彩染色

邵瑞芳，左连翠

（天津师范大学数学科学学院，天津 300387）

1 引言和预备知识

本文考虑的图都是连通有限的无向图，并且没有重边.用[a，b]表示从a到b的所有整数，b≥a＞0.

对于图 G=（V，E）的一个顶点染色 c：V（G）→[1，k]，如果相邻2个顶点着不同的颜色，则这种染色称为正常染色，使得图G为正常染色所使用的最少色数k，称为图G的正常色数，用χ（G）来表示.图G的r-多彩k-染色是一个使用k种颜色的正常染色c：V（G）→[1，k]，并且对于图 G 中每个度为 d（v）的顶点v，满足|c（N（v））|≥min{d（v），r}，其中 N（v）表示顶点 v的邻点集，c（N（v））={c（u），u∈N（v）}，使得图 G 为r-多彩k-染色的最小整数k称为图G的r-多彩色数，用χr（G）来表示.显然有χ（G）≤χr（G）.

对于r-多彩染色，国内外许多学者进行了研究.文献[1]证明了当3|n时，χ2（Cn）=3，当n=5时，χ2（Cn）=5，其他情况χ2（Cn）=4.文献[2]证明了如果图G是一个强正则图（不包含C5和完全二部图），则χ2（G）-χ（G）≤1.文献[3]证明了对于任意k-正则图，有χ2（G）≤χ（G）+14.06 ln k+1.文献[4]证明了对任何正整数n，都存在一个正常色数为n的正则图，满足χ2（G）-χ（G）≥1.关于图的二元运算，文献[5]证明了如果G和H是2个简单图，且 δ（G）≥2，δ（G）表示图 G的最小度，那么有χ2（G□H）≤max{χ2（G），χ（H）}，G□H表示图G和H的笛卡尔乘积.文献[6]证明了对于2个简单图G和H，若δ（G）≥r，那么有χr（G□H）≤max{χr（G），χ（H）}.文献[7]证明了若 mn≡2（mod 4），m × n 网格不存在3-多彩4-染色.文献[8]研究了网格和超环面的r-多彩染色.文献[9]证明了若G和H是2个简单图，并且δ（G）≥r，则χr（G×H）≤χr（G），其中G×H表示图G和图H的直积，同时获得了一些图的多彩色数的确切值.

设G和H是2个简单图，G和H的强积用G□H表示，其顶点集为V（G）×V（H），边集为X∪Y∪Z，其中：

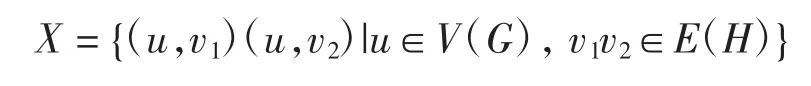
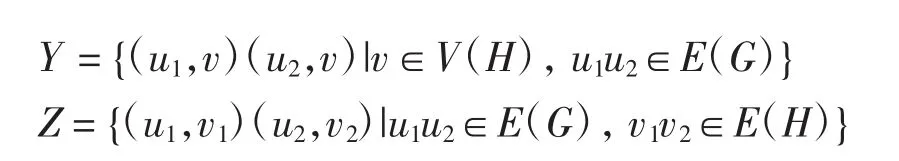
显然.本文考虑路与路强积的r-多彩染色，并给出了其r-多彩色数的确切值.

引理1χr（G）≥min{Δ（G），r}+1，对于树等号成立.

引理2如果r≥Δ（G），那么χr（G）=χΔ(G）（G）.

引理3χr+1（G）≥χr（G），r≥2.

2 主要结论

定理设Pm=u1u2…um和Pn=v1v2…un分别为m阶和n阶的路，n、m≥2，且n、m是正整数，则有如下结论.

当r≥8时，有

证明设.根据强积图的定义，Pn和Pm满足交换律，可以假设m≥n≥2.

首先，当 m=n=2 时，顶点（u1，v1）、（u1，v2）、（u2，v1）、（u2，v2）构成的图是一个K4，则χr（G）=4，r≥2.

以下设m≥3.

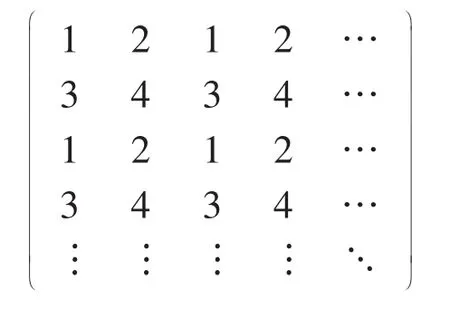
c是图G的一个2-多彩染色，所以χ2（G）≤4.因此χ2（G）=4.

（2）对于，利用与（1）相同的方法，可以证明χ3（G）=χ2（G）=4.

（3）对于，由引理1，此时有χ4（G）≥5.定义如下染色c

其中c（ui+1，v5k+j）=c（ui，vp），p≡（j+3）（mod 5），p∈[1，5].c是图G的一个4-多彩染色，所以χ4（G）≤5.因此χ4（G）=5.

（4）对于，由引理1，此时有χ5（G）≥6.

情况1n=2.能够定义如下染色c

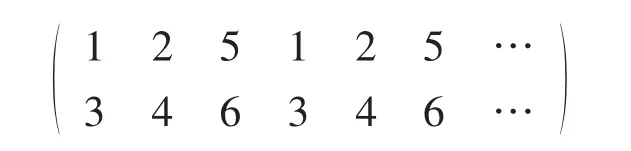
很明显，c是图G的一个5-多彩染色，所以χ5（G）≤6.因此χ5（G）=6.

情况 2n≥3.可以假设 c（u1，v1）=1，c（u1，v2）=2，c（u2，v1）=3，c（u2，v2）=4，由 r-多彩染色的定义，有 c（u1，v3）=5，c（u2，v3）=6，c（u3，v2）∉[1，6]，因此χ5（G）≥7.

情况2.1n=3.定义如下染色c

其中：c（ui，v4k+j）=c（ui，vj），i=1、3，j∈[1，4]；c（u2，v3k+j）=c（u2，vj），j∈[1，4].c是图G的一个5-多彩染色，所以χ5（G）≤7.因此，在这种情况下χ5（G）=7.

情况2.2n≥3.由情况2.1和r-多彩染色的定义，有c（u4，v1）=7，c（u4，v2）∉[1，7]，所以χ5（G）≥8.定义如下染色c

其中c（ui+2，vj）=c（ui，vp），p≡（j+2）（mod 4），p∈[1，4].c是图G的一个5-多彩染色，所以χ5（G）≤8.因此，在这种情况下χ5（G）=8.

（5）对于.

情况1n=2.此时Δ（G）=5，由引理2有χ6（G）=χ5（G）=6.

情况2n≥3.

情况2.1n=3.由引理2，此时结果与（4）情况2.1相同，因此χ6（G）=7.

情况2.2n≥4.由引理3，此时有χ6（G）≥χ5（G）=8.定义如下染色c

c是图G的一个6-多彩染色，所以χ6（G）≤8.因此，在这种情况下.

（6）对于χ7（PnPm）.

情况1n=2.在这种情况下，Δ（G）=5，由引理2有χ7（G）=χ5（G）=6.

情况2n≥3，由引理1有χ7（G）≥8.能够定义如下染色c

其中c（ui+3，vj）=c（ui，vp），p≡j（mod 8），p∈[1，8].c是图G的一个7-多彩染色，所以χ7（G）≤8.因此，在这种情况下χ7（G）=8.

（7）对于，r≥8.在这种情况下，由引理2可知χr（G）=χ8（G）.

情况1n=2.在这种情况下，Δ（G）=5，由引理2有χr（G）=χ5（G）=6.

情况2n≥3.由引理1，此时有χ8（G）≥9.定义如下染色c

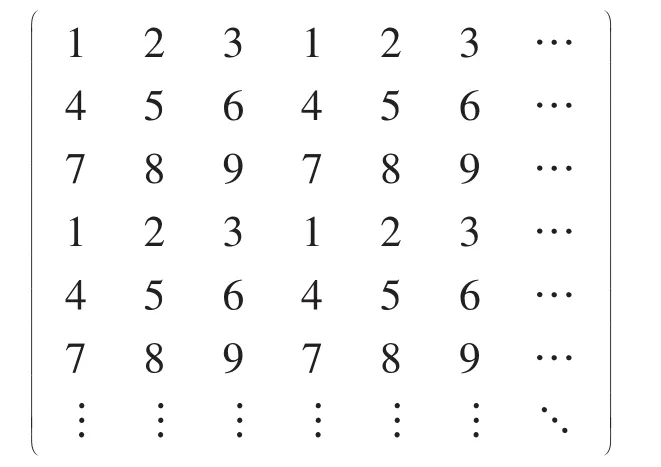
很明显，c是图G的一个r-多彩染色，所以χr（G）≤9.因此，在这种情况下χr（G）=9.

[1]MONTGOMERY B.Dynamic Coloring of Graphs[D].Morgantown：West Virginia University，2001.

[2]AKBARIS，GHANBARIM，JAHANBAKEMS.Onthedynamic coloring of strongly regular graphs[J].IEEE International Conference on Systems，2011，32（14）：257-264.

[3]ALISHAHI M.On the dynamic coloring number of graphs[J].Discrete Applied Mathematics，2011，159（2/3）：152-156.

[4]ALISHAHI M.Dynamic chromatic number of regular graphs[J].Discrete Applied Mathematics，2012，160（15）：2098-2103.

[5]AKBARI S，GHANBARI M，JAHANBEKAM S.On the dynamic coloring of Cartesian product graphs[J].Ars Combinatoria，2014，114（4）：161-168.

[6]SUIL O.Edge-connectivity，Eigenvalues，and Matchings in Regular Graphs[D].Urbana：University of Illinoist，2011.

[7]KANG R，MULLER T，WEST D B.On r-dynamic coloring of gird[J].Discrete Applied Mathematics，2014，186（1）：286-290.

[8]JAHANBEKAM S，KIM J，SUIL O，et al.On r-dynamic coloring of graphs[J].Discrete Applied Mathematics，2016，206（C）：65-72.

[9]张冰.几类图的r-hued染色和距离标号[D].徐州：中国矿业大学，2016.ZHANGB.The r-huedColoringandDistanceLabelingofSeveralClasses of Graphs[D].Xuzhou：China University of Mining and Technology，2016（in Chinese）.