异构多机器人编队相互通信时延精确控制
贾 枭,张国良,徐 君,杜柏阳,林志林
火箭军工程大学 301教研室,西安 710025
1 引言
多机器人编队控制是指系统中各个机器人利用通信协议,通过分布式控制形成并保持既定几何构型,在卫星编队、无人机编队、多机械臂系统、集群机器人救护等方面得到广泛应用研究[1-3]。编队控制由此成为多机器人协同控制领域研究的热点问题。
Jadbabaie等[4]运用代数图论知识证明了多智能体系统存在一致性,进而为基于一致性理论的编队控制研究奠定基础。Jiang等[5]利用采样控制方法研究了一阶多机器人系统的一致性问题。考虑多机器人系统编队的实际环境,系统中个体交换信息不可避免存在通信时延,所以在多机器人系统的一致性研究中,时延问题一直是研究的重点[6-7]。连续系统方面,Liu等[8]采用容积控制方法对二阶多机器人系统的时变时延问题进行分析,并推导得到系统实现一致性的充分条件。离散系统方面,Zhong等[9]基于模型预测控制方法对二阶的离散时延问题进行了研究。进一步考虑高阶系统,Xi等[10]通过引入一致性子空间及其补子空间,将高阶线性时变系统的一致性问题转化为带有时延的低维子系统的稳定性问题。
现在许多编队控制一致性分析都是针对同构系统而言的,即假设多机器人系统中所有个体具有相同的动力学模型,然而此种假设在很多应用中是不符合实际情景的。于是,众多学者开始对异构系统展开研究。连续系统方面,郑元世等[11]利用图论和Lyapunov稳定性理论得出异构系统在无向拓扑图中实现一致性的充分条件。Kim等[12]针对异构系统在有无领导者两种情形的一致性问题,基于Lyapunov理论设计一致性协议,并证明其收敛性。离散系统方面,Liu等[13]研究了离散时间异构多智能体一致性问题,得到了离散系统实现一致性的充分条件。
上述文献[11-13]从不同角度对异构多机器人系统编队控制进行研究,取得了一些研究成果。以上研究都是基于无向通信拓扑,但是在现实环境中,系统的各个机器人不可能始终保持相互通信,因此对于有向通信拓扑情况下异构多机器人系统的编队控制研究更具实际工程意义。此外,虽然目前对同构系统的时延问题研究较为成熟[6-9],但是当异构多机器人系统存在时延时,同时对系统中不同阶机器人进行一致性分析的难度增大,而学者们对此类问题的研究依旧较少。本文基于领航跟随者模式展开系统编队控制一致性的研究,对跟随者机器人提出一致性控制协议,降低了同时对不同阶机器人进行一致性分析的难度。
本文的主要工作在于考虑有向通信拓扑,在零时延和固定时延情况下,开展对异构多机器人系统的编队精确控制问题的研究。首先基于领航跟随者模式,分别针对零时延和固定时延时的一、二阶异构多机器人系统的编队控制问题,提出相应的一致性控制协议。然后利用图论与矩阵分析方法,得到零时延系统实现编队控制的充要条件。进一步构造Lyapunov-Razumikhin函数,分析得到固定时延系统在Lyapunov意义下稳定的充分条件。最后通过仿真算例,验证一致性控制算法的正确性。
2 异构多机器人编队模型建立
2.1 异构系统编队模型
采用领航跟随者法,建立异构多机器人系统编队模型。考虑由n+1个机器人组成的连续时间异构多机器人系统,其中一个一阶机器人为领航者,其余n个二阶机器人为跟随者。于是可将异构系统编队模型描述如下:

其中,p0(t),q0(t)∈ℝ为一阶机器人的位置和常速度;pi(t),qi(t),ui(t)∈ℝ为系统中二阶机器人的位置、速度和控制输入。
定义1对于异构编队系统(1),如果各状态量满足以下要求,则系统实现预期编队和渐近速度一致,完成编队任务[14]:

注1领航跟随者模式下的异构系统(1)编队控制问题的实质是设计合理的跟随者控制输入ui(t),使系统中各个跟随者的状态参量与领航者达到一致。因此针对系统(1)的不同时延情况,设计与选择合适的控制输入ui(t)进行分析与讨论是实现异构多机器人系统编队控制的关键所在。
2.2 通信拓扑
针对基于领航跟随者模式的异构编队系统(1),定义拓扑图它表示节点集为边集为,跟随者邻接矩阵为的异构多机器人系统,其中v0表示领航者,vk(k=1,2,…,n)表示跟随者。如果领航者v0与其他每个跟随者vk(k =1,2,…,n)之间都存在一条有向路径,那么称领航者v0全局可达。同时,为描述各跟随者与领航者之间的邻接关系定义B=diag(bii)(i =1,2,…,n),如果跟随者vk(k =1,2,…,n)与领航者v0之间存在直接通信链路即bii>0否则bii=0。
根据附加权重的有向图邻接关系的定义,通常以Laplacian矩阵L表示一个图。它定义为:

3 编队控制一致性算法
一致性算法是指针对异构编队系统的输入ui(t)设计合理的一致性控制协议,从而使系统各个个体的状态量达到一致。此算法具有较强的工程实践意义,因此广泛应用于多机器人的编队控制研究[4-14]。针对异构编队系统(1),在零时延和固定时延两种情况下提出相应的一致性控制协议。
3.1 零时延一致性协议设计
针对异构编队系统的零时延情形,提出如下一致性控制协议:

其中k>0表示控制参数,ri表示期望队形中各跟随者与领航者的相对距离。
令 p=[p1,p2,…,pn]T,q=[q1,q2,…,qn]T,r=[r1,r2,…,rn]T。将一致性协议(2)带入系统(1)跟随者模型中整理得到下面向量形式:

令 x=p-p0⊗1-r和v=q-q0⊗1,可以得到系统(3)的误差模型:
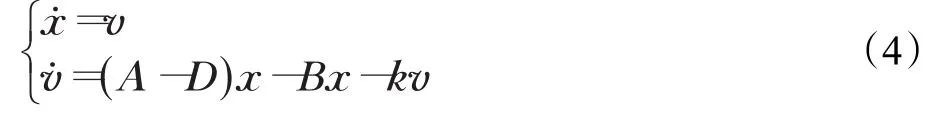
令那么误差系统(4)可以写成如下形式:

其中系统矩阵
3.2 固定时延一致性协议设计
针对异构编队系统的零时延情形,提出如下一致性控制协议:
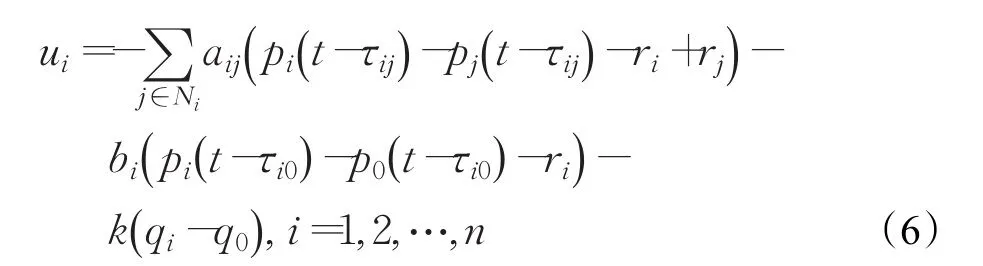
其中k>0表示控制参数,ri表示期望队形中各跟随者与领航者的相对距离,令τij=τji表示节点i与节点 j之间的通信时延。
为描述方便,令 τr∈{τij:i,j=1,2,…,n,i≠j} ,其中r=1,2,…,m(m ≤n(n -1) )。定义系统通信拓扑图Gˉ的子图,相应的邻接矩阵,度矩阵 D,Laplacian矩r阵Lr和领导者的邻接矩阵Βr[14]。由于每个子图不相关那么有
记 p=[p1,p2,…,pn]T,q=[q1,q2,…,qn]T,r=[r1,r2,…,rn]T。将一致性协议(6)带入系统(1)跟随者模型中整理得到下面向量形式:
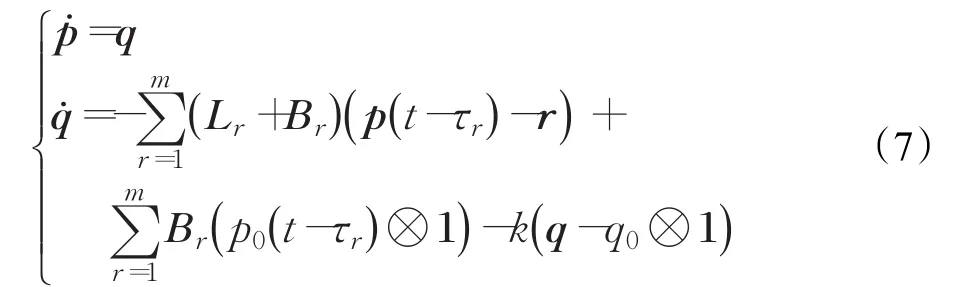
令同样的,可以得到系统(7)的误差模型:
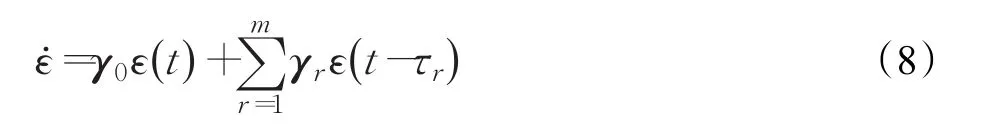
其中系统矩阵
注2针对零时延和固定时延情况下的异构系统编队控制问题,分别提出一致性算法,得到了相应的编队误差系统模型(5)与(8),从而将系统的编队控制一致性问题转化稳定性问题。算法的目标:当t→∞时,ε(t)→0即实现稳定的异构系统编队控制。
4 编队控制一致性分析
主要是对误差系统(5)与(8)进行稳定性分析,确定系统的控制参数k与时延τr的范围,得到系统在零时延和固定时延两种情况下实现编队控制的基本条件。
4.1 零时延编队控制分析
定理1,控制参数k满足k2>(Re表示实部,Im表示虚部),同时 minμ∈ρ(F)Reμ≠0,其中 ρ(F )表示n×n矩阵F的所有特征值。此时,maxθ∈ρ(Q)Reθ<0当且仅当F为正稳定矩阵即F的所有特征值都具有正实部。
证明 根据矩阵论知识可以得到det(θ I2n-Q)=,其中θ表示Q的特征值。
充分性:首先当θ=0时,根据Laplace定理可知det(F)=0而这与F为正稳定矩阵相矛盾。其次,当θ ≠0时,det(θ I2n-Q)=det(θ (θ +k) In+F)=0即-θ(θ +k)是矩阵F的特征值。不失一般性,假设-θ(θ +k)=μ(μ ∈ρ(F ))。令 θ=θ1+iθ2以及 μ=λ+iη,θ1,θ2,λ,η∈R,存在以下等式:

消去θ2,上式可化为:

由于 根据 Routh-Hurwitz定理知θ1<0 ,所以 maxθ∈ρ(Q)Reθ<0。
必要性:由于 maxθ∈ρ(Q)Reθ<0,对于式(10)根据韦达定理得可知λ>0即F为正稳定矩阵。
引理1[15]在拓扑图G中节点0全局可达当且仅当矩阵H=L+B正稳定。
定理2误差系统(5)在固定拓扑中渐近达到一致性的充分条件是:(1)通信拓扑中节点0全局可达;(2)控制参数k满足,其中 ρ()F表示n×n矩阵F的所有特征值。具体来说有:

4.2 固定时延编队控制分析
定理3控制协议(6)中的系统控制参数k满足k2>且存在常数

当 τr<τ0时误差系统(8)实现稳定即

的充分条件是通信拓扑图中的节点0全局可达。
证明 首先根据牛顿-莱布尼兹定理可得:

由于并且有:
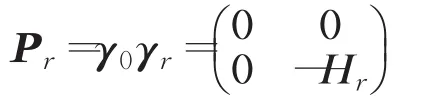
那么

其中
由Lyapunov定理[16]可知,存在正定矩阵W∈Rn×n满足

其中E为正定矩阵。
构造Lyapunov-Razumikhin函数为:

结合式(13),V()ε的导数可表达为:
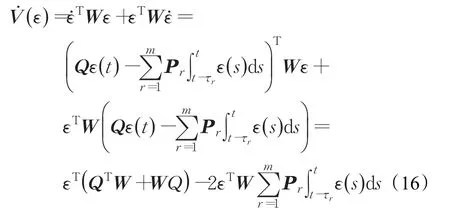
因为对于任意正定矩阵Φ以及列向量a和b都有±2aTb≤aTΦa+bTΦ-1b,所以式(15)可化作:
安全约束最优潮流的实用模型及故障态约束缩减方法//郭瑞鹏,边麟龙,宋少群,余秀月,汤伟,杨铖//(13):161

由Lyapunov定理[17]可知,当τ∈[- τ0,0] 时,V(ε (t +s))<φ(ε (t) ),令 φ(s)=αs(α >1),则有:

于是可得当:

则(V)
ε<0,由Lyapunov渐近稳定定理可知误差系统(8)实现稳定,定理3得证。
注3主要是对系统编队控制一致性进行分析。针对零时延情形,根据矩阵分析与Routh-Hurwitz定理,得到零时延误差系统稳定的k值范围与通信拓扑满足的条件。基于零时延情形的基本结论,构造Lyapunov-Razumikhin函数,分析得到固定时延误差系统渐近稳定的τr的范围。
5 仿真算例
主要对本文研究的理论结果进行仿真验证。通过MATLAB仿真,实现异构多机器人系统在领航跟随者模式下的编队控制。
5.1 参数初始化
将期望的编队队形设置为正方形,初始位置和速度见表1(随机设置)。异构编队系统的通信拓扑关系如图1。
那么,由其通信拓扑可知异构编队系统跟随者模型的Laplacian矩阵L为:

表1 参数设置

图1 通信拓扑

5.2 零时延编队仿真
基于5.1节的参数设置,并且设控制参数k=1,此时利用MATLAB进行仿真验证。
如图2~4所示,根据已推导得到的理论,系统中的0节点机器人全局可达且k=1,那么异构多机器人系统实现编队控制。仿真算例中,异构系统的各个机器人状态由图例对应表示,图2表示异构多机器人编队的运动轨迹,初始位置随机给出,当机器人运动时间超过15 s,位移超过2 m时,各个机器人到达表1所示期望相对位置,正方形队形逐渐形成,并在随后过程中保持编队队形。图3表示异构多机器人编队在x方向和y方向的位移变化,未形成编队前位移相差较大,15 s后逐渐达到期望位置。图4则表示了异构多机器人编队在x方向和y方向的速度变化,未形成编队时速度变化剧烈,15 s后各个机器人x方向和y方向的速度都趋于1 m/s,即速度亦趋于稳定、一致。

图2 异构编队系统的运动轨迹
5.3 固定时延编队仿真
基于5.1节的参数设置,并且设控制参数k=1.5,此时利用MATLAB进行仿真验证。
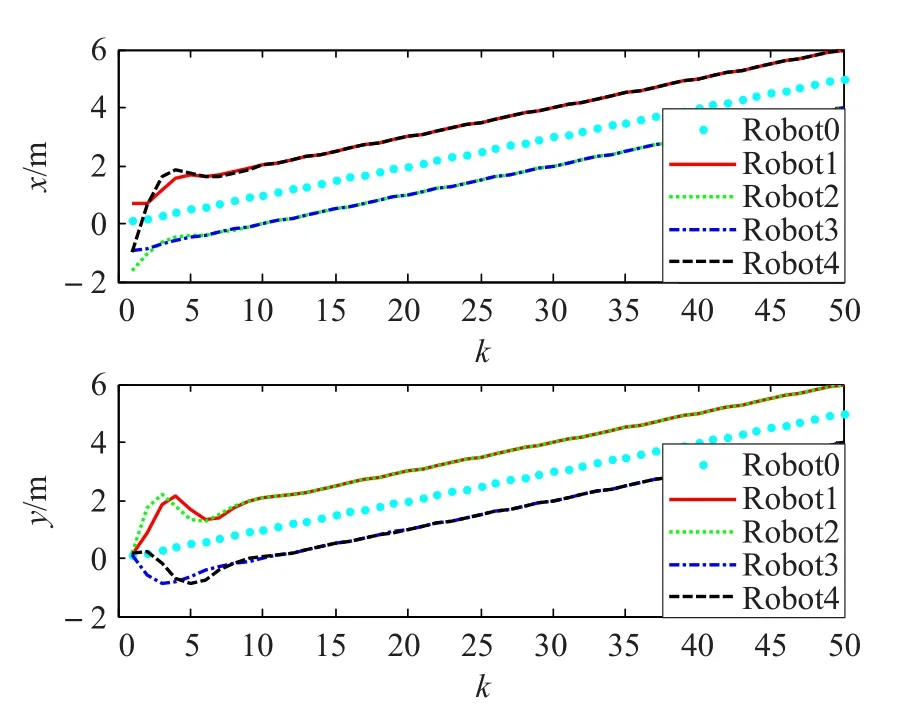
图3 x方向和y方向的位置变化曲线

图4 x方向和y方向的速度变化曲线
如图5~7所示,根据定理3可知时延上界为τ0=0.356,考虑选取 τ10=τ30=τ1=0.1,τ12=τ43=τ2=0.2,τ23=τ3=0.3,系统中的0节点机器人全局可达且控制参数k=1.5,此种情况下异构多机器人系统最终能够实现编队控制。仿真算例中,异构系统的各个机器人状态由图例对应表示,图5表示异构多机器人编队的运动轨迹,当机器人运动时间超过20 s,位移超过3.5 m时,各个机器人到达表1所示期望相对位置,正方形队形逐渐形成,并保持队形继续运动。图6表示机器人编队系统在x方向和y方向的位移变化情况,图7则表示机器人编队在x方向和y方向的速度变化,20 s后各个机器人的x方向和y方向的速度都趋于1 m/s,相较于图4可以发现,固定时延时机器人的速度前期变化更为剧烈,并且需要更多的时间实现稳定和一致。

图5 机器人编队系统的运动轨迹

图6 x方向和y方向的位置变化曲线
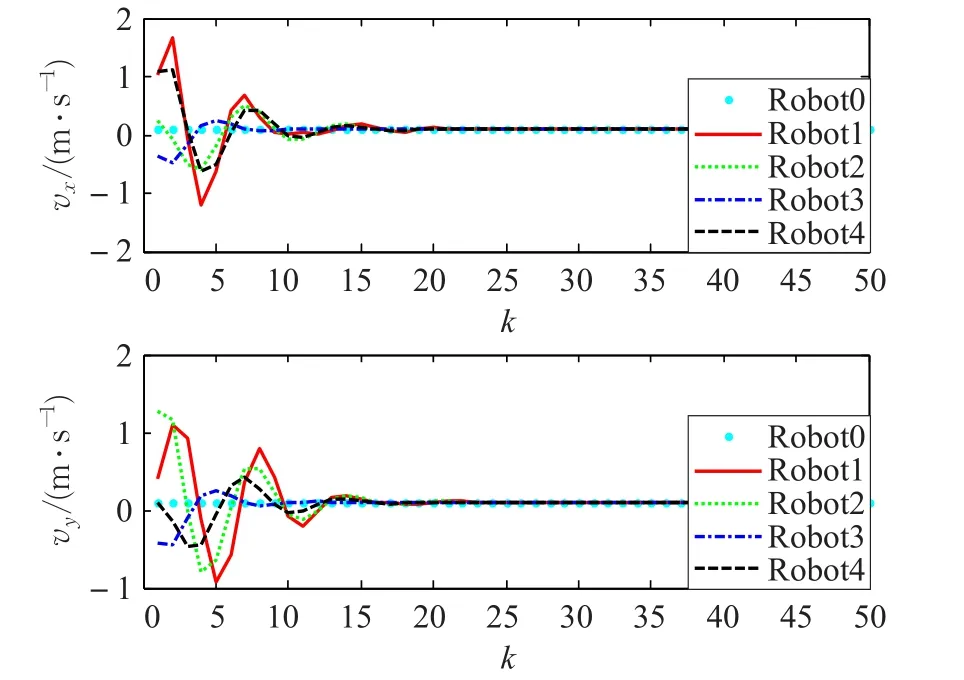
图7 x方向和y方向的速度变化曲线
6 结论
本文研究了异构多机器人系统相互通信时延的编队精确控制问题。首先,考虑零时延与固定时延两种情况,为降低同时对不同阶机器人进行编队控制一致性分析的难度,对领航跟随者模式的异构多机器人系统提出线性一致性控制协议。然后,根据矩阵分析与Routh-Hurwitz定理,得到零时延系统实现编队控制的充要条件。在此基础上,构造Lyapunov-Razumikhin函数,分析得到固定时延系统实现编队控制的充分条件。最后,通过两个仿真算例,表明本文所得结论的正确性和有效性。
[1]Li Z J,Li J X,Kang Y.Adaptive robust coordinated control of multiple mobile manipulators interacting with rigid environments[J].Acta Automatica Sinica,2010,46(12):2028-2034.
[2]Abdessameud A,Tayebi A.Formation control of VTOL unmanned aerial vehicles with communication delays[J].Acta Automatica Sinica,2011,47(11):2383-2394.
[3]Smith R S,Hadaegh F Y.Control of deep-space formationflying spacecraft relative sensing and switched information[J].Journal of Guidance,Control and Dynamics,2009,28(1):106-114.
[4]Jadbabaie A,Lin J,Morse A.Coordination of groups of mobile autonomous Agents using nearest neighbor rules[J].IEEE Transactions on Automatic Control,2003,48(6):988-1001.
[5]Jiang H,Yu J J,Zhou C.Consensus of multi-agent linear dynamic systems via impulsive control protocols[J].International Journal of Systems Science,2011,42(6):967-976.
[6]闵海波,刘源,王仕成,等.多个体协调控制问题综述[J].自动化学报,2012,38(10):1557-1570.
[7]王祥科,李迅,郑志强.多智能体系统编队控制相关问题研究综述[J].控制与决策,2013,28(11):1601-1613.
[8]Liu K,Xie G M,Wang L.Containment control for secondorder multi-agent systems with time-varying delays[J].System&Control Letters,2014:24-31.
[9]Zhong Z Z,Sun L,Wang J C,et al.Consensus for firstand second-order discrete-time multi-agent systems with delays based on model predictive control schemes[J].Circuits System Signal Process,2015,34(1):127-152.
[10]Xi J,Shi Z,Zhong Y.Consensus analysis and design for high-order linear swarm systems with time-varying delays[J].Physica A:Statistical Mechanics and its Applications,2011,390(23/24):4114-4123.
[11]Zheng Y,Zhu Y,Wang L.Consensus of heterogeneous multi-agent systems[J].IET Control Theory and Applications,2011,16(5):1881-1888.
[12]Kim J M,Park J B,Choi Y H.Leaderless and leaderfollowing consensus for heterogeneous multi-agent systems with random link failures[J].IET Control Theory and Applications,2014,8(1):51-60.
[13]Liu C,Liu F.Stationary consensus of heterogeneous multi-agent systems with bounded communication delays[J].Acta Automatica Sinica,2011,49(9):2130-2133.
[14]孙一杰,张国良,张胜修.一类异构多智能体系统一致性协议的收敛性分析[J].控制理论与应用,2011,31(11):1524-1529.
[15]Ghabcheloo R,Aguiar A,Pascoal A,et al.Synchronization in multi-agent systems with switching topologies and non-homogeneouscommunication delays[C]//Proceedings of IEEE International Conference on Decision and Control,2007.
[16]Xie T T,Liao X F,Li H Q.Leader-following consensus in second-order multi-agent systems with input time delay:An event-triggered sampling approach[J].Neurocomputing,2015,9(4):130-135.
[17]Horn R A,Johnson C R.Topics in matrix analysis[M].New York:Cambridge University,1994:37-44.
—— 瓮福集团PPA项目成为搅动市场的“鲶鱼”

