数字示波器大触发延迟时间的变频测量方法
梁志国, 杨仁福
(1.北京长城计量测试技术研究所 计量与校准技术重点实验室, 北京 100095;2.北京无线电计量测试研究所 计量与校准技术重点实验室, 北京 100854)
1 引 言
数字示波器的触发延迟是一项用途广泛的测量功能,尤其是在单次事件的捕获和时间差测量中,具有其它方法无可替代的地位与作用[1~6]。其所测量的时间差可以覆盖从纳秒量级直至几百秒之间的宽广范围。与其广泛应用不协调的是针对触发延迟时间计量校准所做的研究并不很多。文献[7]针对实际触发点与标称触发点之间的差异作了较详细的研究,包括触发电平误差、触发延迟误差、触发抖动等,文献[8,9]针对小于一个信号周期的小延迟时间的测量与不确定度进行了分析和研究。针对大触发延迟的精确测量,文献[10]提出了一种基于时间累积及量子化周期特征的单频率测量方法,可以实现任意触发延迟的精确测量。但该方法的不足之处,体现在需要将大触发延迟分割成众多小触发延迟的增量累加,因而大触发延迟时的测量工作量巨大。针对这一问题,本文提出一种变频率测量方法,试图以较小的工作量实现大触发延迟的精确测量。
2 测量原理
变频法测量数字示波器大触发延迟的基本思想,是基于直接用相位差法测量数字示波器的触发延迟τ时,所获得的时间差仅是大触发延迟中小于一个激励正弦波形周期T的部分延迟τ0,真正的大触发延迟τ是该部分时间差τ0迭加整数个正弦周期,即
τ=τ0+m·T
(1)
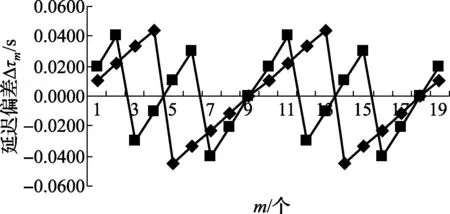
式中:m为非负整数,m=0, 1, 2, …,M,M为由延迟时间上限值和激励信号周期T确定的整数,即τ 由式(1)可见,在周期T(频率f=1/T)的正弦信号激励下获得时间差τ0后,可以判定其真正的大延迟时间一定是在式(1)所示的M+1个离散时间点上。 将激励正弦信号周期变化到Ta(频率fa=1/Ta)上,直接测量获得延迟时间差τa0,有 τ=τa0+k·Ta (2) 式中:k为非负整数,k=0, 1, 2, …,K,K为由延迟时间上限值和激励信号周期Ta确定的整数,即τ 若在上述式(1)所述的离散时间点上能够找到使式(2)成立的唯一点k所确定的τ值即为所求。 若k值不唯一,是由于K选取过大造成的。则通常这些不唯一的k值呈等差级数排列,其余的值均是最小的k值的整数倍,而最小的k值即为所求。 此时,需要将激励正弦信号周期调整到Tb(频率fb=1/Tb)上,直接测量获得延迟时间差τb0,有 τ=τb0+q·Tb (3) 式中:q为非负整数,q=0, 1, 2, …,Q,Q为由延迟时间上限值和激励信号周期Tb确定的整数,即τ 在上述式(1)、式(2)同时满足的离散点上寻找使式(3)成立的点q所确定的τ值即为所求。 若q仍然不唯一,则最小值点q所确定的τ值即为所求。具体过程如下: (1)如图1所示,根据被测量数字示波器触发信号的幅度范围和触发信号频率范围,选取正弦信号源的信号频率f,信号幅度,用三通将正弦波信号同时加载到数字示波器的测量通道和触发输入端。 设定被测量数字示波器的触发条件,令触发延迟为0,触发测量并记录采样波形序列,获得采样时间点t0,1,t0,2,…,t0,n上的等间隔采样序列为x0,1,x0,2,…,x0,n。 图1 触发延迟测量原理框图 用4参数正弦波拟合方法进行最小二乘波形拟合,其波形最小二乘拟合曲线的函数表达式为 (4) 拟合残差均方根值为 (5) (2)其它条件不变,设定触发延迟为τ,触发测量并记录采样波形序列,获得采样时间点t1,1,t1,2,…,t1,n上的等间隔采样序列为x1,1,x1,2,…,x1,n。 用4参数正弦波拟合方法进行最小二乘波形拟合[11],其波形最小二乘拟合曲线的函数表达式为 (6) 拟合残差均方根值为 (7) 则,直接测量获得的触发延迟τ0对应的相位差Δφ1可以表示为 Δφ1=2π·f·τ0=φ1-φ0 (8) (9) τ0与大触发延迟τ之间符合式(1)所述的量子化关系。 (3)其它条件不变,仅仅将激励正弦信号的周期变为Ta(频率fa=1/Ta)上,按照上述(1)~(2)所述过程直接测量获得延迟时间差τa0,则τa0与大触发延迟τ之间符合式(2)所述的量子化关系。 在式(1)所述的离散时间点上寻找使得式(2)成立的唯一k值点,其按式(2)所确定的τ值即为所求。 若k不唯一,则由于采样的周期性关系,后续的k值均应分别为第1个值的2、3、4、…倍数关系,由此判定最小的k值所确定的τ值即为所求。 继续变化正弦信号频率,在同时符合式(1)、式(2)要求的离散时间点上,重新寻找同时满足式(1)、式(2)、式(3)的唯一整数值点q,其按式(3)所确定的τ值即为所求。 若q不唯一,则由于采样的周期性关系,后续的q值均应分别为第1个值的2、3、4、…倍数关系,由此判定最小的q值所确定的τ值即为所求。 如图1所示接线。使用Agilent公司的DSO8104型数字示波器作为被测量仪器,其A/D位数为8 Bit,频带宽度1 GHz,存储深度为16 M,共有4个测量通道。使用其通道 3为测量通道。 设置其幅度量程为±1.2 V(300 mV/div),直流偏置offset=-2 mV,采集速率v=2 GSa/s(500 ns/div),通道采集数据个数n=20 022,触发电平202 mV, 上升沿触发,待测的触发延迟τ=1.1 s; 用HP公司的HP3325B合成信号源产生的正弦信号波形作为标准激励,激励正弦波形峰值幅度0.5 V,频率分别取为f=9.000 000 Hz,fa=10.000 000 Hz,fb=11.000 000 Hz。 则,通过执行上述过程,分别获得相对应的直接测量结果为 τ0=99.53 ms τa0=99.84 ms τb0=87.79 ms 设最大延迟时间值为2 s,则可得M=19,推定m=0, 1, 2, …, 19。 针对不同的m值,通过调整k值,使得式(2)和式(1)两者之差的绝对值最小的两个延迟偏差Δτm为 Δτma=τ0+m·T-τa0-k·Ta (10) 同理,针对不同的m值,通过调整q值,使得式(3)和式(1)两者之差的绝对值最小的两个延迟偏差Δτm为 Δτmb=τ0+m·T-τb0-q·Tb (11) 式(10)和式(11)所计算的延迟偏差曲线如图2所示。 图2 延迟偏差与周期数m的关系曲线 从图中可见,对于每个频率而言,获得的延迟偏差曲线为非均匀的锯齿波形状,具有近似的周期性,最小周期为公共近似“0”点。 通过对比两个序列最接近0值所对应的最小m值,即可判定其所对应的延迟时间差即为所求。 从图2可知,两条偏差曲线在m=9和m=18处最接近0值。 m=9时,有 Δτma=-0.3100634 ms; Δτmb=-0.1581907 ms m=18时,有 Δτma=-0.3099442 ms; Δτmb=-0.1580715 ms 尽管m=18时延迟偏差的绝对值较m=9时更小,但都属于在测量与计算误差的波动范围之内,可认为两者均符合式(2)要求,不能简单据以区分m点位置。 由于18是9的2倍,可以判定m=9取最小值即为所求。此时,由式(1)计算获得的触发延迟时间差为:τ=1.09953 s。 对于τ而言,由于将大延迟时间差分成整数个周期部分和小数个周期部分两部分组成,其整数个周期部分,时间量值为1 s,对于所用信号源,其周期相对误差为±2×10-6,因而其相对不确定度也为2×10-6量级,绝对不确定度在微秒量级。而小数个周期部分,时间量值为99.53 ms,其不确定度在亚毫秒量级,与小数个周期部分相比,本文中整数个周期部分的不确定度可以忽略。因而,使用本文上述方法,可以保证τ有5位有效数字。 直接使用相位差法进行触发延迟时间差的测量时,其不确定度评定可以参照文献[8]执行,本文不再赘述。获得的参考结论是,其通常仅有2~3位有效数字。 从上述过程可见,本文所述方法以3个不同频率上的延迟时间差的直接测量,经过一番运算和判定,可以实现大延迟时间差直接测量与校准。与此前的累积法相比,其实验工作量大幅降低,仅需要测量3组数据。但是,其比较运算的工作量仍然比较大,其与M值基本上成正比,这是本文方法的缺点。避免该缺点的方法主要有两点:一是尽量将触发延迟时间的估计上限不要太大,尽量低于实际值的2倍;二是选取尽量低的激励信号频率,由此导致M值较小,从而降低比较运算的工作量。 另外,本文方法的局限性还在于使用了式(2)和式(3)进行相等判定,以确定m、k、q等的取值,这在实际工作中是非常困难的。由于测量误差、运算误差等的存在,工程上真正的相等是很难出现的状况。需要预先估计方法本身的误差或不确定度,设置恰当阈值,当式(2)及式(3)所示时间差与式(1)所示时间差之间的差异小于设定阈值后,即初步认为该点可能符合要求,后续再通过符合要求的点具有周期性的特征,且不同频率下的周期性相同判定其m、k、q等的正确取值。 从式(10)和式(11)所述的延迟偏差曲线可见,每一个频率下的延迟偏差均是具有周期性的多齿形近似锯齿波形状,不同频率下的延迟偏差具有公共周期,其最小公共周期所确定的m即为所求的正确值。实际工作中需要据此特性在多值条件下判定正确的m值。 由于本文选取最大触发延迟时间为2 s,近似其标称值的2倍,因而出现了9和18两个符合要求的m值。实验已经证明,若选取更大的触发延迟范围极限时,m将在27、36、45、…、9n、…等后续9 的倍数处出现符合要求的情况。 另外需要注意的一点是,本文所述的大触发延迟,是与0触发延迟相比较而产生的增量延迟,并非是与定义触发点相比的绝对延迟,有关绝对延迟的测量实际上是要参照本文方法获得的延迟,结合0延迟时其实际相对于定义触发点的绝对延迟合成而得,相关文献给出了0延迟时其相对于定义触发点的绝对延迟的测量方法。 综上所述,本文所述方法主要是针对大触发延迟时间测量中该被测量的大延迟时间在与使用直接相位差测量法获得的时间差相比,一定相差整数个激励波形周期这一量子化特征,尝试以不同频率下的测量结果之间具有公共周期性这一本质特征寻找出其公共周期,从而实现大触发延迟中所包含的正弦信号周期个数m的正确判定。 然后,将m个周期所代表的时间差与用直接相位测量法获得的时间差相合成,最终获得数字示波器大触发延迟的测量结果。与累积法相比,该方法的实验工作量可以大大降低,但其计算工作量则大幅提高。 该方法可将触发延迟时间差溯源到激励正弦信号的频率量值上,无须使用外接硬件延时器,适合于计量部门和用户对数字示波器大触发延迟量值实现精确测量与校准。 [参考文献] [1] 冯为蕾,王福娟,曾万祺,等.应用于LIBS的CCD光谱测量系统[J].激光与光电子学进展,2013,50(1):013002-1-013002-7. [2] 梁境锋,李光灿,杜勇,等.TSA线性阵列的脉冲辐射特性分析[J].电子测量技术,2012,35(8):38-41. [3] 顾军.频率捷变信号源的捷变合成研究及实现[J].电子测量技术,2010,33(6):17-19. [4] 卫兵,卿燕玲,李洪涛,等.开关触发延迟时间和抖动测量的不确定度分析[J].强激光与粒子束,2010,22(7):1649-1652. [5] 程度,耿春萍,张治.逻辑分析仪在数字电路测试中的触发选择[J].现代电子技术,2007,30(13):160-162. [6] 武锦辉,李仰军,赵冬娥.激光测速靶连发弹丸速度测试系统[J].兵工自动化,2005,24(4):16-17. [7] 梁志国.数字存储示波器触发点电平和延迟的精确校准[J].仪器仪表学报,2011,32(6):1403-1409. [8] 梁志国,孟晓风.波形记录仪触发延迟的测量不确定度评定[J].计量学报,2011,32(4):361-367. [9] 梁志国,孟晓风.波形记录仪触发延迟线性的实验研究[J].计测技术,2009,29(5):4-7. [10] 梁志国.数字示波器大触发延迟时间的量子化测量方法[J].计量学报,2018,39(1):94-98. [11] 国家质量技术监督局. JJF1057-1998 数字存储示波器[S].1999.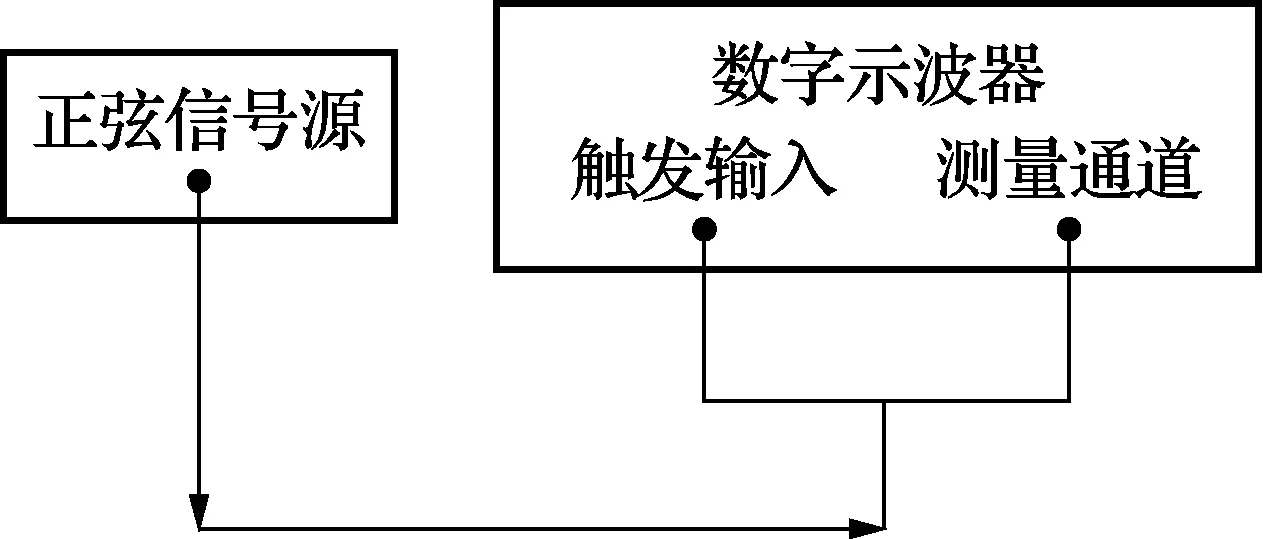
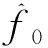
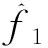
3 实验验证
4 不确定度分析
5 讨 论
6 结 论

