动力学有限元模型的复模态评估

余好文，王 轲

（南京航空航天大学 机械结构力学及控制国家重点实验室，南京 210016）

目前常用的结构动力学有限元模型评估方法主要适用于实模态情况下的模型评估，一般是从频率和振型两方面来评估所建立有限元模型的模态准确性，具体的方法是从试验所测得复模态中提取实模态的相关信息，然后与所建立的有限元模型计算结果比较。对于一个模型，即使经典评估方法的结果良好，用于响应计算可能仍具有较大误差。其产生误差的原因主要在于两方面，首先，经典方法评估结果多，难以整体把握模型；其次，振型MAC[1]评估并不能全方面反映各阶模态相位差的准确性，此外实际结构都是含有阻尼的，较大的阻尼对结构响应的影响是不可忽略的。

对于含有阻尼的结构系统，各自由度将在不同时刻到达平衡位置或最大值，复振型完备描述了各个自由度作纯模态振动时幅值间的比例关系和相对相位值，基于复模态理论[2]，本文提出了一种复模态下的频率和振型评估方法，该方法从复频率、振型幅值及振型相位值三个方面进行试验与数值计算结果的相关性评估。

首先，通过试验复频率和仿真复频率的相对误差求出复频率相关性系数，试验和仿真的复振型幅值相关性系数可通过模态置信度准则求出，而复振型相位值相关性系数可通过定义的矩阵范数求出。然后依据各类评估结果提出了一种综合评判方法[3]，该方法将复频率、振型幅值及振型相位值看做3个影响因素，首先通过各阶模态取不同权重形成每一个影响因素的评估结果，然后通过3个影响因素取不同权重形成最终的一个评估参数。本文最后通过一个算例，证明了复模态评估相对于经典方法在评价模型方面具有更好的可靠性，该方法以评估模型响应计算能力为目标，评估结果更能反映该模型优劣。

1 经典有限元模型评估

经典有限元模型评估方法通过计算频率相对误差和振型MAC矩阵来评估模型准确程度，两种方法定义如下：

同1阶模态的试验频率和仿真频率做比较，即为相对误差，可表示为

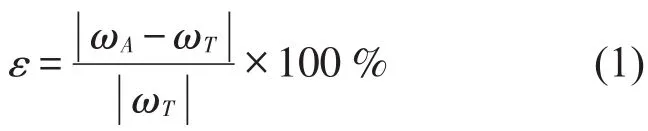
其中ωA表示有限元仿真的频率，ωT表示试验所测得的频率，ε的值在0～1之间，值越小表示两个频率越接近，该方法是非常常用的一种评估手段。

模态置信度准则（Modal Assurance Criteria，MAC），该方法定义为

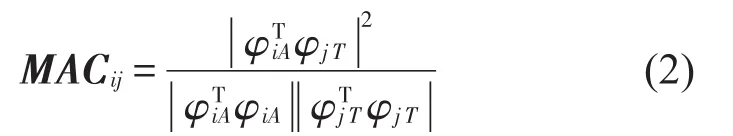
MAC矩阵中的每一个元素表示两个振型间的夹角余弦，MAC矩阵中非对角元素越小，各阶固有模态振型区别越明显，MAC矩阵中对角线元素越接近于1，表示试验和仿真分析模态相关性越高，在有限元模型中常常采用该方法评估振型的相关性。

上述两种评估方法存在一些不足，首先，频率评估结果为一个m×1的列向量，振型MAC评估结果为一个m×m的矩阵（m为模态阶数），此时评估参数多，并且不同模态相关性有好有坏，难以把握整个模型优劣；其次，MAC评估也只从振型幅值上评估，无法反映振型相位差异；对于一般模态试验测得的复模态，在实模态化过程中会形成二次误差。

2 复模态相关评估

一般黏性阻尼系统的振动微分方程为

得到二次特征值问题

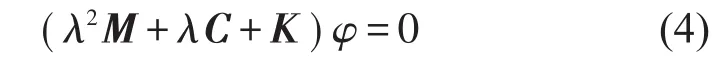
它具有非零解的充分必要条件是

该方程可解出2N个特征值λr以及2N个N维特征向量φr，由于上式是实系数代数方程，故复特征值和复特征向量必共轭成对出现，分别称为第r阶复频率和复振型。

复模态评估方法分为3个方面，复频率相关性分析、复振型幅值相关性分析及复振型相位值误差分析，前两者在取模或实数化后有较为成熟的评估方法，但相位相关性迄今没有合适的描述方法。

设有限元仿真复频率为λA，试验复频率为λT，则复频率相对误差定义为式（6）

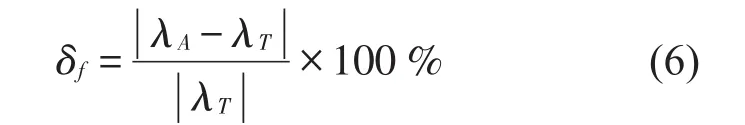
复频率相关性则可定义为式（7）

该方法为常用的频率相关性分析方法，只有λA和λT的实部和虚部对应接近相等时，相对误差δf才趋于零，复频率相关性Rf趋于1，该方法为各阶复频率单独评估，最终评估结果为m×1的列向量，m为评估模态阶数。

复振型的相关性若采用模态置信因子的共轭取模算法，其MAC矩阵为复振型的综合反映，无法单独体现幅值与相位值的误差情况，且模态置信因子对试验与仿真各自由度上相位值差异的灵敏度较低，但复振型相位值的误差对响应计算有较大影响。因此，为较全面反映复振型的误差情况，本研究将从幅值和相位值两方面来进行相关性分析，且该评估方法有明确的物理意义。

试验测得复振型和有限元仿真复振型分别为ΦT和ΦA，则其各点的相位值分别为

振型幅值为，其中相位大于零则取正，反之取负

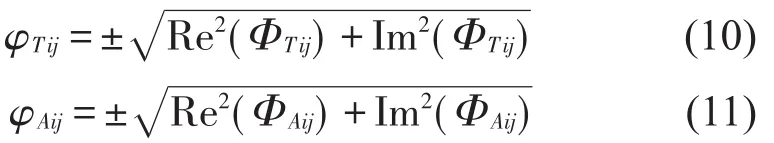
复振型幅值相关性分析可通过求模态置信度准则MAC。

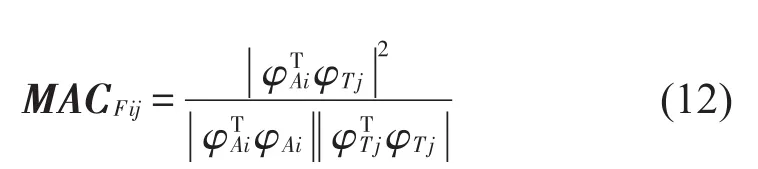
其中：φAi、φTj分别为上述所求得仿真第i阶、试验第j阶的复振型幅值。MAC值反映复复振型幅值的相关性大小，该方法最终评估结果为m×m矩阵，m为评估模态阶数，在进行综合评估时，取矩阵对角线元素作为相关性系数。

相位值误差分析可分为3部分，各自由度上的相位值误差分析、各阶模态误差分析及总体相位值误差分析。

各个自由度上的相位值相对误差Δθij可定义为

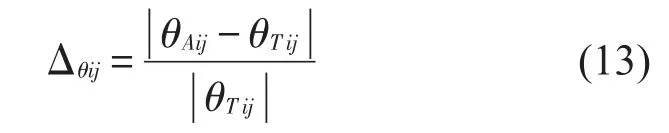
通过各个自由度相对误差矩阵Δθ，可判断该模型的相位值误差在各个自由度上的分布情况。

各阶模态相位值误差及总体相位值误差可通过求解相关矩阵范数来分析，首先定义一个矩阵范数‖.‖

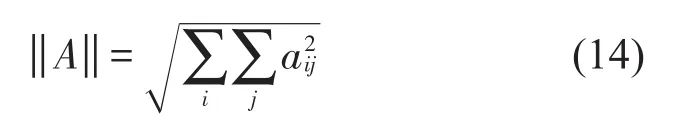
则各阶模态相位值相对误差定义为

各阶模态相位值相关性定义为

其中：θTi与θAi分比为试验和仿真第i阶复振型相位值，Rθ可评估每1阶模态相位值的相关性大小，相位值相关性评估结果为m×1矩阵，m为评估模态阶数。

总体相对误差ΔF定义为式（17）

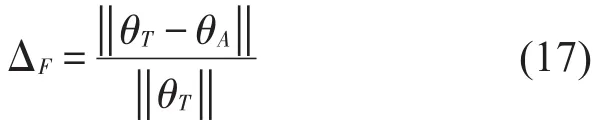
总体相对误差可定量评价总体振型相位值的误差大小，总体相对误差值越小，模型越好，该值可为比较不同模型之间的优劣提供数据支持。

复模态评估主要从3个方面来评价该模型的好坏，数据量众多，难以从整体上判断模型的好坏，或者说缺少一个具有特征指示意义的标量，现利用模糊理论[4]和层次分析法，以评估响应计算精度为目标，提出一种能综合衡量该模型的参数。

根据复频率、复振型幅值、复振型相位值3个影响因素可分为两个阶段的评估，第1阶段为复频率、复振型幅值、复振型相位值3个方面的单独评估，第2阶段为3个影响因素的综合评估，每1阶段评估的权重系数由层次分析法得到。

在第1阶段评估中，复频率、复振型幅值及复振型相位值相关性分析都是对m阶模态进行的，因此3个影响因素都包含m阶模态的影响，各个模态的权重系数可根据各阶模态对响应的影响来判定，对结构响应影响较大的模态其权重系数高。

各阶模态权重系数选取可根据频响函数固有频率处幅值来确定，由研究人员选取结构上比较重要或具有代表性的点，设结构上该点的频响函数固有频率处的幅值分别为a1、a2、…、am，其中m为模态阶数，设

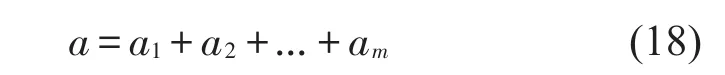
则各阶模态所构成的权重系数向量为

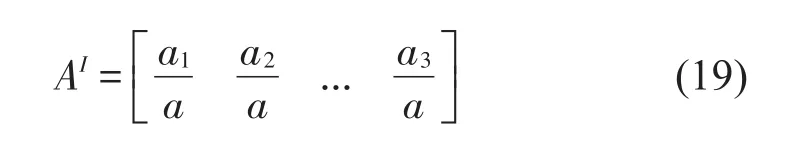
此为第1阶段的权重系数，3类影响因素选取相同的权重系数集AI；在第2阶段评估中，认为复振型幅值及相位值的影响略大于复频率的影响，则根据层次分析法求得3个影响因素的权重如表1所示。

表13类影响因素权重

则有第2阶段权重系数

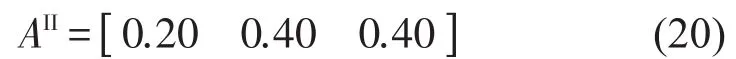
根据模糊评估理论，将评判结果设为5个等级：

{很好，好，一般，较差，很差}

模糊综合评判的目的就是在综合考虑上述3个影响因素的基础上，从评判结果选择最合适的结果。

为进行综合评估首先确定隶属度函数，隶属度函数是各个影响因素从属于上述5个评判结果的程度，本研究选择梯形隶属度函数r()x，如下式

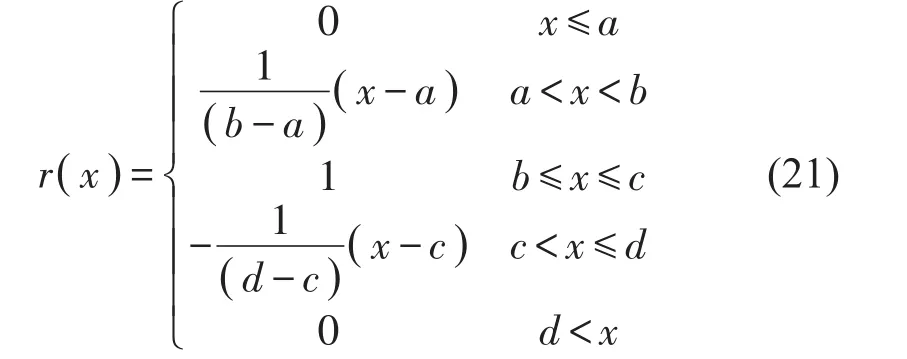
将式（21）用图1表示为

图15种评价结果隶属区间图

根据梯形隶属函数，可分别确定复频率模糊关系矩阵R1、复振型幅值模糊关系矩阵R2及复振型相位值模糊关系矩阵R3，即

在上式中：k=1,2,3，m为评估模态阶数。

在复频率模糊关系矩阵R1中某元素r1ij表示第i阶频率相关性系数在第j种评价结果的隶属度，复振型幅值模糊关系矩阵R2中某元素r2ij表示复振型幅值评估MAC矩阵中第i个对角线元素在第j种评价结果的隶属度，复振型相位值模糊关系矩阵R3中某元素r3ij表示第i阶复振型相位值相关性系数在第j种评价结果的隶属度。

则第1阶段的评估结果为

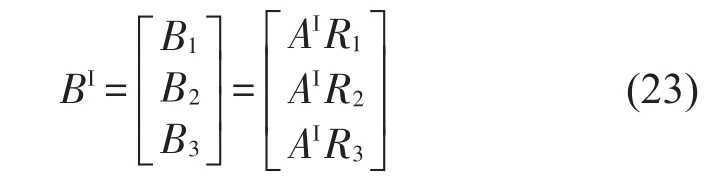
第2阶段评估结果为

第2阶段的评估结果BII为该模型综合评估结果在各个评价等级的隶属度，将5个评判等级量化，取量化参数C，即

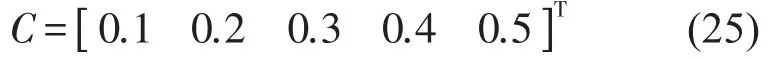
最终评估结果为

P值为0～1范围内的某一值，P值越接近1，模型越好，在整个评估过程中，各阶模态权重系数选择与对响应的贡献有关，并且复振型幅值和相位值权重系数较高，故该综合评估数值主要是反映模型响应求解精度的总体情况。

3 算例

某板结构如图2所示。

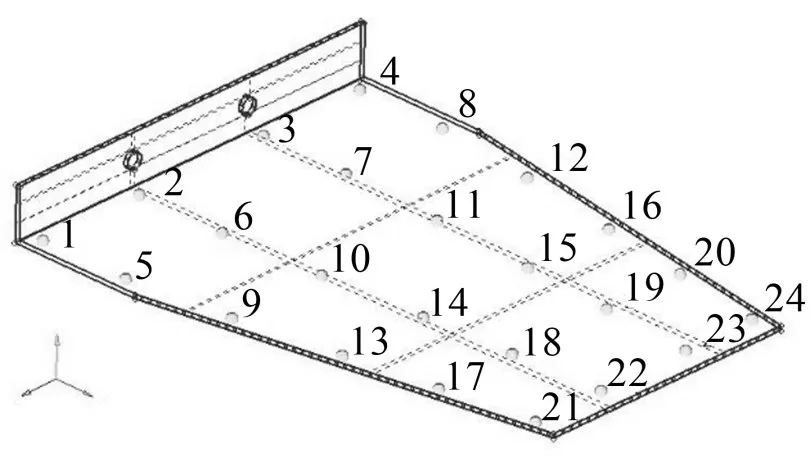
图2 黏弹性阻尼板

共有24个测量点，该结构底部粘贴有阻尼层，其运动特性受阻尼影响较大，试验测得其前4阶复模态，通过有限元建模仿真分析其前4阶复模态。

3.1 经典方法评估

首先通过经典评估方法评估该模型，在试验结果中提取实模态相关信息，评估结果如表2。

通过经典方法评估结果可以看出，该模型的每1阶频率和幅值相关性都很高，则根据该方法可认为该模型具有较高精度。

3.2 复模态评估

根据测得的试验结果，选择合适的阻尼模型，仿真时选用3参数阻尼模型[5]，复模态评估结果见表4和表5。

表2 频率相关性

表3 振型相关性

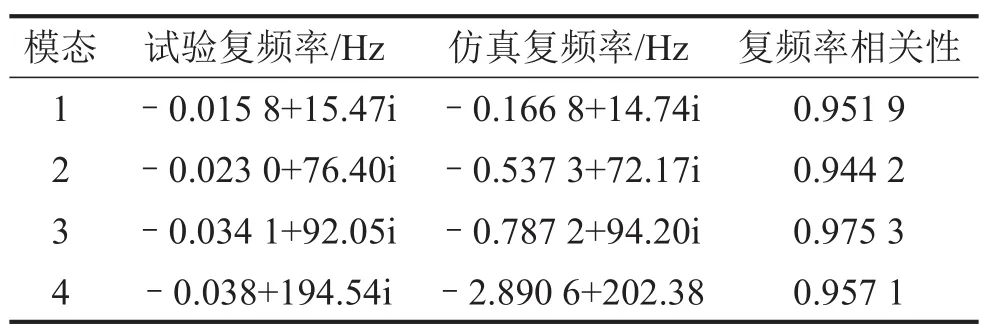
表4 复频率相关性

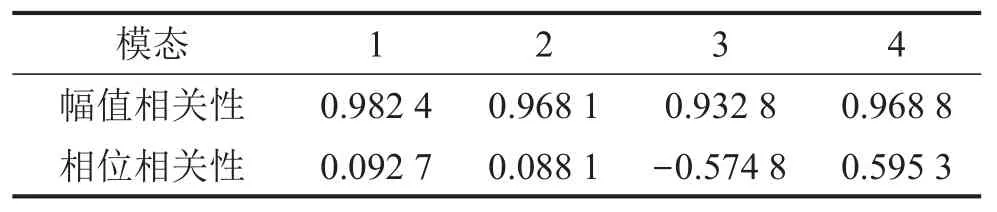
表5 复振型相关性

从复振型相位值评估结果来看来看，各阶模态相位值相关性不理想，误差的分布可通过计算各个自由度相位值误差得出。

在进行综合评估时，对该结构模型来说，低阶模态的影响应大于高阶模态，因此设定各阶模态的权重系数及3类影响因子的权重系数分别为

复频率影响因素隶属函数取值区间

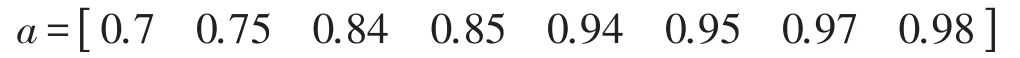
复振型幅值影响因素隶属函数取值区间

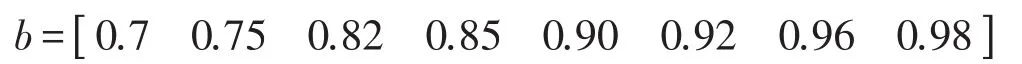
复振型相位值影响因素隶属函数取值区间

根据上述所求得3类因子的相关性系数，求得模糊关系矩阵R1、R2、R3

则第1阶段评估结果为

第2阶段评估结果为

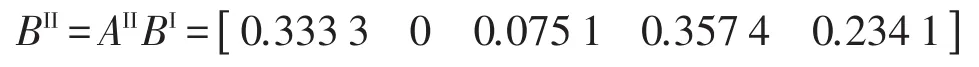
最终结果为

该模型综合评估结果为0.6318，处于一般水平，模型不是十分理想，其响应计算精度可能仍具有较大的误差，这与经典方法的评估结果不同，现通过响应计算分析其误差大小。

3.3 响应计算分析

经典评估方法认为该模型精度较高，从复模态综合评估方法可以看出，该模型响应计算方面并不具有较高的准确性，为验证两种方法的可靠性，现通过仿真与试验的响应结果来分析，激励点为10号点，对比24号点的响应，响应曲线见图3。

从计算结果可以看出，该模型响应计算误差较大，第1阶幅值误差甚至达到74.2%，复模态的评估结果能更准确反映该模型计算准确度，现通过相关模型修正[6–8]技术进行修正，修正后该模型复模态相关性如下表6。

修正后该模型综合评估结果为0.7064，响应曲线结果如图4，修正后该模型响应误差减小，第1阶幅值误差为20%，并且仿真与试验响应曲线更相近。

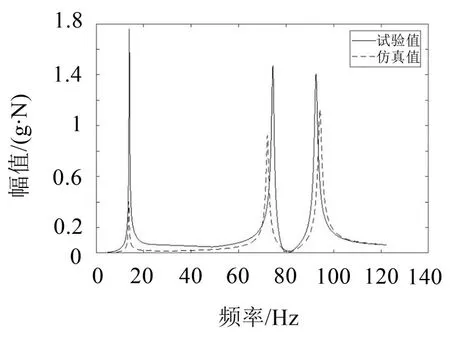
图3 修正前响应计算结果对比

图4 修正后模型响应计算结果对比

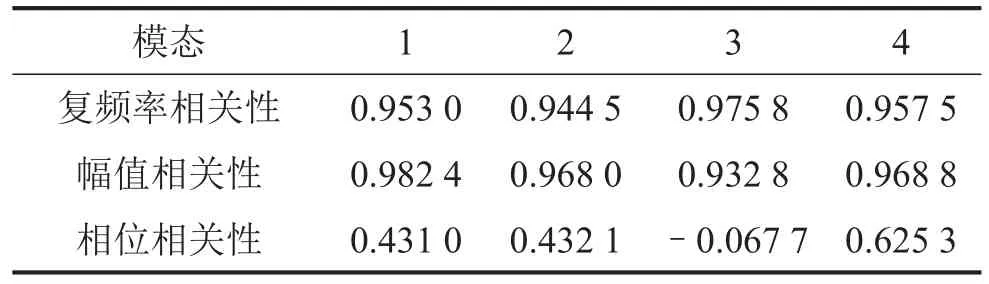
表6 修正后模型复模态相关性

综上所述，经典评估方法对于含阻尼结构模型的响应评估会产生较大误差，而复模态下的评估方法则能一定程度预估该模型响应计算的准确程度，可为最优模型的选择提供数据支持。

4 结语

进行模型评估的主要目的是选取能够反应结构动特性的最优模型，一般评估方法并未考虑阻尼对结构响应的影响，其选取出来的模型在进行响应计算时仍然具有较大误差。本文方法在复模态域内进行模型评估，通过复频率、复振型幅值及相位值三方的评估，可以很好反映阻尼所引起的模态相位值差异，并通过建立评判标准和权重集，将3个单方面的评估结果综合为一个整体的评估值，避免了多个参数评估的弊端。

本文算例表明该方法相比于传统方法，可较好地预估模型的响应准确度，为多个模型的筛选提供数据参考，该方法可广泛应用于含阻尼模型的评估及修正工作。

[1]MIROSLAVPASTOR,MICHALBINDA,TOMAS HARCARIK.Modalassurancecriterion[J].Procedia Engineering,2012,48:543-548.

[2]李德葆.关于复模态理论的数学方法、物理概念及其与实模态理论的统一性[J].清华大学学报(自然科学版)，1985(3)：26-38.

[3]张安平，王轲.动力学有限元模型的模糊评估[J].南京航空航天大学学报，2006(3)：367-372.

[4]李凡，耿旭，董效杰，等.多层次模糊算法在光电抗干扰性能综合评估中的应用[J].系统仿真学报，2015(9)：2176-2180+2186.

[5]王德鑫.基于频响函数的有限元模型修正及实验研究[D].南京：南京航空航天大学，2012.

[6]HUA-PING WAN,WEI-XIN REN.Parameter selection in finite-element-model updating by global sensitivity analysis using gaussian process metamodel[J].Journal of Structural Engineering,2015,141(6):1-11.

[7]ALTUNELFATIH,CELIKMEHMET,CALISKAN MEHMET.A Correlation improvement technique for model updating of structures[J].International Journal of Structural Stability&Dynamics,2016,16(8),1550049.

[8]MARCINLUCZAK,SIMONEMANZATO,BART PEETERS,et al.Updating finite element model of a wind turbine blade section using experimental modal analysis results[J].Shock and Vibration,2014.