障板对于平板声辐射特性的影响分析

刘 宝，王德石，朱拥勇

(海军工程大学 兵器系，武汉 430033)

工程实际中采用的许多结构可以近似看成为一个有限大的薄板，求解其辐射效率，声功率等声辐射特性受到了工程界的广泛关注。分析薄板的声辐射特性时，通常采用简支矩形板作为求解模型。不仅由于简支矩形薄板的振动模态表示简单，方便采用解析解表示其表面振速和声辐射特性参数，而且其解析解可以与数值计算方法如有限元法等做比较，揭示结构声辐射的一般规律。

早期研究简支矩形薄板的声辐射特性时，通常是将其置于无限大的障板上，这时只需要计算单层势，且积分项呈现弱奇异性，可以简化计算的复杂性。20世纪60年代，Maidanik首先提出了简支矩形板声辐射阻的近似方程，为后来的研究者提供了理论基础[1]。Wallace随后采用对远场声强进行积分，推导出了声辐射阻的一系列近似积分方程，成功求解出了吻合频率一下结构的模态声辐射功率[2]。Heckl在波数段内利用傅里叶变换研究分析了板的声辐射问题[3]，Leppington得出了几种近似方程求解大波数域振动模态辐射效率[4]。但是上述学者忽略了交叉模态对结构辐射声功率的影响。为此，Snyder和Tanaka利用模态辐射效率，考虑模态之间的耦合，计算出了低频时结构的辐射声功率[5]。Li和Gibeling采用积分变换的方法将结构的声辐射阻从四重积分形式转换为二重积分的形式，并成功的化为了一重积分的形式，求出了自辐射阻、互辐射阻及结构的辐射声功率[6–7]。对于水下平板的声辐射问题，由于需要考虑流体对结构的作用，因此可以归结为声振耦合问题。Crighton分析了点激励作用下无限大板在水中的声辐射[8–9]，Leibowitz提出了有限大板在水中声学特性的计算方法[10]。M.L.Rumerman研究了水荷载的存在对声辐射效率产生的影响[11]，B.E.Sandman进一步通过实验验证了求解流体载荷作用下板振动和声辐射问题的理论的正确性[12]。

然而在实际的工程当中，无限大的障板是不存在的，因此需要研究无障薄板的声辐射特性。Williams采用快速傅里叶变换（FFT），由迭代运算给出了简支无障薄板在空气中的声压，然而在计算高阶模态的声辐射阻抗时收敛性较差[13]。Atalla等采用Kirchhoff-Helmholtz积分方程计算了空气中任意边界条件下无障板的声辐射特性参数，然而在计算声压时忽略了平板两侧压力脉动的影响，在高频计算中误差较大[14]。Oppenheimer和Dubrowsky利用实验对有障薄板的声辐射参数修正，给出了计算无障薄板声辐射的经验公式[15]。

本文分析比较有障板和无障板的声辐射特性，由边界积分方程，分别推导有障板和无障板的声压积分方程，根据交界相容性条件，获取二重积分形式的平板表面声压和振速。进一步将结构的动力方程代入有障板和无障板形式的振速方程中，离散声压差值和板的位移为振动模态叠加的形式，获得二重积分形式的声辐射阻抗，从而求解振动模态系数，确定声辐射特性参数。以水下简支矩形板为例计算对比了声辐射参数，分析障板对薄板声辐射特性的影响。

1 平板动力学与声学基本方程

本文研究简支矩形薄板的声辐射特性。设板的密度为ρs，它长度分别为a、b，板的中心面与z=0平齐。有一个垂直于板面的激励力F(x,y)施加于上面，简谐角频率为ω，模型如图1所示。则由经典动力学可知，薄板的横向振动方程为

式中：B=Eh3/12(1-v2)为板的弯曲刚度，E为板的弹性模量，ν为板的泊松比。ˉ=ρsh表示板单位面积的质量。w(x,y)是板的横向位移。

图1 简支矩形板及坐标系示意图

简支矩形板的位移可以表示为如下振动模态的叠加

式中：Amn是振动模态系数，φmn(x,y)是模态形函数，表 示 为φmn(x,y)=sin(mπx a)sin(nπy b) 。 令Lm=mπ/a，Ln=nπ/b，则φmn(x,y)=sin(Lmx)sin(Lny)。

同样，外力也可以表示为如下形式

式中：Fmn为相应于模态函数φmn(x,y)的幅值。Δp(x,y)表示板上下表面产生的声压差值，可以表示为(x,y)为作用于薄板下表面的声压，p+(x,y)为作用于薄板上表面的声压。

平板在介质中的声压满足经典的Helmholtz积分方程，表示为

式中：p(x,y)为介质中任一点处的声压，k为波数，k=ω/c，c为声速，∇2为Laplace算子。

由Euler方程，交界相容性条件为

式中：ρf为介质的密度。

应用Kirchhoff-Helmholtz积分公式到一个包围板结构的无限大空间中，空间任一点M0的声压可以表示为

式中：C(M0)为声压系数，当M0位于结构外部空间取1，当M0位于光滑结构表面取12。分别称等号右侧第一项和第二项为单层势和双层势。nM表示结构表面的外法线方向，G(M,M0)为自由空间的格林函数，满足如下方程

式中：δ为Delta函数，(x,y,z)为M点坐标，(x0,y0,z0)为M0点坐标。G(M,M0)为自由空间的格林函数，表示为

式 中 ：表 示 空 间 一 点(x′,y′,z′)到板面一点(x,y,z)的距离。对上式进行二维Fourier积分变换，格林函数的另一种可以表达式为

式中：kx、ky是二维波数空间中的Fourier变量，。为了保证当 ||z-z0趋近于无穷时，格林函数G(M,M0)为有限数值，kz取为如下的形式

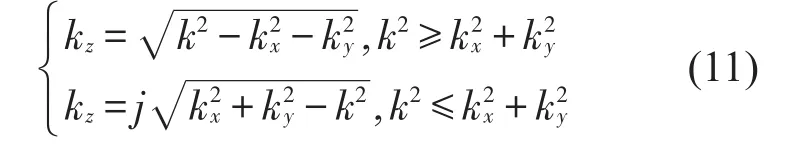
薄板上下表面法线方向相反，为此统一格林函数偏导方向为z轴正方向。由于声源位于结构表面，表面积分方程变为对Sl的积分（Sl为全部的S+和S-），如图2所示。

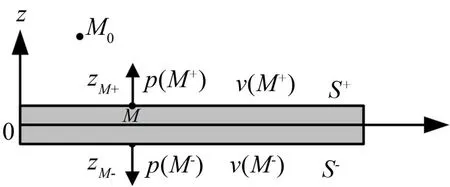
图2 简支板横截面图

2 有障板声辐射计算方程

对于有障板来说，由于(7)式中∂G∂nM为0，板结构上方一点r处产生的声压等于板面所有点对该点声压贡献的积分，从而式(7)可以化为

式中表示空间一点(x′,y′,z′)到板面一点(x,y,z)的距离。将式(12)代入式(1)，可得

由式(2)可知，矩形板的的挠度w可以表示为振动模态的线性叠加的形式，则代入式(13)可得

从式(14)可以看出每一个振动模态都会引起表面的压强变化。对式(14)在板面上进行Fourier逆变换，可得

式中：L2mn=L2m+L2n。

Zpqmn被定义为(pq,mn)阶声辐射阻抗。通过坐标变换令可以转化为二重积分形式，表示为

由坐标变换，可以方便地转化声辐射阻抗为二重积分的形式，将变换后的声辐射阻抗代入式(15)，表示成矩阵形式为

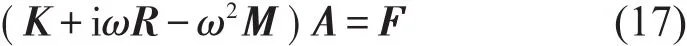
式中：K为刚度矩阵，，R为阻抗矩阵，矩阵中的每一个元素为Rpqmn=4 iωρfcZpqmn，M为质 量 矩 阵 ，，F为 外 力 列

由于上述矩阵中的质量矩阵，刚度矩阵已知，声辐射矩阵可以通过二重积分运算获得，则通过矩阵的求逆运算就可以获得振动模态系数矩阵A，进而可以求解板结构在重介质中的表面振速、声辐射功率等问题。

3 无障板声辐射计算方程

为了计算空间一点M0点处的声压，M0点的位置需要确定，式(10)中的格林函数可以表示为

则对于空间中任一点M0，式(7)可以离散为

式中：S+、p(M+)、v(M+)表示板上表面及其表面一点M+处的声压和振速，S-、p(M-)、v(M-)表示板下表面及其表面一点M-处的声压和振速。当板面很薄时，单层势项消失，即

且薄板中，近似看作相同，式(19)可以化为

式中：M为板表面任一点，(M,M0)表示沿z轴正方向进行的偏导。将式(1)代入式(21)，可得M0处的声压表达式为

由Euler公式，对式(22)两边在板面上求偏导，可得

式(23)建立了关于板表面位移w(x,y)的求解方程。对位移项w(x,y)，外力F进行振动模态展开，可得

对于作用于点(x0,y0)的点力F，Fmn可以表示为

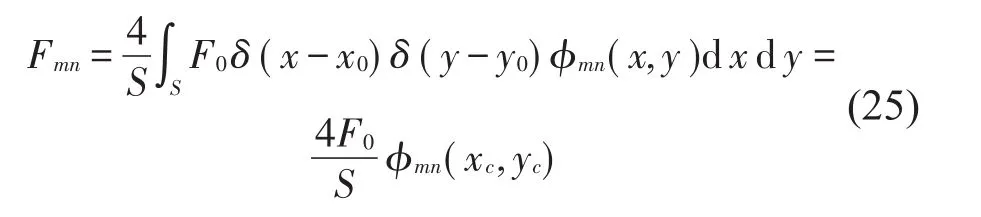
式中：F0为点力的幅值。

由振动模态的正交性，式(24)可以化简为

式中：，表示简支矩形板第(m,n)阶固有角频率的平方。系数交换格林函数与结构表面积分的顺序，可以将βpqmn表示为

式中：∗pq为pq的共轭复数形式的 Fourier变换，可以表示为

当m、p同为奇数或偶数并且n、q同为奇数或偶数时，βpqmn不等于零，否则为零。利用被积函数积分的对称性，进一步化简可得βpqmn可以化为如下形式

当确定了βpqmn元素后，Amn可以利用式(26)求解，矩阵形式表示为为

式中：β为βpqmn所形成的矩阵，Ω矩阵表示为

参考上节有障板声辐射计算方程中对于声辐射阻抗的定义，则无障板的声辐射阻抗表示为

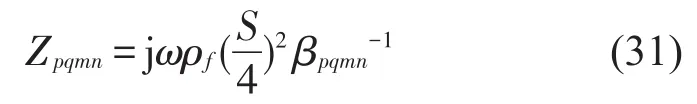
4 数值分析

平板产生的辐射声功率可以表示为

式中：Re表示复数的实部，v*为v的共轭复数形式。

将声压差值Δp，振速v*进行振动模态展开，可知

表面均方振速v2和声辐射效率σ分别表示为

设板长为a=1 m，宽为b=1.2 m，板厚h为级和均方振速级均取为10-12。0.01 m，水中声速为c=1400 m/s，不考虑板阻尼，参考声功率Wf=10-12W。在平板中心处处受到一个法向激励力作用，幅值为1 N。图3－图5分别为薄板声辐射功率，均方振速和声辐射效率的比较图，参考声功率

图3 平板声功率级比较

图4 平板均方振速级比较

图5 薄板辐射效率比较

由图3可知，障板的存在导致声辐射阻抗不同，从而引起了结构的共振频率发生改变，障板的存在导致结构的共振频率进一步降低，且引起结构的声辐射功率增加。这是由于障板存在时，平板由于表面振动压缩一侧的介质不能向另一侧稀疏态的介质流动，致使结构振动产生的能量更有效地转化为声能，从而增加了声辐射的能量，因此在相同频率下，有障板的辐射功率和效率都高于无障板的辐射功率和效率。有障板的辐射类似于单极子的声辐射，而无障板的声辐射则类似于偶极子产生的辐射。有障板的声辐射阻抗要高于无障板，声辐射抗相当于在结构表面附加质量，因此从图4中可以看出，总体上有障板的均方振速要低于无障板的均方振速。

5 结语

由平板模型，采用边界积分方程分别建立了有障板和无障板的声辐射计算公式，分析了它们各自的声辐射阻抗，并比较了有障板和无障板的辐射声功率，辐射效率和均方振速。从而可以得出：

(1)障板的存在致使结构的声辐射功率和效率得到提高，类似于将结构的偶极子辐射转换为了单极子辐射

(2)障板的存在也改变了结构在重介质中的共振频率，致使结构的共振频率降低。

(3)总体而言，有障板的均方振速要低于无障板的均方振速。

[1]MAIDANIK G.Response of ribbed panels to reverberant acoustic fields[J].Journal of the Acoustical Society of America,1962,34(6):809-826.

[2]WALLACE C E.Radiation resistance of a rectangular panel[J].Journal of the Acoustical Society of America，1972,51(3):946-952.

[3]HECKL M.Radiation from plane sound sources[J].Acustica,1977(37):155-166.

[4]LEPPINGTON F G,BROADBENT E G,HERON K H.Acoustic radiation from rectangular panels with constrained edges[J].ProceedingsofRoyalSociety LondonA,1984,393:67-84．

[5]SYDER S,TANAKA N.Calculating total acoustic power output using modal radiation efficiencies[J].Journal of theAcoustical Society ofAmerica,1995,97:1702-1709.

[6]LI W L,GIBELING H J.Determination of the mutual radiation resistances of a rectangular plate and their impact on the radiated sound power[J].Journal of Sound and Vibration,2000,229(5):1213-1233.

[7]Li W L,Gibeling H J.An analytical solution for the self and mutual radiation resistance efficiency[J].Journal of Sound and Vibration,2001,245(1):1-16.

[8]Crighton D G．Force and moment admittance of plates under arbitrary fluid loading[J].Journal of Sound and Vibration,1972,20:209-218.

[9]CRIGHTON D G.Approximations to the admittances and free wavenumbers of fluid-loaded panels[J].Journal of Sound and Vibration,1980,68:15-33.

[10]LEIBOWITZ R C.Methods for computing fluid loading and the vibratory response of fluid-loaded finite rectangular plates subject to turbulence excitation-option[R].NSRDC Rep,1971,2976C.

[11]RUMERMAN M L.The effect of loading on radiation efficiency[J].Journal of the Acoustical Society of America,2002,111(1):75-79.

[12]SANDMAN B E.Fluid-loaded vibration of an elastic plate carrying a concentrated mass[J].Journal of the Acoustical Society ofAmerica,1977,61(6):1503-1510.

[13]WILLIAMS E G.Numerical evaluation of the radiation from unbaffled,finite plates using the FFT[J].Journal of theAcoustical Society ofAmerica,1983,74(1):343-347.

[14]ATALLA N,NICOLAS J,GAUTHIER C.Acoustic radiation of an unbaffled vibrating plate with general elastic boundary conditions[J].Journal of the Acoustical Society ofAmerica,1996,99(3):1484-1494.

[15]OPPENHEIMER C H,DUBROWSKY S.A radiation efficiency for unbaffled plates with experimental validation[J].Journal of the Acoustical Society of America,1997,199(3):473-489.