陷波滤波器谐振抑制参数优化方法
李文涛,白瑞林,朱渊渤
(1.江南大学 轻工过程先进控制教育部重点实验室,江苏 无锡 2141222.无锡信捷电气股份有限公司,江苏 无锡 214072)
伺服驱动系统的机械传动装置大部分是存在一定弹性,通常会引发机械谐振。如果不对谐振进行抑制或谐振抑制不当,谐振不但会带来声学污染,而且还会造成机械装置严重损害[1]。目前伺服系统的速度环大多采用PI控制,而提高控制器增益经常会带来谐振,影响伺服的性能[2]。因此机械谐振的研究及抑制已经成为提高伺服系统性能的一个重要课题。
伺服驱动系统主要有两大谐振抑制方法,即主动抑制和被动抑制。主动抑制方式主要是改变控制器的结构或改变控制器的参数。被动抑制方式是在速度环和电流环之间插入滤波器,控制系统的结构不变[3]。目前工业伺服驱动系统主要采用陷波滤波器的方法[4]。文献[4]提出了自适应陷波滤波器的设计方案,可以快速地获取谐振频率并匹配陷波参数,消除谐振频率变化而使谐振抑制失效的问题。文献[5]针对谐振频率会随着环境和时间变化,设计了自适应IIR滤波器,通过最小二乘递推算法对谐振频率进行实时估计,该方法可以提高频率的估算精度。文献[6]对速度偏差做FFT变换和谐振定量分析来确定陷波滤波器的频率。上述方案中滤波宽度和深度参数都采用估计值,难以保证参数的合理性。
为了确定陷波滤波器的宽度和深度参数,文献[7]对滤波器设定了4个不同的零极点,利用循环查找的方法来确定谐振宽度和深度参数,该方法极点数目少,并不能确定最优参数值。文献[8]提出自适应陷波滤波方案,陷波深度用一个比较小的经验值。文献[9]在一个阈值内对每次匹配的滤波参数做FFT变换,虽然可以获得阈值内幅值最小的参数,但并不能保证参数最优。
本文在分析了不同弹性系数幅频特性的基础上,提出一种机械谐振抑制的参数优化方法。该方法利用改进型粒子群寻优算法对深度和宽度参数进行优化;并将控制效果和离线设置参数进行比较,实验结果表明该方法可以大幅度抑制机械谐振。
1 机械谐振的建模与分析
1.1 机械谐振的建模
在实际系统中,传动装置大部分是存在弹性的,并且每个装置都有固有的谐振频率。由电机、传动机构、执行机构组成的双惯量系统如图1所示。
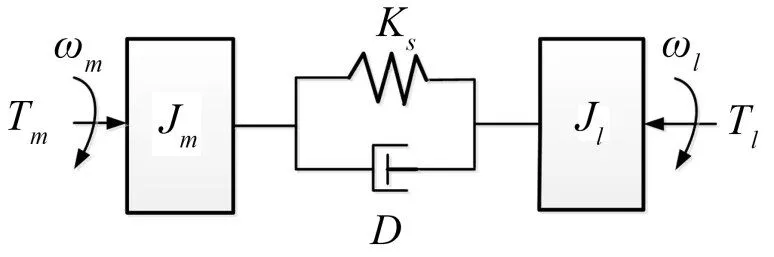
图1 典型双惯量系统结构图
电机和执行机构通过传动机构联接,传动机构的轴系具有一定的弹性Ks和阻尼系数D。当传动机构发生扭转变形时将产生轴系转矩Ts,此转矩对电机侧可看作是负载转矩,而对执行机构可看作是驱动转矩。伺服驱动器提供的电磁转矩Te和轴系转矩Ts共同作用于转动惯量为Jm、阻尼系数为C1的电机转轴。在负载侧,执行机构具有阻尼系数C2以及等效转动惯量Jl。轴系转矩Ts与负载转矩Tl共同作用,最终决定负载转速。根据上述分析建立如下微分方程组
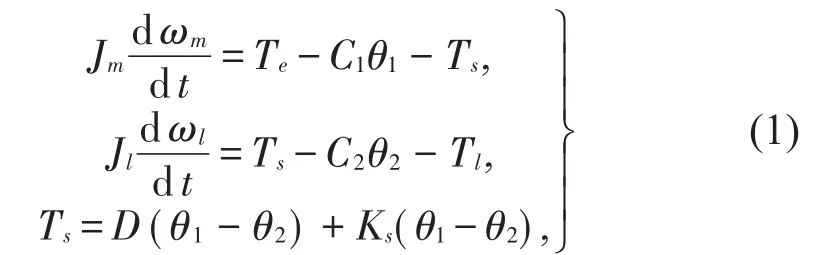
其中:θ1,θ2为

对公式(1)和式(2)做拉普拉斯变换得
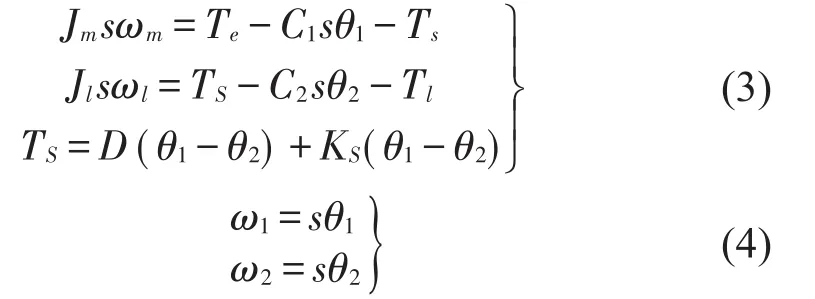
系统中的阻尼系数很小,可忽略从而对系统模型进行简化。根据公式(3)得电机速度与电磁转矩之间的传递函数。
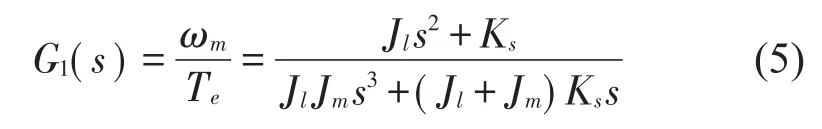
由式(5)得到图2所示的伯德图,从图中可以看出其幅频特性有一个幅值较高的谐振点和一个幅值较低的反谐振点。
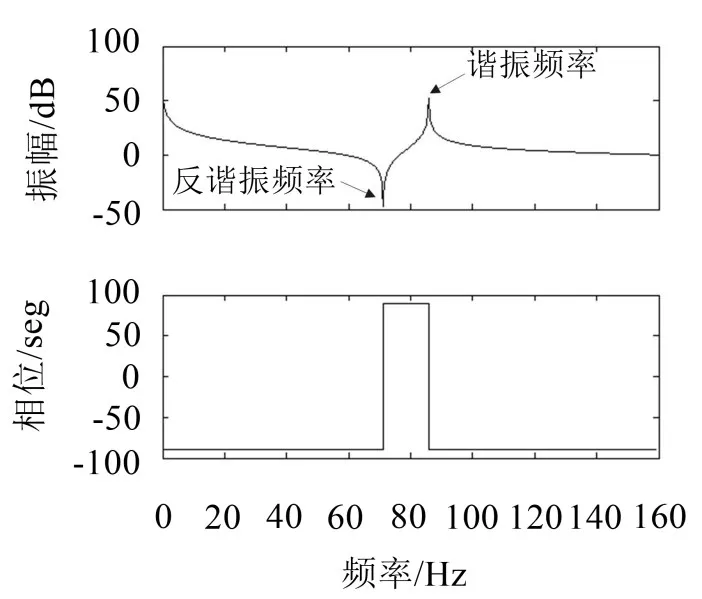
图2 双惯量系统伯德图
因此当电流的振荡频率或速度的振荡频率与谐振频率相等时会发生共振现象,造成设备严重损害。
1.2 机械谐振的影响
在伺服系统中,速度环采用PI控制器,其传递函数如式(6)所示。图3为Kp=0.1,KI=12.5,速度给定为ωc=3000 rad/s时的速度响应曲线。从速度曲线看出,响应在3000 rad/s持续振荡。如果电机持续在这种情况下运行将会降低机械寿命。

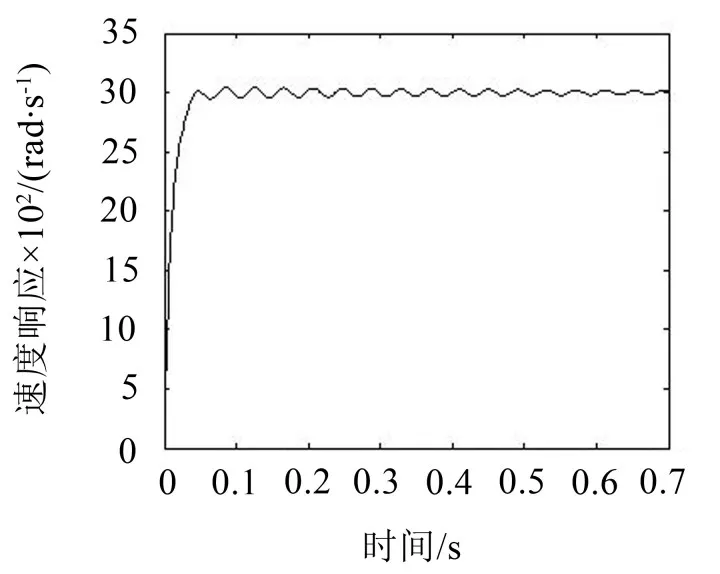
图3 电机速度响应曲线
2 机械谐振抑制及参数确定
2.1 陷波滤波器分析
为了能方便地调节滤波器的宽度和深度参数,选用双T型滤波器。双T型滤波器的传递函数为

f为陷波中心频率,ζ为陷波深度参数,K为陷波宽度。
设置陷波滤波器参数时,过大的陷波深度和陷波宽度将会导致在频率f的附近发生相角的超前或滞后,因此应该选择合适的滤波参数。
2.2 陷波参数的确定
(1)中心频率f的确定方法
陷波滤波器的中心频率点即为频谱图中对应的幅值最大的位置所对应的频率点,在中心频率点处滤波器提供最大的陷波幅值。图4所示的频谱特性曲线f即为陷波频率。
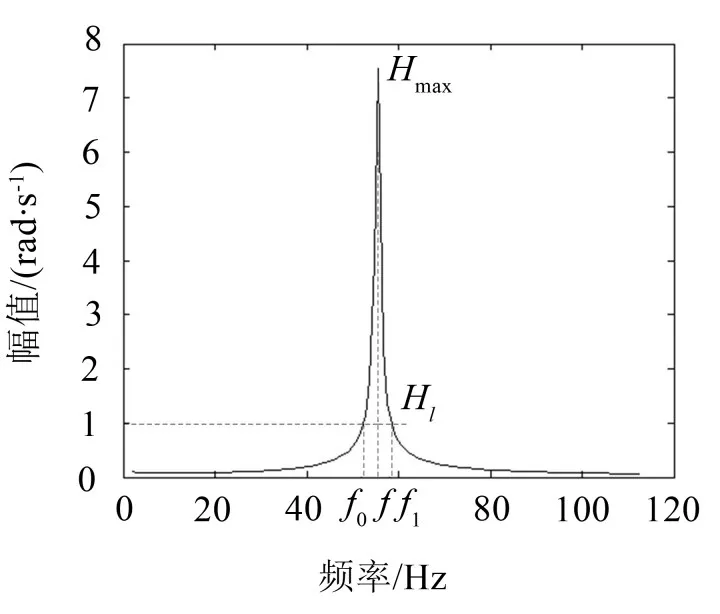
图4 谐振频谱图
(2)宽度参数k的确定方法
陷波滤波器宽度的确定是在频谱图上做水平线如图4所示,水平线将会与频谱图有两个交点,一个频率为f0,另一个频率为f1。在一般情况下f0与f,f1与f所确定的宽度并不相同。因此为了能更好的抑制机械谐振,陷波滤波器的宽度k取为f-f0与f1-f最大值的2倍。即

(3)深度参数ζ的确定
深度参数ζ表示在陷波中心频率点处所提供的最大幅值衰减,经过FFT之后,可以通过式(9)来确定陷波深度,其中Hl是陷波之后的幅度值。

此时陷波的深度表示为式(10)所示。

3 机械谐振频率辨识
为了获取谐振特性,本文将研究基于频率抽取的FFT算法,通过蝶形运算原理,实现频率抽取快速傅里叶变换,完成信号分析。对于数字控制系统首先采样一段有限长序列的数据x[n]。下式分别是傅里叶变换x[k]和反变换x[n]。
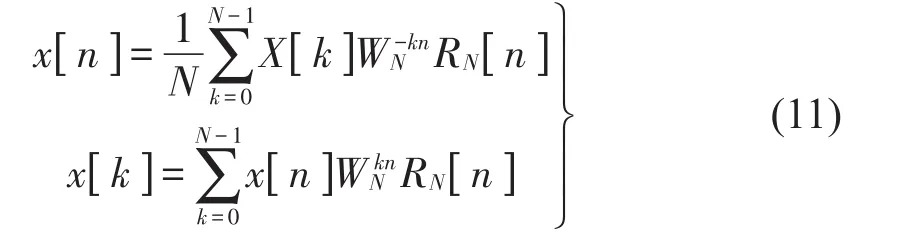
其中:WknN为旋转因子,RN[n]如式(13)所示。
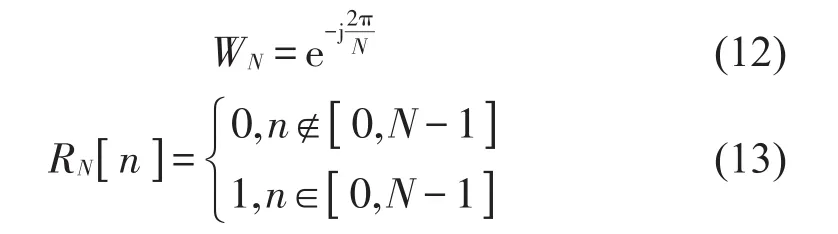
基于上式可推导出离散傅里叶变换公式
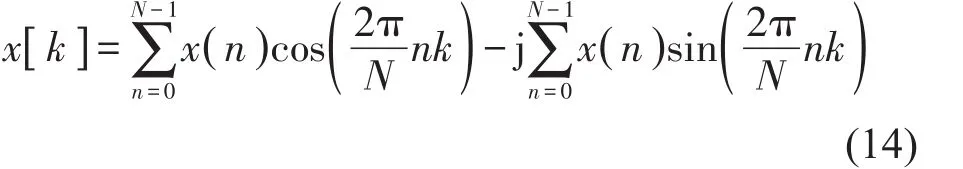
在FFT变换的过程中输入的是自然序输出倒位序,因此要将得到的序列按顺序放置。根据香农采样定理,连续信号的最高频率为fmax,为了使FFT之后的信号不发生混叠,采样频率满足fS≥2fmax。对于时域的采样频率fs,频域中的采样间隔F0满足如下关系N=f0/F0,因此在实际的应用中要考虑到采样点数和频率分辨率。
永磁同步电机采用磁场定向,在矢量控制中把电机的定子电流转化为旋转坐标系的直轴分量和交轴分量,直轴分量主要是来给电机励磁而交轴分量主要是用来产生电磁转矩。通过对电机定子进行解耦之后,电机的电磁转矩和交轴电流呈线性关系。当产生机械谐振时,电磁转矩将会持续振荡,最终会变为电机的速度振荡。机械谐振抑制的框图如图5所示。

图5 机械谐振抑制框图
在图中参数匹配策略在速度环中并不是一直运行的,而是开启之前首先要检测一段速度偏差的振动情况以避免干扰而引起误动作,对匹配的参数采用中断方式计算FFT,并利用寻优算法匹配最优参数。整个参数匹配策略步骤如下:
(1)利用速度偏差数据做FFT变换得到谐振频谱图。
(2)根据频谱图确定滤波参数。
(3)利用陷波滤波器对速度偏差进行滤波。
(4)利用下述算法对宽度和深度参数进行优化。
4 参数优化
4.1 优化分析
图6所示是在弹性系数发生变化时,匹配不同的深度参数后FFT的最大幅值;从图中可以看出弹性系数变化时,也会存在一个最小的幅值。
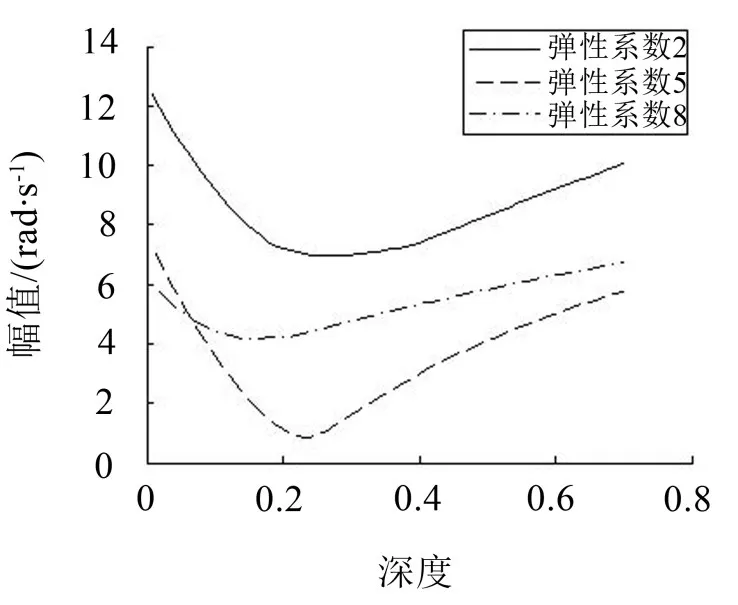
图6 不同弹性系数的幅值
图7 所示在不同的深度参数下,宽度匹配后的FFT最大幅值,从图中可以看出即使是在不同的深度下也会存一个最小的幅度值。
基于以上分析无论是深度或宽度都存在一个最小的幅值。如果取一个比较小的深度值,虽然可以抑制机械谐振;但长期运行将会降低机械设备的使用寿命。因此为了能更好地对机械谐振进行抑制,可通过优化方法来匹配最优陷波滤波器参数。
4.2 优化方法
在理想的情况下,深度参数和幅值呈现单峰曲线,但是当在噪声和负载变化时并不是单峰曲线,为了避免使参数陷入局部最优,本文采用改进粒子群优化算法(PSO)对参数进行优化。
粒子群优化(PSO)是J.Kennedy和R.Eberhart提出的基于群体智能的计算技术,是迭代的优化工具。粒子群优化算法(PSO)参数设置较少,算法简单,因此被广泛应用。为了能快速收敛和取消最大速度的限制,文献[10]中的压缩因子γ来代替惯性权值,其改进更新过程如下
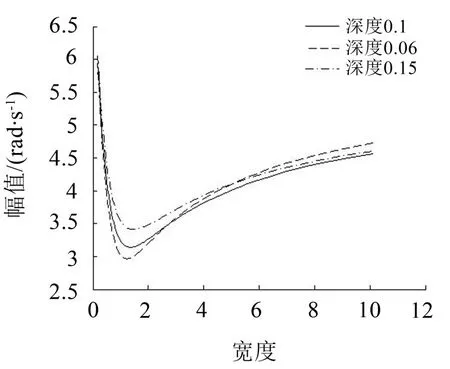
图7 不同宽度幅值

为了简化计算,将式(8)和式(10)的深度参数和宽度参数进行优化。其参数优化步骤如下:
步骤1:设置种群规模M和迭代次数N,随机初始化各个粒子的位置x和速度v,且每个粒子都包含两个变量。
步骤2:匹配滤波参数后,采集速度偏差,计算FFT变换后谐振频率处的幅值作为适应度。
步骤3:比较每个粒子的当前适应度和自身的最优值Pbest。若当前的适应度优于Pbest,则当前适应度更新为Pbest,并设定Pbest的位置为当前位置。
步骤4:比较每个粒子当前的适应度与种群的最优解gbest,如果当前适应度优于gbest,则将gbest设置为当前粒子的适应度。
步骤5:采用式(15)和式(17)更新群体中的各个粒子的位置和速度。
步骤6:判断是否满足终止条件,即达到最大迭代次数或小于给定的误差精度,如果满足条件则输出深度参数和宽度参数,否则转步骤2继续迭代。
步骤7:得到最优的宽度和深度参数。
5 实验仿真
5.1 仿真结果
仿真参数如表1所示,速度的给定值为3000 rad/s。仿真过程中为了能使FFT变换后的频率分辨率高并且运算量小,采样点数为1024点,采样频率为1 kHz。

表1 仿真参数

图8 优化后速度响应
图8 是获得优化参数后的速度响应曲线。图9是在获取幅频特性图之后,手动设置陷波滤波器的深度参数为0.16时的速度响应曲线。从两幅图的速度响应曲线可以看出优化后的速度响应曲线逐渐变得平滑,而手动设置参数的速度响应曲线有小幅度振荡。
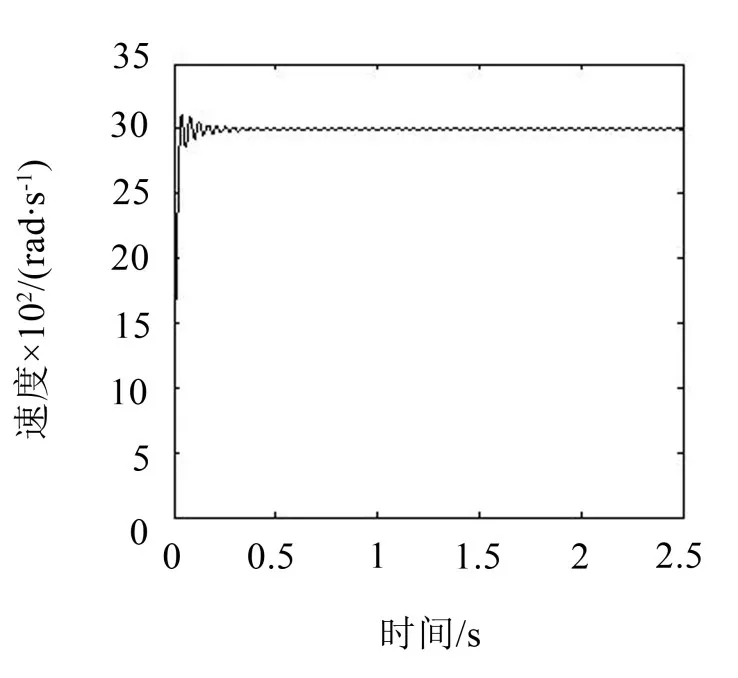
图9 设定参数速度响应曲线
图10 是优化后的幅频特性和未优化的幅频特性图。从图中可以看出优化可以抑制69%的谐振幅值,大大降低机械谐振。
图11是迭代次数和深度参数的变化图,从图中可以看出迭代10次以后深度参数收敛于0.0897,收敛速度快。
5.2 实验结果
谐振实验平台如图12所示。工控机连接转接板,转接板连接测试平台400 W的电机,电机连接谐振平台的同步带。在谐振测试平台上可以通过安装负载的方法来改变谐振频率。
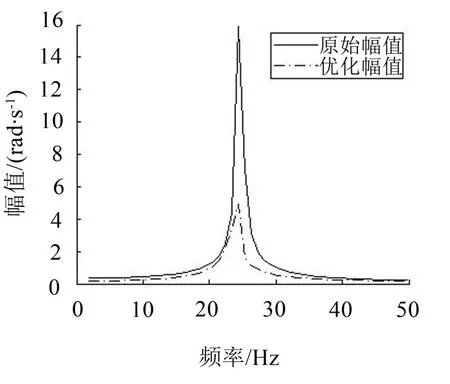
图10 优化前后幅频特性对比图
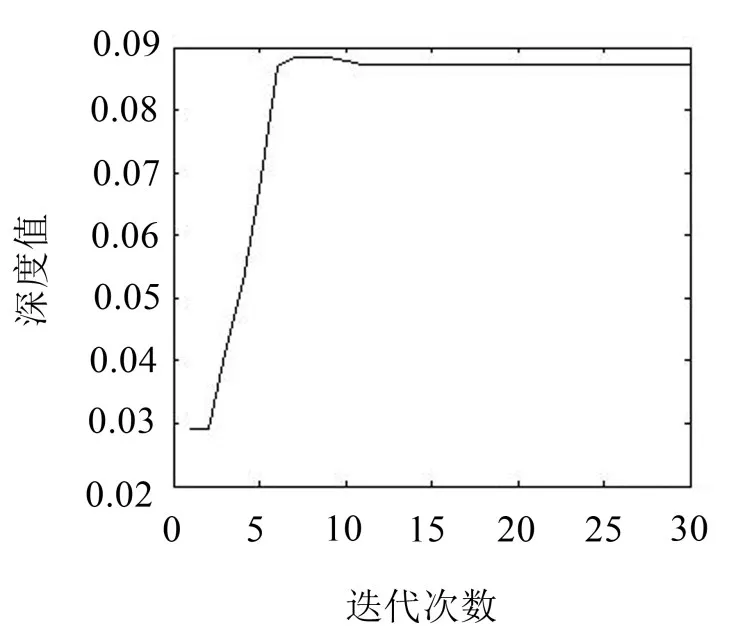
图11 迭代次数和深度变化图
用Labview编写的伺服系统速度环的运算周期是0.125 ms,即采样频率为8 kHz。实验中采样点数越多,FFT变换后频率的分辨率越高,但是数据存储量大且运算时间长,综合考虑最终选择点数为4096。
图13是在速度给定为150 r/min时的幅频特性图,经过分析得出谐振频率为251 Hz。在经过优化陷波谐振抑制之后的FFT如图14所示。
通过图中的曲线可以看出参数优化可以大幅度降低机械谐振。
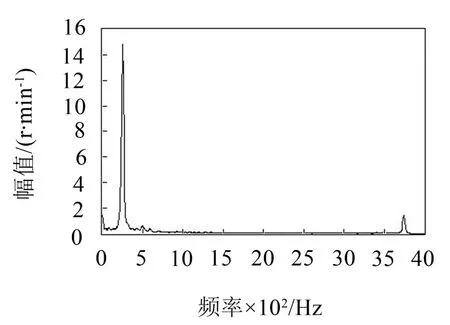
图13 初始FFT变换图

图14 优化抑制后的FFT
6 结语
(1)本文针对离线条件下陷波滤波器不能设置合适的参数而使谐振抑制效果不理想的问题,在分析了陷波滤波参数对谐振影响的基础上,提出了一种机械谐振抑制参数优化方法。
(2)分析了不同弹性系数的谐振系统中,对配置的陷波滤波参数得到FFT的谐振幅值会存在一个最优值。然后利用改进型粒子群算法寻找最优的深度和宽度值。实验结果表明改进型粒子群优化算法(PSO)可以快速收敛。
(3)对离线陷波参数的速度响应曲线和参数优化后的速度响应曲线进行比较,结果表明优化后的速度响应曲线更加平滑;从仿真和实物实验看出最大谐振抑制幅度可以降低原来最高幅值的69%,大大提高了谐振抑制能力,同时优化提高了谐振抑制的效率。
[1]杨明,王璨,徐殿国.基于轴矩限幅控制的机械谐振抑制技术[J].电机与控制学报,2015,19(4):58-64.
[2]WANG W,XU J,SHEN A.Detection and reduction of middle frequency resonance forindustrialservo[C].International Conference on Information Science and Technology.IEEE,2012:153-160.
[3]王璨,杨明,徐殿国.基于PI控制的双惯量弹性系统机械谐振的抑制[J].电气传动,2015,45(1):49-53.
[4]杨明,郝亮,徐殿国.基于自适应陷波滤波器的在线机械谐振抑制[J].哈尔滨工业大学学报,2014,46(4):63-69.
[5]李娜,李世华.基于自适应IIR滤波器的伺服系统机械谐振抑制[C].第27届中国控制与决策会议,2015:3418-3423.
[6]李宗亚,罗欣,沈安文.基于陷波器参数自调整的伺服系统谐振抑制[J].计算技术与自动化,2013,32(4):7-11.
[7]KIM T I,BAHN W,YOON J M,et al.Online tuning method for notch filter depth in industrial servo systems[C].Chinese Control Conference,2016:9514-9518.
[8]LEE D H,LEE J H,AHN J W.Mechanical vibration reduction control of two-mass permanent magnet synchronous motor using adaptive notch filter with fast Fourier transform analysis[J]. Iet Electric Power Applications,2012,6(7):455-461.
[9]KANG J,CHEN S,DIX.Onlinedetectionand suppression of mechanical resonance for servo system[C].Third International Conference on Intelligent Control and Information Processing.IEEE,2012:16-21.
[10]王秋生,杨浩,袁海文.基于粒子群优化的数字多频陷波滤波器设计[J].仪器仪表学报,2012,33(7):1661-1667.

