PE80聚乙烯管道焊接接头的应力松弛模型验证及安全评价
陈锦裕,王 佳,曾 多
(福建福清核电有限公司,福建 福清 350318)
0 前言
PE是一种常见的聚合物工程材料,由于具有显著的长期耐环境腐蚀性、安装与维护成本低、力学性能好等优点,而被广泛用于水和天然气的运输网络[1]。统计数据表明,在新安装的天然气管道系统中,超过90 %的管道是PE管道[2]。
据调查,1982年美国Duke Energy公司Catawba核电站中应用高密度聚乙烯(PE-HD)管对其2#机组发电氢冷器的DN150核DN200供回水A106碳钢管采用SDR11的PE-HD管进行替换,该系统运行至今未发现任何腐蚀、结垢。尽管PE管道被广泛应用,但是PE材料的安全性同样不可忽视。近些年来PE管道失效引发的灾难性事故时有发生,特别是在水和天然气管道运输系统中由于PE材料的长期脆性失效及快速与缓慢裂纹扩展。目前在市场上广泛应用的主要有PE-HD管道、中密度聚乙烯(PE-MD) 管道和低密度聚乙烯(PE-LD)管道,根据PE管道50年内能承受的最小压力为100 kg或80 kg标记为PE100或PE80。大量工程实践证明[3-6],管道系统出现的失效问题多数在连接处,管道焊接品质的好坏对管道系统的安全及使用寿命有直接的影响,因此急需研制出能够用于含缺陷PE管道的安全评价系统。
据统计,目前PE-MD80在天然气管道输送中使用最广泛,故本文主要以PE-MD80为研究对象,对含缺陷PE-MD80管道进行安全评价。
1 核级PE管道焊接接头力学性能分析
PE管道能否长期安全稳定的服务于天然气等管道系统[7],主要取决于管道焊接接头的品质。为了研究方便,实验样品采用热熔焊接接头进行试验。
1.1 焊接实验样品制备
焊接材料选用某企业生产的PE-MD管材,采用意大利CNC ASIA 250 FA 型全自动热熔对接焊机进行焊接,先将PE-MD管材或管件的横截面端面用铣削机处理平整,再用具有特定压力的加热板使连接部位加热至熔融状态,立即移走加热板,施加一定压力将2个熔融端面压在一起,最后在稳定的压力作用下将2个部件连接并固定,直至接头冷却。据现行PE管道热熔焊接 DVS 2207-1标准,各参数的选取范围见表1。

表1 DVS 2207-1标准中各参数的取值范围Tab.1 Parameter scale of DVS 2207-1
取样后将试样进行二次加工,制备成在热熔接头两侧带卷边和去除卷边2类试样。试样制备完毕后需要将试样置于(25±2) ℃的环境中进行状态调节6 h±30 min,以消除机加工时在材料内部形成的残余应力和温度差异对力学试验的影响。试样加工成型的实物如图1所示。

(a)热熔焊接试样 (b)热熔接头实验试样图1 热熔焊接接头试样Fig.1 The specimens of hot melt welded joint specimens
1.2 松弛试验
为了研究PE焊接接头的松弛与蠕变性能,得出PE焊接接头的本构方程。对PE焊接接头试样进行松弛试验。试验设备与试验环境如文献[8]所述,采用微机控制电子万能试验机(CMT-4104),试验试样在(28±2) ℃的环境下静置6 h以上;把试样分成3组进行试验,3组的斜坡加载时间分别为7、1 800 s和7 200 s,试验数据处理结果如图2所示。为了进一步研究PE焊接接头与PE母材松弛效应的差异,将试验所得的松弛曲线进行对比。

1—瞬时加载,t0=7 s(焊接接头) 2—斜坡加载,t0=1 800 s(焊接接头) 3—斜坡加载,t0=7 200 s(焊接接头) 4—瞬时加载,t0=7 s(母材) 5—斜坡加载,t0=1 800 s(母材) 6—斜坡加载,t0=7 200 s(母材)图2 PE母材与焊接接头的松弛试验曲线Fig.2 Relaxation test curve of polyethylene base metal and welded joint at different loading time
从图2可以看出,随着斜坡加载时间的增加,实验得到的应力最大值逐渐减小。这是由于在加载过程中,应力松弛已经发生。PE焊接接头在松弛开始阶段应力迅速衰减。随着时间的推移,松弛应力变化率逐渐减小。不管斜坡加载时间多大,最终都趋于恒定值。可见PE焊接接头同样具有松弛效应,变化趋势与PE母材一致。
对比PE焊接接头与PE母材的松弛曲线得出,在初始应力σ0不同的前提下,PE母材与焊接接头的松弛趋势基本一致,也就是瞬时应力与初始应力比值非常相似。因此对于PE焊接接头的本构方程可以用只改变材料的瞬时弹性模量而不改变Prony级数来表示。
2 PE管道焊接接头的本构模型
研究表明[8],当PE材料的应力低于屈服应力值的60 %或者应变小于0.01时,可以用线黏弹性理论来研究PE材料。PE管道在温度变化约55 ℃才会引起0.01的应变。在工程实际中温度变化很少能达到55 ℃,松弛试验中的应变也没有超过0.01,所以本文近似采用线黏弹性本构模型,用Prony级数表示松弛函数的Maxwell黏弹模型,对PE材料进行分析计算。
对于松弛试验,在恒定应变下的本构关系可表示为式(1):
σ(t)=Y(t)·ε0
(1)
式中σ(t)——应力方程
Y(t)——松弛方程
i0——应变
松弛方程采用Prony级数的典型模型如式(2)所示:
(2)
式中pi——第i个Prony常数(i=1,2,…)
τi——第i个Prony松弛时间常数(i=1,2,…)
E0——材料的瞬时弹性模量,MPa
M——Prony级数的阶数
用非线性曲线拟合,综合优化分析计算软件平台1stOpt对试验数据进行拟合,得出的PE管道焊接接头用Prony级数表示的本构模型参数如表2所示。通过拉伸实验计算出PE焊接接头的瞬时弹性模型量为345.1 MPa,文献[8]实验得出的PE管道用Prony级数表示的本构模型参数。PE焊接接头的本构方程可以用只改变材料的瞬时弹性模量(E0)而不改变Prony级数来表示。我们直接得出PE焊接接头的本构模型。

表2 实验用PE-MD焊接接头Maxwell本构模型参数Tab.2 Laboratory PE-MD weld ’s Maxwell constitutive model parameters
为了验证2组材料参数的准确性,分别用2种材料在Abaqus软件中进行有限元仿真分析,模拟PE材料的松弛行为,得出的2组应力比值随时间的变化规律如图3所示。

1—有限元模拟(拟合法) 2—有限元模拟(直接法) 3—误差百分比图3 PE焊接接头的松弛应力曲线Fig.3 Stress relaxation curve of polyethylene weld
从图3可以看出,通过有限元分析软件得出的应力松弛曲线基本一致,相对误差基本保持在2 %以内,只有在斜坡加载的最大应力值附近的误差达到4 %左右。所以可以得出通过拟合法或者直接法得到的PE焊接接头本构模型具有同等效果。
3 核用PE管道缺陷的安全评价
PE管道在安装或者焊接过程中,难免会产生缺陷。这些缺陷往往成为PE燃气管道发生失效的重要原因。研究表明,大多数的PE管道失效来源于准脆性断裂行为,也就是PE管道的缓慢裂纹增长。裂纹缺陷的危险性是肯定的,但是工程实际中并不能满足100 %无缺陷施工。这就有必要对PE缺陷进行安全评价。关于电熔接头各类型缺陷的安全评定文献[9]已有研究,本文主要对热熔焊接管道裂纹缺陷进行评价。
3.1 缺陷表征及断裂判据
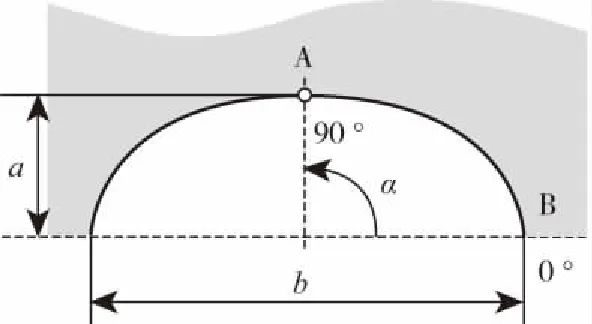
图4 裂纹缺陷的平面模型Fig.4 Plane model of crack defects
裂纹缺陷一般为椭圆形,a为裂纹深度,b为裂纹长度,如图4所示。Barker[10]研究表明对于小裂纹缺陷的b/2a值应该趋近于1.1。所以在裂纹尺寸较小时接近半圆形[11],随着裂纹长度的增加,b/2a值也随之增加,并且a和b的值遵守式(3)的经验公式。
(3)
式中s——管道的厚度,mm
a——裂纹深度,mm
b——裂纹长度,mm
大多数PE管道失效都属于准脆性断裂行为,也叫做缓慢裂纹增长(SCG)。在这种情况下,塑性变形只发生在裂纹尖端附近,满足小范围屈服条件。所以可以用线弹性断裂力学(LEFM)来描述裂纹尖端应力场[12-13]。在LEFM中描述裂纹尖端附近的应力分布是通过应力强度因子K来描述的。应力强度因子是外部载荷、结构的几何形状和焊缝的物理形状。对于I类裂纹的K可以用式(4)表示:
(4)
式中a——裂纹的长度,mm
Y——裂纹形状因子,mm
裂纹扩展速率可以用式(5)的幂律关系来表示:
(5)
式中A——PE材料的参数
m——PE材料的参数
目前对于PE含缺陷管道的评价体系还不够完善,本文借鉴GB/T 19624—2004及ASME采用式(6)的断裂判据对PE管道进行安全评价。
KI≤KIC
(6)
式中KI——I型裂纹应力强度因子,MPa·mm1/2
KIC——临界应力强度因子,MPa·mm1/2
3.2 PE管道KIC值的确定
Graice、Younan和Naga[14]参照ASTM公布的测试材料临界断裂韧度(JIC)方法,对PE100和PE80管道的JIC进行测试。采用紧凑拉伸试件(CT Specimens)和单缺口弯曲试件(SENB Specimens)进行测试的结果如表3所示。

表3 PE管道的JIC值Tab.3 JIC values of polyethylene pipes
从表3可以发现,PE管道的JIC值并不是随着管道的厚度增大而增加。为了保证管道的安全性。加上本文所研究的PE管道为PE80管道。所以取PE管道的JIC值为0.33 kJ/m2。利用式(7)求得PE管道的KIC值为12.10 MPa·mm1/2。
(7)
式中J——断裂韧度,kJ/m2
E——弹性模量,MPa
μ——泊松比
3.3 含缺陷PE管道KI值有限元计算
为了评定内压下含裂纹缺陷PE管道的剩余寿命,有必要计算出裂纹扩展KI的变化情况。因此建立含裂纹缺陷PE管道的有限元模型,利用Abaqus分析软件进行计算。
3.3.1 模型建立
含裂纹缺陷的PE管道模型如图5所示,PE管道的尺寸采用标准尺寸比,标准尺寸比是管道外径d与管道名义厚度s的比值。工程实际中常用的标准尺寸比有6、7.4、9、11、13.6、17和26。所以选用如表4所示的管道类型,每组分别建立15个裂纹模型,总共105个模型进行有限元分析计算。

图5 含裂纹缺陷的PE管道模型Fig.5 Polyethylene pipe model diagram containing crack defects
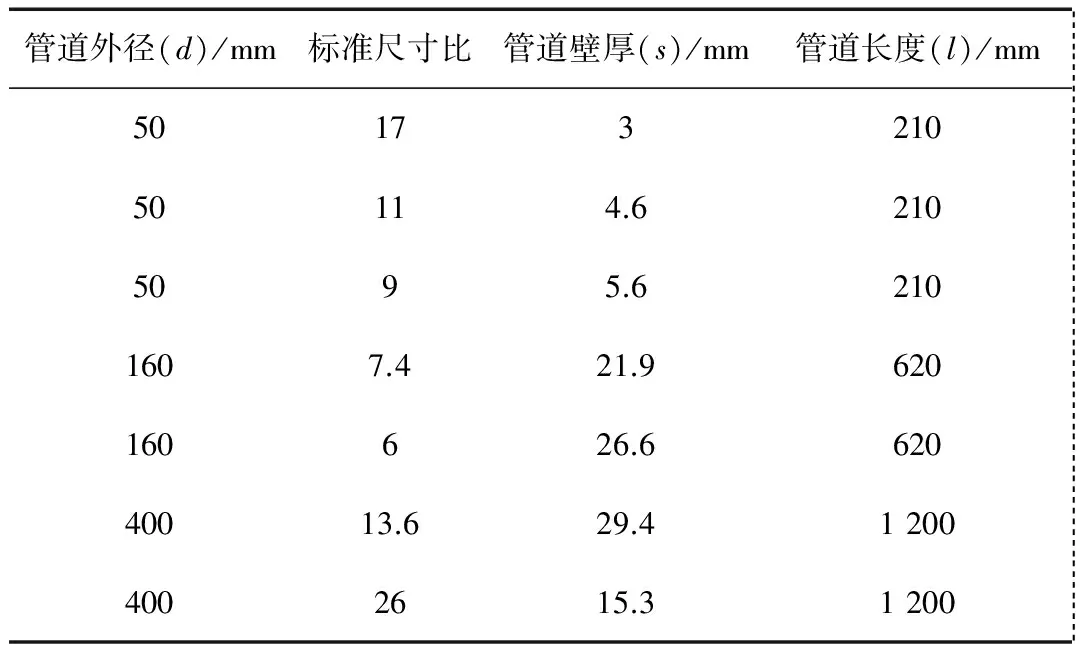
表4 管道模型的几何尺寸Tab.4 Pipe geometry size of the model
在分析过程中为了更真实的模拟PE焊接管道的实际性能,将焊缝部分与母材部分分开建模,分别赋予了不同参数的本构模型进行分析,具体如图6所示。由于计算KI的特殊性,特采用软件对裂纹尖端的网格进行特殊处理来满足裂纹尖端的奇异性。具体的网格划分情况和裂纹尖端网格情况如图7所示。

图6 PE管道有限元模型不同材料参数设置示意图Fig.6 Polyethylene pipe schematic finite element model of different material parameters settings

图7 PE管道裂纹尖端网格划分详图Fig.7 Detail of polyethylene pipe crack tip meshing
3.3.2 材料参数的确定
本次分析模型中包含PE母材和PE焊缝2种材料,关于他们的材料特性及参数详见表2。关于式(5)中提及的材料参数A和m参考,Stern[15]的研究成果分别取2.42×10-4和2.17。
3.3.3 有限元分析结果
含裂纹缺陷PE管道受到内压作用下的应力场有限元分析结果如图8所示。从图8的应力云图可以发现,Mises应力的最大值主要分布在裂纹顶端及底部的两端。

图8 PE裂纹缺陷在内压下的应力云图Fig.8 Polyethylene crack defects under internal pressure stress nephogram
为了研究裂纹深度对裂纹尖端应力场的影响,分别选取了不同裂纹深度系数(裂纹深度与材料厚度之比a/s)进行建模和分析,得出K与Y随着a/s的变化情况如图9所示。从图9可以得出,K和Y随着a/s的增大而增大。变化情况可以分为3个阶段,第一阶段(0~0.15)迅速增大;第二阶段(0.15~0.45)开始缓和;第三阶段(0.45~1)快速爬升。

▼—K ▲—Y图9 K、Y随着a/s的变化情况Fig.9 K and Y changes along with a/s
使用Sigmaplot软件对Y与a/s的变化关系进行拟合。其中一组数据拟合后的结果如式(8)所示:
(8)

—判定曲线方法,标准尺寸比:▲—有限元法,17 —拟合法,17 ▼—有限元法,11 —拟合法,11 ◆—有限元法,9 ·· —拟合法,9 ●—有限元法,6 ····—拟合法,6 ★—有限元法,7.4 ………—拟合法,7.4图10 中小管径管道K的有限元值与拟合值对比Fig.10 Small diameter pipeline stress intensity factor of the finite element value and fitting value contrast figure
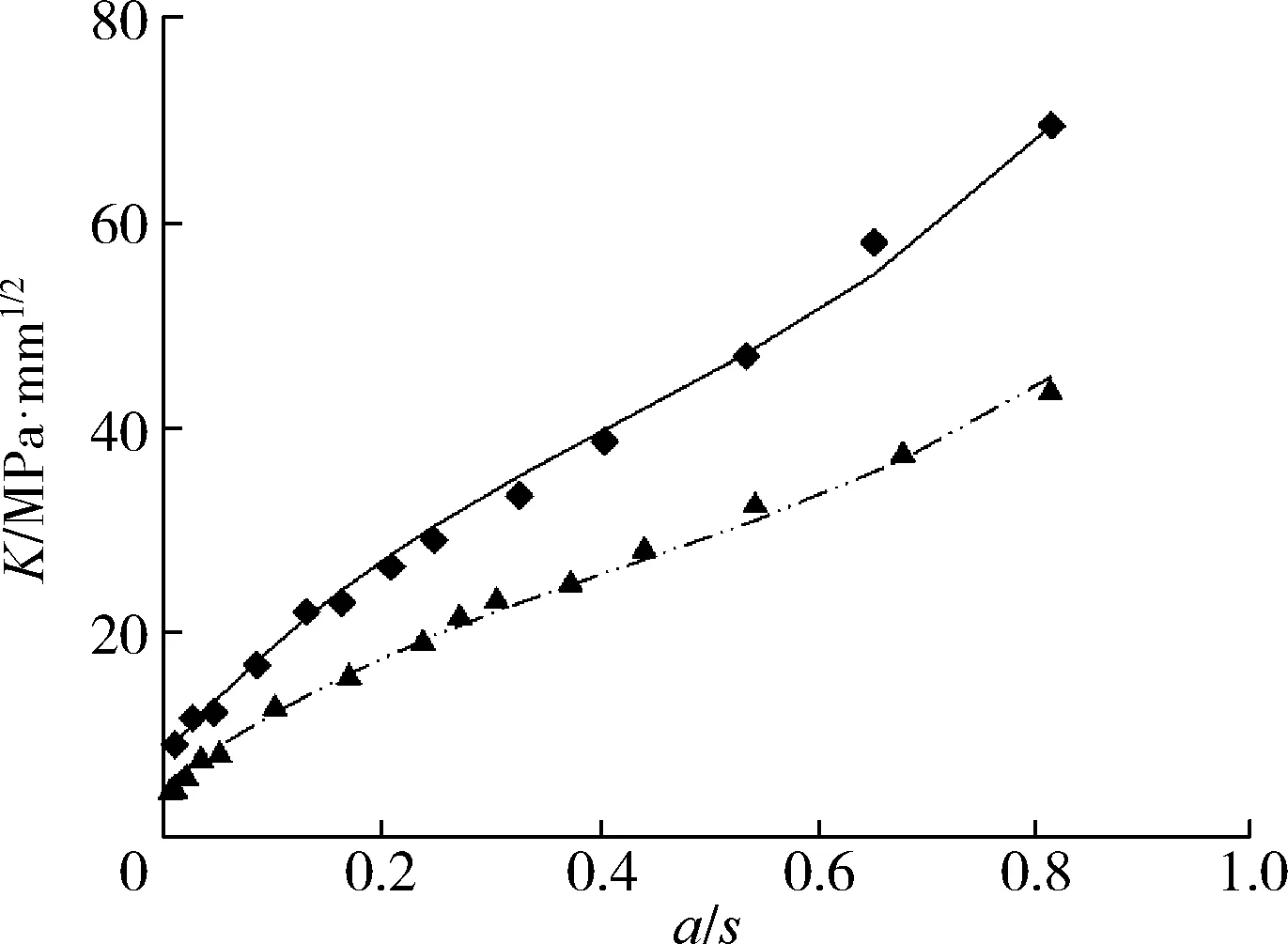
方法,标准尺寸比:◆—有限元法,26 —拟合法,28 ▲—有限元法,13.6 ····—拟合法,13.6图11 大管径管道K的有限元值与拟合值对比Fig.11 Big diameter pipe stress intensity factor of the finite element value and fitting value contrast figure
为了验证式(8)的可靠性,把另外6组数据作为验证。验证结果如图10、图11所示。有限元值与式(8)所得的值误差不到5 %。可见式(8)具有较高的准确度。同时从图10可以看出,对于直径相同的PE管道,在内压不变的情况下,随着标准尺寸比的增加,K也随着增加。所以对于受到内压的PE管道的KI可以用式(9)表示:
(9)
式中P——压力,MPa
3.4 含裂纹缺陷PE管道安全评价

—判定曲线方法,标准尺寸比:▲—有限元法,17 —拟合法,17▼—有限元法,11 —拟合法,11 ◆—有限元法,9 ·· —拟合法,9 ●—有限元法,6 ····—拟合法,6 ★—有限元法,7.4 ………—拟合法,7.4图12 PE焊接接头裂纹缺陷失效判定图Fig.12 Polyethylene welded joint crack defects failure determination
利用式(4)的断裂判据及PE管道的KIC的试验值,就能对含裂纹缺陷的PE管道进行安全评价。已知KIC的取值为12.10 MPa·mm1/2。可以得出所计算模型的失效评价如图12所示。从图12可知,处于判定曲线下方的含缺陷裂纹管道模型是安全的,处于判定曲线上方的含裂纹缺陷管道模型是不安全的。
结合图12的失效判定图,在已知裂纹缺陷的几何参数的情况下,根据Y与a/s的表达式求出模型的几何因子,并代入式(9)求出缺陷的KI,判断点(a/s,K)处于图中的哪个区域,就能对PE缺陷模型进行安全评价。
4 结论
(1)含裂纹缺陷的PE管道的最大Mises应力主要分布在裂纹的顶端及底部两端;最大Mises应力并不简单的随着a/s的增大而增大,而是呈现波动状态;在裂纹尖端附近的应力场分布情况基本不随a/s的变化而变化;
(2)对于同种尺寸的PE管道,应力强度因子(K)和裂纹形状因子(Y)随着a/s的增大而增大,变化情况可以分为3个阶段,第一阶段迅速增大;第二阶段趋于缓和;第三阶段快速爬升;在管道直径和a/s相同的情况下,K值随着标准尺寸比的增大而增大;
(3)影响PE缺陷管道K的最大因素是Y;PE缺陷管道的Y可以拟合成与a/s相关的多项式,经过有限元分析验证得出该表达式具有很高的精度;
(4)根据拟合后的裂纹Y的表达式结合缺陷管道所受的载荷就能直接得出PE管道裂纹缺陷的K;最后利用PE管道裂纹缺陷的失效判定图就能直接对管道进行安全评价。
参考文献:
[1] KIASS N, KHELIF R, BOULANOUAR L, et al. Experimental Approach to Mechanical Property Variability Through a High-density Polyethylene Gas Pipe Wall[J]. J Appl Polym Sci, 2005, 97(1): 272-281.
[2] KRISHNASWAMY R K. Analysis of Ductile and Brittle Failures from Creep Rupture Testing of High-density Poly-ethylene (HDPE) Pipes[J]. Polymer, 2005, 46(25): 11 664-11 672.
[3] SHALABY H, RIAD W, ALHAZZA A, et al. Failure Analysis of Fuel Supply Pipeline[J]. Eng Fail Anal, 2006, 13(5): 789-796.
[4] AZEVEDO C R. Failure Analysis of a Crude Oil Pipeline[J]. Eng Fail Anal, 2007, 14(6): 978-994.
[5] MAJID Z, MOHSIN R, YAACOB Z, et al. Failure Ana-lysis of Natural Gas Pipes[J]. Eng Fail Anal, 2010, 17(4): 818-837.
[6] ADIB A, DOMINGUEZ C, RODRIGUEZ J, et al. The Effect of Microstructure on the Slow Crack Growth Resistance in Polyethylene Resins[J]. Polymer Engineering & Science, 2015, 55(5): 1 018-1 023.
[7] 朱志彬, 陈丽静, 杨晓翔, 等. 含球孔缺陷聚乙烯管道热熔接头力学性能分析[J]. 石油化工设备, 2014, 43(3): 30-33.
ZHU Z B,CHEN L J,YANG X X, et al. Mechanical Properties Analysis of Polyethylene Pipe Hot Melt Connectors with Ball Hole Crack[J]. Petro-Chemical Equipment, 2014, 43(3): 30-33.
[8] 陈锦裕,朱志彬,杨晓翔. PE80燃气管道的应力松弛模型与实验验证[J]. 中国塑料, 2016, 30(4): 93-98.
CHEN J Y,ZHU Z B,YANG X X.Viscoelasticity Mechanics Model of Medium Density Polyethylene Pipes[J].China Plastics, 2016, 30(4): 93-98.
[9] 施建峰, 郭伟灿, 师 俊, 等. 聚乙烯及其复合管道安全检测与评价方法[J]. 化工学报, 2013, 64(2): 756-764.
SHI J F,GUO W C,SHI J, et al. Development of Non-destructive Testing and Safety Assessment of Polyethylene and Composite Pipes[J].CIESC Jorunal,2013, 64(2): 756-764.
[10] BARKER M, BOWMAN J, BEVIS M. The Perfor-mance and Causes of Failure of Polyethylene Pipes Subjected to Constant and Fluctuating Internal Pressure Loadings[J]. J Mater Sci, 1983, 18(4): 1 095-1 118.
[12] ANDENA L, RINK M, FRASSINE R, et al. A Fracture Mechanics Approach for the Prediction of the Failure Time of Polybutene Pipes[J]. Eng Fract Mech, 2009, 76(18): 2 666-2 677.
[13] FRANK A, PINTER G, LANG R W. Prediction of the Remaining Lifetime of Polyethylene Pipes After up to 30 Years in Use[J]. Polym Test, 2009, 28(7): 737-745.
[14] GRAICE I M, YOUNAN M Y, NAGA S A R. Experimental Investigation into the Fracture Toughness of Polyethylene Pipe Material[J]. J Press Vess-T Asme, 2004, 127(1): 70-75.
[15] STERN A. Fracture Mechanical Characterization of the Long-term Behavior of Polymers Under Static Loads: [D]. Austria: University of Leoben,1995.

