巧解一个连接体问题
文 长沙市南雅中学K1601 李晟阳
连接体问题是力学中学生能力考查的重要内容。在学习斜面-滑块组成的连接体问题时,我发现了一个有趣的结论,下面通过具体问题进行阐述。
一、问题的提出
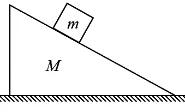
图1
问题1.如图1所示,木楔M置于粗糙的水平地面上,一物块以某一初速度沿斜面滑下时,物块恰好保持匀速直线运动,整个过程中木楔始终保持静止状态。分析地面对木楔是否存在摩擦力。
滑块除了受重力外,还受到斜面对滑块的支持力和滑动摩擦力。滑块在斜面上做匀速直线运动,斜面对滑块的作用力与滑块重力等大、反向,即斜面对滑块的作用力(支持力和滑动摩擦力的合力)方向竖直向上,如图2所示。根据牛顿第三定律可知,物块对木楔的作用力始终竖直向下,地面对木楔没有摩擦力。
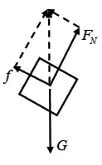
图2
上述分析过程运用了隔离法,依次以滑块和木楔作为研究对象进行受力分析。由滑块做匀速直线运动及木楔保持静止可知两者的加速度相同且为零,两者视为一个整体,该整体所受的外力分别为竖直向下的重力和竖直向上的地面支持力,可得出地面对木楔没有摩擦力。
问题2.在问题1的基础上,若施加一个竖直平面内的作用力 在物块上,如图3所示,地面对木楔否存在摩擦力?

图3
解决该问题通常的做法是分别对滑块和木楔受力分析,再结合牛顿运动定律列出方程求解。但这种处理方法计算复杂,有没有更简洁的方法?
我认为可分析两种特殊的受力情形。
二、两种特殊受力情形
问题3.在问题1的基础上,若作用在滑块上的力竖直向下,如图4所示,地面对木楔是否存在摩擦力?
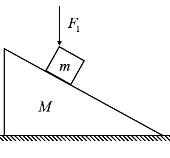
图4
这个问题的可从以下两个方面考虑。
1.对滑块受力分析,与问题1的分析类似,滑块受力如图5所示,建立直角坐标系,由牛顿第二定律列出方程组
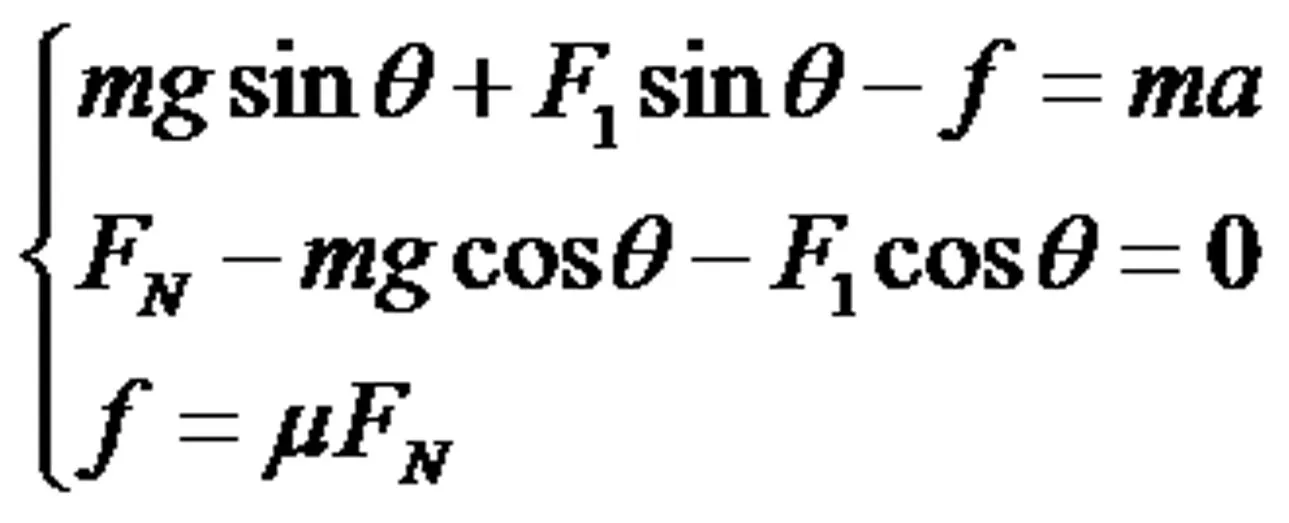
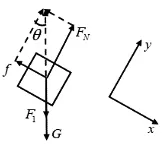
图5
其中 为物块的质量, 为物块与斜面间的动摩擦因数,
为斜面与水平面的夹角,1为施加在滑块上的外力。根据已知条件及问题1得出 =tan ,代入上述方程组得滑块的加速度为零,即滑块仍然做匀速直线运动,再运用整体法得知地面与木楔之间没有摩擦力。
2.设想在滑块顶角上放置另一物体,根据问题1,其与滑块构成的一个整体仍将做匀速直线运动,若此时该物体对滑块的作用力恰好也为1,则滑块的受力与问题3中情形完全相同,因此两者的运动情况也相同,再由整体法同样可以得出以上结论。
问题4.在问题1的基础上,若作用在滑块上力沿斜面向下,如图6所示,地面对木楔又是否存在摩擦力?
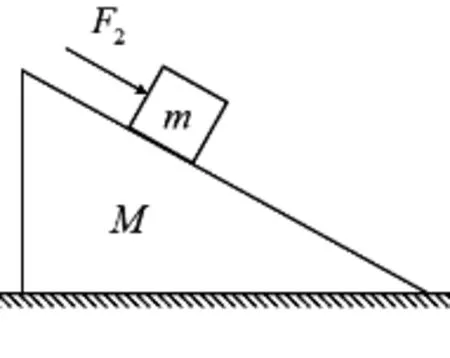
图6
滑块所受外力2并没有改变滑块与斜面间的正压力,因此两者之间的摩擦力不变。若以木楔为研究对象,木楔此时的受力与问题1中的情况完全一样,木楔与地面之间同样没有摩擦力。
三、问题的解决
在回答问题2之前,需要了解一下高中数学中有关平面向量(矢量)的知识。在平面内任意一个向量 都可以由两个不共线的单位向量线性表示,即其中α,β为常数。
在力学中,力也是向量且满足向量的基本性质,为使问题简化,不妨设想问题3和问题4中的两个外力为竖直平面内的一对单位力(向量),则任意竖直平面内的作用力都可表示为
理解为将外力两个特殊的方向分解,分离大小分别为 , 。
对问题3、问题4的分析可知存在时,地面对木楔没有摩擦力的作用,于是问题2中在外力作用下,木楔与地面之间仍没有摩擦力。
由此可以在问题1的基础上得出这样一个结论:当物块与斜面之间的动摩擦因数满足 =tan( 为斜面倾角)时,只要滑块沿斜面向下滑动,则无论作用在滑块上的外力的大小和方向如何变化,木楔与地面之间始终没有摩擦力。
本文通过对斜面-滑块模型的研究得出的结论是从滑块的两种特殊受力情形出发,结合高中数学中的平面向量知识后总结分析出来的。该结论在解决相关的动力学问题时能有效减少物体的受力分析,降低该问题的复杂程度。

