考虑井壁摩擦随机性的钻柱动力学模型

田家林， 杨应林， 杨 琳, 吴志鑫， 申 彤， 李 蕾(.西南石油大学 机电工程学院，成都 60500；2.西南交通大学 机械工程学院，成都 6003)

随着传统油气资源日趋枯竭，新型油气资源开采力度逐渐增大，如页岩气、煤层气等，使钻井工程面临更为复杂的地层工作环境。在现有钻井技术基础上，大位移定向井、水平井、分支井技术迅速发展与应用。以页岩气开采中的大位移水平井为例，随着靶径的增加，井壁摩擦作用对钻柱动力学特性的影响所占比重越来越大，运用现有研究方法与结论已不能满足实际需求[1-3]。因此进行井壁摩擦随机性分析及其对钻柱动力学特性影响研究，对于发展新型油气资源开采能力，提高复杂井身钻井水平，具有重要的实际意义。

钻井过程中，井下工况非常复杂，钻头破岩导致钻柱振动，而过于强烈的振动容易导致液压及电控系统出现过载或损坏等现象，给安全生产带来一定隐患[4]。随着各种新工艺不断应用，钻进时井壁摩擦影响因素众多，使井下工具安全评价、提速增效研究面临新挑战。越来越多的学者与研究机构也认识到此问题的重要性，但是研究结论与实际情况仍然存在较大差异，对于井壁摩擦行为的描述方法有待进一步完善[5-7]。实际上，忽略钻柱与井壁摩擦的随机性，或者不能准确描述摩擦因数随机场，都不能真实深入地反映钻柱动力学特性[8]。

基于此，本文在前期研究的基础上，结合井下实际工况，进行井壁摩擦随机性以及其对钻柱动力学的影响研究。首先进行井壁摩擦行为的分析，给出建立井壁摩擦随机场的步骤，得到井壁摩擦随机行为的描述方法。然后结合页岩气开采的工程背景，进行水平井钻柱动力学模型分析，建立动力学模型，给出各力的求解方法。考虑钻杆各点的接触情况，给出动力学模型的离散方法。为验证理论模型的准确性，进行试验测试和算例分析，根据实验测试确定基本输入参数，将得到的振动速度，与试验测试、定摩擦方法得到的结果以及关键参数进行对比分析。

文章研究成果可为新型油气资源开采条件下的钻柱动力学研究提供参考，同时，由于钻柱动力学结果是进行井下工具动载荷失效、岩石破碎效率评价的前提与依据，所以，研究成果也可为井下安全生产、提速增效方法与工具研究提供理论依据，对指导现场生产具有实际意义。

1 井壁摩擦随机性研究

结合水平井工况条件，首先进行钻柱受力分析并建立分析模型,如图1所示。其中，左边界为分析段的坐标原点，Fsta为分析段左边界等效作用力，Ffric为井壁对钻柱的摩擦力，G为分析段钻柱重力，m为分析段质量，g为重力加速度，Fhar为钻井液对钻柱的作用力，Fbit为岩石对钻头的作用力，且Fbit的大小与钻压WOB(weight on bit)相等。

图1 钻柱受力分析Fig.1 The forces analysis of drill string

井壁对钻柱的摩擦力的重要特点在于其随机性，体现在接触副的产生位置、摩擦因数大小发生随机改变。数学方法描述的准确性对于计算结果的精度具有决定作用。考虑井壁对钻柱摩擦作用的特点，为了研究摩擦副产生位置的随机性，引入与位移x对应的随机变量ξ。对于摩擦因数，通过统计分析井壁对钻柱摩擦作用的随机数据，随机数据呈现出的分布规律可用高斯分布近似描述，建立相应的分析方法。建立井壁对钻柱随机摩擦力分析模型为

(1)

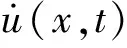
f(x,ξ)的概率密度计算公式为

(2)

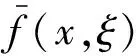
(3)

式中:{λi}与{φi(x)}分别为特征值与特征函数;Zi(ξ)为互不相关的随机变量。式(3)展开的优势在于在高斯平稳场中一定是收敛的，相对于其他类型展开，在展开相同有限项时具有最小的均方误差。根据钻井过程井下工况，定义x为空间点坐标，则有x=(x1,y1)，可进行二维随机场研究。同理，基于二维随机场的构建方法，可得到一维随机结果。

Zi(ξ)对应的矩阵形式每行组成一次实现中的随机变量向量，每列为同一随机变量在不同实现中的取值，各列相互独立并且满足正态分布。对于高斯随机场，其中的独立随机变量Zi(ξ)仍为高斯模型，并且其数学期望满足条件

(4)

在二维区域，特征函数{φi(x)}满足以下条件

(5)

式中:Ω为二维闭合区域；x和y为二维区域坐标；δij为K-delta函数。

展开式(3)中特征值{λi}的解析解为[10]

(6)

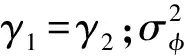
计算过程中，对于特征值{λi}与特征函数{φi(x)}，可通过求解第二类Fredholm方程得到[11]

(7)

式中:C(x1,y1;x2,y2)为二维随机场协方差函数，其表达式为

(8)

其中|x1-x2|与|y1-y2|为二维随机场样本点距离。当式(3)成立时，可将协方差函数用以下谱展开形式表示

(9)

同时，实际计算中可取M阶截断，用模拟值近似表达理论协方差函数的结果为

(10)

在所述处理的基础上，对于多维随机变量的协方差函数可建立其对应的矩阵关系，其表达式为

(11)

在利用以上建立的方法进行求解后，为进行误差分析，可利用不同展开阶数分析特征值λi(i=1,2,…,L)的变化趋势，分析阶数在整个K-L展开中的权重。也可利用协方差计算结果进行误差分析，当式(10)成立时，将M阶展开的协方差计算结果与理论协方差函数式(8)的结果进行对比，可得到协方差、相关长度、展开阶数的相互关系。

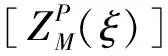
(12)

2 钻柱动力学模型

在完成井壁摩擦随机性研究的基础上，进行钻柱动力学分析，根据图1所示的受力分析模型，建立基于井壁随机摩擦的水平钻柱振动分析模型[12]

(13)

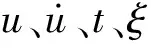
要进行振动方程的求解，首先需要确定各个力的表示方法。前面已给出摩擦力的描述与处理方法，此处确定其他相关各力求解方法与表达式。

对于Fsta(x,t)，其求解表达式为

Fsta(x,t)=Fstaδ(x)

(14)

式中:Fsta为Fsta(x,t)的振幅；δ(x)为对应于分析点位移的狄拉克δ函数。

对于Fhar(x,t)，其对应的求解公式为

Fhar(x,t)=F0sin(ωft)δ(x-L)

(15)

式中:F0为Fhar(x,t)的谐振力振幅；ωf为转动角速度；Fhar(x,t)的振动平衡位置对应为x=L，以及由此定义的狄拉克函数δ(x-L)。

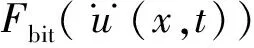
(16)

式中:C1为针对机械钻速ROP确定的系数；C2为描述岩石与钻头非线性特性的系数。

对于牙轮钻头，根据钻头与岩石接触处的边界条件，确定其计算公式为[14]

(17)

(18)

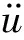
在完成各力的描述以及确定其求解方法的基础上，为进行钻柱动力学模型求解，进行模型离散求解方法研究。考虑钻柱在井下的工况条件，建立离散分析模型，将钻柱离散为n个单元，每个单元长度为l，对应的质量分别为m1，m2，…mn-1，mn,其结果如图2所示。对应于式(13)中的质量矩阵、阻尼矩阵与刚度矩阵，可分别得到其离散结果。其中，质量矩阵的表达式为

(19)

刚度矩阵的表达式为

(20)

阻尼矩阵的表达式为[15]

[C]=α[M]+β[K]

(21)

其中α，β为比例系数，可利用实验测试与仿真进行确定。

图2 动力学求解离散方法与模型Fig.2 The discrete method and model of dynamics solving

3 试验测试与基本参数

为验证理论模型的准确性及进行关键参数的影响分析，进行试验测试与算例分析。与试验模型对应，确定进行算例分析的相关输入参数，对比分析测试结果与理论计算结果。并且在此基础上，进行关键参数对钻柱动力学特性的结果影响分析。钻井综合试验平台，如图3所示。将台架放置最大倾斜位置，选取造斜后的水平钻进段进行测试。在钻头位置布置测试点1，在距离钻头60 m处布置测试点2，其对应的井下工况,如图4所示。

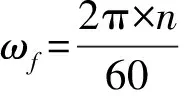
图3 钻井综合试验平台实验测试Fig.3 Experimental test of drilling comprehensive platform

图4 与试验测试对应的模型Fig.4 The analysis model corresponding to experimental test

4 算例分析

试验测试中，由于井身结构的特点，不能测试井壁摩擦因数，同时也不方便得到稳定的振动位移值。同时，为了对比分析相同条件下的试验测试与算例结果，借助前面的基本参数为输入参数，进行算例求解与分析。首先，利用建立的理论模型，进行井壁摩擦随机场分析，得到井壁摩擦因数的模拟结果，如图5(a)所示。然后利用建立的钻柱动力学模型与求解方法，求解算例模型的钻柱动力学结果，得到钻柱在测试点1处的振动位移结果,如图5(b)所示。由图5可得，钻进过程中，井壁摩擦因数与测试点处的位移均呈现出明显的随机特性，而且算例中的振动位移，相对于钻进的进尺而言比值较小。

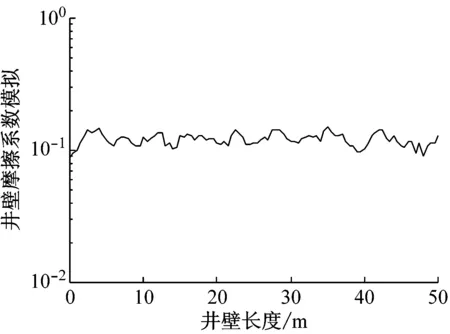
(a) 随机摩擦因数模拟

(b) 钻头纵向位移图5 摩擦力场与振动位移Fig.5 The friction force and vibration displacement

由于测试点位移与进尺的比例关系，进行振动位移对比效果不明显。为对比不同方法的结果，对测试点处的振动速度进行分析，包括实际测试、井壁摩擦随机、井壁定摩擦的振动速度结果，如图6所示。由图6可知，测试得到的振动速度均值都在1.3 mm/s附近，考虑摩擦随机性的振动速度值与实验测试结果相似，变化范围大致为1～1.8 mm/s，而且呈现出明显的随机性特性，而定摩擦结果变化范围为1.27～1.33 mm/s，振动速度具有周期性变化特点。算例结果中，利用随机摩擦模型得到振动速度特性更接近测试结果，更能反映测试点处真实运动特性，验证了理论分析的准确性。同时也说明，在深井、超深井的水平钻进，或者靶径值较大的新型油气资源开采中，更需要关注井壁摩随机性对钻柱动力学特性的影响。

(a) 随机摩擦的振动速度

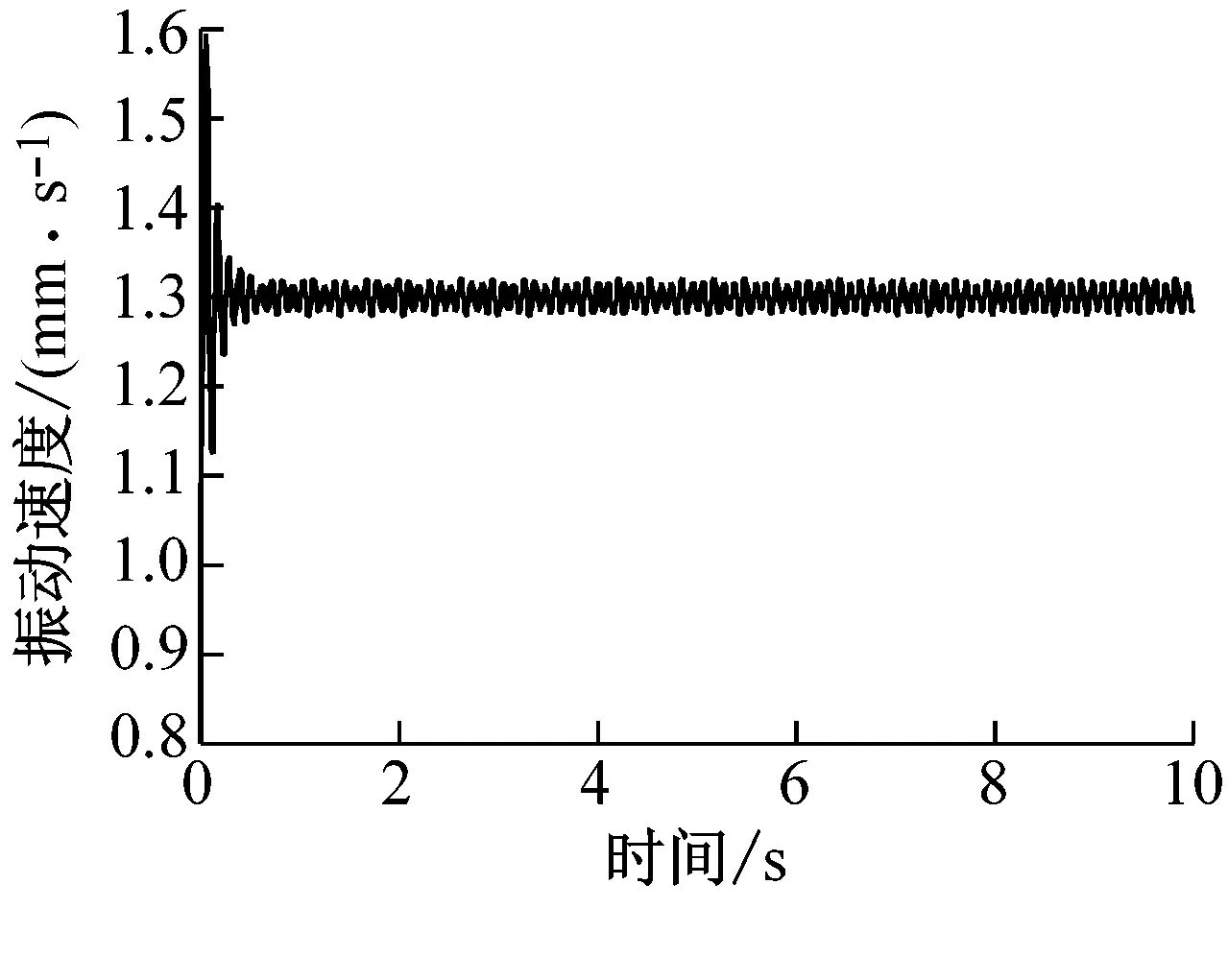
(b) 定摩擦的振动速度

(c) 实验测试的振动速度图6 测试点1处的振动速度Fig.6 The vibration velocity of point No.1

通过以上的测试与计算结果的对比，验证了计算方法的准确性与可靠性，因此根据建立的理论模型进行算例分析。首先，进行前面计算得到的振动速度频谱分析，根据试验测试条件与算例参数，取对应转速为100 r/min的速度值进行分析结果,如图7所示。由图7可知，频谱分析结果中，由于井壁摩擦力的随机性，其对钻柱振动速度的频谱结果有一定的影响。但整体而言，算例中钻井平台的动力输入转速对振动速度的影响最大，此处表现为100 r/min以及其整数倍。

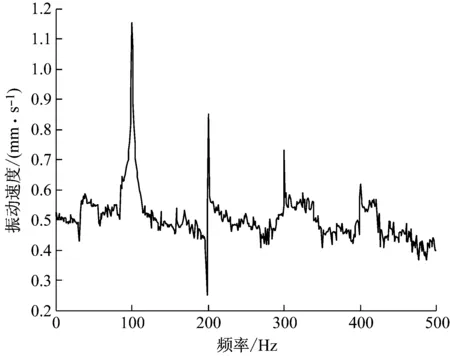
图7 钻柱振动速度的频谱分析结果Fig.7 The spectrum analysis result of drill string vibration velocity

为了分析钻进过程中的功耗与效率，定义效率公式为

(22)

求得效率结果,如图8所示，钻进过程中钻柱振动导致对应的力、速度发生变化，井壁摩擦随机性导致效率结果也呈现出一定的随机波动，其平均值约为0.25。

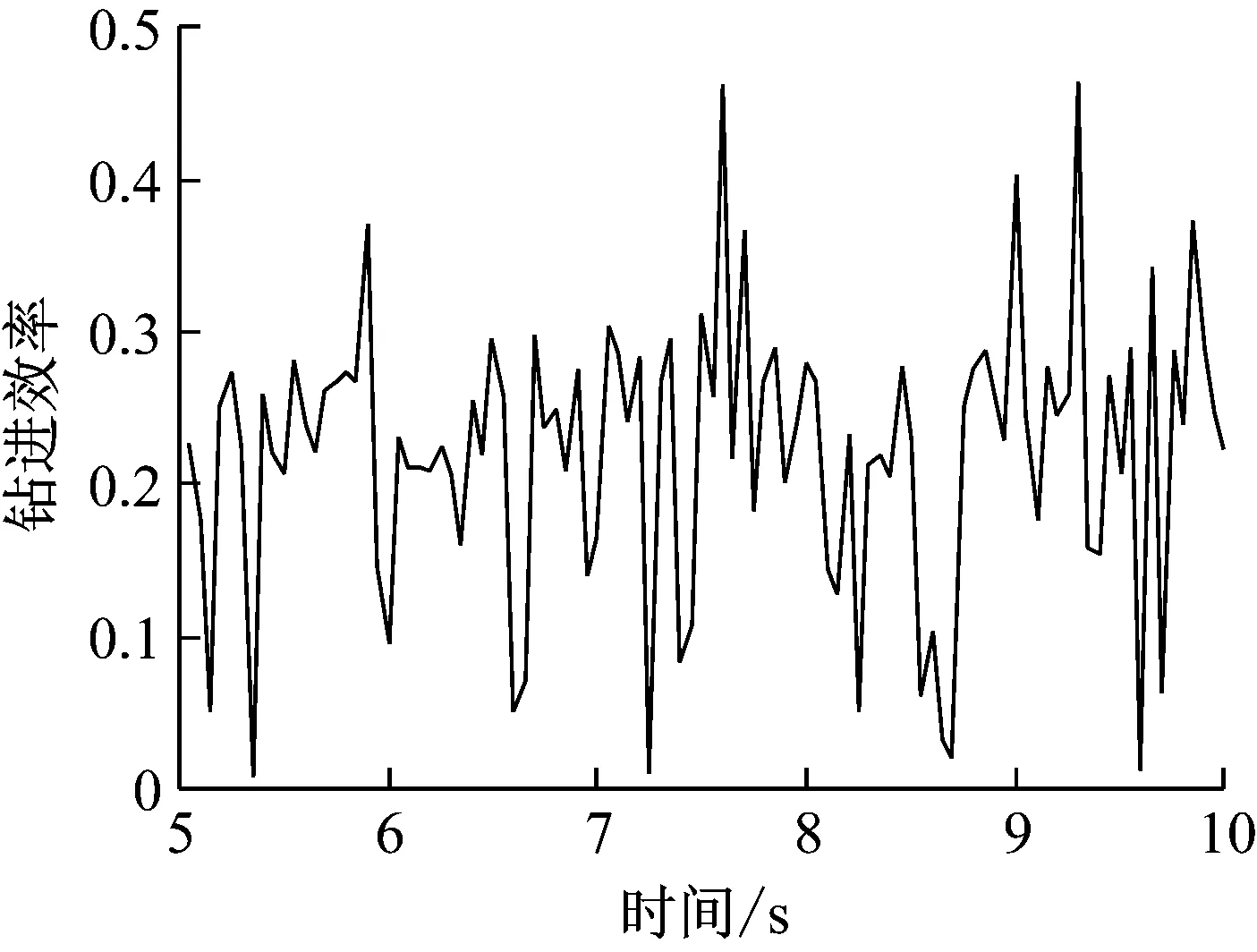
图8 钻进效率Fig.8 The drilling efficiency

对于油气井生产过程，钻井效率具有重要的实际意义，为进一步确定效率的分析结果，进行效率的均方值分析，其求解方法如式(23)所示。代入前面求解得到的效率值，设置不同的求解次数nη的结果,如图9所示。由图9可知，虽然效率变动值范围较大，但是随着求解次数的增加，平均功率值迅速稳定集中在某值。以算例结果为例，其迭代次数>200时，其迅速集中在约0.057。

(23)

对于其他关键参数对钻柱动力特性的影响，结合油气生产现场实际情况，影响振动特性的关键参数包括钻柱长度、井壁摩擦圆长径、机械转速等，可以利用以上求解方法与步骤，变换相关参数，得到相关结果并完成相关分析。

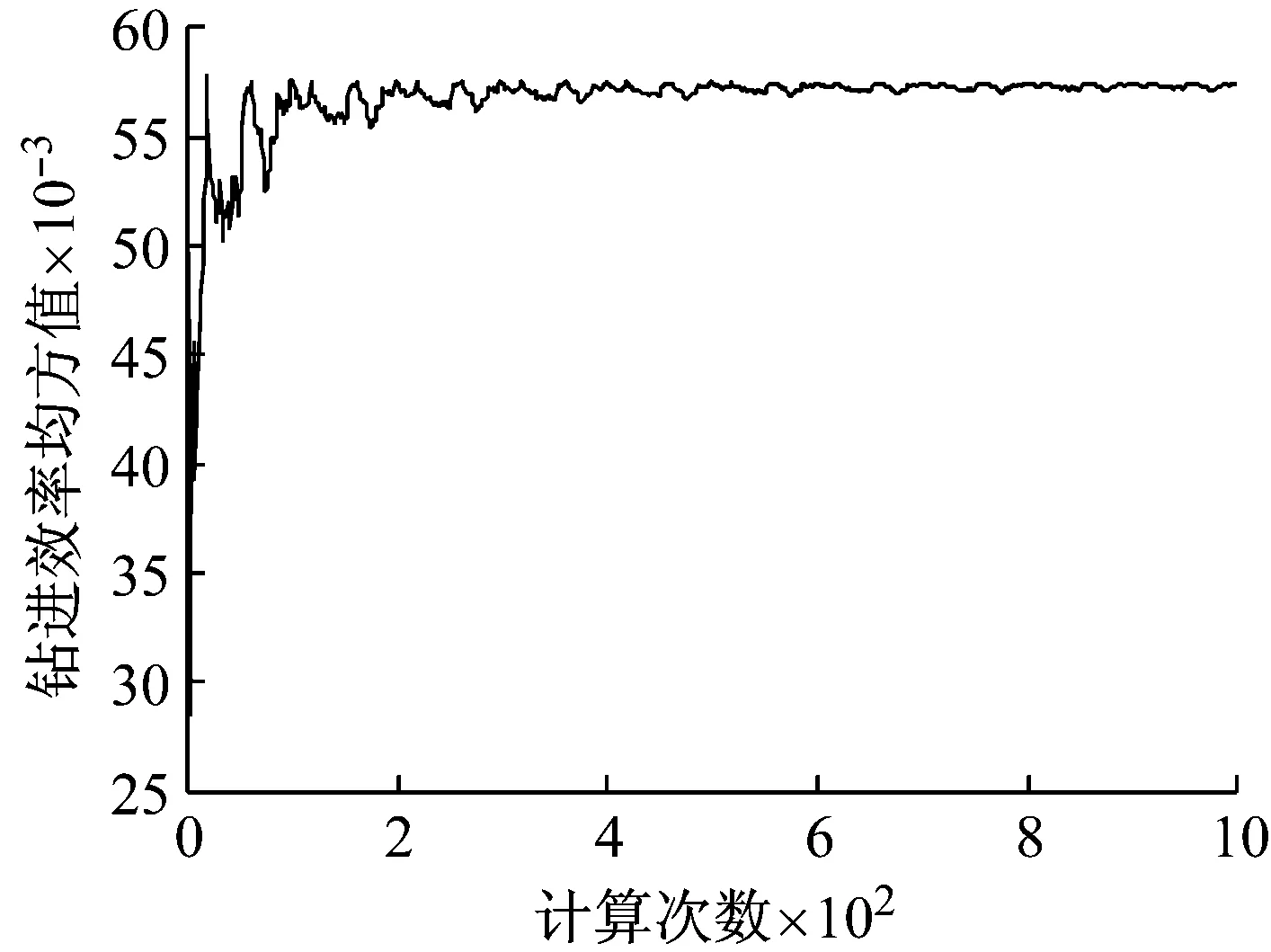
图9 钻进效率的均方值Fig.9 The mean-square value of drilling efficiency

5 结 论

(1)针对现有新型油气资源的开采条件，特别是页岩气、煤层气、大位移水平井等，井壁摩擦对钻柱动力学的影响具有越来越重要的影响。只有考虑钻柱井壁摩擦随机性，才能准确评价钻柱动力学特性。对于新层位、新地质构造、新井身结构的油气资源钻井条件，需要综合大量的现场数据与实验测试，才能准确描述井壁摩擦随机性，保证基础输入参数与求解结果的可靠性。

(2)文章结合实际井下工况，描述井壁摩擦随机性，以及给出构建井壁随机场的步骤与方法，以此为基础，建立水平钻柱动力学求解模型。根据实验测试确定基本输入参数，进行算例分析，得到振动求解和效率分析结果。建立的研究方法，可为基于井壁摩擦随机性的钻柱动力学分析，以及关键参数对钻柱动力学的影响定量评价提供参考。

(3)钻柱动力学是油气资源生产过程井下工具安全生产、提高破岩效率的理论基础。同时，通过工具失效、破岩等结果参数，可以反推对应的钻柱动力学计算方法是否合理。只有与工具失效、破岩等结果参数反推的钻柱动力学结果相吻合，才能满足实际需要，有效促进相关领域技术发展。

参 考 文 献

[1] XUE Q, WANG R, LIU B, et al. Dynamic measurement of spatial attitude at bottom rotating drillstring: simulation, experimental, and field test[J]. Journal of Energy Resources Technology, 2016,138(2):022903.

[2] GHASEMLOONIA A, RIDEOUT D G, BUTT S D. A review of drillstring vibration modeling and suppression methods[J]. Journal of Petroleum Science and Engineering,2015, 131: 150-164.

[3] KAPITANIAK M, HAMANEH V V, CHAVEZ J P, et al. Unveiling complexity of drill-string vibrations: experiments and modelling[J]. International Journal of Mechanical Sciences,2015,101: 324-337.

[4] 赵丽娟, 田震. 薄煤层采煤机振动特性研究[J]. 振动与冲击, 2015, 34(1):195-199.

ZHAO Lijuan,TIAN Zhen. Vibration characteristics of thin coal seam shearer[J]. Journal of Vibration and Shock,2015,34(1):195-199.

[5] YANG M, LI X, DENG J, et al. Prediction of wellbore and formation temperatures during circulation and shut-in stages under kick conditions[J]. Energy, 2015,91: 1018-1029.

[6] ALBDIRY M T, ALMENSORY M F. Failure analysis of drillstring in petroleum industry: a review[J]. Engineering Failure Analysis, 2016,65: 74-85.

[7] MONGKOLCHEEP K, RUIMI A, PALAZZOLO A. Modal reduction technique for predicting the onset of chaotic behavior due to lateral vibrations in drillstrings[J]. Journal of Vibration and Acoustics, 2015,37(2): 021003.

[8] 靳红玲, 陈建军, 赵宽,等. 含随机参数的空间柔性梁动力学模型[J]. 振动与冲击, 2014,33(14):6-10.

JIN Hongling, CHEN Jianjun, ZHAO Kuan, et al. Uncertainty dynamic modeling of spatial flexible beam with probabilistic parameters[J]. Journal of Vibration and Shock, 2014,33(14):6-10.

[9] 张佳文, 郭文华, 项超群. 基于协方差本征变换与谐波合成法的随机风场模拟[J]. 振动与冲击, 2013, 32(21):197-203.

ZHANG Jiawen, GUO Wenhua, XIANG Chaoqun. Simulation of stochastic wind field based on covariance proper transformation and weighted amplitude wave superposition[J]. Journal of Vibration and Shock, 2013,32(21):197-203.

[10] YANG Jinzhong, ZHANG Dongxiao, LU Zhiming. Stochastic analysis of saturated-unsaturated flow in heterogeneous media by combining Karhunen-Loeve expansion and perturbation method[J]. Journal of Hydrology, 2004,294(1): 18-38.

[11] 刘颖, 杨绿峰, 莫远昌. 基于随机响应面法的结构可靠度研究[J]. 广西大学学报(自然科学版),2008,33(4): 366-369.

LIU Ying, YANG Lüfeng, MO Yuanchang. The structural reliability research based on the stochastic response surface method[J].Journal of Guangxi University(Natural Science Version), 2008,33(4): 366-369.

[12] RITTO T G, ESCALANTE M R, SAMPAIO R, et al. Drill-string horizontal dynamics with uncertainty on the frictional force[J]. Journal of Sound and Vibration, 2013,332(1): 145-153.

[13] DEPOUHON A, DETOURNAY E. Instability regimes and self-excited vibrations in deep drilling systems[J]. Journal of Sound and Vibration, 2014,333(7): 2019-2039.

[14] FRANCA L F P. Drilling action of roller-cone bits: modeling and experimental validation[J]. Journal of Energy Resources Technology, 2010,132(4): 043101.

[15] RITTO T G, SAMPAIO R, ROCHINHA F A. Model uncertainties of flexible structures vibrations induced by internal flows[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2011,33(3): 373-380.