一种非线性能量阱的构建及瞬态特征分析
刘海平, 王耀兵 (1. 北京空间飞行器总体设计部,北京 100094;2. 空间智能机器人系统技术与应用北京市重点实验室,北京 100094)
传统的吸振技术主要通过将线性动力吸振器或者调谐质量阻尼器与主振结构连接实现。当主振系受简谐激励时,通过调整线性动力吸振器的固有频率与简谐激励频率一致即可实现有效抑振[1-5]。实际中,任何激励载荷都不可能仅由单一频率组成,而线性动力吸振器窄带频率保持特性极大限制了其在工程中的应用。
非线性动力吸振器由于其宽频特征被认为是替代线性动力吸振器的有效方法之一[6-11]。近年,非线性能量阱作为一类新型非线性动力吸振器得到广泛的关注与研究[12-14]。相比而言,非线性能量阱与常规非线性动力吸振器最大的区别在于缺少线性刚度项。然而,实际中构建纯立方刚度非线性能量阱困难极大,只能尽量减小线性刚度的影响。
卫星在地面发射阶段,受到来自运载火箭点火及火工连接装置爆炸解锁瞬间产生的冲击载荷的影响,对星载电子设备构成极大威胁[15-17]。本文以抑制主动发射段,卫星结构板上星载设备受到来自运载火箭瞬态载荷的影响为目标,探索采用单根欧拉梁构建具有实用价值的非线性能量阱。通过建立安装非线性能量阱的系统动力学模型,对非线性能量阱发生靶能量传递的阈值特征,以及不同初始输入能量下非线性能量阱和线性主振系的响应特征和能量迁移特征进行了计算研究。相关理论成果可用于指导后续的实验验证并为工程应用奠定基础。
1 非线性能量阱构建
非线性能量阱(Nonlinear Energy Sink)因其在一定输入能量下可发生单向不可逆的靶能量传递而被广泛关注。目前,大部分相关研究利用立方刚度元件构建非线性能量肼,其特点主要表现为小质量、线性刚度为零、弱阻尼和纯立方刚度(本质非线性刚度)。按照如上标准,构建一个纯立方刚度的非线性系统难度较大,实际设计中只能尽可能将线性刚度项减小、立方刚度弹性元件不承载、减少各部分结构可能引入的阻尼。
本文考虑采用单根欧拉梁作为非线性刚度元件,两端固支;在欧拉梁中间位置连接吸振子,使用导轨支承吸振子质量并约束其运动方向;为了减小欧拉梁线性刚度的影响,可通过调整两端的压缩量使其产生屈曲变形,如图1所示。为了证明以上所提非线性能量阱的设计方案合理可行,以下对其力学特性进行分析研究。

图1 非线性能量阱结构示意图Fig.1 Schematic of the nonlinear energy sink
单根欧拉梁受端部压缩载荷作用的变形,如图2所示。其中,单根梁两端施加的压缩载荷可以由变形势能得到。

图2 单根欧拉梁变形示意图Fig.2 Schematic of a single Euler beam under force
由图2可知,在压缩载荷P作用下,单根梁纵向受载变形量为ux。其中,l0为未受载单根梁自由长度,lc为受载变形梁的长度。单根梁内储存的势能为
(1)
式中:A为矩形截面梁的截面面积;E为材料杨氏模量。
两端固支受载变形梁的横向变形满足第1阶模态振型的形函数
(2)
式中:uy为单根梁中点的横向载荷Ft作用下的位移;x为单根梁沿纵轴方向的长度。
受载变形梁在横向载荷作用下的长度减小量等于受载变形梁的弧长变化量。利用弧长公式,得到
(3)
根据文献[18]给出的近似计算方法,由弧长公式(3)可化简得到弧长表达式
≅

(4)
综合式(3)和式(4),满足近似计算的条件是πuy/lcsin(2πx/lc)≈0,即:x≈lc(ux< 由受载变形梁在横向载荷作用下的弧长公式(4)减去受载变形梁的长度lc,可以得到单根梁的长度变形量。结合未受横向载荷Ft作用,受压缩载荷变形梁的势能公式(1),得到单根梁内储存势能的变化量为 (5) 单根梁横向受载产生的弯曲势能 (6) 式中:I为矩形截面梁的截面惯性矩;I=bt3/12。 对式(6)积分,得到单根梁的弯曲势能为 (7) 横向载荷Ft沿横向位移uy做功等于受载变形梁在变形过程中的势能变化量 (8) 由式(8)发现,变形梁横向力Ft由线性和非线性两部分组成,引入参数k1和k3分别为线性刚度和立方刚度代入式(8),得到 (9) 式中: (10) 为了验证以上设计方案是否满足非线性能量阱要求的线性刚度近似为零和近似纯立方刚度特征。选择初始设计参数为:单根梁未变形长度l0=100×10-3m,初始压缩量ux=0,材料弹性模量E=210 GPa,矩形截面厚度t=1×10-4m,矩形截面宽度b=5×10-3m。将初始参数代入式(9)和式(10),得到力-位移曲线,如图3所示。另外,图3还给出式(9)仅保留立方刚度项对应的横向力-位移关系曲线。可见,线性刚度对单根欧拉梁输出刚度影响较小,两条曲线几乎一致。对应以上设计参数的刚度分别为:k1=17.05 N/m,k3=1.28×109N/m3;显然相比于立方刚度项,线性刚度的影响几乎可以忽略不计。综上所述,基于单根欧拉梁可成功构建具备近似纯立方刚度的非线性能量阱。 图3 单根欧拉梁横向力-位移关系曲线Fig.3 Relationship between horizontal force and displacement of a single Euler beam 卫星发射过程中,由于运载火箭点火和级间火工分离爆炸解锁过程中产生的瞬态冲击载荷影响将对星载高精度设备造成极大风险。如何对发射段较宽频带内的冲击载荷进行有效减缓或抑制成为衡量航天器性能的一项关键指标。本部分以安装在卫星结构板上有效载荷为对象,利用第1节构建的非线性能量阱对星载设备在瞬态冲击载荷作用下的响应进行控制。 图4给出卫星结构板上安装非线性能量阱的示意图,相应的系统动力学模型也在图上给出。实际中,设备安装在铝蜂窝夹层结构板上。为了便于分析计算,将铝蜂窝夹层结构板简化为等效刚度ks和集中质量ms,相应结构板阻尼为cs;星载设备等效为集中质量md,刚度kd和阻尼cd;非线性能量阱则包括集中质量mNES,非线性刚度kNES和阻尼cNES。其中,非线性刚度kNES由线性刚度k1和立方刚度k3组成参见“1”节。 图4 安装非线性能量阱系统模型Fig.4 Schematic of a systematic model with a nonlinear energy sink 根据图4模型建立系统动力学方程 (11) 因此,结构板-星载设备-非线性能量阱系统的初始输入能量为 (12) 星载设备储存的动能和势能之和为 (13) 非线性能量阱储存的总能量为 (14) 结构板储存的总能量为 (15) 系统总能量为 E(t)=Es(t)+Ed(t)+ENES(t) (16) 为了评估非线性能量阱是否发生靶能量传递,定义非线性能量阱瞬时能量比 (17) 为了评估非线性能量阱对初始输入能量的耗散能力,定义非线性能量阱瞬时耗能比 (18) 为了便于计算,选择系统各部分设计参数如下。 结构板:质量ms=10 kg,弹簧刚度ks=1×107N/m,阻尼系数cs=5 N·s/m;设备:质量md=6 kg,弹簧刚度kd=5×106N/m,阻尼系数cd=1 N·s/m;非线性能量阱:质量mNES=0.05 kg,阻尼系数cNES=1 N·s/m,未变形长度l0=100×10-3m,其他参数详见“1”节。 图5 非线性能量阱耗散能量与系统初始速度关系曲线;实心圆为四个仿真计算工况 Fig.5 Percentage of the dissipated energy as a function of the initial displacement; solid circles refer to four simulations 以下给出四种不同初始输入能量的仿真分析结果。首先,输入较小量级的初始能量(工况A)Eint=1.3 J,计算结果,如图6所示。由图6可知,各部分结构以主振系统的固有频率振动,非线性能量阱对系统的振动抑制贡献很小,大部分能量仍然局限在主结构上。 表1 不同初始输入条件抑振效果Tab.1 The dissipated energy percentages forthe different simulations 第2个计算工况输入能量增加到Eint=45 J,计算结果,如图7所示。由图7可知,在该输入量级下,非线性能量阱发生靶能量传递。在0~0.5 s时段内,非线性能量阱的吸振子响应幅值显著,并使能量向非线性能量阱转移;在0.5~2 s时段内非线性能量阱经历了缓慢的衰减过程;并在约2 s附近时段能量局限于非线性能量阱;在>2 s时段,能量再次流回线性主振系。 (a) 位移响应 (b) 瞬时能量比图6 工况A仿真结果,非线性能量阱━ ━,结构板┅┅,设备━·━ Fig.6 Simulation results for case A, nonlinear energy sink━ ━,structural plate┅┅,equipment━·━ (a) 位移响应 (b) 瞬时能量比图7 工况B仿真结果,非线性能量阱━ ━,结构板┅┅,设备━·━ Fig.7 Simulation results for case B, nonlinear energy sink━ ━,structural plate┅┅,equipment━·━ 图8给出初始输入能量Eint=125 J时的计算结果。在开始阶段各部分响应表现出一个非线性拍特征,非线性能量阱的响应在约0~1 s和4~4.5 s时段内占优。初始输入能量继续增加到Eint=320 J时虽然非线性能量阱位移响应幅值更大,但是非线性能量阱瞬时能量比降低。 (a) 位移响应 (b) 瞬时能量比图8 工况C仿真结果,非线性能量阱━ ━,结构板┅┅,设备━·━Fig.8 Simulation results for case C, nonlinear energy sink━ ━,structural plate┅┅,equipment━·━ 为了对以上各工况仿真计算结果的频率特征进行研究,对相对位移(ys~yNES)采用Morlet小波基的小波变换得到时程响应数据中频谱含量随时间变化的特征,如图10所示。由图10可知,输入能量较小时,振动局限于线性主振系统,并未发生能量向非线性能量阱流动的特征参见图10(a),主要频谱集中在约100 Hz和180 Hz附近。随着能量增加,越过了激发非线性能量阱靶能量传递的阈值,在高频约100~200 Hz范围内并未见到工况A对应在180 Hz频点的线谱,取而代之的是一个宽频谱带。输入能量继续增加,虽然激发了非线性系统较多高频分量,但是能量仍然集中在约100 Hz和180 Hz线谱附近,如图10(c)和图10(d)所示。 为了验证本文所建理论模型和分析结果的有效性,正在开展地面验证试验,相关结果将另文详述。 (a) 位移响应 (b) 瞬时能量比图9 工况D仿真结果,非线性能量阱━ ━,结构板┅┅,设备━·━Fig.9 Simulation results for case D, nonlinear energy sink━ ━,structural plate┅┅,equipment━·━ (a)工况A(b)工况B(c)工况C(d)工况D 图10 相对位移响应(ya~yNES)小波变换 Fig.10 The wavelet transform of the relative response (ya—yNES) 以实现有效抑制星载设备在主动发射段瞬态冲击载荷为目标,提出一种基于单根欧拉梁的非线性能量阱,通过对比研究表明:两端固支单根欧拉梁输出刚度由线性刚度和非线性立方刚度组成,且与纯立方刚度相比其线性刚度的影响几乎可以忽略。 根据实际星载设备安装条件,建立结构板-设备-非线性能量阱系统动力学模型。通过数值计算对比研究不同初始输入条件下非线性能量阱的振动抑制效果。研究表明: (1) 非线性能量阱发生靶能量传递存在初始能量阈值; (2) 当输入能量跨过阈值时,振动能量发生从线性主振系向非线性能量阱发生靶能量传递; (3) 即使初始输入能量跨过阈值,如果输入能量过大也不能有效激发非线性能量阱的靶能量传递特征。 综合以上研究表明单根欧拉梁构建的非线性能量阱可以有效抑制星载设备在发射段瞬态冲击载荷的影响,改善设备的力学环境。 参 考 文 献 [1] FRAHM H. Device for damping vibrations of bodies: US Patent. 989.958[P].1909-10-30. [2] ORMANDROYD J, DEN HARTOG J P. The theory of dynamic vibration absorber[J]. Transaction of American Soceity of Mechanial Engineering, 1928, 50: 9-22. [3] 王现成, 郭蓬勃, 张益民, 等. 用吸振器消除框架梁横向振动的可行性[J]. 振动与冲击, 2015, 34(14): 179-182. WANG Xiancheng, GUO Pengbo, ZHANG Yimin, et al. Feasibility of absorbing the transverse vibration of a frame-beam induced by attached oscillating equipment by using a vibrational absorber[J]. Journal of Vibration and Shock, 2015, 34(14): 179-182. [4] 杨飞, 杨智春, 王巍. 吸振夹层壁板颤振抑制的吸振器频率设计[J]. 振动与冲击, 2009, 28(7): 65-68. YANG Fei, YANG Zhichun, WANG Wei. Frequency design of dynamic vibration absorber for flutter suppression of sandwich panel[J]. Journal of Vibration and Shock, 2009, 28(7): 65-68. [5] 徐振邦, 吴清文. 吸振器底座对减振效果的影响研究[J]. 振动与冲击, 2014, 33(13): 72-76. XU Zhenbang, WU Qingwen. Influence of the base of vibration absorber on vibration attenuation effect[J]. Journal of Vibration and Shock, 2014, 33(13): 72-76. [6] PIPES L. Analysis of a nonlinear dynamic vibration absorber[J]. Journal of Applied Mechanics, 1953, 20: 515-518. [7] ARNOLD F R. Steady state behaviour of systems provided with nonlinear dynamic vibration absorbers[J]. Journal of Applied Mechanics, 1955, 22: 487-492. [8] 刘海平, 杨建中, 罗文波, 等. 新型欧拉屈曲梁非线性动力吸振器的实现及抑振特性研究[J]. 振动与冲击, 2016, 35(11): 155-160. LIU Haiping, YANG Jianzhong, LUO Wenbo, et al. Realization and vibration suppression ability of a new novel Euler buckled beam nonlinear vibration absorber[J]. Journal of Vibration and Shock, 2016, 35(11): 155-160. [9] 楼京俊, 唐斯密, 朱石坚, 等. 改进的本质非线性吸振器宽频吸振系数域研究[J]. 振动与冲击, 2011, 30(6): 218-222. LOU Jingjun, TANG Simi, ZHU Shijian, et al. Parametric range of improved essentially nonlinear absorber on broad frequency band[J]. Journal of Vibration and Shock, 2011, 30(6): 218-222. [10] 唐斯密, 朱石坚, 楼京俊. 非线性吸振器刚度调整策略研究[J]. 武汉理工大学学报, 2011, 35(1): 163-166. TANG Simi, ZHU Shijian, LOU Jingjun. Study on the tactic of adjusting stiffness of the nonlinear dynamic vibration absorber[J]. Journal of Wuhan University of Technology, 2011, 35(1): 163-166. [11] 罗尧, 王慧. 非线性弹簧阻尼减振装置的探究[J]. 物理与工程, 2011, 21(5): 13-16. LUO Yao, WANG Hui. Study of the nonlinear damping spring shock absorbers[J]. Physics and Engineering, 2011, 21(5): 13-16. [12] VAKAKIS A F, GENDELMAN O. Energy pumping in nonlinear mechanical oscillators: part Ⅱ—resonance capture[J]. Transactions of the ASME, Journal of Applied Mechanics, 2011, 68: 42-48. [13] GENDELMAN O, MANEVITCH L, VAKAKIS A F, et al. Energy pumping in nonlinear mechanical oscillators: part Ⅰ—dynamics of underlying Hamiltonian systems[J]. Transactions of the ASME, Journal of Applied Mechanics, 2001, 68: 34-41. [14] KREMER D, LIU K F. A nonlinear energy sink with an energy harvester: transient responses[J]. Journal of Sound and Vibration, 2014, 333: 4859-4880. [15] 马兴瑞,韩增尧. 卫星与运载火箭力学环境分析方法及试验技术[M]. 北京:科学出版社, 2014. [16] JOHNSON C D, WILKE P S, PENDLETON S C.Recent launches using the soft ride whole-spacecraft vibration isolation system[C]//AIAA Space 2001 Conference and Exposition. Albuquerque, NM, 2001: 1-10. [17] MALY J R, FOWLER E C, BISKNER A C. Structural models and dynamic measurements of satellite launch adapter structures[C]//Proceedings of 50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Palm Springs, CA, 2009: 1-12. [18] VANGBO M. An analytical analysis of a compressed bistable buckled beam[J]. Sens Actuators A, 1998, 69(3): 212-216.


2 安装非线性能量阱系统模型



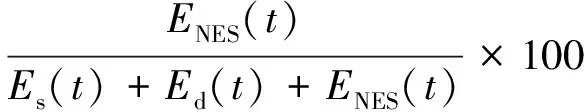

3 仿真计算及分析











4 结 论

