仿古建筑钢框架结构拟动力试验及静力推覆分析

薛建阳， 戚亮杰， 葛鸿鹏， 刘祖强(. 西安建筑科技大学 土木工程学院， 西安 70055； . 中国建筑西北设计研究院有限公司， 西安 7008)

中国古建筑凝聚了我国古代历史、科技、文化及宗教等发展成果，孕育了宝贵的民族文化和民族精神，但是由于木结构建筑受到材料(木材)自身的限制，如易翘曲、易燃、易腐朽老化等特点，使得现存木结构古建筑处于结构体系破坏、险情不断发展甚至潜伏倒塌的危险状态[1]，因此，运用其他新型材料建造的仿古建筑对继承这些历史文化遗产有着至关重要的意义。仿古建筑体系应用现代科学技术，使结构的抗灾害能力显著增强，已逐渐融入到我国建筑行业的各个领域，尤其广泛应用于全国各地的地标建筑和风景园林当中[2]，如采用钢结构建造的大明宫丹凤门、长安塔及洛阳定鼎门等均已成为当地的标志性建筑，图1为某典型钢结构仿古建筑实例。钢结构仿古建筑结构外观类似古建筑形式，与一般框架建筑造型相差较大，如挑檐较大，在屋架构件与柱架结构之间存在斗拱层等。但由于仿古建筑采用的建筑材料、节点连接方式与木结构差异较大，故结构受力特点及分析方法与木结构古建筑有很大区别[3]。

图1 典型钢结构仿古建筑Fig.1 Typical steel archaized buildings

国内外对框架结构体系的研究主要是针对框架-支撑结构体系、钢框排架结构体系[4-6]，而对仿古建筑钢框架结构体系尚无研究。仿古建筑体系独有的坡屋顶、圆柱、斗拱等构件使得其整体布置较为复杂，荷载传递路径及耗能机理并不明确，且我国现行规范尚未涉及此类结构的设计条文。

目前在对钢框架结构的抗震性能研究时,由于拟静力试验方法的人为干预性较强，无法反映结构在实际地震作用下的动力响应。而振动台试验受尺寸效应等因素的影响较大，导致试验结果的失真度较高。因此，拟动力试验的运用越来越广泛，它既有拟静力试验方便简洁的特点，又可以对结构施加真实地震波，获取结构体系在地震作用下真实的动力响应[7]。

为了了解传统风格结构钢框架体系在真实地震波作用下的抗震性能，本课题组在已完成的钢结构仿古建筑异型节点受力性能研究[8-9]的基础上，以某一典型钢结构仿古建筑殿堂结构为原型，设计制作了一榀含异型节点(见图2)的仿古建筑钢框架结构，并对其进行拟动力试验，以研究此类结构的抗震性能。

图2 钢结构异型节点Fig.2 Steel special-shaped joint

1 试验概况

1.1 模型设计与制作

受试验场地条件的限制，结构缩尺比取为1/2，模型构件在工厂加工制作完成后，现场拼装，模型立面及细部构造，如图3所示。除柱底与地梁采用螺栓连接外，其余均采用全焊连接。由于仿古建筑使用空间要求的规定，正厅大梁(L1)采用225 mm×125 mm的箱形截面，偏厅侧梁(L2)采用150 mm×100 mm的焊接箱形截面形式，两梁连接处形成一异型节点(见图2)。构件截面尺寸，如表1所示。钢材等级取为Q235B，采用E43型焊条手工焊，钢材材性试验结果，如表2所示。

图3 试件几何尺寸及构造(mm)Fig.3 Dimensions and details of specimens(mm)

表1 结构构件参数表Tab.1 Main parameters of specimens

表2 钢材的材性Tab.2 Material properties of steel

1.2 相似关系

为了满足模型与原型结构的质量与配重的相似关系[10]，将屋面均布荷载分别等效换算为沿柱Z1-1、Z3-1、Z3-2、Z2、Z1-2顶部施加的竖向集中荷载。考虑到坡屋顶的特殊构造及加载时的安全因素，通过外悬挂混凝土块的方式对结构施加配重；线长度相似系数取为1/2，其余结构动力相似关系，如表3所示。

1.3 试验原理

拟动力试验由计算机进行数值分析并控制加载，即给定地震波加速度时程记录，由计算机计算当前一步的反应位移，同时测量结构对于该步位移的实际恢复力，并反馈给计算机，计算机再根据实测的恢复力和其他已知参数计算下一步的位移反应。其动力微分方程可表示为

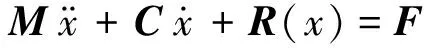
(1)

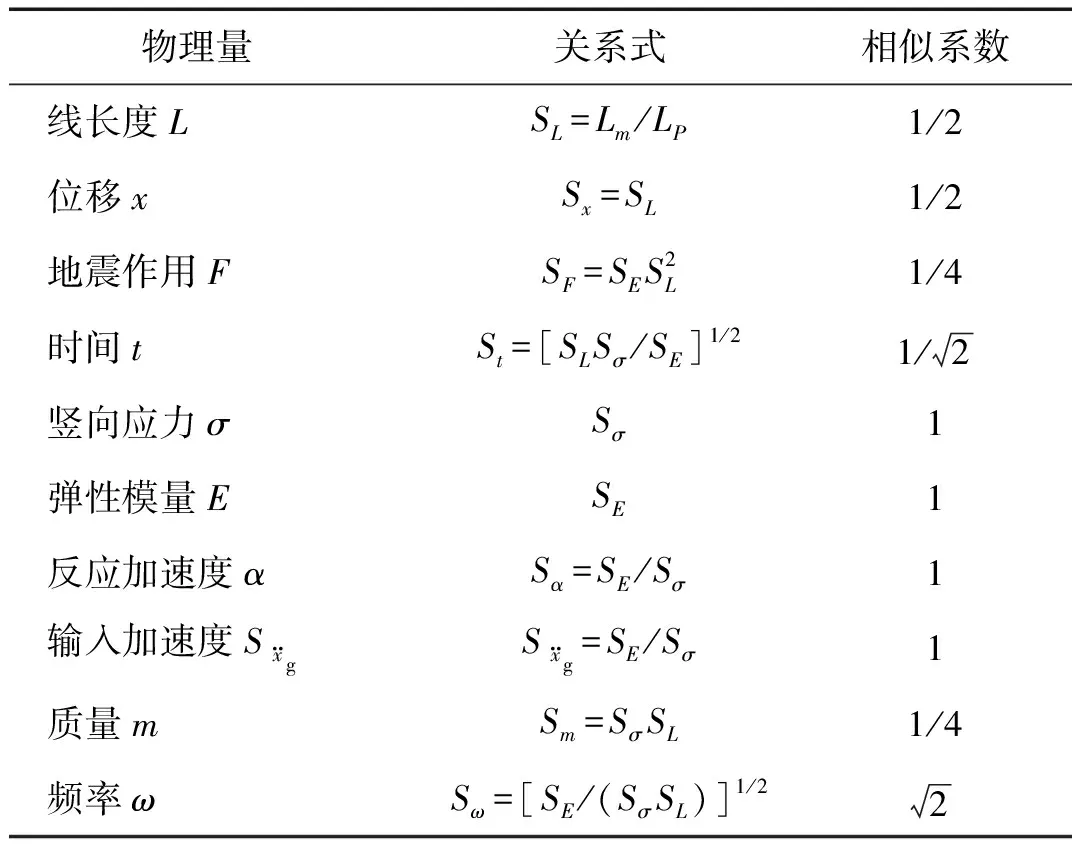
表3 动力相似关系Tab.3 Dynamic similitude relations

求解采用中心差分法，即将上述的微分方程转化为差分的形式，当时间步长为Δt时，速度及加速度分别为

(2)

(3)

1.4 加载方案

试验加载方法参考建筑抗震试验方法规程：JGJ 101—1996，加载在西安建筑科技大学结构工程与抗震教育部重点实验室完成，在标高2.420 m处布置一台MTS电液伺服作动器施加水平荷载，试验数据由TDS602数据采集仪采集并记录。为了防止试件平面外发生失稳现象，在大梁L1处每间隔1 m布置一块方形侧板，平面外两侧由滑轮支撑夹紧，保证结构平面内的稳定[11]，整体框架模型，如图4所示。试验时首先在Z1-1、Z3-1、Z3-2、Z2、Z1-2柱构件处分别施加7.8 kN、13.4 kN、9.4 kN、7.1 kN和5.6 kN的配重，试验前测得结构的初始刚度，随后施加水平地震动荷载进行拟动力试验。由于试件为单层平面框架，将结构质量和配重质量集中在作动器所在的层高位置处，得到了模型结构的质量，即M=4 863 kg。此外，根据建筑抗震设计规范的要求，钢结构多层建筑的阻尼比ζ=0.04。

图4 钢框架模型Fig.4 Steel frame model

1.5 量测方案

除L1非加载侧端部布置MTS位移计外，在模型结构不同标高处安装电子位移计。在地梁上设置压梁以固定试件。为量测试验加载过程中基础底座实际的水平及竖向位移，在地梁端部布设电子百分表，测试数据由TDS-602数据采集仪自动量测并采集。分别在各节点域、梁端、柱端及斗、拱构件处对称布置电阻应变片。试验加载及位移量测装置，如图5所示。

1-反力墙；2-反力钢架；3-反力梁；4-作动器；5-压梁；6-地脚螺栓；7-电子位移计；8-百分表；9-试件

图5 加载装置

Fig.5 Test setup

1.6 地震波的选择

本试验模型的原型结构位于8度抗震设防烈度区，场地类别为II类。在选用地震波时，地震波的卓越周期尽量与结构所在场地的的谱特征一致。因此，本次试验选用El Centro波、汶川波与兰州波中包含最大加速度的一段地震记录作为输入波进行试验，对该钢框架结构模型在8种工况下的抗震性能进行研究，所采用地震波的加速度幅值依据相似关系进行调整[12]。在试验的初期阶段，分别输入三种地震波，以观察在不同地震波作用下结构的动力反应，当结构出现塑性特征后，仅输入汶川波进行试验。输入的地震波峰值加速度逐级增大，分别相当于8度多遇、8度设防、8度罕遇及9度罕遇地震作用。本试验加载步长取为0.014 1 s，加载步数为1 000步，总持时14.1 s。加载工况，如表4所示。

2 试验结果及分析

2.1 试验过程

在峰值加速度分别为70 gal、200 gal和400 gal的地震波作用下，结构构件均处于弹性工作阶段。说明在不超过8度罕遇烈度地震波作用下，结构未发生塑性变形，承载力仍相对较高。在峰值加速度620 gal的汶川波作用下，8.881 s时正厅边柱斗D1构件处达到屈服，随后在异型节点西侧的G构件处发生屈服现象。整体结构在7.714 s受到的水平荷载与大梁高度位移达到最大值，此时结构承受的基底剪力为60.93 kN，顶点位移为11.96 mm。从整体上看，模型结构在8度多遇烈度 (70 gal) 的地震波作用下，完全处于弹性状态，满足“小震不坏”的设防目标；在峰值加速度为400 gal (相当于8度罕遇地震)地震波作用下，结构未发生明显的塑性变形和破坏，实现了“大震不倒”的抗震设防目标。即使在峰值加速度为620 gal (相当于9度罕遇地震) 的汶川波作用下，结构也只是个别构件发生屈服(见图6)，整体工作性能良好，说明本次试验设计的仿古建筑钢框架结构具有抵抗超过本地区设防标准地震作用的能力，具有良好的抗震性能。此外，在整个加载过程中，实测地梁的水平及竖向位移非常小，对试验结果几乎无影响。

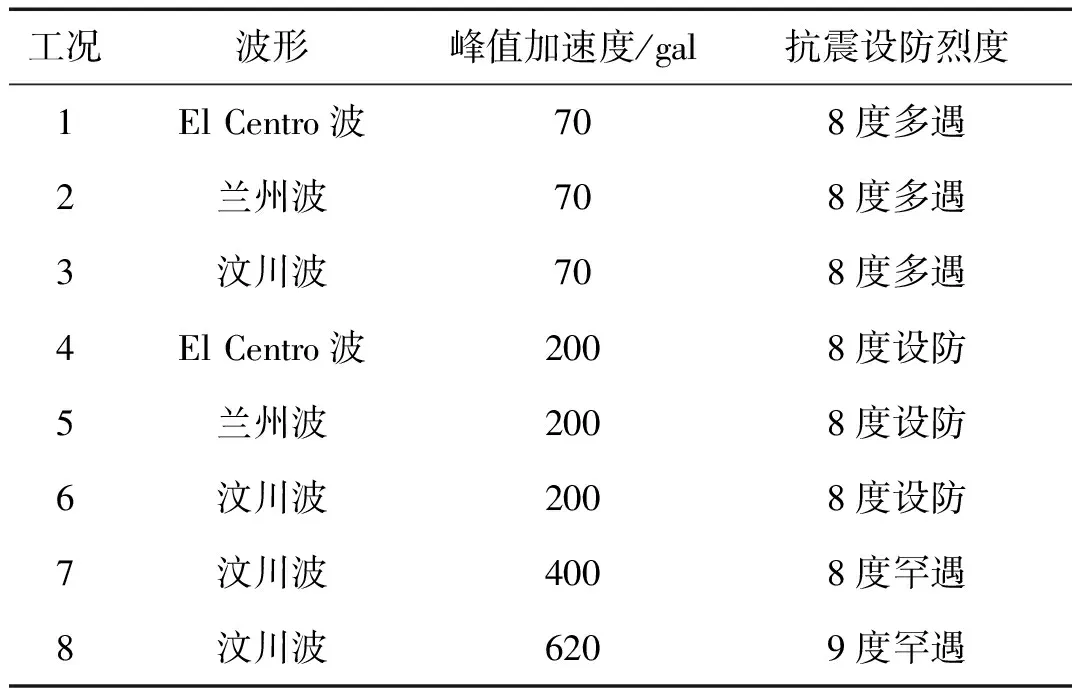
表4 拟动力试验加载制度Tab.4 Pseudo-dynamic test loading system

图6 屈服现象Fig.6 Yielding phenomenon

2.2 滞回特性

图7为该结构在拟动力加载试验中各工况下基底剪力-顶层位移滞回曲线。由图7可知，在相同加速度峰值不同地震波形的作用下，结构的滞回曲线不完全相同，表明不同地震波的频谱特性对结构的地震反应影响较大，其中兰州波对结构造成的响应最小，而汶川波作用最为明显。在70 gal、200 gal、400 gal的加载工况下，滞回曲线整体呈直线形，当荷载降低为零时，结构没有残余变形，钢框架仍处于弹性工作状态，耗能较小。随着地震波输入峰值加速度的增大，钢框架的剪力-位移响应越发明显，滞回环包围的面积也逐渐增大，结构耗能逐渐增加。在峰值加速度为620 gal的加载工况作用下，滞回曲线产生一定的残余变形，结构进入弹塑性阶段，其原因是斗D1、拱G构件的屈服使结构耗能增加，但滞回曲线仍未出现明显的捏拢现象，说明结构在9度罕遇地震的作用下仍然有较大的刚度与承载力。

(a) 工况1

(b) 工况2

(c) 工况3

(d) 工况4

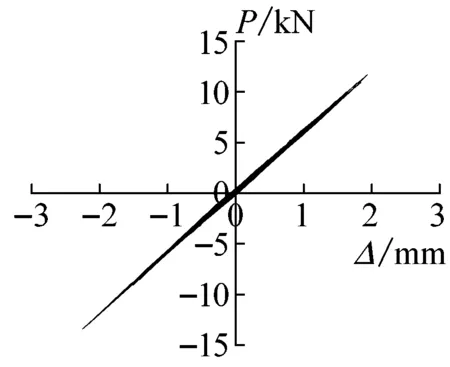
(e) 工况5

(f) 工况6

(g) 工况7

(h) 工况8图7 基底剪力-顶层位移滞回曲线Fig.7 Hysteretic loops of model

2.3 耗能性能

耗能是结构在地震波输入时吸收能量的能力，累积滞回耗能采用式(4)计算[13]

(4)

式中：Fi+1、Fi分别为第i+1点与第i点的恢复力，Xi+1、Xi分别为与其相对应的位移。图8(a)为在相同峰值加速度但不同类型地震波作用下结构的耗能对比，可以发现，施加相同峰值加速度的地震波，不同频谱特性的波形导致结构的耗能能力也不相同，说明结构耗能受加载波形的影响较大。模型结构在汶川波各个工况下的滞回耗能情况，如图8(b)所示。在峰值加速度为70 gal和200 gal的地震波作用下，累积滞回耗能较小，说明此时可恢复的弹性应变能所占比例较大，由于结构弹性应变能的增大与恢复过程交替进行，造成累积耗能时程曲线呈波浪形增加。随着输入地震波峰值加速度的增大，结构耗能逐渐上升，在9度罕遇地震波作用下，结构耗能约为8度罕遇地震波作用时约3倍，说明耗能与加载地震波幅值的增量呈非线性增加。从试验现象看出，此时结构焊缝并无开裂，说明本次试验设计的仿古建筑钢框架结构不仅可以抵抗9度罕遇地震作用，并具有较高的安全储备。

2.4 加速度响应

图9是模型结构加载点楼层处在不同工况下的加速度时程曲线。从图9 (a)可知，在不同地震波作用下，模型加速度反应时程曲线基本与其加载的地震波形相一致，但结构反应加速度与原始波形并不是同时达到极值。El Centro波、兰州波、汶川波三种波形各自的峰值加速度分别出现在1.484 s、3.514 s和8.666 s，当对结构施加200 gal的三种波形时，结构反应最大加速度分别出现在1.778 s、2.002 s和7.798 s。结构响应加速度峰值绝对值分别为407.1 gal、311.8 gal与452.8 gal，与该结构频率最为接近的汶川波对此结构的动力响应最为明显，说明频谱特性对结构的加速度响应影响显著。此外，由图9 (b)可知，在同种地震波的作用下，随着输入加速度的增大，结构的加速度响应也随之增大。在汶川波70 gal、200 gal、400 gal三种输入加速度的作用下，结构处于弹性工作状态，其时程曲线与原波形变化趋势基本一致，但随着输入加速度峰值增大，在输入620 gal汶川波的加载后期，结构时程曲线各峰值点略滞后于原波波形各峰值点的出现时刻，即时程曲线由密变疏，这是由于结构局部已经达到屈服状态，结构刚度下降，频率也随之变化，从而影响了该结构响应加速度峰值出现的时刻。

(a) 不同地震波工况下结构总耗能

(b) 不同峰值加速度下滞回耗能时程曲线图8 滞回耗能Fig.8 Energy dissipation

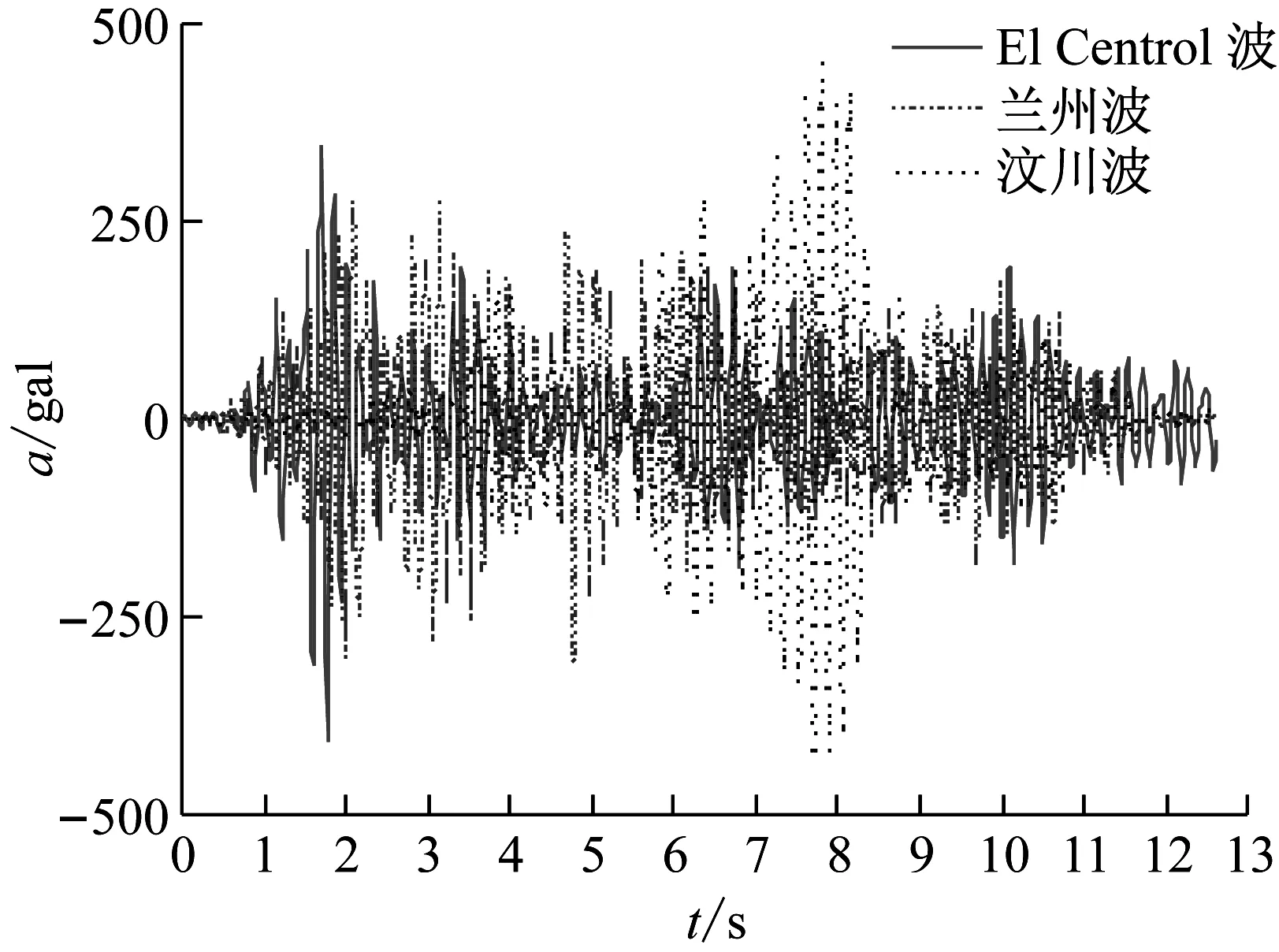
(a) 输入加速度峰值为200 gal

(b) 不同峰值输入加速度图9 加速度时程曲线Fig.9 Time history curves of acceleration

2.5 位移响应

结构加载点层高处在不同地震波作用下的位移时程曲线，如图10所示。分析可知，当输入加速度较小时，整个模型的位移反应很小，不同地震波作用下结构的位移反应与原波趋势大致相同，随着地震波输入加速度的增大，结构的位移响应同时增大。当施加峰值加速度为200 gal的地震波时，结构位移响应从大到小依次为汶川波3.795 mm、El Centro波3.041 mm、兰州波2.242 mm。其原因为汶川波频率与结构自振频率最为接近，而兰州人工波频率与本结构的频率差别相对较大。此外，模型结构最大位移响应出现时刻与原波输入加速度峰值时刻不完全一致。从图10还可知，620 gal时结构响应峰值时刻出现滞后现象，表明随着地震波加速度峰值增大，结构发生损伤导致刚度变化，使得位移响应有明显变化。

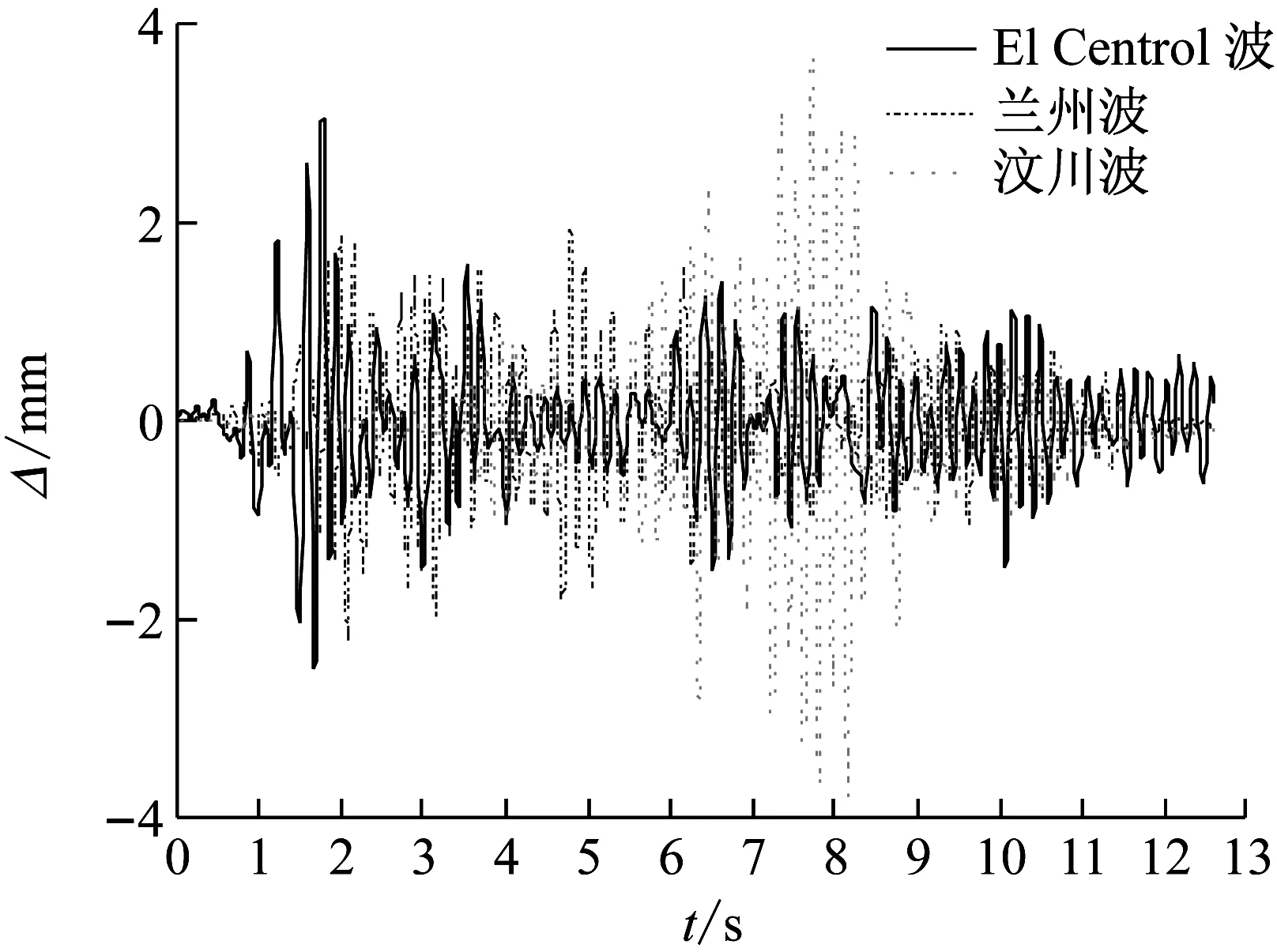
(a) 输入加速度峰值为200 gal

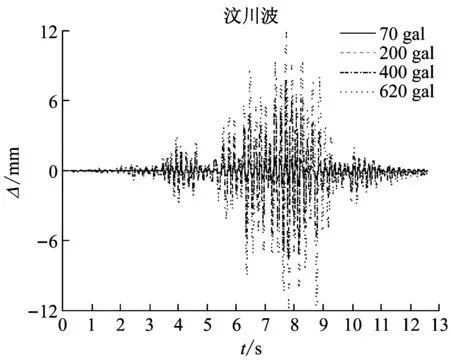
(b) 不同峰值输入加速度图10 位移时程曲线Fig.10 Time history curves of displacement

表5为在汶川波作用下，结构模型的层间位移角变化情况，可以看出，在8度多遇地震波作用下，结构最大层间位移角为1/1 903，满足“建筑抗震设计规范GB50011—2010”中关于多层钢结构弹性层间位移角限值[θe]=1/250的要求；在9度罕遇地震作用下，结构位移为11.962 mm，相应位移角1/203，可以满足规范中弹塑性层间位移角1/50的要求，说明本次试验仿古建筑钢框架结构具有良好的变形能力，能满足“小震不坏”和“大震不倒”的要求。

表5 层间位移角Tab.5 Inter-story drift

2.6 应变分析

异型节点处西侧拱G构件的应变情况，如图11所示。从图11可知，构件应变随着加载地震波加速度峰值的增大而增大，在加速度峰值为620 gal地震波的作用下，G构件屈服。分析试验应变数据可得，加载结束时，梁端翼缘应变接近屈服，且始终大于钢管柱端应变，满足规范“强柱弱梁”的设计要求。

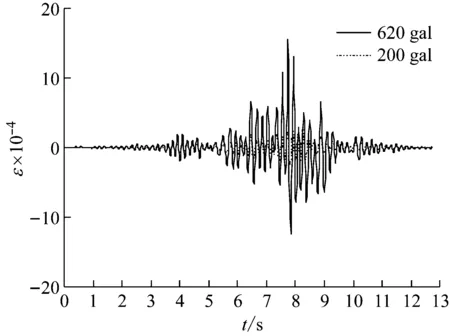
图11 拱G处应变Fig.11 Strain of G part

2.7 承载力分析

基于汶川波作用下的结构基底剪力-顶层位移曲线，将每级工况下正负方向的最大受力点连结可得到结构的骨架曲线，如图12所示。从图12可知，随着输入地震波峰值加速度的增大，结构位移响应增大，结构承载力不断增强，在9度罕遇地震烈度(620 gal)地震波的作用下，骨架曲线仍未进入下降段，此时结构最大层间位移角达到1/203，说明本试验的仿古建筑钢框架结构具有良好的承载力，且具有较高的安全储备。

图12 整体结构骨架曲线Fig.12 Skeleton curve of whole model

2.8 刚度分析

刚度退化问题是关系该种结构抗震性能及其抗震计算的重要内容[14]，对于加载地震波的拟动力试验，结构刚度取正负两个方向的平均刚度，即正负两个方向荷载绝对值最大值之和与相对应的两个方向位移绝对值之和的比值作为结构在不同工况下的结构刚度Ki，由式(5)计算。

(5)

式中：Pi、Δi分别为第i次加载时所达到的最大荷载及相应的位移。表6列出了在不同工况下结构的刚度，图13为模型结构的刚度退化曲线。加载初期由于作动器与试件之间存在少许间隙，故工况1测出的结构刚度相比于工况2略微偏低，K0取试验初始阶段工况2测得的刚度，即K0=6.129 kN/mm。

表6 结构刚度Tab.6 Stiffness of model

图13 模型刚度退化规律Fig.13 Deterioration trend of stiffness

分析图13和表6可知，模型刚度的衰减规律，在工况5 (200 gal兰州波) 之前，结构刚度基本没有变化，当作用200 gal、400 gal和620 gal汶川波时，由于试件出现累积损伤现象，使得整体结构刚度退化加快。当试验结束时，结构刚度仍达到初始刚度的81.9 %，这表明整体结构在9度罕遇地震作用后刚度仍然较大，满足设计要求，且安全储备较高。

3 静力推覆分析

为了了解本文所研究的仿古建筑钢框架结构在塑性阶段的反应，采用静力推覆分析的方法对该结构进行进一步分析，以期确定不同地震动强度下的结构目标位移及其承载能力。选用ABAQUS有限元软件建立试件三维模型进行Pushover理论分析。选用薄壳Shell单元对结构建模计算，钢材材性采用理想弹塑性强化模型，边界条件与试验保持一致。为了防止加载端出现应力集中，在加载部位设置刚性垫板。试件整体模型，如图14所示。

图14 结构有限元模型Fig.14 Finite element model

在静力推覆分析之前，采用模态分析得到该仿古建筑钢框架的频率及周期，与原型结构振动特性符合相似关系，如表7所示。

表7 结构自振特性Tab.7 Structural vibration characteristics

由于试验在9度罕遇烈度地震波加载后结束试验，采用有限元分析的方法模拟该仿古建筑钢框架结构屈服后至试件破坏的全过程。将有限元模型计算得到的P-Δ曲线与试验得到的结构整体骨架曲线对比可以发现，数值计算刚度略大于试验值，最大误差为9.61%，造成误差的原因主要是试验逐级施加地震波的过程中，结构损伤积累，刚度逐渐退化；总体上，有限元计算结果与试验结果趋势保持一致，吻合较好，数值计算得到的结构骨架曲线，如图15所示。

图15 骨架曲线计算结果Fig.15 Calculation of skeleton curve

试件的峰值荷载出现在168 kN处，此时位移为55.4 mm，层间位移角达到1/53，小于规范规定的弹塑性层间位移角1/50的限值，满足规范要求。

图16为试件屈服时异形节点处和斗D1处的应变分布情况，分析结构屈服过程可以发现，斗D1下部最先屈服，随后，柱Z2中节点处拱构件上部应变增大，进入塑性状态；梁端翼缘接近屈服，此时柱端仍处于弹性阶段，满足“强柱弱梁”的设计要求；此外，柱Z3、Z4与正厅大梁L1交汇的节点域处受力远大于屋架构件的受力情况，设计时应对这些节点处予以加强处理。

(a) 柱Z2中节点

(b) 斗D1图16 应变分布Fig.16 Strain distribution

当试件加载至位移角弹塑性限值1/50时，输出其应变云图，如图17所示。

图17 应变云图Fig.17 Strain contours

分析图17可知，结构最终破坏时，斗D2、D3，拱G，主梁L1东侧梁端及梁L2端部应力均较大，为该仿古建筑钢框架结构的薄弱部位。分析各构件的应力发展过程，在水平荷载作用下，斗D3、拱G构件率先屈服，起到第一级抗震防线的作用；随后梁L1及L2端部出现塑性铰，结构的损伤加重；当结构达到破坏荷载时，框架柱Z1-1、Z1-2、Z2的柱脚同时达到屈服应力，结构层间位移角已超过1/50，说明本文所设计的仿古建筑钢框架结构具有良好的变形能力。

4 结 论

(1) 在输入不高于8度罕遇地震波作用时，本试验的仿古建筑钢框架结构处于弹性阶段，可以满足“小震不坏、大震不倒”的设防要求；在输入9度罕遇地震波作用时，结构在异形节点处拱构件及正厅边柱斗构件发生屈服，此时结构层间位移角满足规范弹塑性位移角限值要求。

(2) 当输入峰值加速度为70 gal和200 gal的地震波时，结构累积滞回耗能较小；随着输入地震波峰值加速度的增大，模型损伤累积，耗能逐渐增大。本文研究的仿古建筑钢框架结构在8度罕遇地震作用下并无明显的塑性变形现象，说明整体结构具有较高的承载力及安全储备。

(3) 模型结构的加速度与位移响应均随着输入地震波峰值加速度的增加而增大。在相同加速度峰值的不同地震波作用下，结构的加速度时程曲线、位移时程曲线均有较大差别，说明输入地震波的频谱特性对结构的地震响应具有较大影响。

(4) 静力推覆分析结果表明，本文研究的仿古建筑钢框架满足抗震设防的弹塑性层间位移角限值规定；构件屈服的顺序为斗拱—梁端—柱脚，满足“强柱弱梁，强节点弱构件”的抗震设防要求，具有良好的抗震性能，可以应用于高烈度地震区。

参 考 文 献

[1] 张风亮. 中国古建筑木结构加固及其性能研究[D]. 西安: 西安建筑科技大学, 2013.

[2] 田永复. 中国仿古建筑构造精解[M]. 北京: 化学工业出版社, 2012.

XUE Jianyang, WU Zhanjing, SUI Yan, et al. Experimental study on seismic performance of steel double-beams column exterior joints in antique style building[J]. Journal of Building Structures, 2015, 36 (3): 80-89.

[4] HUANG B，SHU G. Experimental study on seismic behavior of a two-bay two-story light steel frame under cyclic loading[J]. Earthquake Engineering & Engineering Vibration, 2006, 26(6): 114-119.

[5] LIGNOS D G，CHUNG Y，NAGAE T，et al. Numerical and experimental evaluation of seismic capacity of high-rise steel buildings subjected to long duration earthquakes[J]. Computers & Structures, 2011, 89(11/12): 959-967.

[6] 熊二刚, 张倩. 中心支撑钢框架结构基于性能的塑性抗震设计[J]. 振动与冲击, 2013, 32(19): 32-38.

XIONG Ergang, ZHANG Qian. Performance-based plastic design method for steel concentrically braced frames[J]. Journal of Vibration and Shock, 2013, 32(19): 32-38.

[7] 黄炜, 陈国新, 姚谦峰. 密肋复合墙体在拟动力试验下的抗震性能研究[J]. 振动与冲击, 2007, 26(3): 49-54.

HUANG Wei, CHEN Quoxin, YAO Qianfeng. Study on aseismic performance of a multi-ribbed composite wall under pseudo-dynamic test[J]. Journal of Vibration and Shock, 2007, 26(3): 49-54.

[8] 魏志粉. 仿古建筑圆钢管柱-箱形截面双梁节点抗震性能试验与理论研究[D]. 西安: 西安建筑科技大学, 2014.

[9] 漆成. 仿古建筑钢管柱-工字钢双梁节点抗震性能试验与有限元分析[D]. 西安: 西安建筑科技大学, 2014.

[10] 郑山锁. 动力试验模型在任意配重条件下与原型结构的相似关系[J]. 工业建筑, 2000, 30(3): 35-39.

ZHENG Shansuo. Analogical ratio between scale models with less ballast and their prototypes under shaking table test[J]. Industrial Construction, 2000, 30(3): 35-39.

[11] 薛建阳, 王刚, 刘辉, 等. 型钢再生混凝土框架抗震性能试验研究[J]. 西安建筑科技大学学报(自然科学版), 2014, 46(5): 629-634.

XUE Jianyang, WANG Gang, LIU Hui, et al. Experimental research on seismic behaviors of steel reinforced recycled concrete frame structure[J]. Journal of J Xi’an Univ of Arch & Tech(Natural Science Edition), 2014, 46(5): 629-634.

[12] 薛建阳, 梁炯丰, 彭修宁, 等. 大型火电厂钢结构主厂房框排架结构抗震性能试验研究[J]. 建筑结构学报, 2012, 33(8): 16-22.

XUE Jianyang, LIANG Jiongfeng, PENG Xiuning, et al. Experimental study on seismic behavior of steel frame-bent structures of large thermal power plant main buildings[J]. Journal of Building Structures, 2012, 33(8): 16-22.

[13] 张锡成. 地震作用下木结构古建筑的动力分析[D]. 西安: 西安建筑科技大学, 2013.

[14] 白国良, 康灵果, 李红星, 等. 大型火力发电厂SRC框架柱-RC分散剪力墙主厂房混合结构体系抗震性能试验研究[J]. 土木工程学报, 2011, 44(9): 20-26.

BAI Guoliang, KANG Lingguo, LI Hongxing, et al. Experimental study of the seismic performance of hybrid structure of SRC frame columns-RC disperse shear walls for large thermal power plants[J]. China Civil Engineering Journal, 2011, 44 (9): 20-26.