海上浮式集装箱起重机的小车位置跟踪和吊重消摆控制研究

孙友刚， 董达善， 强海燕， 滕媛媛(.上海海事大学 物流工程学院，上海 20306；2.同济大学 机械与能源工程学院，上海 200092)

随着全球经济的一体化，集装箱物流业取得了突飞猛进的发展。与此同时，港口拥堵和港口水浅限制下大型集装箱运输船无法进港泊船也成为亟待解决的问题[1-2]。相比扩建岸边港口规模，建设“海上移动式港口(Mobile Harbor)”已经成为最灵活、经济和环保的解决途径[3-4]。这一概念是将集装箱起重机安装在浮式基础平台上，即浮式集装箱起重机系统(Offshore Container Crane，OCC)，对锚泊在深海的大型集装箱运输船进行装卸作业，并将其运输到目标港口[5],如图1所示。

图1 浮式集装箱起重机在海上装卸作业Fig.1 The offshore container crane on the sea

由于受海上风浪和小车运行轨迹的影响，吊运的集装箱会产生复杂的非线性动力学响应。特别是吊重的残余摆角严重影响作业效率，甚至引发安全事故。事实上，即使在运输和建筑业广泛采用的陆地起重机上，小车定位或吊重消摆也是研究热点。起重机控制领域的研究者们关注快速，无残摆，高效消摆的解决方法。目前的研究成果分为开环控制和闭环控制两大类。以输入整形和最优控制技术[6-8]为代表的开环控制对系统数学模型的准确度具有很强的依耐性。而闭环控制方法，通常和智能控制相结合，如H-2/H-infinity Control[9]，模糊控制[10]，神经网络控制[11]，滑模控制[12]等。此外，船用起重机的动力学和控制策略也已经被研究，通常被分为回转旋臂式起重机[13-14]和集装箱起重机[15-16]。方勇纯等[17]建立了回转式船用起重机系统的动力学模型，通过仿真分析各参数对系统状态的影响。Henry等[18]提出了一种延迟反馈控制律来抑制旋臂式船用起重机的摆振。Ham等[19]研究了浮吊的多体动力学响应。Ngo等[20]基于Lyapunov法设计了滑模控制器来抑制集装箱起重机负载的摆角。Ismail等[21]构建了基于LQR的滑动平面来跟踪起重机目标轨迹。

浮式集装箱起重机的船体容易受到波浪的作用而在水平和竖直方向都偏离设定好的位置。国内外研究学者提出大量基于非线性控制理论的动力定位系统来防止船体水平方向偏离设定位置[22-23]。此外，波浪补偿系统被提出以消除船体竖直方向运动的影响[24]。然而，船体的横摇运动并没有得到足够的重视。但是对于集装箱装卸作业，船体的横摇运动对小车的跟踪定位和负载的摆振影响重大。

因此，针对海洋干扰环境，本文首先基于动力学分析推导了船体横摇和升沉运动下，OCC系统吊运负载的动力学方程，揭示船体横摇、升沉和小车耦合运动对负载动力学行为的影响规律。然后，构建一种双层流形面并设计新型的双层滑模控制器，来同时实现海浪干扰下小车的位置跟踪和负载的摆动控制。采用Lyapunov方法, 通过严格的数学分析证明系统状态在滑模面上的收敛性。接着，建立OCC系统的虚拟样机模型，其中包括考虑钢丝绳柔性的OCC多体动力学模型和设计的控制器。通过大量的仿真来证明本文提出的控制策略的。最后，通过实验平台来验证轨迹跟踪和摆角抑制的实际控制性能。

1 动力学建模与分析

1.1 数学理论建模

传统岸边集装箱起重机上小车的运动和吊重的摆动是共面的，通过控制小车的运行轨迹可以进行电子消摆。但是浮式集装箱起重机由于船体有纵摇运动，会产生侧向摆动，而此摆动和小车运动不共面，不能由传统的电子防摇方法来消除。这里，因为大型船体的纵摇较小，且小车在侧向不运动，可采用一套机械防摇的装置来消除侧向摆动[25-26]。海浪作用下，海上浮式集装箱起重机和集装箱运输船(母船)相对运动较为关键。但集装箱运输船的尺寸大型化，它的旋转机动性受海浪影响不明显，我们可以假定母船是静止的。又因为将浮式起重机系泊到母船上可以抑制前者的运动，因此本文只讨论船体的两个运动，升沉和横摇。

为了推导浮式集装箱起重机的数学方程，引入三个坐标系,如图2所示。O0X0Y0是参考坐标系(附着于静止的母船)，将从左舷指向右舷的方向规定为X0轴正方向。OsXsYs为固定在船体重心的随船移动坐标系；OtXtYt为随小车移动坐标系。M,m分别为小车和吊重质量；h为起重机门架高度;x为起重机小车在随船参考坐标系中的坐标位置;l为吊绳长度;θ为吊重在小车运行平面内的摆角;fx表示对小车施加的作用力;y为船体在参考坐标系中的升沉位移；φ为船体在波浪激励作用下运动产生的横摇角。所以船的运动状态向量定义为(y,φ)。在参考坐标系下，可推出小车的位移pM和吊重位移pm如下。

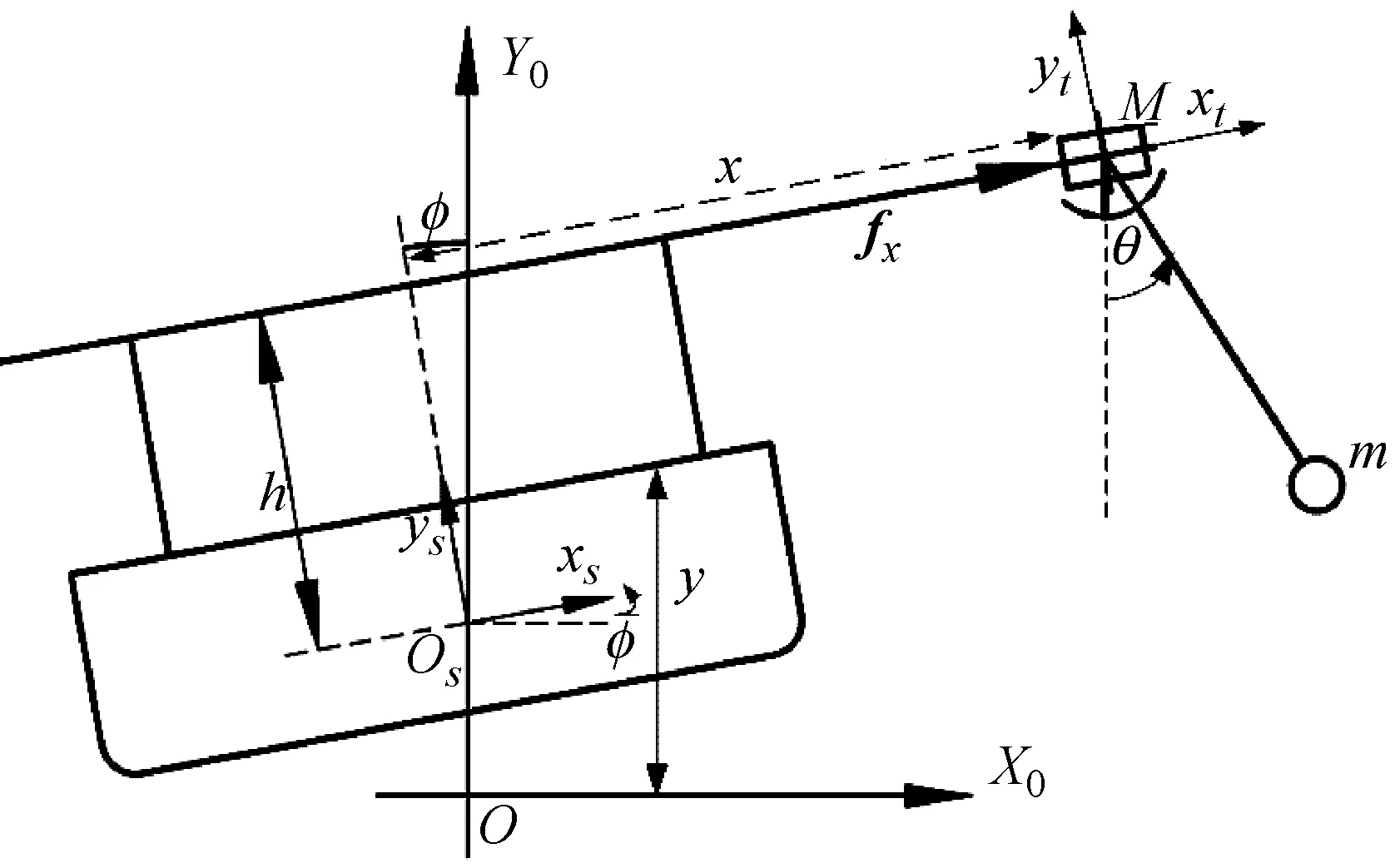
图2 引入坐标系：参考(母船)，船体，小车Fig.2 Ship-crane-payload system and reference frames

(1)

(2)

对式(1),式(2)关于时间微分，可得小车的速度vM和吊重的速度vm如下

(3)

(4)

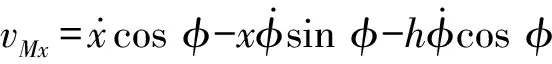
小车-吊重系统的动能和势能分别为

(5)

(6)

式中:g为重力加速度。这里不包含船的动能和势能，因为在本文研究中，船体运动(y,φ)被当作干扰。广义力取f=(fx,0)，广义坐标取q=(x,θ)，利用拉格朗日方程如下

(7)

可得小车和吊重的动力学方程如下

(8)

(9)

为了验证理论推导的动力学模型式(8),式(9)的正确性，搭建小型缩比物理样机，详见“4”节实验。选取动力学方程的参数和实验样机的参数保持一致，h=2.5 m，M=16 kg，m=4 kg，l=0.7 m，波浪引起的船体横摇取Sw(t)=0.01sin (0.8t) rad。对起重机模型施加一个驱动力fx=f0u(t)，取阶跃函数，每10 s一次，终值为20 N。用龙格库塔法对式(8)和式(9)进行数值求解，仿真50 s，采样时间0.01 s，将仿真结果和实验结果对比，如图3和图4所示。

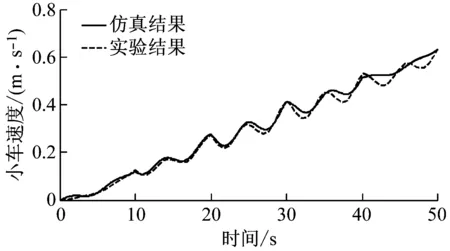
图3 小车速度响应曲线Fig.3 The trolley velocity of theory and experiment

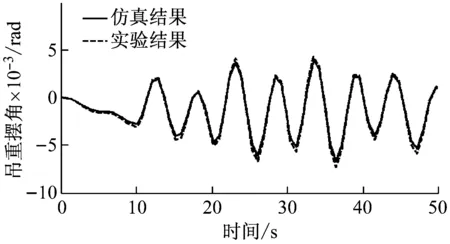
图4 吊重摆角响应曲线Fig.4 The payload sway angle of theory and experiment

结果表明:动力学方程的仿真结果和实验结果基本一致，证明了推导的动力学方程的有效性。

2 轨迹跟踪及消摆控制律设计

基于前一节推导出的OCC系统吊运过程的动力学方程，提出基于二阶滑模的轨迹跟踪和消摆控制器[27-30]。

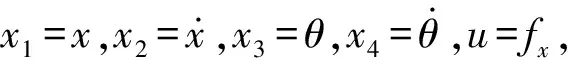
y(t)=[x1(t),x3(t)]T

(10)

式中：d1(t),d2(t)为外部干扰和系统参数摄动项；g1(X),g2(X),b1(X),b2(X)分别为如下的非线性函数

其中：

假设以下条件成立：存在非负常数g1M,g2M，使|g1(X)|≤g1M,|g2(X)|≤g2M；外界干扰和参数摄动有界，存在非负数d1M,d2M，使得|d1(t)|≤d1M,|d2(t)|≤d2M。

有别于全驱动系统，OCC系统受制于欠驱动与非线性特性，在构造流形面(滑模面)时须将多个不同的变量如小车运动与吊重摆角融合于一个流形面中。本文将系统状态分成两组来构造双层结构的流形面，分别为轨迹子系统流形面和摆动子系统流形面。

取小车目标轨迹位置为xd，小车实时轨迹位置为x。设目标摆角θd=0，实时摆角为θ，则误差向量为

(11)

第一层流形面可以定义为

(12)

式中：c1,c2为非负常数。

利用等效控制法分别求解各个子系统在流形面上的等效控制量ueq1和ueq2，即

(13)

(14)

OCC系统难以用一个控制量同时实现小车的轨迹跟踪和吊重的消摆，因此，采用构造双层流形面的方式，通过二级流形面S实现两组目标的同步联合控制。

S=αs1+βs2

(15)

式中：α为非负常数;β为随系统状态而选取的常数。

对于欠驱动系统，控制器不但要满足驱动部分稳定，还要满足欠驱动部分的自稳定性。因此，为了确保每个子系统都在自己的流行面上，系统的总控制律必须含有每一个子系统的控制式，设计总控制律如下

(16)

式中：usw为切换控制分量；η和k为非负常数。令

(17)

控制律的各项系数需要满足以下条件

(18)

(19)

η>|β||b2|K1

(20)

下面，基于Lyapunov法对所提出控制律的稳定性进行证明。

证明：对于第二层流形面S，选取Lyapunov能量函数为

(21)

对V(t)求导得

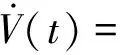
ST[α(c1x2+g1+b1u+d1)+

β(c2x4+g2+b2u+d2)]=

-ηαs1-ηβs2-(αb1+βb2)kS2≤0

(22)

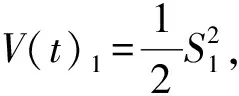
(23)

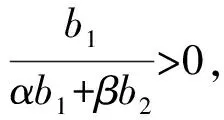
(24)

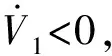
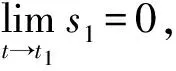
(25)

式中：T=max(t1,t2)∈R+

因此，第一层摆动子流形面s2同样是稳定的。

综上，所提出的控制器的系统状态都能在流形面S,s1和s2上同时渐近收敛至零，即不但满足了驱动部分稳定，还满足欠驱动部分的自稳定性。所以本文所设计的控制律可以同时实现小车的轨迹跟踪和吊重消摆。

3 虚拟样机仿真分析

3.1 多体动力学机械模型

因为制造全尺寸OCC并在真实海况下进行测试是十分困难的，本文采用虚拟样机技术进行仿真研究。

本节将钢丝绳当作柔性体，在ADAMS环境里建立OCC 系统的刚柔耦合多体动力学模型。浮式集装箱起重机的虚拟样机开发流程，如图5所示。

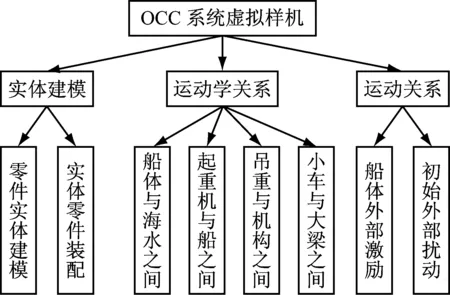
图5 OCC系统虚拟样机开发流程Fig.5 Development process of OCC’s virtual prototype

具体步骤如下:根据实际尺寸和形状用SOLIDWORKS建立OCC系统的3D模型. 然后将模型导入ADAMS环境中, 根据实际的材料属性, 质量, 转动惯量等相关参数来定义各个部件. 并且通过约束来连接每个部件. 如：小车和大梁通过平移副(Translational Joint)来连接，起重机门腿和船体之间用固定副(Fixed Joint)连接；钢丝绳和payload通过球铰(Spherical Joint)来连接. 卷扬机和小车之间通过旋转副(Revolute Joint)链接，钢丝绳和绳槽之间施加接触力(Contact Force)[31]。在船体中心添加波浪引起的横摇运动。开发的OCC系统多体动力学虚拟样机,如图6所示。

图6 OCC系统的多体动力学机械模型Fig.6 Multi-body dynamics mechanical model of OCC system

研究OCC吊运过程中，不加控制时的动力学响应。仿真时间选取50 s，小车的在x轴方向的跟随轨迹选取为x=step(t,0,0,18,2.7),设置起重机的相关参数和实验的物理样机一致。小车位移和吊重摆角的仿真和实验结果比较,分别如图7和图8所示。由图可知，仿真曲线与实验曲线有很好的一致性。

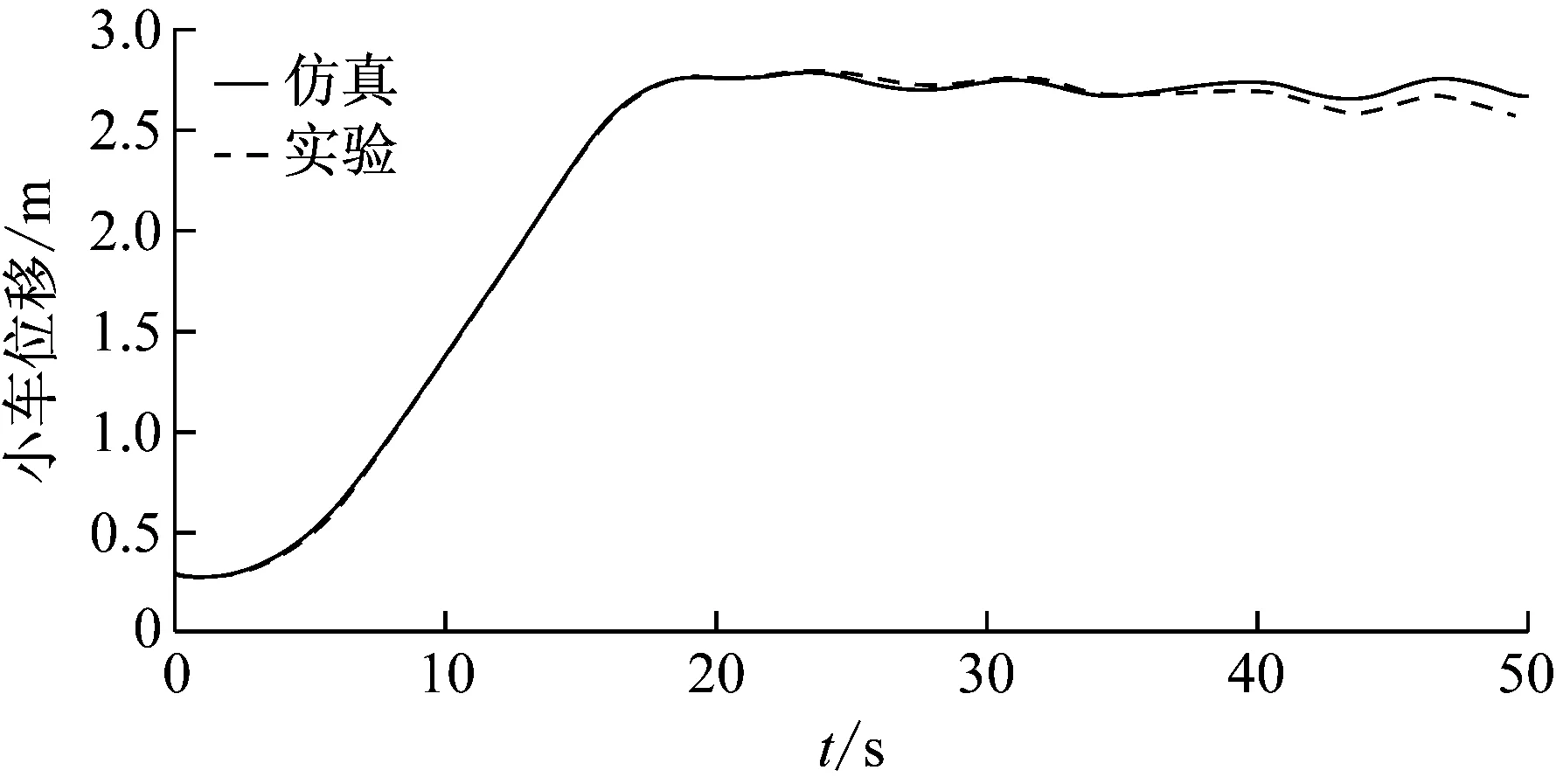
图7 小车位移的仿真和实验结果Fig.7 Simulation and experimental results of trolley position

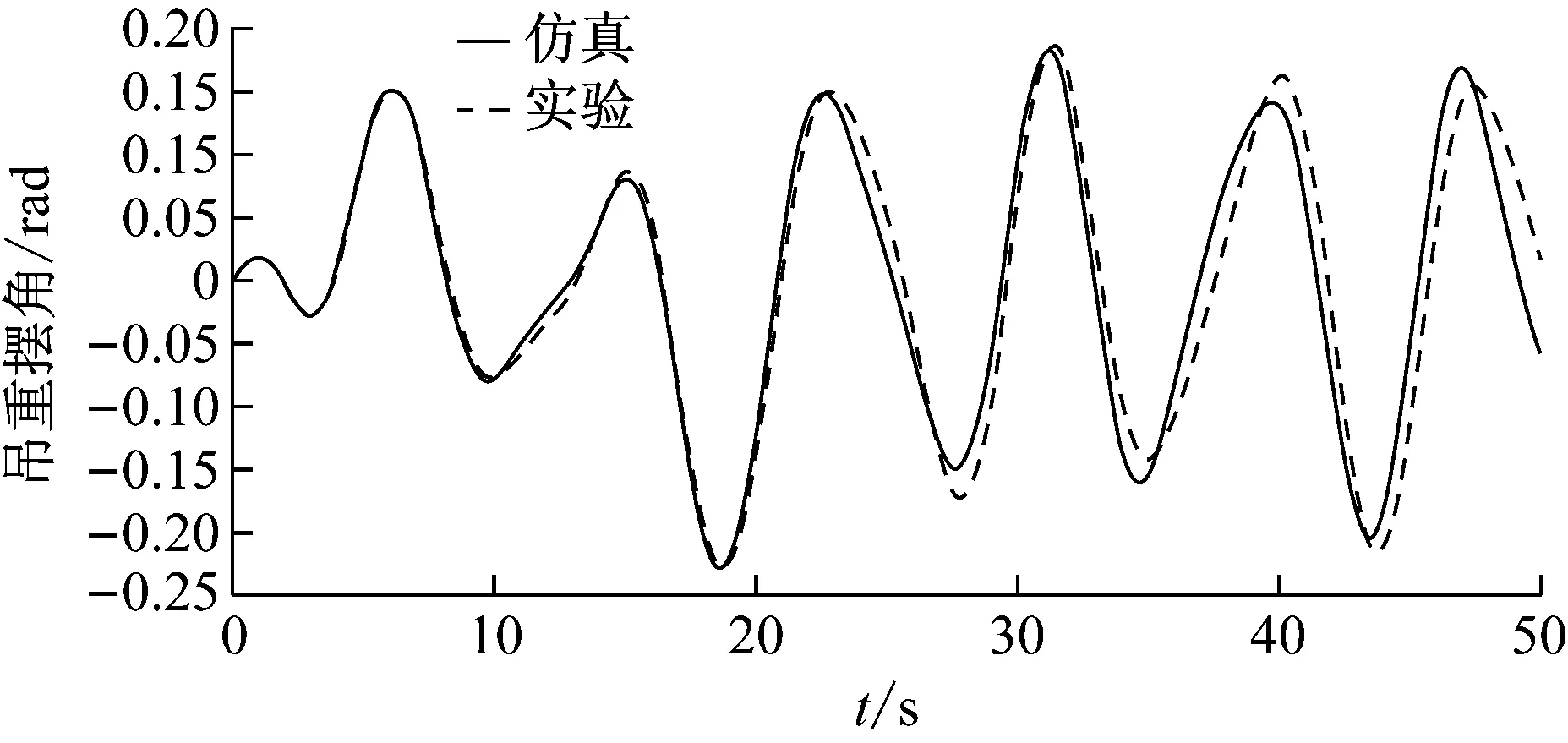
图8 吊重摆角的仿真和实验结果Fig.8 Simulation and experimental results of sway angle

因此，建立的机械多体动力学模型可以较真实的模拟OCC系统的动力学行为。此模型也能够被用于之后的OCC的控制系统的仿真，验证，测试和分析。

3.2 控制系统建模与联合仿真

根据“2”节设计的新型轨迹跟踪及消摆控制器，在MATLAB/SIMULINK中搭建控制模型。ADAMS软件中的ADAMS/Controls模块提供了MATLAB/SIMULINK控制接口,如图9所示。两个软件通过在系统间传递状态变量实现信息交流，在ADAMS中定义OCC机械系统的输入输出变量以及在MATLAB中定义控制系统的输入输出变量，以此在软件之间建立形成闭合回路，如图10所示。

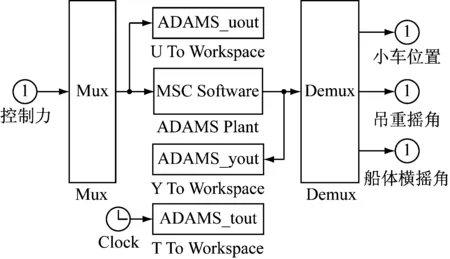
图9 ADAMS子模块和MATLAB/SIMULINK控制接口Fig.9 The ADAMS block in MATLAB/SIMULINK

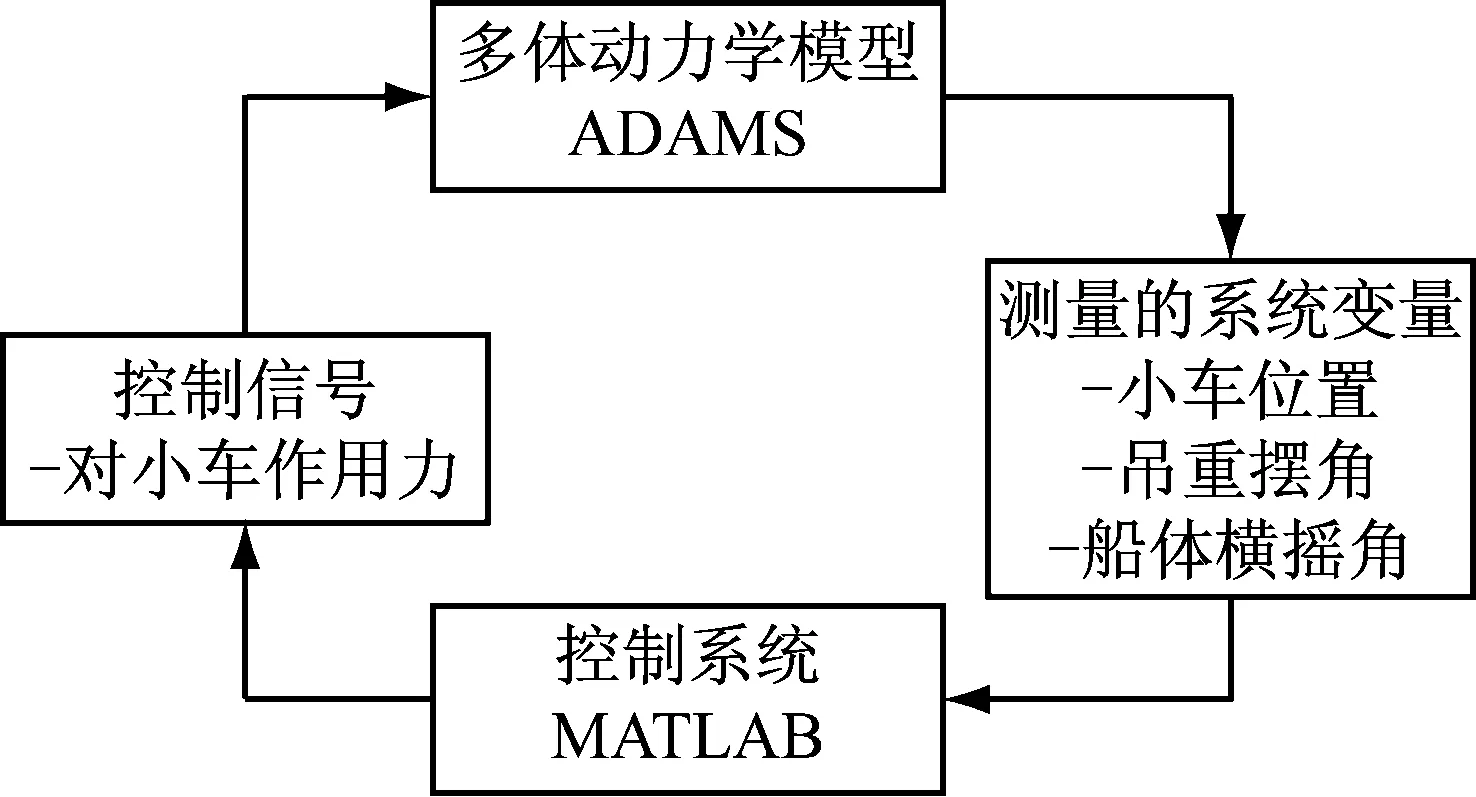
图10 ADAMS和SIMULINK的信号通信Fig.10 Communication of ADAMS and SIMULINK

将ADAMS机械动力学模型与基于MATLAB/Simulink的建立的控制器相结合，建立机电一体化的虚拟样机，如图11所示。

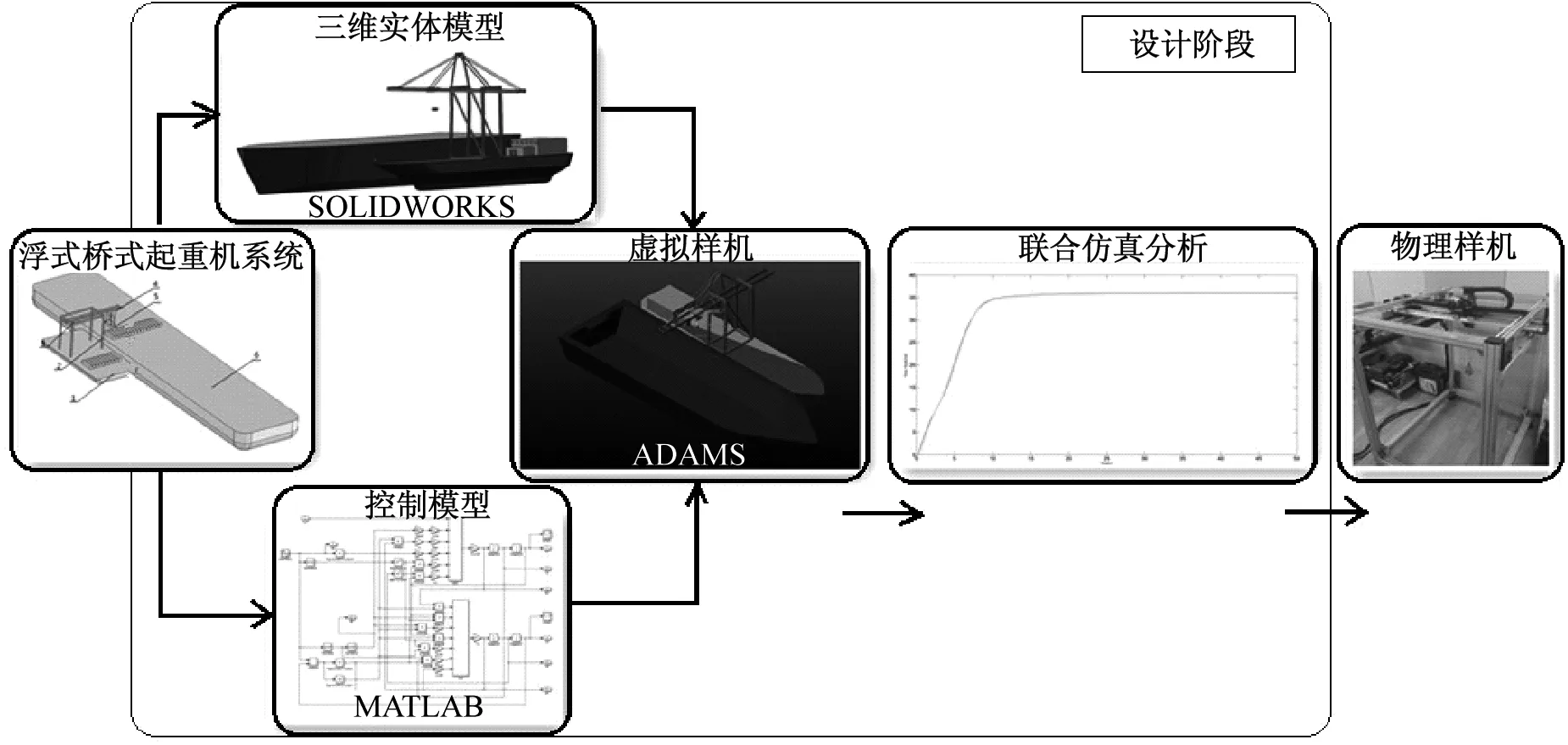
图11 机电一体化虚拟样机仿真模型Fig.11 The mechatronics virtual prototype

根据真实的OCC参数，设置仿真模型参数，h=48 m,M=2.0×104kg，m=2.0×104kg，l=15 m，小车目标轨迹位置xd=36 m。根据规则波下3、4级和5级海况[31-32],选取浮式平台横摇角分别为φ=0.007sin(1.25t) rad，φ=0.016 5sin(0.924t) rad和φ=0.028 6sin(0.714t) rad在建立的虚拟样机模型中，分别用传统的PID控制器和本文提出新型控制器(SOSM)进行控制, 并对比仿真结果。

(1)PID控制效果

这里选取传统的双PID控制器，用试错法选取控制效果最佳的一组控制器参数：位置控制的比例系数Pk=2 500，积分系数Pi=100,微分系数Pd=18 000,摆角控制的比例系数Pks=500,积分系数Pis=20,微分系数Pds=700。其中，PID试错法参数选取依据为：首先将Pi和Pd置零，将Pk值逐渐增大直到系统振荡，然后再逐渐增加Pd的值消除振荡，最后逐渐调整Pi的值消除静态误差。

在不同海况环境下，船舶横摇频率和最大幅度用froll和δroll表示。小车的水平位移曲线和吊重摆动曲线,如图12～图17所示。

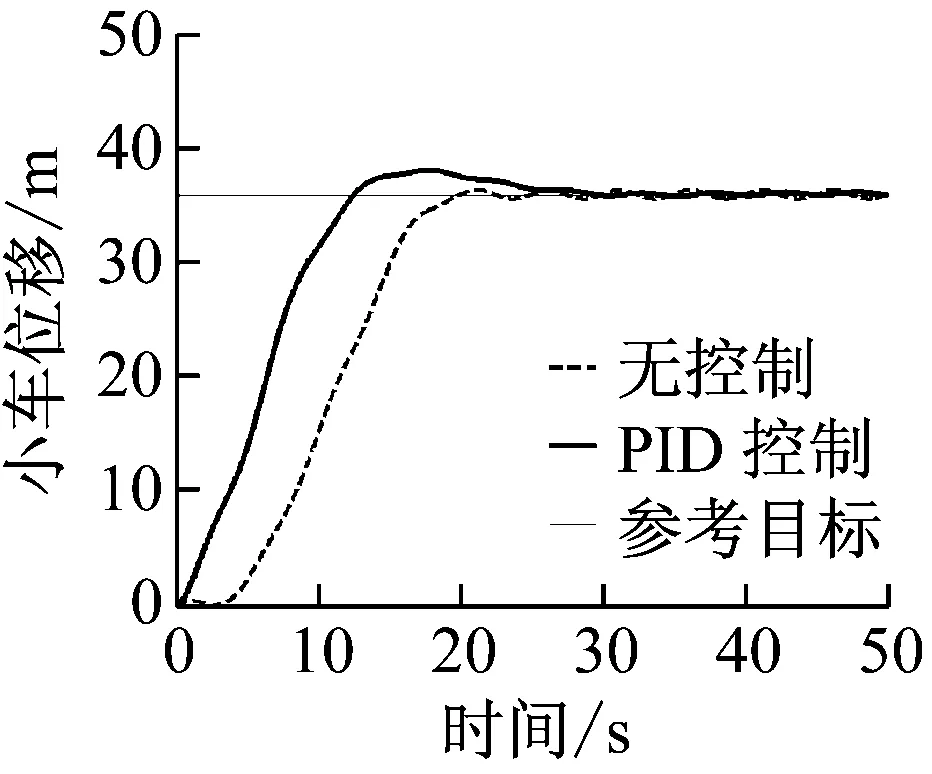
(a) 小车位移

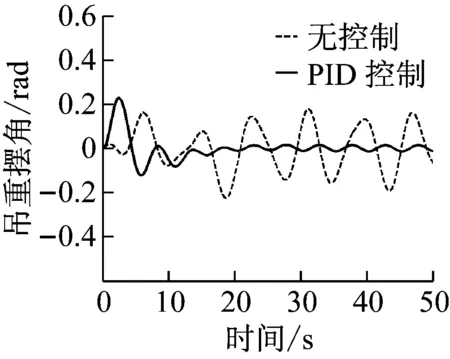
(b) 吊重摆角图12 PID控制器仿真结果(3级海况:froll=1.25,δroll=0.007)Fig.12 PID controller (sea state 3:froll=1.25,δroll=0.007)

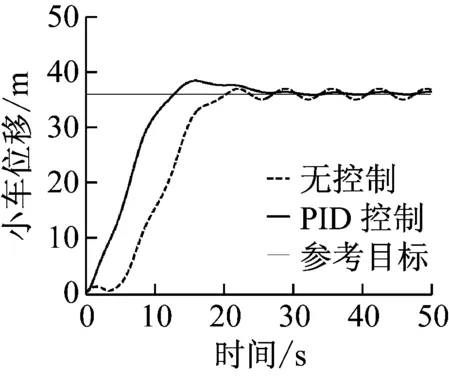
(a) 小车位移

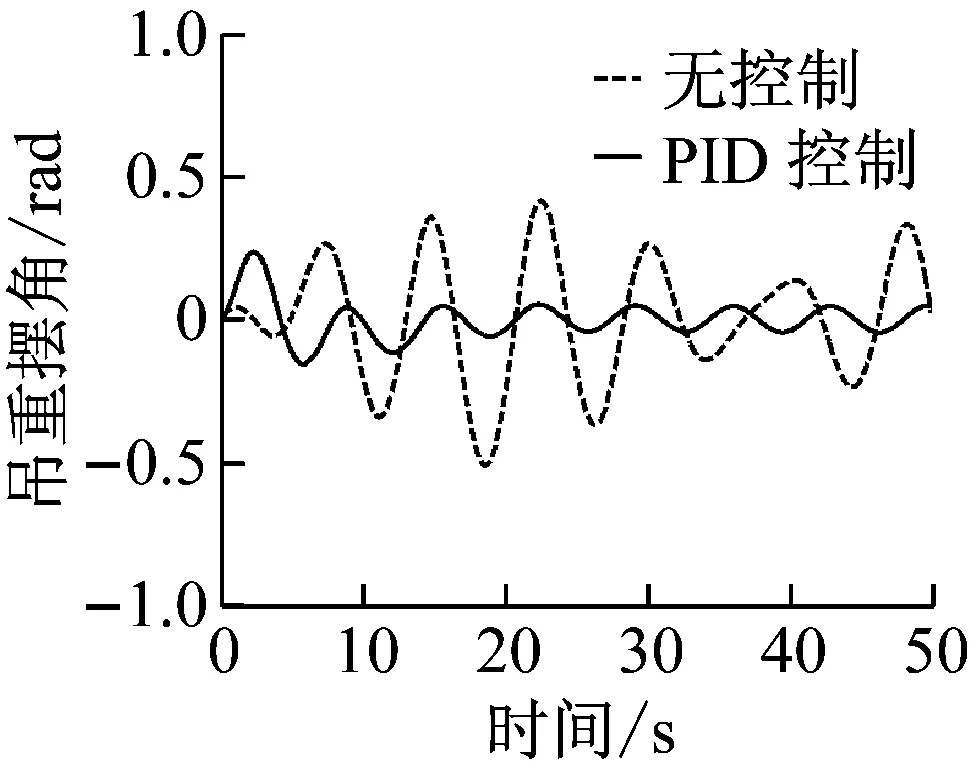
(b) 吊重摆角图13 PID控制器仿真结果(4级海况:froll=0.924,δroll=0.016 5)Fig.13 PID controller (sea state 4:froll=0.924,δroll=0.016 5)

(a) 小车位移

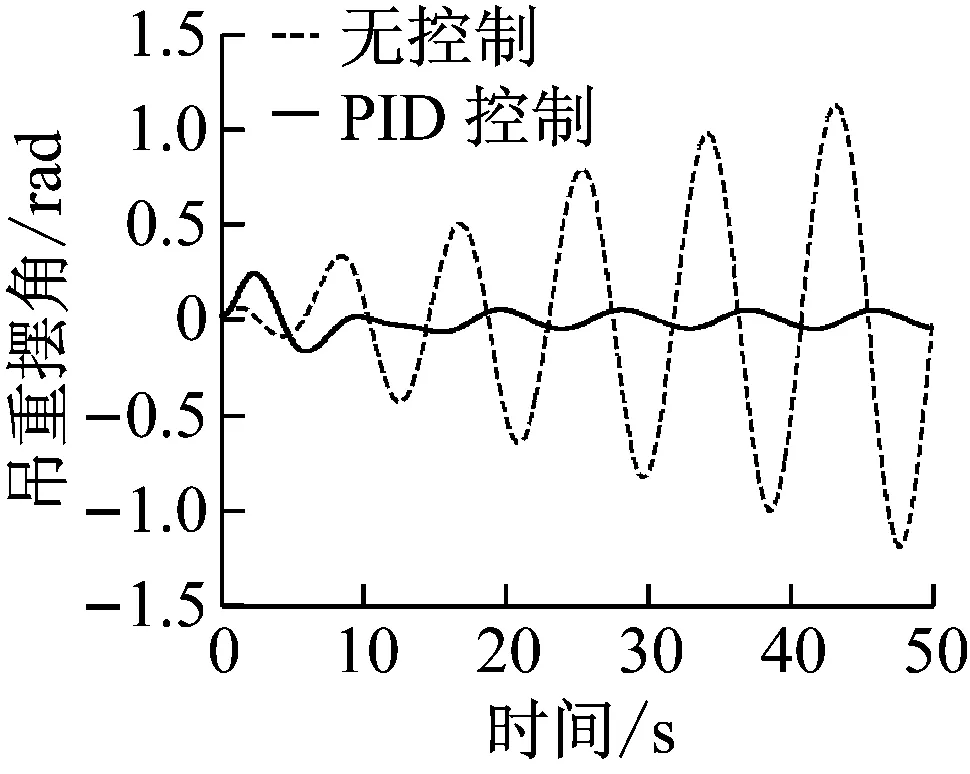
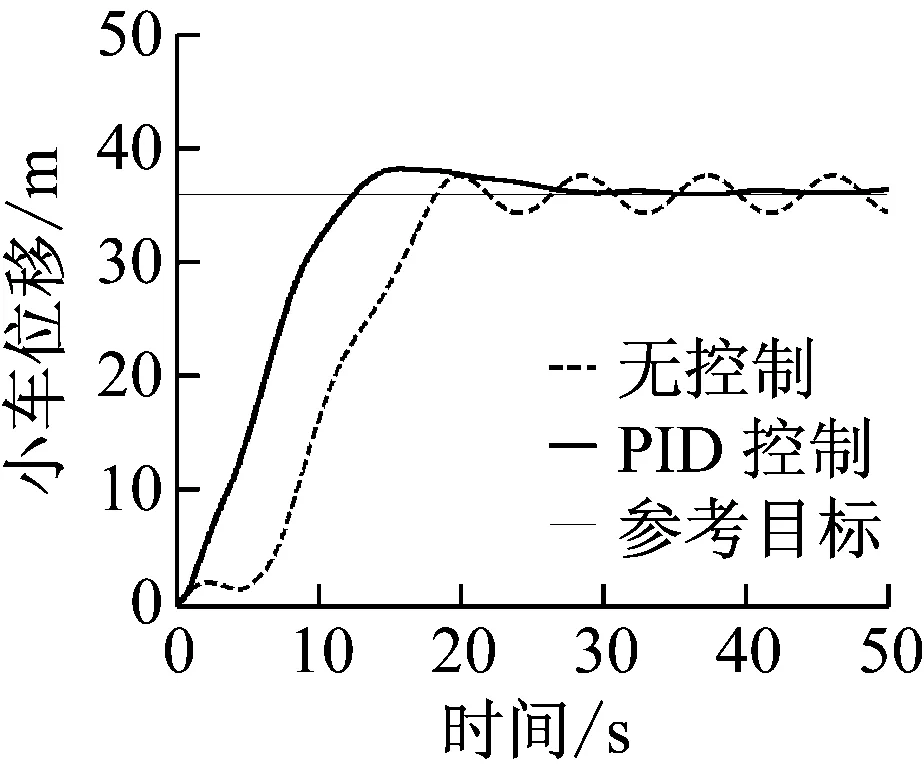
(b) 吊重摆角图14 PID控制器仿真结果(5级海况:froll=0.714,δroll=0.028 6)Fig.14 PID controller (sea state 5:froll=0.714,δroll=0.028 6)

(2)二阶滑模控制效果

在虚拟样机中应用本文提出的二阶滑模(SMC)轨迹跟踪及消摆控制律。采用LQR法[33]，其中LQR中的R=1，Q=CTC=diag(3 900,0,85,0)。得出SOSM控制器的最优参数:c1=0.8，c2=0.4，α=3.2，β=0.4，η=0.53，k=2。SOSM控制器作用下下，小车的水平位移曲线和吊重摆动曲线,如图15～图17所示。

(a) 小车位移

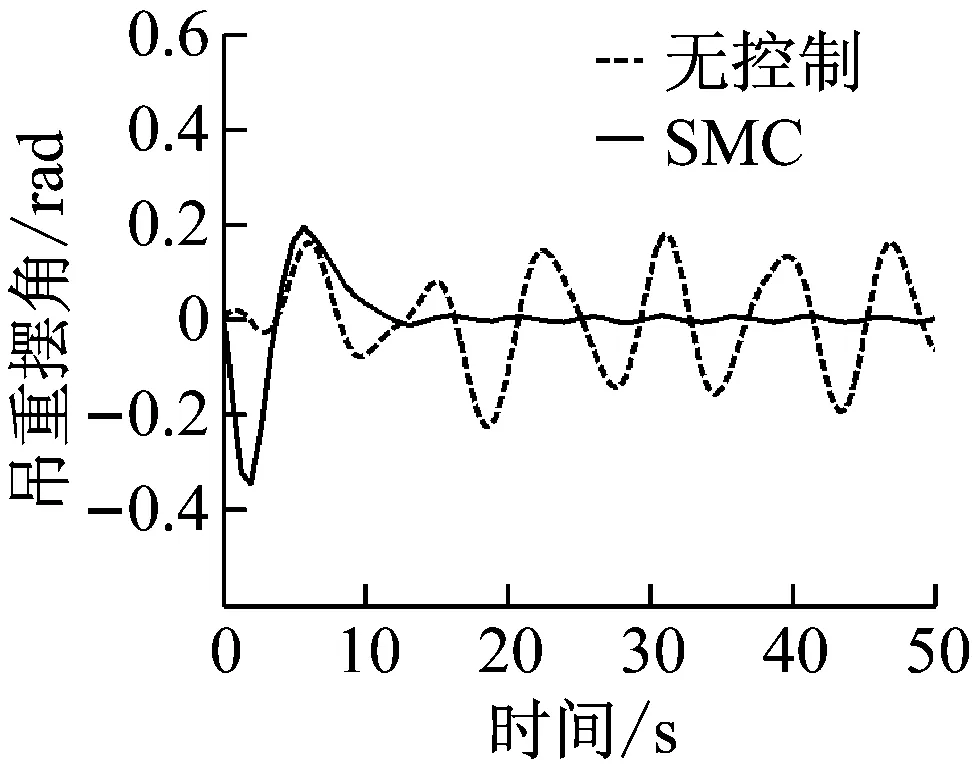
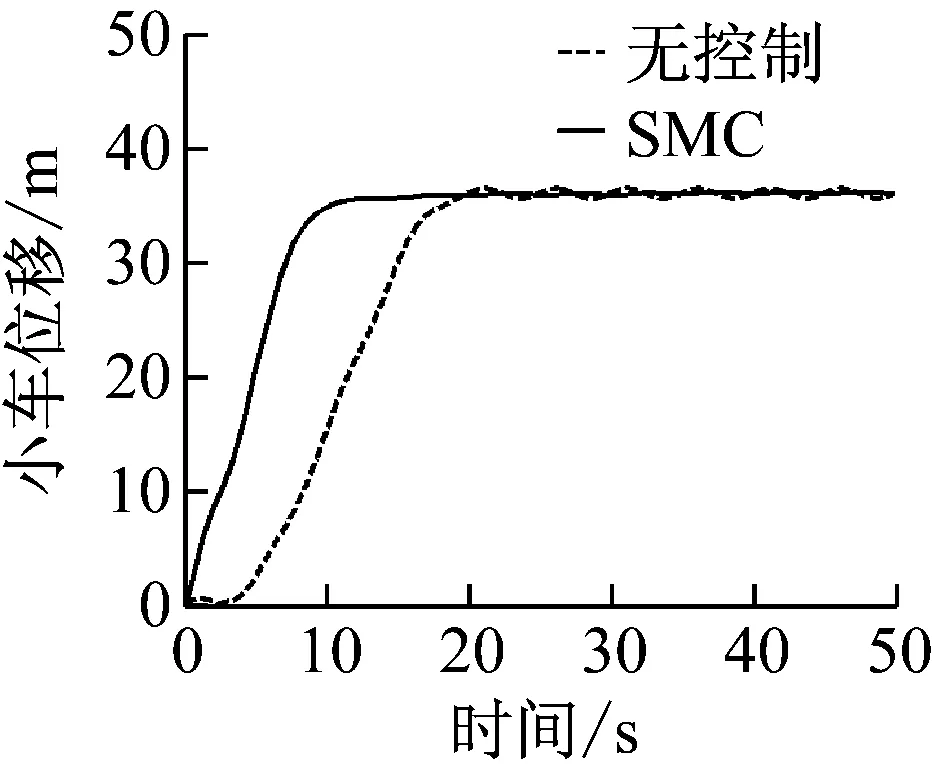
(b) 吊重摆角图15 SMC控制器仿真结果(3级海况:froll=1.25,δroll=0.007)Fig.15 SMC controller (sea state 3:froll=1.25,δroll=0.007)

(a) 小车位移

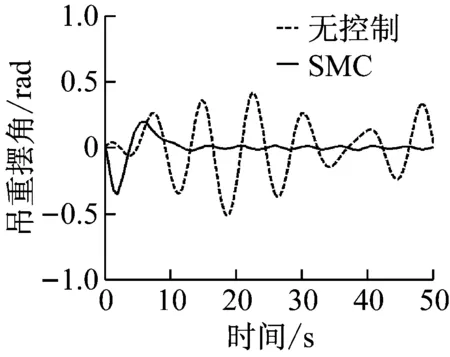
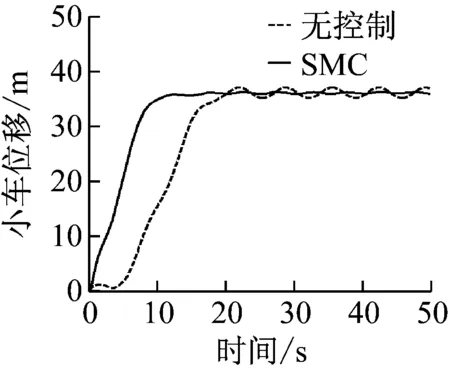
(b) 吊重摆角图16 SMC控制器仿真结果(4级海况:froll=0.924,δroll=0.016 5)Fig.16 SMC controller (sea state 4:froll=0.924,δroll=0.016 5)

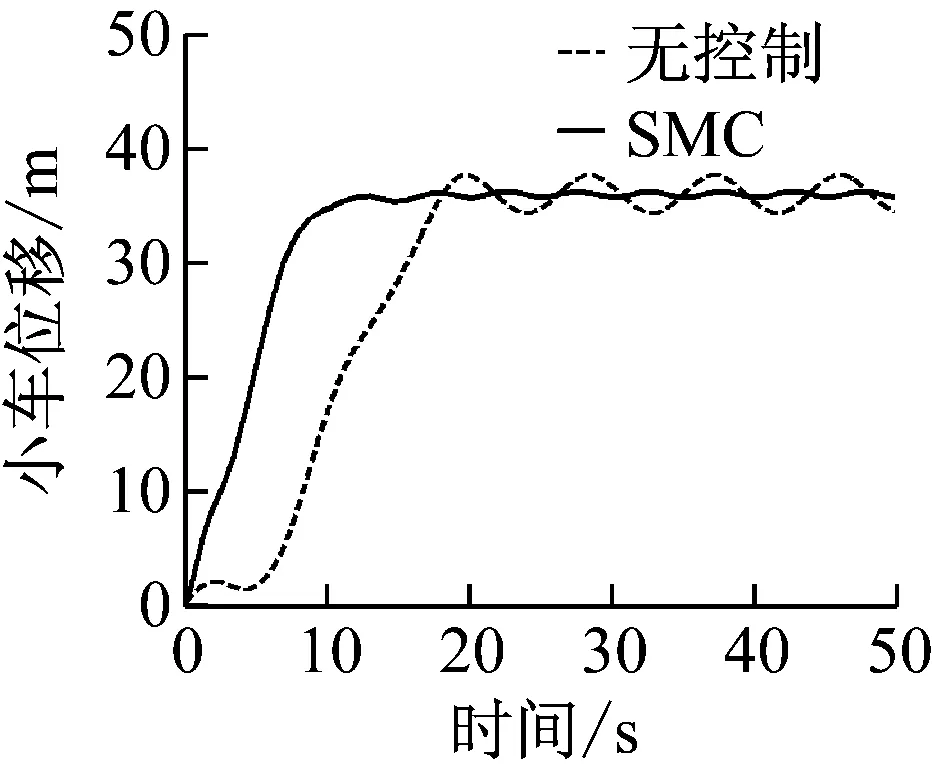
(a) 小车位移

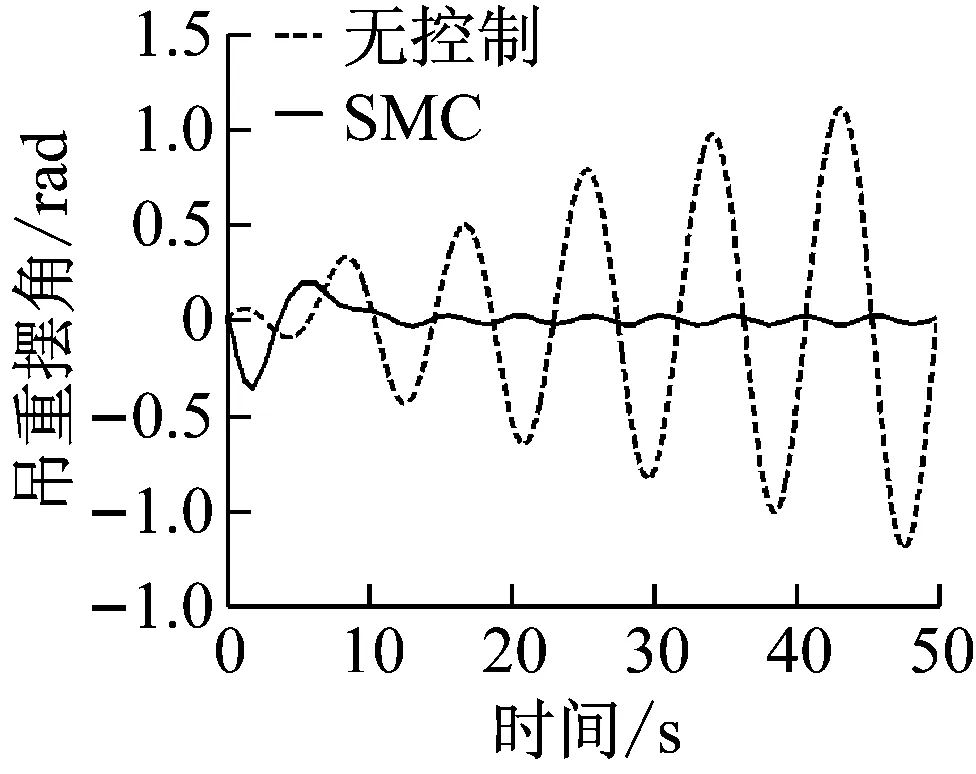
(b) 吊重摆角图17 SMC控制器仿真结果(5级海况:froll=0.714,δroll=0.028 6)Fig.17 SMC controller (sea state 5:froll=0.714,δroll=0.028 6)

OCC系统控制的目标包括跟踪小车位置和抑制吊重的摆动。小车运行需要快速并减小超调。具体控制目标为：稳定时间≤15 s，超调≤2%，稳态误差≤±0.05 m。吊重需要快速抑制摆角，具体控制目标为：稳定时间≤15 s，残余摆角≤±0.05 rad。

比较图12～图17所示的小车位置和吊重摆角响应. 用上述控制目标来分别评价不同控制方式下的控制器性能, 统计相关数据,如表1和2所示。

统计结果表明，传统PID控制下小车的超调量>2%，稳定时间>15 s，稳态误差>0.05 m，不满足小车跟踪目标位置的要求。而本文提出的SMC控制下超调量为0.74%～0.87%，稳定时间为 10.9～12.1 s，3级和4级海况下，稳态误差为0.02～0.04 m小于控制目标，5级海况下，因为船体横摇剧烈，稳态误差为0.11 m大于目标稳态误差。所以，本文提出的SOSM控制器，在3级和4级海况下能很好的满足控制目标要求，实现小车的快速精准轨迹跟踪。但仍无法在5级海况下的实现小车的精准定位。

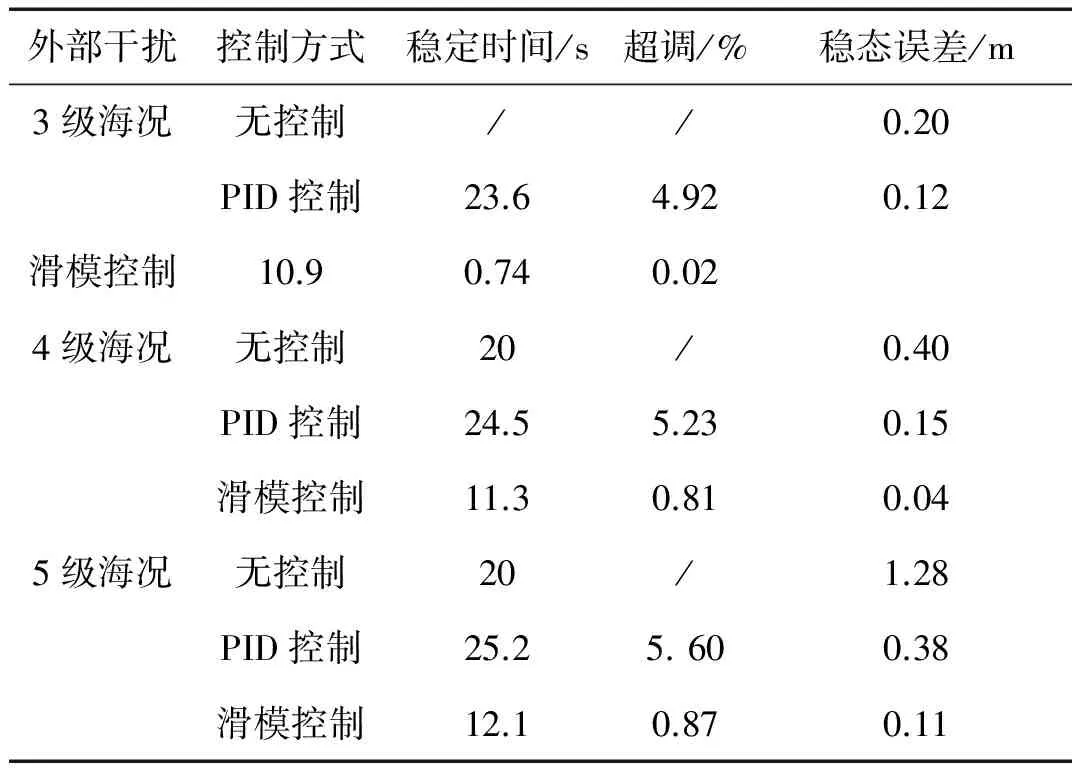
表1 小车位置响应对比Tab.1 Comparison of the trolley position response

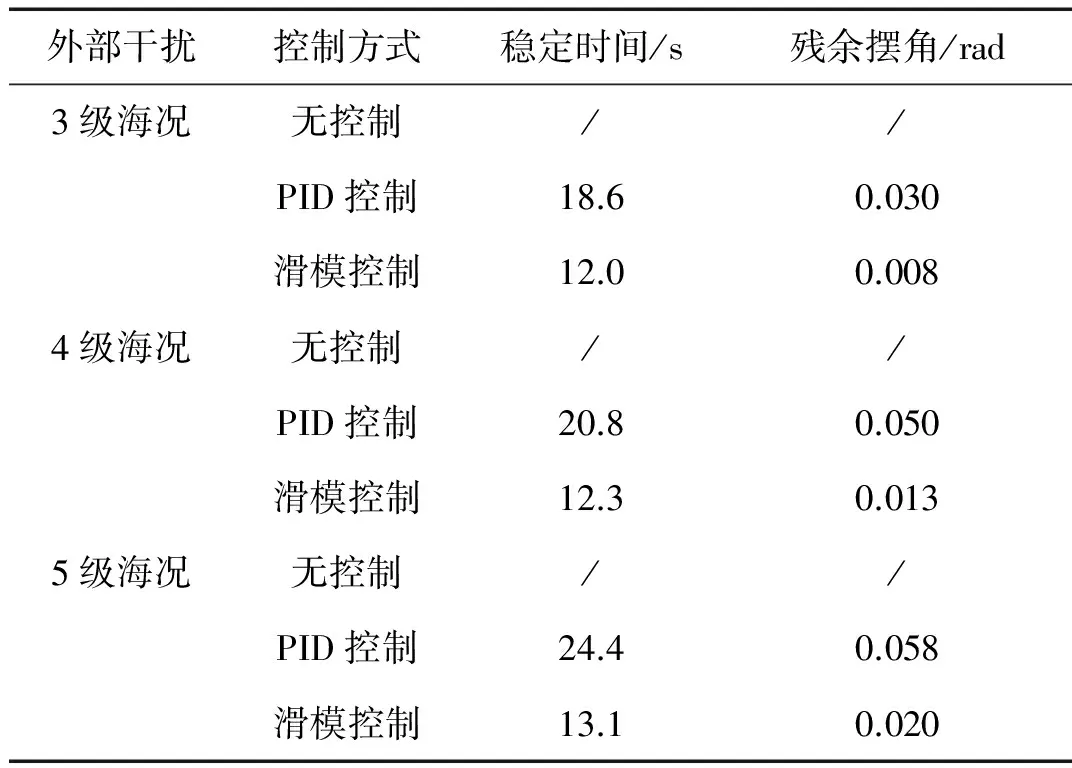
表2 吊重摆角响应对比Tab.2 Comparison of the payload sway angle response

对比控制器对吊重摆角的控制效果：传统PID控制器在稳定时间上要远大于目标时间，且残余摆角根据外界干扰变大而恶化，达不到对摆角的控制要求。而本文提出的SOSM控制器，不论外界干扰情况，滑模控制基本可以在13 s达到消摆目标，残余摆角≤0.02 rad。

综上所述，对于新型的OCC系统，因为海洋环境的复杂性，传统的PID控制方法已经不能满足控制要求，集装箱定位困难，容易引发碰撞事故。而本文提出的新型轨迹跟踪及消摆控制器鲁棒性强，在3级和4级海况干扰下，仍能够快速、准确地跟踪小车目标轨迹和较完美消除重物的摆动。

4 实 验

经过充分的仿真试验后，我们将搭建实验平台来进一步评估所提出的控制算法的性能表现。

因为搭建海浪干扰下的全尺寸浮式集装箱起重机系统是非常困难的，我们在实验室环境下建立如图18所示的试验平台。其中包括起重机主体，计算机/上位机，6自由度运动平台，摆角和位移传感器，伺服驱动系统和控制箱等，如图19所示。6自由度平台可以模拟船体的横摇运动。计算机/上位机采用MATLAB/Simulink RTWT(Real Time Windows Target)作为实时控制平台。DMC-1842型运动控制卡被用来规划上位机输出的信号，其功能框图,如图20所示。

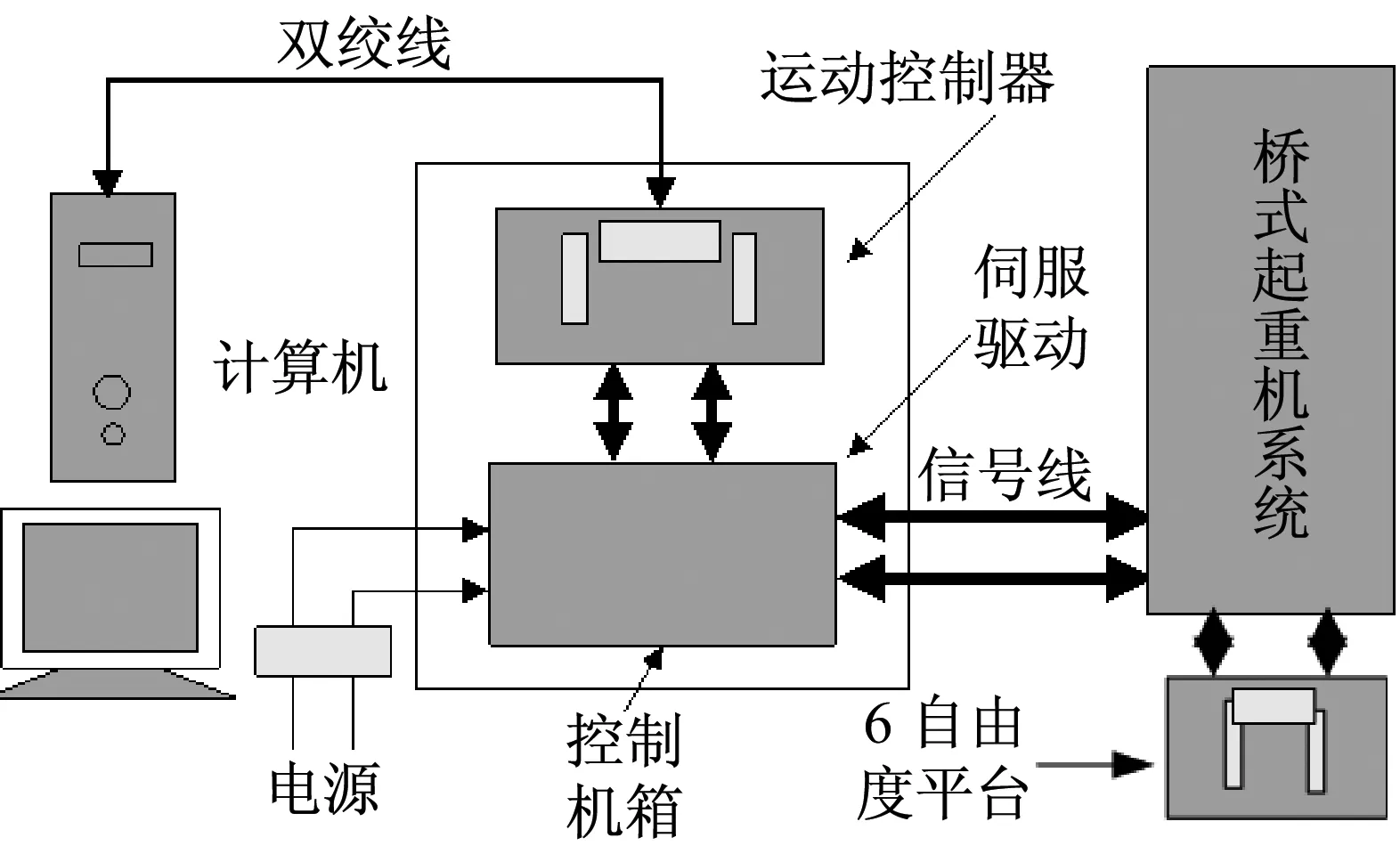
图18 实验平台结构图Fig.18 Structure of the experimental test bed

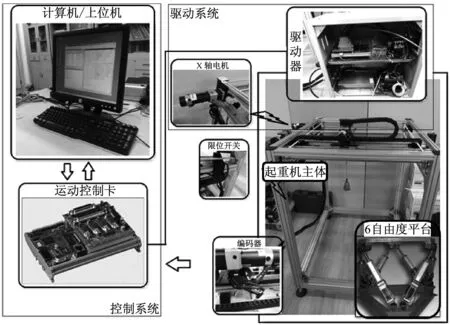
图19 实验系统Fig.19 Experimental system

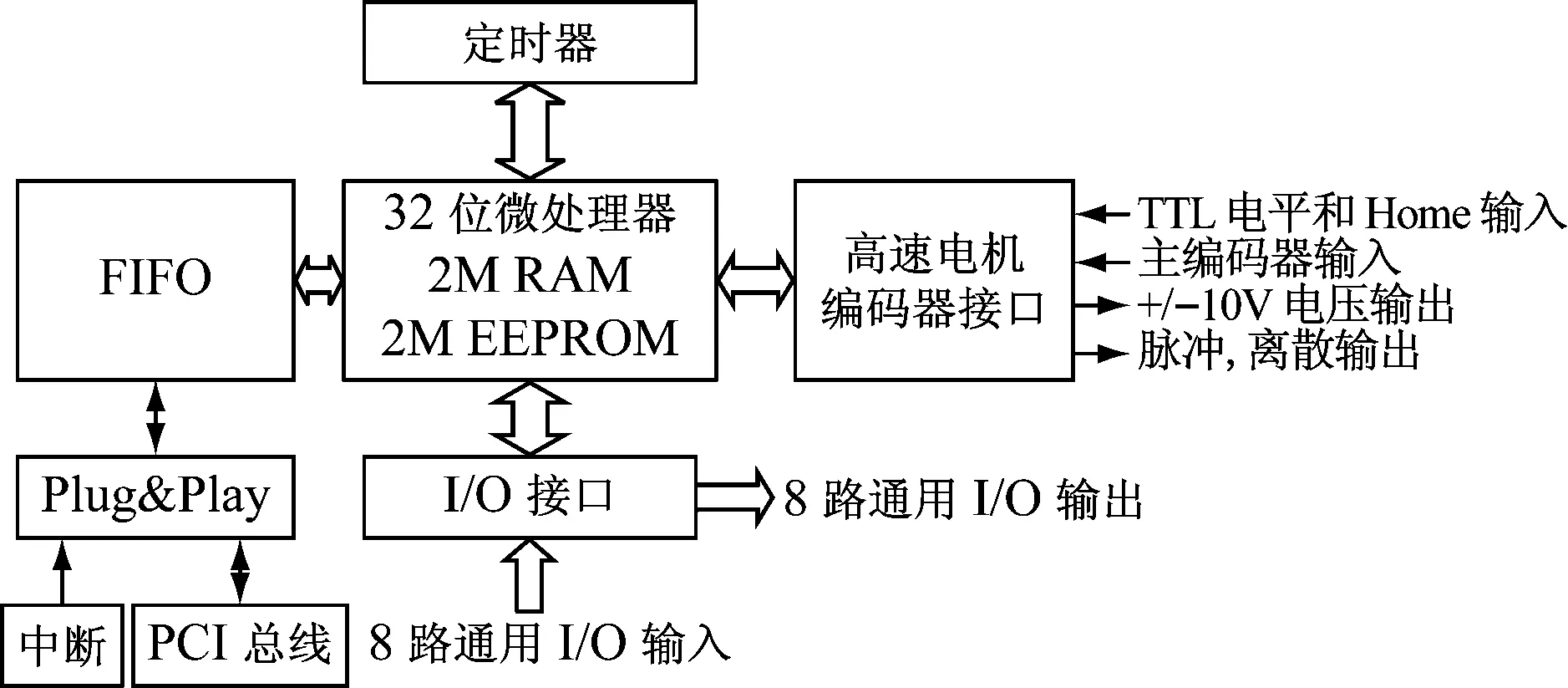
图20 运动控制卡功能框图Fig.20 Functional block diagram of motion control card

实验平台的系统参数为:h=2.5 m，M=16 kg，m=4 kg，l=0.7 m，小车目标跟踪位置xd=0.5 m。

因为数学模型和实验模型直接存在一些未建模动态，用基于数学模型的LQR整定本文提出的控制器参数并未达到最优。针对此实验平台，通过试错法仔细整定本文提出的控制器的相关参数和增益如下:

c1=1;c2=14;α=3.28;

β=1;k=22;η=1

为了全面研究所提出的定位消摆控制器的表现，分别进行两组实验来评估控制策略的位置跟踪表现和抑制吊重摆振的性能。

实验1无船体运动的情况

应用本文提出的跟踪和消摆控制算法的实验结果,如图21～图23所示。其中船体为静止的，即φ=0。可以看出在小车没有达到目标位置之前，吊重的摆角就在2 s内被明显消除了。这样就可以在吊重(集装箱)刚到达目标位置时候就没有残余摆角，直接可以进行对箱操作，大大增加了作业效率。

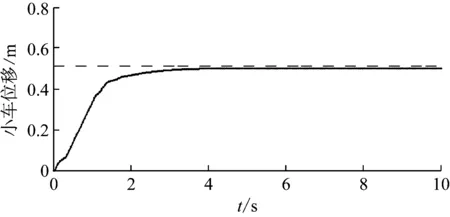
图21 实验1结果：小车位置Fig.21 Results of experiment 1: trolley’s position

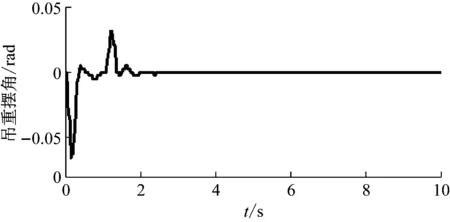
图22 实验1结果：吊重摆角Fig.22 Results of experiment 1: payload’s sway angle

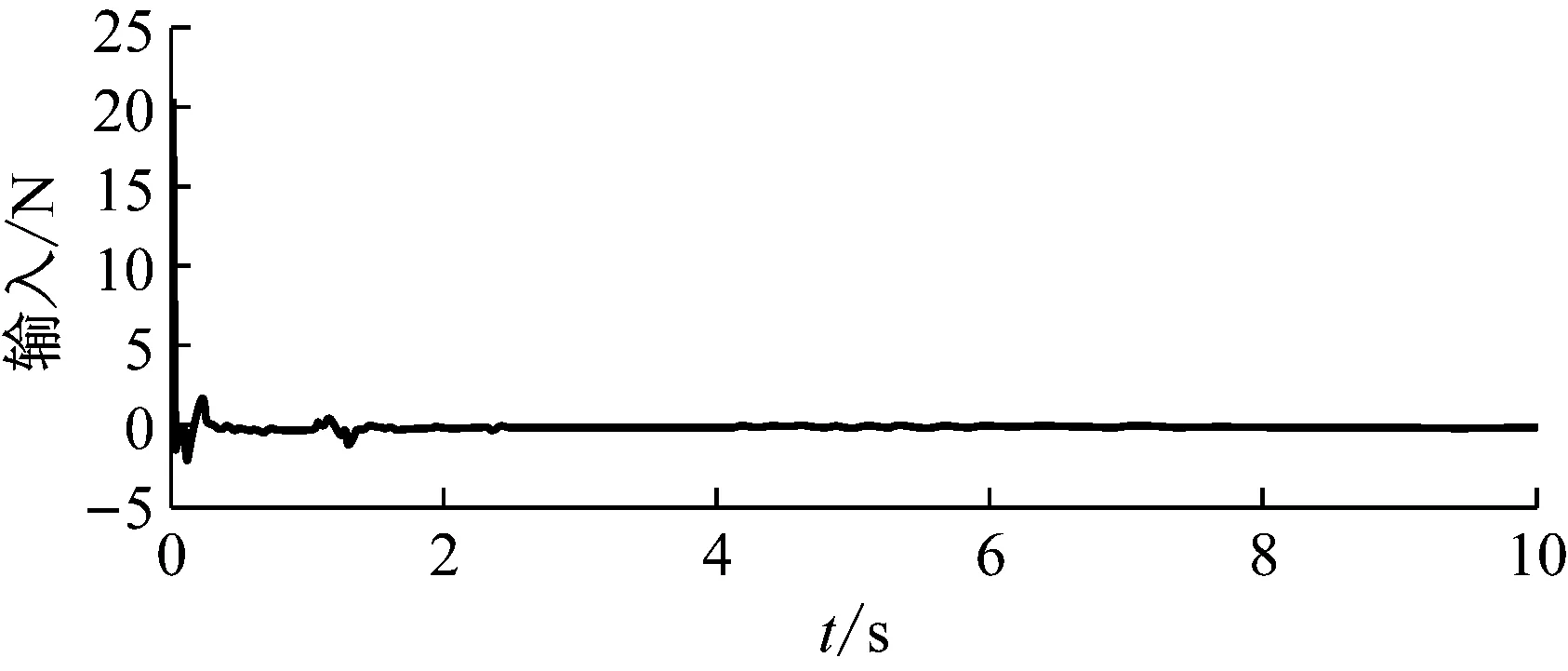
图23 实验1结果：控制量Fig.23 Results of experiment 1: control input

实验2船体横摇运动的情况

根据Marine Systems Simulator(MSS) toolbox(www.marinecontrol.org/),由波浪引起的船体的横摇角取值,如图24所示。

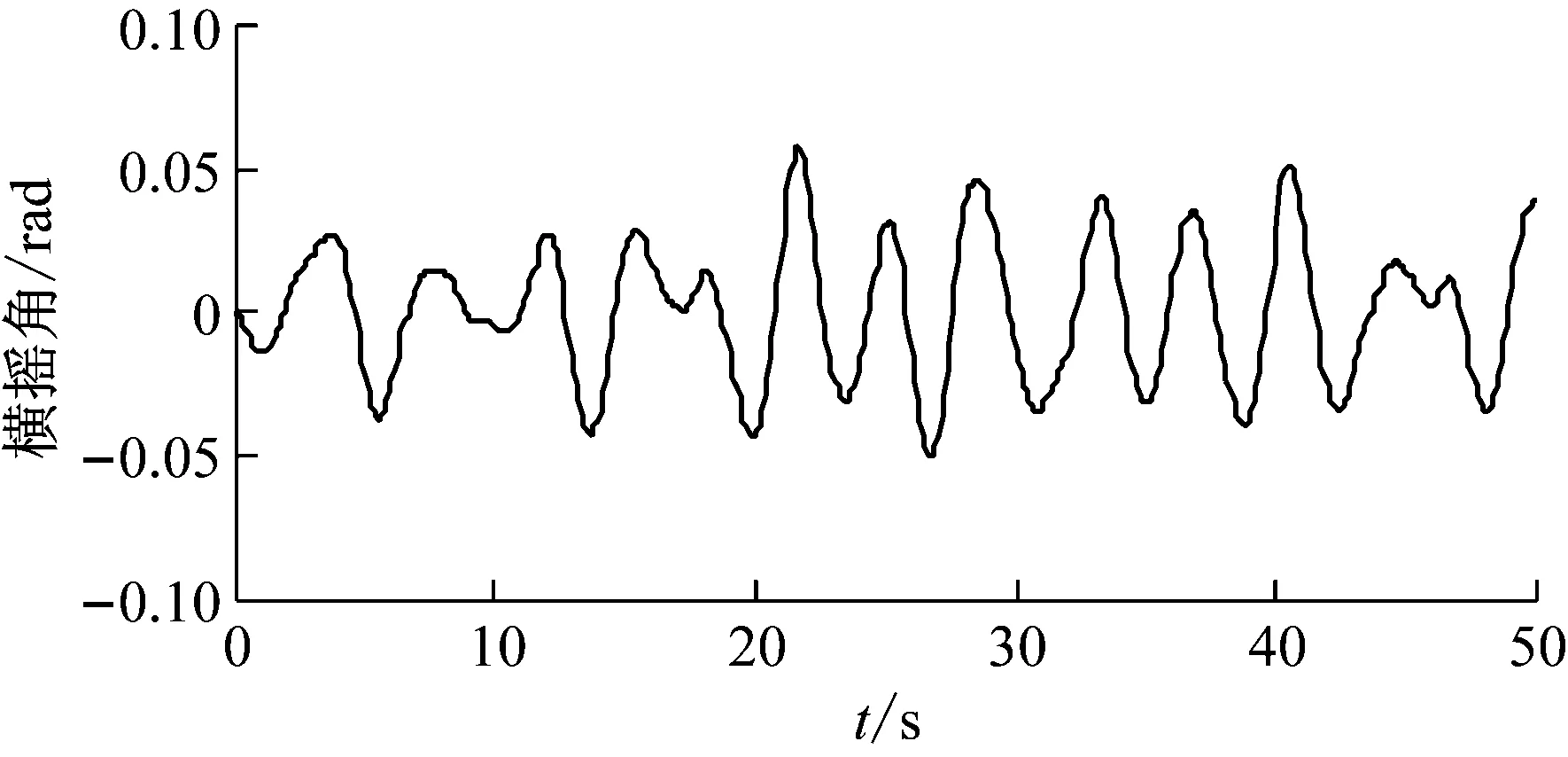
图24 船体横摇角Fig.24 The rolling angle

本文设计的控制策略在船体运动干扰下的控制表现,如图25～图27所示。图25表明在海浪干扰下小车能够快速的跟踪目标位置，且定位误差在可接受的区域[-0.02 m,0.02 m]内变化。从图26可知,在横摇干扰下，吊重能维持<0.02 rad的小残余摆角。显然，这是满足控制要求的。

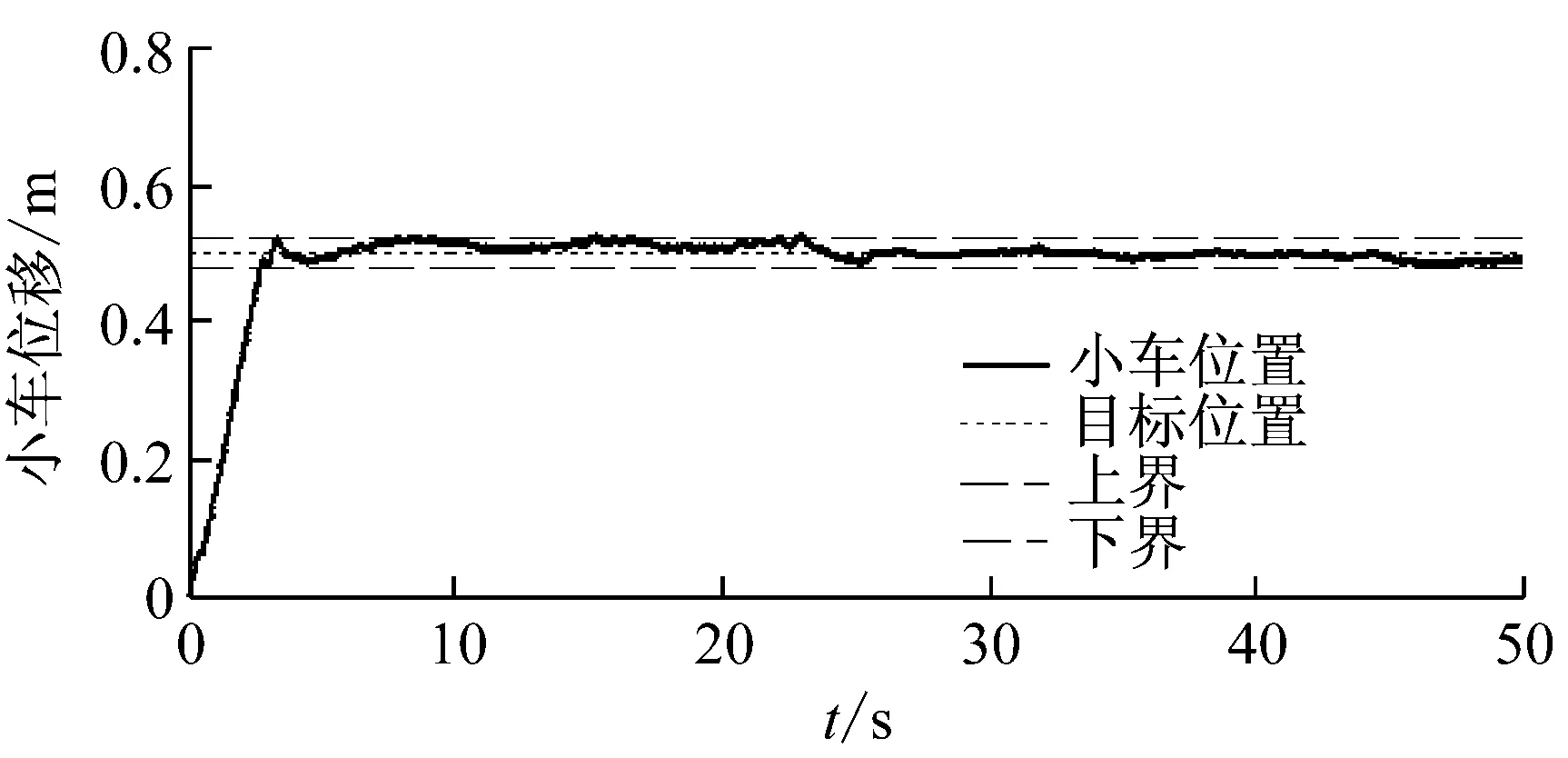
图25 实验2结果：小车位置Fig.25 Results of experiment 2: trolley’s position

图26 实验2结果：吊重摆角Fig.26 Results of experiment 2: payload’s sway angle

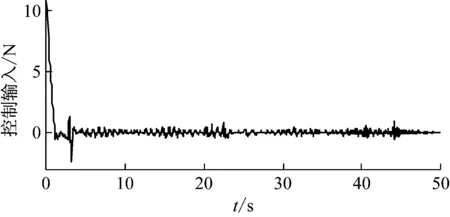
图27 实验2结果：控制量Fig.27 Results of experiment 2: control input

5 结 论

(1)本文的目的在于解决船体运动干扰下海上浮式集装箱起重机负载吊运过程的小车位置跟踪和负载摆振抑制问题。首先，利用Euler-Lagrange方程，全面的推导出OCC系统负载吊运的非线性数学模型。然后，不做任何线性化处理，基于非线性模型，设计二阶滑模控制策略来完成控制目标。接着，建立OCC系统的虚拟样机，并且做了大量的仿真来说明在3级和4级海况下能很好的抑制残余摆角和跟踪误差，但是在5级海况下并不能胜任。最后，通过搭建实验平台来验证本文所提出方法的实际控制性能。

(2)本文提出的控制策略在稍作修改后可用于其他类型的起重机(包括门式起重机，塔式起重机等)，并且可作为其他欠驱动系统抗干扰控制的有益参考。

(3)在未来的工作中, 将考虑在吊运过程中加入对系统参数改变(荷载质量、悬绳长度)的识别。如载荷载质量的在线辨识等，实现对其重力进行完全补偿，以获得更好的鲁棒性。

参 考 文 献

[1] 林天倚，卢春霞. 基于拥堵控制的轴辐式海运网络枢纽港选择模型[J]. 上海海事大学学报，2013, 34(4):59-66.

LIN Tianyi, LU Chunxia. Hub port selection model of hub-and-spoke shipping network considering congestion control[J]. Journal of Shanghai Maritime University, 2013, 34(4):59-66.

[2] 宋志鹏，江南莼. 船舶大型化趋势受制于港口[J]. 中国船检，2016(2): 52-56.

SONG Zhipeng, JIANG Nanchun. Large-scale trend is subject to the port of the ship[J]. China Ship Survey, 2016(2): 52-56.

[3] BAIRD A J, ROTHER D. Technical and economic evaluation of the floating container storage and transhipment terminal (fcstt)[J]. Transportation Research Part C, Emerging Technologies,2013,30:178-192.

[4] JONGHOE K, JAMES R M. Offshore port service concepts: classification and economic feasibility[J]. Flexible Services and Manufacturing Journal,2012, 24:214-245.

[5] JANG I G, KIM K S, KWAK B M. Conceptual and basic designs of the mobile harbor crane based on topology and shape optimization[J].Structural and Multidisciplinary Optimization,2014,50:505-215.

[6] 董明晓，脱建智，任意翔，等. 最优输入整形抑制变参数桥式起重机载荷摆动[J]. 振动与冲击，2009,28(10):207-236.

DONG Mingxiao, TUO Jianzhi, REN Yixiang, et al. Optimalinput-shaper to suppress payload oscillation of bridge cranes with varying parameters[J]. Journal of Vibration and Shock, 2009,28(10):207-236.

[7] TERASHIMA K, SHEN Y, YANO K. Modeling and optimal control of a rotary crane using the straight transfer transformation method[J]. Control Engineering Practice,2007, 15(9):1179-1192.

[8] 欧阳慧珉，张广明，王德明，等. 基于S型曲线轨道的桥式起重机最优控制[J]. 振动与冲击，2014,33(23):140-144.

OUYANG Huimin, ZHANG Guangming, WANG Deming, et al. Optimal control for overhead cranes based on an S-shaped curve trajectory[J]. Journal of Vibration and Shock, 2014, 33(23):140-144.

[9] HILHORST G, PIPELEERS G, MICHIELS W. Reduced-order H-2/H-infinity control of discre-time LPV systems with experimental validation on an overhead crane test setup[C]∥ Proceedings of the 2015 American Control Conference. Chicago, IL: IEEE, 2015:125-130.

[10] CHANG C Y. Adaptive fuzzy controller of the overhead cranes with nonlinear disturbance[J]. IEEE Transactions on Industrial Informatics, 2007, 3(2):164-172.

[11] SAEIDI H, NARAGHI M, RAIE A A. A neural network self tuner based on input shapers behavior for anti sway system of gantry cranes[J]. Journal of Vibration and Control, 2013, 19(13): 1936-1949.

[12] ALMUTAIRI N B, ZRIBI M. Sliding mode control of a three-dimensional overhead crane[J]. Journal of Vibration and Control, 2009, 15(11): 1679-1730.

[13] CHIN C M, NAYFEH A H, MOOK D T. Dynamics and control of ship-mounted cranes[J]. Journal of Vibration and Control,2001, 7(6): 891-904.

[14] SKAARE B, EGELAND O. Parallel force/position crane control in marine operations[J]. IEEE Journal of Oceanic Engineering,2006, 131(3): 599-613.

[15] PARK H S, LE N T. Modeling and controlling the mobile harbour crane system with virtual prototyping technology[J]. International Journal of Control Automation and Systems,2012, 10(6):1204-1214.

[16] LE A T, LEE S G, LUONG C N. Robust controls for ship-mounted container cranes with viscoelastic foundation and flexible hoisting cable[J]. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering,2015, 229(7): 662-674.

[17] 王鹏程, 方勇纯, 相吉磊, 等. 回转旋臂式船用起重机的动力学分析与建模[J]. 机械工程学报, 2011, 20: 34-40.

WANG Pengcheng, FANG Yongchun, XIANG Jilei, et al. Dynamics analysis and modeling of ship-mounted boom crane[J]. Journal of Mechanical Engineering, 2011, 20: 34-40.

[18] HENRY R J, MASOUD Z N, NAYFEH A H, et al. Cargo pendulation reduction on ship-mounted cranes via boom-luff angle actuation[J]. Journal of Vibration and Control 2001,7(8): 1253-1264.

[19] HAM S H, ROH M I, LEE H, et al. Multibody dynamic analysis of a heavy load suspended by a floating crane with constraint-based wire rope[J]. Ocean Engineering, 2015,109: 145-160.

[20] NGO Q H, HONG K S. Sliding-mode antisway control of an offshore container crane[J]. IEEE-ASME Transactions on Mechatronics, 2012,17(2): 201-209.

[21] ISMAIL R M T R, THAT N D, HA Q P. Modelling and robust trajectory following for offshore container crane systems[J]. Automation in Construction, 2015,59: 179-187.

[22] DO K D, JIANG Z P, PAN J. Universal controllers for stabilization and tracking of underactuated ships[J]. Systems & Control Letters, 2002,47(4): 299-317.

[23] SERRANO M E, SCAGLIA G J E, GODOY S A. Trajectory tracking of underactuated surface vessels: a linear algebra approach[J]. IEEE Transactions on Control Systems Technology, 2014,22(3): 1103-1111.

[24] SUN Y G, LI W L, DONG S D, et al. Dynamics analysis and active control of a floating crane[J]. Technical Gazette,2015, 22(6): 1383-1391.

[25] HONG K S, NGO Q H. Crane and ship loading thereof: Korean Patent: 10-2009-0126946[P].2009.

[26] 王阳. 船用起重机防摇装置设计研究王阳[J]. 舰船科学技术,2013, 35(7):105-108.

WANG Yang. Research and design of an anti-swing mechanism for a shipborne crane[J]. Ship Science and Technology, 2013,35(7): 105-108.

[27] WANG W, YI J, ZHAO D, et al. Design of a stable sliding mode controller for a class of second order underactuated systems[C]∥Proc of IEEE Conference on Control Theory Application. Beijing, China, 2004: 683-690.

[28] QIAN D, YI J, ZHAO D. Multi layers sliding mode control for a class of under-actuated systems[C]∥Proc of IMACS Multi-conference on Computational Engineering in Systems Applications. Beijing, China, 2006: 530-535.

[29] QIAN D, YI J, ZHAO D, et al. Hierarchical sliding mode control for series double inverted pendulums system[C]∥Proc of the 2006 IEEE/RSJ, International Conference on Intelligent Robots and Systems. Beijing, China. 2006: 4977-4982.

[30] QIAN D, YI J, ZHAO D. Hierarchical sliding mode control to swing up a pendubot[C]∥Proc of the 2007 American Control Conference. New York, USA, 2007: 5254-5259.

[31] 董达善，孙友刚，刘龙，等. 基于虚拟样机技术的浮吊补给作业动态特性仿真研究[J]. 机械科学与技术，2015, 34(3): 393-397.

DONG Dashan, SUN Yougang, LIU Long, et al. Simulation study on dynamic characters of floating crane based on virtual prototype technology[J]. Mechanical Science and Technology for Aerospace Engineering, 2015, 34(3):393-397.

[32] 李积德.船舶耐波性[M].哈尔滨：哈尔滨工程大学出版社，2007.

[33] 张雷, 郭科. 最优控制方法及其应用[M]. 成都: 四川大学出版社, 2012.