考虑粗糙度的倾斜式双滚柱包络环面蜗杆传动弹流润滑分析
李金宽, 柳在鑫, 张 翠, 朱 焱(西华大学 机械工程学院, 成都 610039)
倾斜式双滚柱包络环面蜗杆传动[1-3]既能克服无侧隙双滚子包络环面蜗杆传动[4-5]中蜗杆齿根较薄、承载能力较弱等不足,也能解决滚锥包络环面蜗杆传动[6-7]中滚锥径向安装误差敏感、齿侧间隙无法调整、齿面磨损量无法补偿等问题。在机械传动机构件中,绝对光滑的接触表面是不存在的,如果接触(表面粗糙度值远小于润滑油膜厚度,将接触表面假设为光滑表面是可以的[8]。环面蜗杆传动常用的加工方法为磨削加工[9],而弹流润滑油膜的厚度常常只有几微米甚至<1 μm,这与蜗杆传动副的加工工艺形成的表面粗糙度处于同一数量级,因此在这种情况下接触表面的粗糙度就不能忽略。
国内外学者对于蜗杆传动的弹流润滑问题进行了相关研究。王进戈等根据Hooke润滑状态简图中各润滑状态区域内的油膜厚度公式对滚锥包络环面蜗杆传动进行了润滑状态的研究。Simon对一种新型的圆柱蜗杆传动进行了润滑特性研究,并分析了传动副的承载能力、功率损耗[10]。许立忠等[11]根据Dowson-Higginson 经验公式对超环面行星蜗杆传动的弹流润滑状态进行了研究。Sharif等[12]运用弹流润滑理论计入齿面弹性变形与润滑油的黏压效应,对渐开线蜗杆传动的润滑问题进行了研究。汪久根等[13]根据Chittenden等提出的油膜厚度公式分析了阿基米德蜗杆蜗杆传动的油膜厚度。邱昕洋等[14]利用杨沛然、温诗铸回归出的线接触热弹流润滑膜的最小膜厚公式对钢制平面蜗轮传动进行了弹流润滑分析。
以上研究是利用经验公式对蜗杆传动的弹流润滑问题进行的研究分析,而对粗糙齿面的蜗杆传动弹流润滑数值求解的研究较少。本文基于弹性流体动力润滑理论,考虑粗糙度的影响,根据牛顿流体润滑特性对倾斜式双滚柱包络环面蜗杆传动的线接触弹流润滑问题进行数值求解。
1 传动副啮合模型
倾斜式双滚柱包络环面蜗杆传动,如图1所示。图中γ为滚柱倾斜角。蜗轮由固定蜗轮和活动蜗轮组成,滚柱均匀分布在固定蜗轮和活动蜗轮的周向,滚柱轴线与蜗轮径向倾斜一定角度,且滚柱可绕自身轴线转动,蜗杆左右齿面分别由固定蜗轮和活动蜗轮上的滚柱包络而成。就单排滚柱而言,工作过程中存在侧隙,从而保证了传动的正常工作和良好的润滑,对整体而言,通过采用双排滚柱错位布置,消除了传动的回程误差,使传动平稳,提高了传动精度。

图1 蜗轮结构图Fig.1 Construction sketch of this worm drive
传动副在传动过程中为瞬时多齿啮合,接触线是复杂的空间曲线且每一个啮合齿对上仅有一条接触线。在啮合传动过程中,蜗杆齿面的曲率半径是时刻变化的,蜗轮齿面的曲率半径即为滚柱的半径Rk,为一定值,在传动过程中的综合曲率半径为
Rk=1/kσ
(1)
式中:kσ为诱导法曲率。
基于两纯滚动接触进行弹流润滑分析,设vw、vg分别为蜗轮和蜗杆在啮合点处的沿接触线法线方向的速度;根据文献[14]所提供方法求得vw、vg分别为
(2)
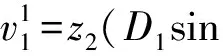
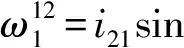
B1=(i21y2-z2cosφ2)
B2=(z2sinφ2-i21x2)
B3=x2cosφ2-y2sinφ2-A
x2=(a2+D2Rksinθ-D1u)
y2=(b2+D1Rksinθ+D2u)
z2=(c2+Rkcosθ)
D1=cosβcosγ-sinβsinγ
D2=-sinβcosγ-cosβsinγ
式中:(a2,b2,c2)为滚柱回转中心在蜗轮中的坐标值。β为两滚柱的齿周向夹角;u、θ均为滚柱的母面参数;ω0为滚柱的自转角速度ω0=(B2D2-B1D1)/Rk,i21为传动比,φ2为蜗轮转角。
则该传动副的卷吸速度为
vjx=(vw+vg)/2
(3)
每个齿对在啮合点处单位长度上的载荷为
(4)
式中:i=1,2,3,4;Ki为齿间载荷分配系数;L为接触线长度;αn为压力角;β为螺旋升角,T1为输入转矩;d1为蜗杆分度圆直径。
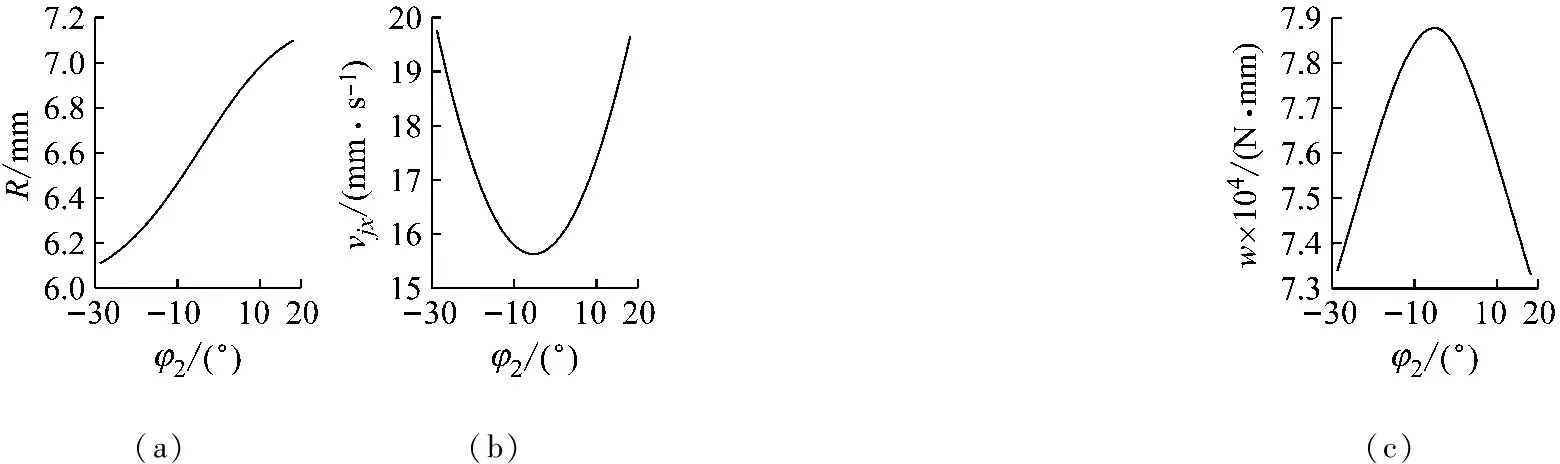
倾斜式双滚柱包络环面蜗杆传动当量曲率半径R、卷吸速度vjx和单位长度上的载荷w从啮入到啮出的变化曲线,如图2所示。从啮入到啮出,当量曲率半径逐渐增大,卷吸速度先减小后增大,单位长度上的载荷先增大后减小;在蜗杆喉部附近时卷吸速度达到最小值,单位长度上的载荷达到最大值。
2 粗糙齿面弹流润滑模型及数值解法
根据弹性流体动力润滑理论[15],倾斜式双滚柱包络环面蜗杆传动的蜗杆齿面与蜗轮齿面(即滚柱面)之间的线接触问题可以简化为一当量圆柱体与一平面的接触,如图3所示。
(a)(b)(c)
图2 当量曲率半径、卷吸速度和单位长度上的载荷
Fig.2 The equivalent curvature radius, entrainment velocity and load per contact length
2.1 线接触弹流润滑的基本方程

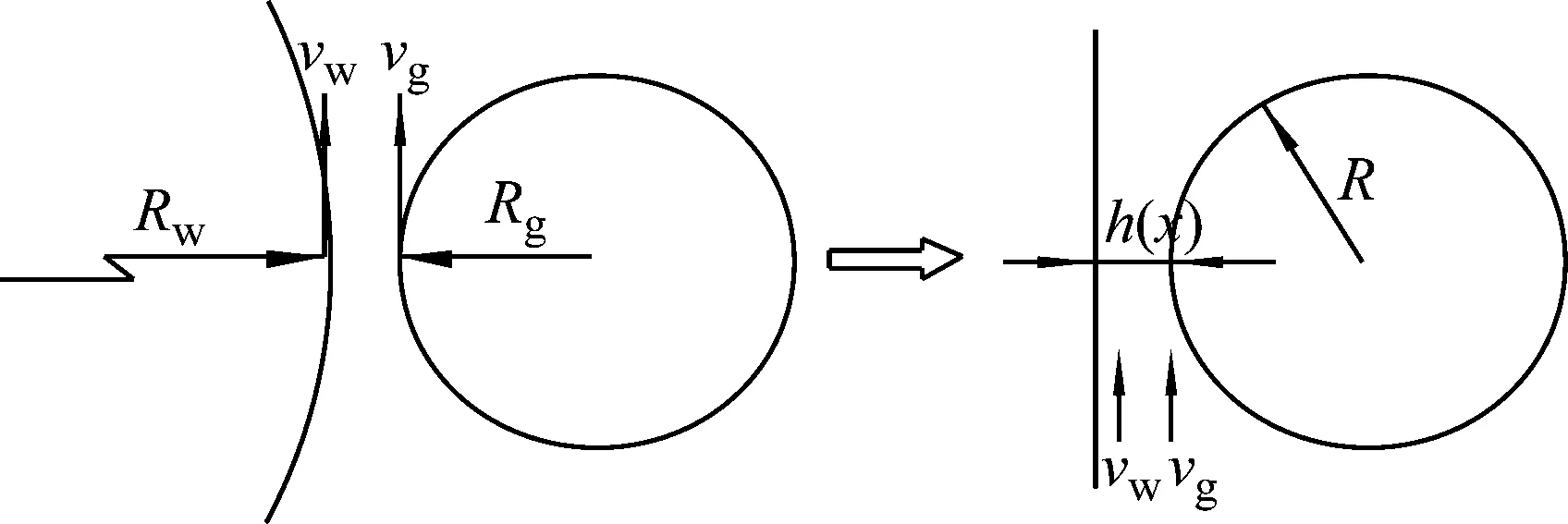
图3 线接触简化模型Fig.3 The line contact simplified model
根据牛顿流体弹流润滑模型,等温线接触弹流润滑的基本方程及无量纲化方程如下:
(1) Reynolds方程及无量纲化分别为
(5)
(6)
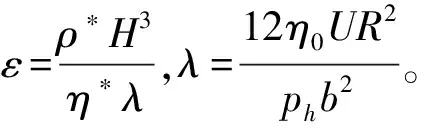
边界条件为
(2) 粗糙齿面线接触油膜厚度方程
假设蜗杆齿面和蜗轮齿面粗糙度纹理是横向的,蜗杆齿面和蜗轮齿面的粗糙度函数近似用余弦函数表示为[17]
(7)
式中:Aw、Ag分别为蜗杆齿面和蜗轮齿面粗糙度的幅值;lw、lg分别为蜗杆齿面和蜗轮齿面粗糙峰的波长;vw、vg分别为蜗杆齿面和蜗轮齿在啮合点处的速度。
考虑蜗杆齿面和蜗轮齿面粗糙度的影响,线接触油膜厚度方程为
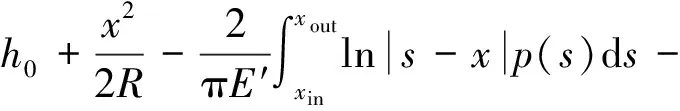
sw(s,t)-sg(s,t)
(8)
粗糙齿面线接触油膜厚度无量纲方程为
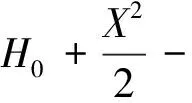
(9)
式中:H0为无量纲刚体的中心膜厚;S(X)为无量纲表面粗糙度函数
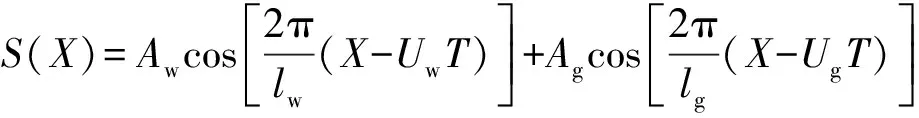
黏压方程[18]、密压方程[19]、载荷平衡方程的无量纲化方程分别如下
η*=exp{(lnη0+9.67)[(1+5.1×
10-9p)z-1]}
(10)
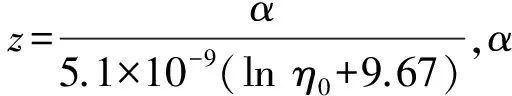
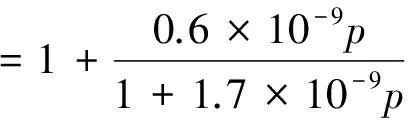
(11)
(12)
2.2 数值解法
考虑粗糙度,对倾斜式双滚柱包络环面蜗杆传动的弹流润滑数值问题,油膜压力的计算采用多重网格法,油膜厚度的计算采用多重网格积分法[20]。
(1) Reynolds离散方程
(13)
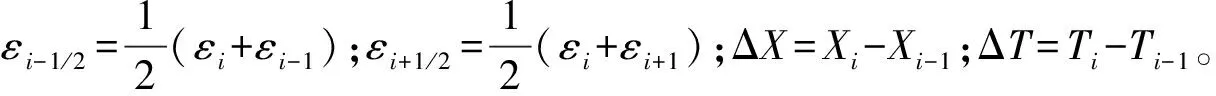
(2) 膜厚离散方程
高校心理健康教师队伍肩负着进行讲座、咨询、授课、团体辅导的重要职能,职能的多元化要求其专业性和规范化较高。一方面,高校需要加强心理健康教师的工作能力培养;另一方面,高校需要督导心理健康教师的心理成长,关心他们内心的感受和宣泄渠道等,切实保证心理健康教师心理健康。
(14)
式中:Kij为变形影响系数。
(3) 载荷离散方程
(15)
数值计算流程图,如图4所示。图4中ω为松弛迭代因子。采用数值稳定性较好的W循环,网格取六层网格,在最稠密的一层网格上划分961个节点,在计算过程中,根据压力的求解结果不断的对H0进行修正,并且在每一层网格上对压力的迭代采用Gauss-Seidel迭代,每一瞬时的压力和膜厚的迭代初值采用上一瞬时压力和膜厚的迭代结果。在计算求解过程中的迭代收敛准则为:压力Ep<0.001和载荷Ew<0.001。
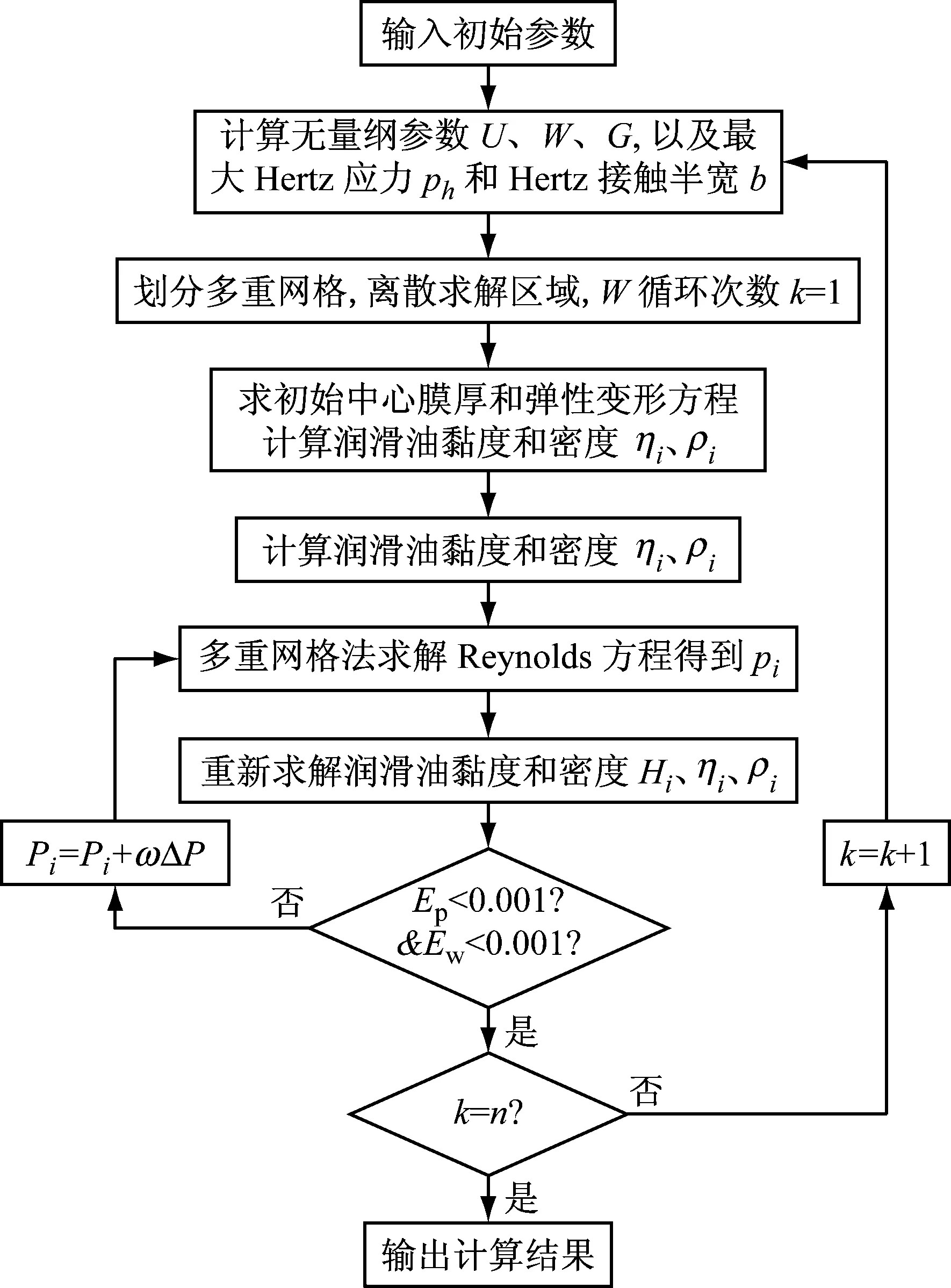
图4 线接触热弹流润滑数值计算流程图Fig.4 The flow char of line contact TEHL
3 数值结果及分析
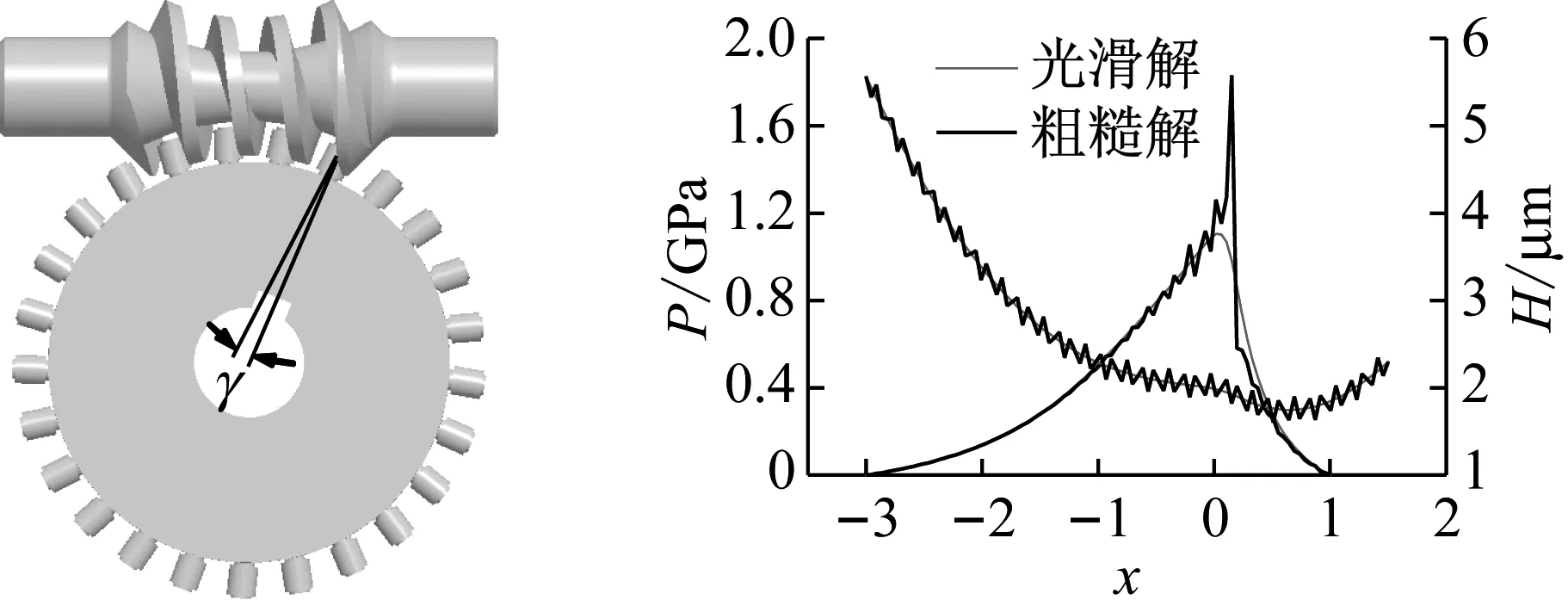
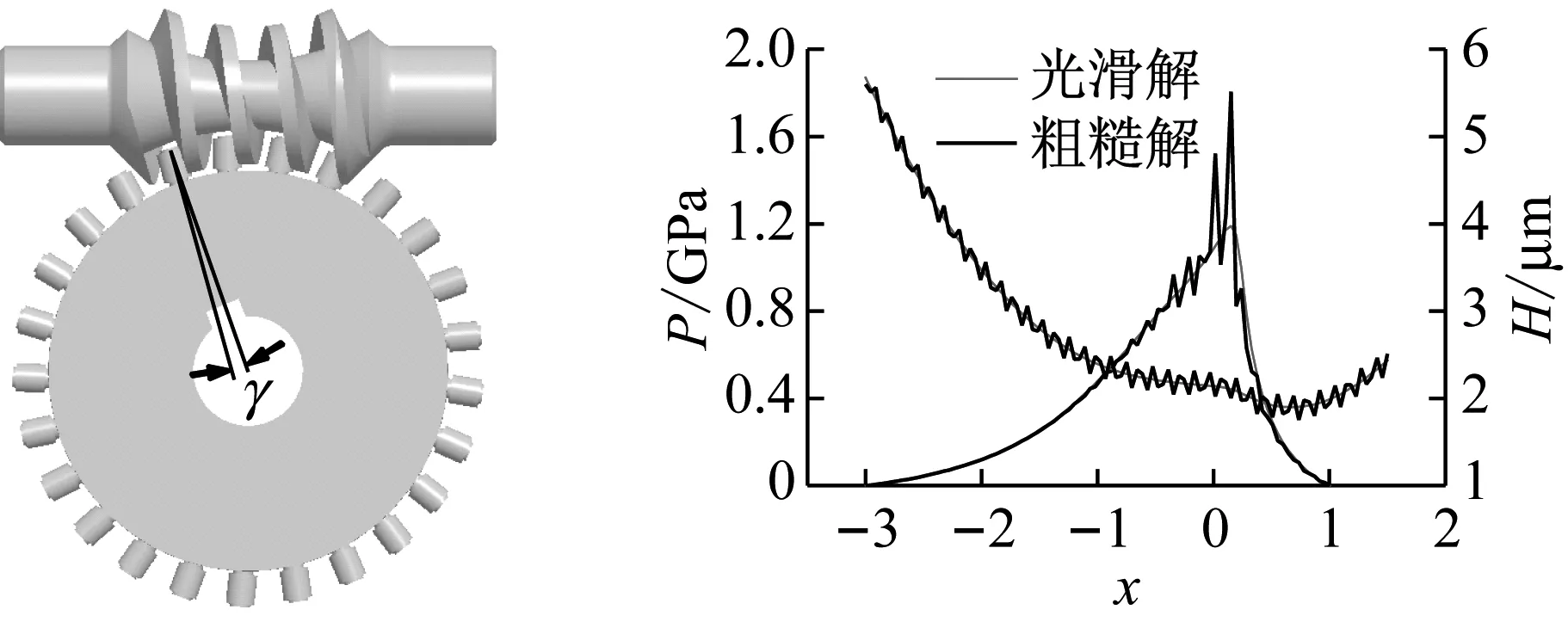
一倾斜式双滚柱包络环面蜗杆传动的基本设计参数及润滑油的相关参数,如表1所示。无量纲计算范围为X=[Xin,Xout]=[-3,1.5],输入功率P=5 kW,输入转速n1=1 450 r/min,Aw=Ag=0.06 μm,lw=lg=12 μm,蜗杆和蜗轮的材料参数:μ1=μ2=0.3、E1=E2=210 GPa。以右旋蜗杆传动为例,将某一个啮合齿对从啮入到啮出分为100个瞬时进行计算,粗糙解和光滑解的倾斜式双滚柱包络环面蜗杆传动在单齿啮合、双齿啮合、三齿啮合、四齿啮合的不同时刻的油膜压力和油膜厚度分布,如图5所示。
由图5可知,某一啮合齿对从啮入到啮出,光滑解和粗糙解的油膜压力峰值先增大后减小,油膜厚度先减小后增大。在主要承载区,每一个粗糙峰都会引起一个局部的油膜压力峰,粗糙度引起的油膜压力的波动最为剧烈,特别是在啮合的中间过程中,而油膜厚度的波动却不是很剧烈,这是因为油膜厚度的变化是在油膜压力的作用下存在滞后作用产生的,可见粗糙度对该传动副的润滑是不利的。另外,粗糙解的油膜压力和油膜厚度的波动都是在光滑解的附近波动。对比光滑解,粗糙解的最小油膜厚度比光滑解的计算结果有所减小,最大油膜压力峰值比光滑解的计算结果增大了很多。在单齿啮合和四齿啮合的时刻油膜厚度较大,三齿啮合的时刻,油膜厚度最小。

表1 传动副及润滑油相关参数Tab.1 This worm drive parameters and propertiesof lubricant
(a)

(b)

(c)
(d)图5 不同啮合点处的油膜压力及油膜厚度Fig.5 The pressure and thickness at different contact points
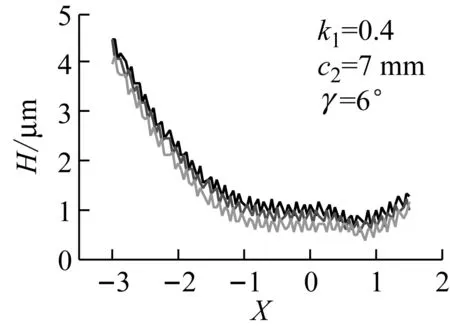
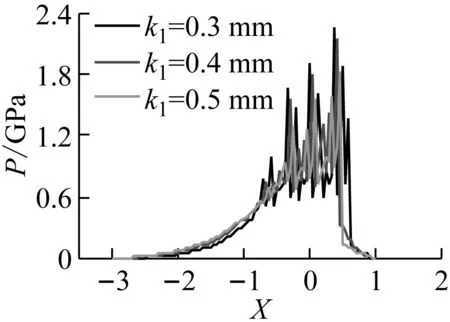
当设计参数:滚柱半径、喉径系数、滚柱偏距和倾斜角取不同值,其他参数不变时,该传动副在三齿啮合的时刻,设计参数对粗糙度下的油膜压力和油膜厚度的影响如图6~图9所示。从图6~图9中可知,随着滚柱半径、滚柱偏距和倾斜角的增大,油膜压力的波动越剧烈,最大压力值增大,油膜厚度减小。喉径系数过小时, 油膜压力的波动越剧烈,最大压力峰值越大,油膜厚度越小。喉径系数对油膜压力和油膜厚度的影响最大,滚柱偏距和滚柱半径次之,倾斜角对油膜压力和油膜厚度的影响最小。

(a)
(b)图6 滚柱半径对油膜压力和厚度的影响
Fig.6 Influence of roller radius on the oil film pressure and thickness
(a)
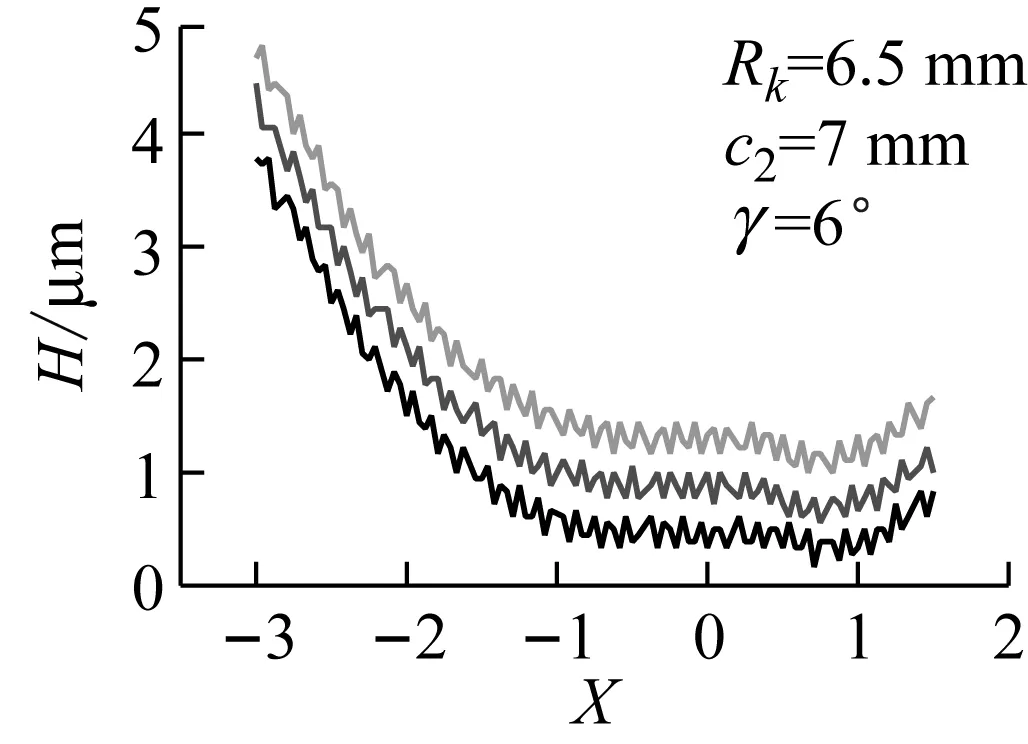
(b)图7 喉径系数对油膜压力和厚度的影响
Fig.7 Influence of orifice coefficient on the oil film pressure and thickness
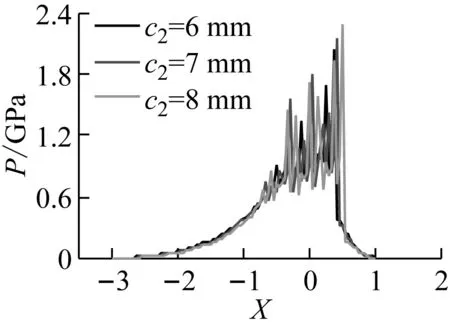
(a)

(b)图8 滚柱偏距对油膜压力和厚度的影响
Fig.8 Influence of offset distance on the oil film pressure and thickness

(a)
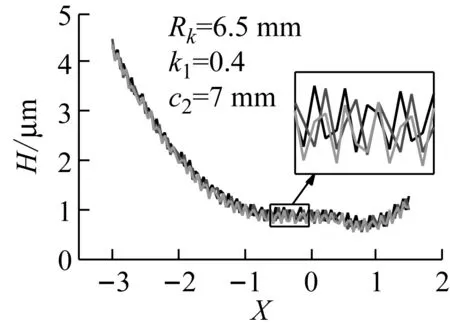
(b)图9 倾斜角对油膜压力和油膜厚度的影响Fig.9 Influence of inclined angler on the oil film pressure and thickness
4 结 论
本文在倾斜式双滚柱包络环面蜗杆传动啮合理论和弹性流体动力润滑理论的基础上,建立了该传动副的简化弹流模型,采用多重网格技术对考虑传动副粗糙度时的等温线接触弹流润滑问题进行了求解,得到不同啮合点处的油膜压力和油膜厚度,并分析了设计参数对油膜压力及油膜厚度的影响。
(2) 粗糙解的最小油膜厚度比光滑解的计算结果小,最大油膜压力峰值比光滑解的计算结果有所增大,粗糙度对该传动副的润滑是不利的。
(3) 在第三个齿开始啮入的时刻,油膜压力峰值最大,粗糙度将会造成油膜厚度减小变薄,形成润滑的危险区。
(4) 滚柱半径、滚柱偏距和倾斜角过大,喉径系数过小时,越不利于动压油膜的形成,对传动副的润滑越不利,可以通过对传动副的弹流润滑的优化计算合理选择传动副的设计参数。
参 考 文 献
[1] 柳在鑫,王进戈,张均富,等.交错轴双滚子包络环面蜗杆传动啮合分析[J].四川大学学报(工程科学版),2012,44(4): 221-225.
LIU Zaixin, WANG Jinge, ZHANG Junfu, et al. Meshing analysis of non-parallel double-roller enveloping hourglass worm gearing[J]. Journal of Sichuan University (Engineering Science Edition), 2012, 44(4): 221-225.
[2] 柳在鑫,王进戈,张均富.倾斜式双圆柱滚子包络环面蜗杆传动几何特性分析[J].北京理工大学学报,2013,33(5): 459-464.
LIU Zaixin, WANG Jinge, ZHANG Junfu. Geometrical characteristics analysis of non-parallel double-roller enveloping hourglass worm gearing[J]. Transactions of Beijing Institute of Technology, 2013, 33(5): 459-464.
[3] 柳在鑫,王进戈,张均富,等.倾斜式双滚子包络环面蜗杆副承载能力研究[J].高技术通讯,2013,23(5):491-496.
LIU Zaixin, WANG Jinge, ZHANG Junfu, et al. Research on the load carrying capacity of inclined double-roller enveloping hourglass worm gears[J] Chinese High Technology Letters, 2013, 23(5): 491-496.
[4] 邓星桥,王进戈,张均富,等.无侧隙双滚子包络环面蜗杆真实啮合齿面的理论研究[J].西南交通大学学报,2010,45(2): 222-226.
DENG Xingqiao, WANG Jinge, ZHANG Junfu, et al. Theoretical study on real tooth surface of non-backlash double-roller enveloping hourglass worm[J]. Journal of Southwest Jiaotong University, 2010, 45(2): 222-226.
[5] WANG Jinge, HE Rong, DENG Xingqiao, et al. Manufacturing technology study on non-backlash double-roller enveloping hourglass worm[J]. Applied Mechanics and Materials. Trans Tech Publications, 2013, 415: 524-528.
[6] 张光辉,王进戈,杨念增.滚锥包络环面蜗轮副的研制与试验[J].重庆大学学报,1992,15(5):8-11.
ZHANG Guanghui, WANG Jinge, YANG Nianzeng. Development and test on rolling cone enveloping hourglass worm pair[J]. Journal of Chongqing University, 1992, 15(5): 8-11.
[7] 王进戈,张均富,王强.滚锥包络环面蜗杆传动的润滑状态分析[J].哈尔滨工业大学学报,2005,37(7):940-942.
WANG Jinge, ZHANG Junfu, WANG Qiang. Lubrication states analyses on rolling cone enveloping hourglass worm gearing[J]. Journal of Harbin Institute of Technology, 2005, 37(7): 940-942.
[8] 王优强,卞荣.连续波状粗糙度对直齿轮热弹流润滑的影响[J].机械工程学报,2009,45(8):112-118.
WANG Youqiang, BIAN Rong. Influence of surface roughness wave on thermal elastohydrodynamic lubrication of involute spur gears[J]. Journal of Mechanical Engineering, 2009, 45(8): 112-118.
[9] CHEN Yonghong, ZHANG Guanghui, CHEN Bingkui, et al. A novel enveloping worm pair via employing the conjugating planar internal gear as counterpart[J]. Mechanism and Machine Theory, 2013, 67: 17-31.
[10] SIMON V. EHD lubrication characteristics of a new type of ground cylindrical worm gearing[J]. Journal of Mechanical Design, 1997, 119(1): 101-107.
[11] 许立忠,杨育林,黄真.超环面行星蜗杆传动弹流润滑状态研究[J].机械工程学报,2002,38(9):114-117.
XU Lizhong, YANG Yulin, HUANG Zhen. EHL condition for toroidal drive[J]. Journal of Mechanical Engineering, 2002,38(9): 114-117.
[12] SHARIF K J, KONG S, EVANS H P, et al. Contact and elastohydrodynamic analysis of worm gears Part 1: Theoretical formulation[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2001, 215(7): 817-830.
[13] 汪久根,朱聘和.蜗杆传动的润滑分析[J].润滑与密封, 2005,167(1):3-4.
WANG Jiugen, ZHU Pinhe. Study on lubrication in worm gear transmission[J]. Lubrication Engineering, 2005, 167(1): 3-4.
[14] 邱昕洋,张光辉,秦大同.钢制平面蜗轮传动弹流润滑分析[J].重庆大学学报,2010,33(3):24-29.
QIU Xinyang, ZHANG Guanghui, QIN Datong. Analysis of elastohydrodynamic lubrication of steel planar wormgear drive[J]. Journal of Chongqing University, 2010, 33(3): 24-29.
[15] 温诗铸,杨沛然.弹性流体动力润滑[M].北京:清华大学出版社,1992.
[16] 黄平.润滑数值计算方法[M].北京:高等教育出版社,2012.
[17] 张建军,刘晓玲,杨沛然.单粗糙峰的时变等温线接触弹流润滑分析[J].润滑与密封,2005(2):67-71.
ZHANG Jianjun, LIU Xiaoling,YANG Peiran. An analysis of tmie-dependent isothermal line contact elastohydrodynamic lubrication problems with single asperities[J]. Lubrication Engineering, 2005 (2): 67-71.
[18] HSU C H, LEE R T. An efficient algorithm for thermal elastohydrodynamic lubrication under rolling/sliding line contacts[J]. Journal of Tribology, 1994, 116(4): 762-769.
[19] GUILBAULT R. A simplified thermal analysis of elastohydrodynamic contacts[J]. Journal of Tribology, 2013, 135(2): 021502.
[20] VENNER C H, TEN NAPEL W E, BOSMA R. Advanced multilevel solution of the EHL line contact problem[J]. Journal of Tribology, 1990, 112(3): 426-431.

