基于二阶滑模速度控制器的船用六相永磁同步电机矢量控制系统性能研究＊

刘 超，曹兆锦，常俸瑞

（1.南京理工大学泰州科技学院，泰州225300；2.广东电网有限责任公司湛江供电局，广东湛江524005）

1 引言

永磁同步电机（PMSM）随着日益更新的控制技术的进步与高性能永磁体的发展，逐渐代替了传统的电励磁同步电机，在航空航天业、新能源汽车及船舶工业等领域占据了一席之地，但国外发达国家的永磁电机处于行业的领先地位，随着中国制造2025的即将来临，国产永磁同步电机获得了高速发展，行业的前景较为乐观。相较于传统的三相永磁同步电机控制系统，六相永磁同步电机相永磁同步电机控制系统凭借其优越的性能、高可靠性及强大的容错能力受到国内外诸多学者的注目，其在船舶建造行业的发展尤为迅速。

船用六相永磁同步电机作为一种非线性、高耦合、多变量的复杂控制系统，需要一种高效的控制方法，实现对六相永磁同步电机的精确控制，以达到提高六相永磁同步电机的性能的目的。高精度高性能的控制系统要求电机的输出响应速度快，转矩脉动稳定，并且抗干扰能力较强，滑模控制（SMC）作为一种优秀的控制方法，具有速度较快，响应时间短等多种优点，经过国内外学者的推广与发展，滑模控制在伺服控制系统中取得较好的结果。

本文采用一种控制精度高的二阶滑模控制器对六相电机速度环进行控制，在Mtalab内搭建了二阶滑模速度控制器模型，将其仿真的波形与传统PI速度控制器进行比较，得到结论:二阶滑模速度控制器具有比PI控制更加优秀的速度动态响应能力，使电机系统的鲁棒性、抗干扰能力更强。

2 建立六相永磁同步电机数学模型

六相永磁同步电机作为一种多维度、多变量、高耦合的非线性系统，其数学模型与实际情况有许多差别，为了方便简化分析电机的数学模型，当对电机做出一些条件假设，方便建模:

①忽略磁铁的磁滞效应、涡流效应及饱和效应；

②电机的定子绕组应均匀分布，且不急齿槽效应；

③不考虑磁场中空间高谐次波对系统的影响，使磁势按正弦分布。

根据以上所确立的先行条件，对六相永磁同步电机建立经过基于矢量空间解耦（VSD）办法的坐标变换后的数学模型，使电机具有x-y、d-q两个子空间。

a.六相PMSM空间电压方程:

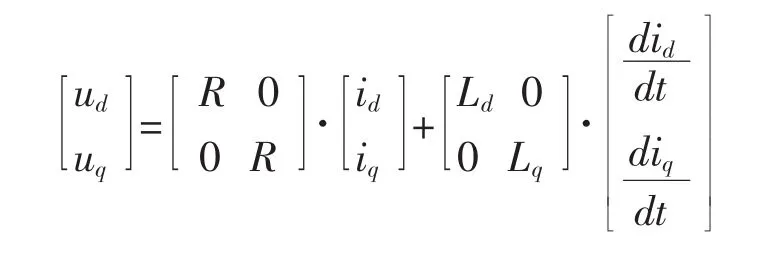
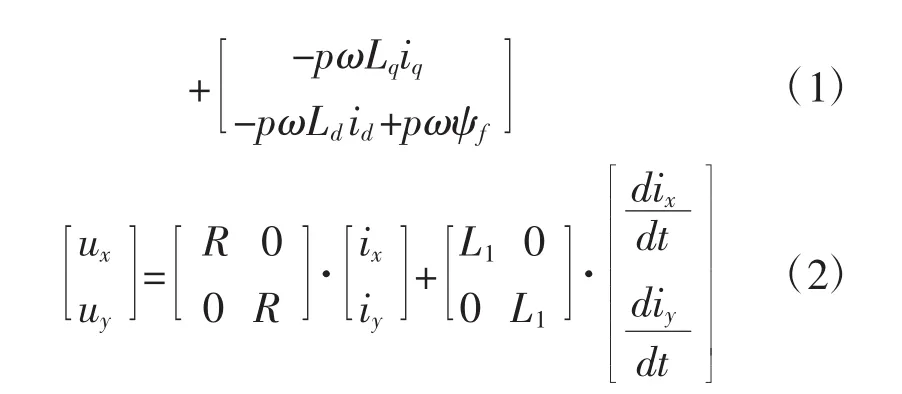
b.六相PMSM运动方程:

c.六相PMSM转矩方程:

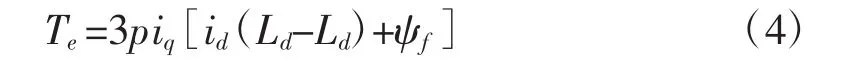
其中:ud、uq、ux、ux表示为 d-q、x-y 定子电压；id、iq、ix、iy表示定子电流；R表示定子电阻；L1表示漏感；p表示极对数；ψf表示磁链；ω表示角速度；Te表示转矩；TL表示负载转矩（多种转矩:如齿槽转矩、电源波动等）；J表示转动惯量。

根据公式（1）（2）的方程可以看出六相PMSM数学模型的完全解耦，则六相PMSM完全可以采用与三相PMSM的iq＝0控制策略相同的控制策略，即在 x-y、d-q 两个子空间内使 id＝ix＝iy＝0。

基于id＝ix＝iy＝0的矢量控制的六相永磁同步电机的速度控制系统主要分为六大模块:

①一个速度环控制器和四个电流环控制器；

②坐标变换模块；

③六相PWM模块；

④逆变器模块；

⑤编码器模块；

⑥六相永磁同步电机模块。

3 二阶滑模控制

滑模变结构控制广泛被应用在电机智能控制的领域，而六相永磁同步电机是一种较为复杂的非线性系统，将关于特殊的非线性控制策略的滑模控制算法引入到六相电机的复杂系统中，有利于发挥出滑模控制的算法简便，稳定性好的优势。在滑模研究的发展中，有终端滑模、分数阶滑模、变阶次滑模等多种各具特色的滑模控制被衍生而来，其优劣并存。本文采用基于Super-twisting算法的二阶滑模速度控制，其能够使传统SMC系统中的抖振现象被有效抑制，并且没有减弱其他优点，将速度环上的传统PI控制器代替为Super-twisting二阶滑模控制器，在一定程度上提高了六相电机控制系统的整体性能。

3.1 Super-twisting 算法

Super-twisting算法作为二阶滑模控制算法中的一种，在相平面上的移动轨迹逐渐逼近原点处，滑模面附近的控制量不断收敛，直到系统的等效控制，从而解决了了传统滑模的抖振问题。一般的动态控制系统为:

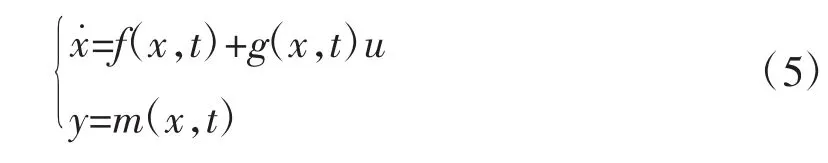
式中:x—状态变量

f、g、m —未知函数

u—连续控制输入量

Super-twisting算法的相平面的轨迹逐渐收敛逼近至原点，因其轨迹图是螺旋式结构，又被称为超螺旋算法。其控制律可如此设计:

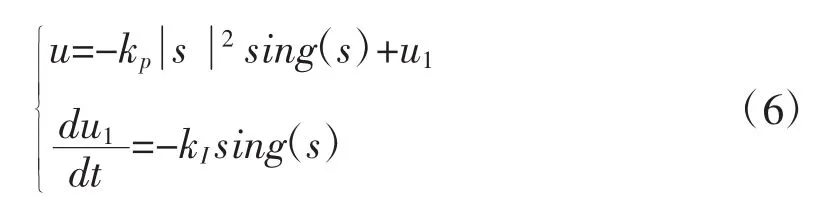
式中:kp、kI为滑模增益。

Super-twisting滑模控制器在滑模面上收敛的充要条件:

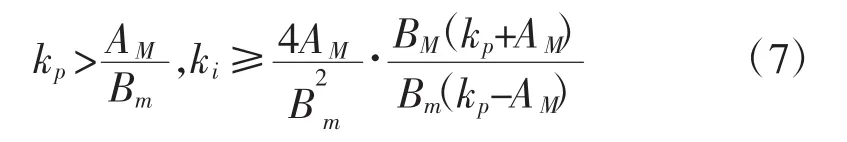
3.2 控制器设计

定义六相PMSM状态变量:

式中:ω1为参考转速，其为常数，ω为实际转速。

式中:c为大于0的设计参数。

对式（8）进行求导:

由式（1）、（2）、（3）化简可知:

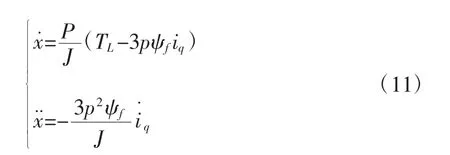
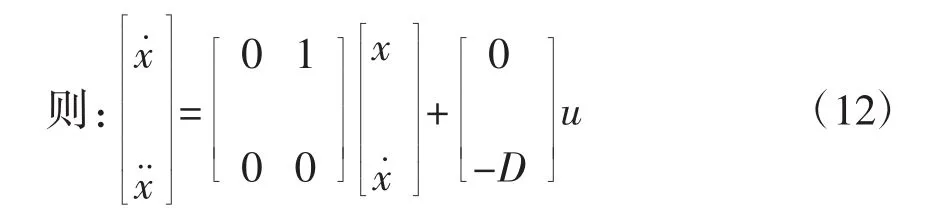
式（9）可得:

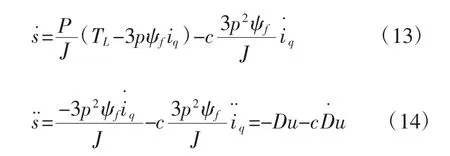
结合式（5）和式（14），对式（5）再次求导，由 A和B分别是输出y的二阶导数的上下限知，不难看出，极对数、磁链等都有边界，所以均可以通过调节滑模增益kp、kI来使系统达到控制要求。

将速度控制器的设计参数值取0.5时，控制器方程为:

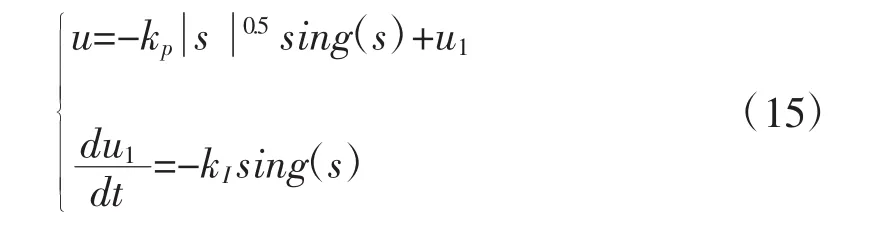
4 建模与仿真

根据图1所示的六相永磁同步电机矢量控制系统的结构图，利用Matlab/Simulink工具箱对六相永磁同步电机二阶滑模速度控制系统进行仿真研究，给定电机转速60rad/s，将传统PI控制器的输出波形与本文的二阶滑模速度控制器进行对比，并且将给定转速在0.2s时将转速由60rad/s降落至30rad/s，比较两者的优劣。

本文所采用的六相PMSM参数为:极对数p＝3，磁链 ψf＝0.68wb，转动惯量 J＝0.015kg·m2，电感 Ld＝Lq＝8.8mH，定子电阻 R＝1.4Ω，阻尼系数为 0。在空载下运行电机，采用ode23tb算法，仿真时间为0.4s。取 kp＝3，kI＝5，C＝0.1。

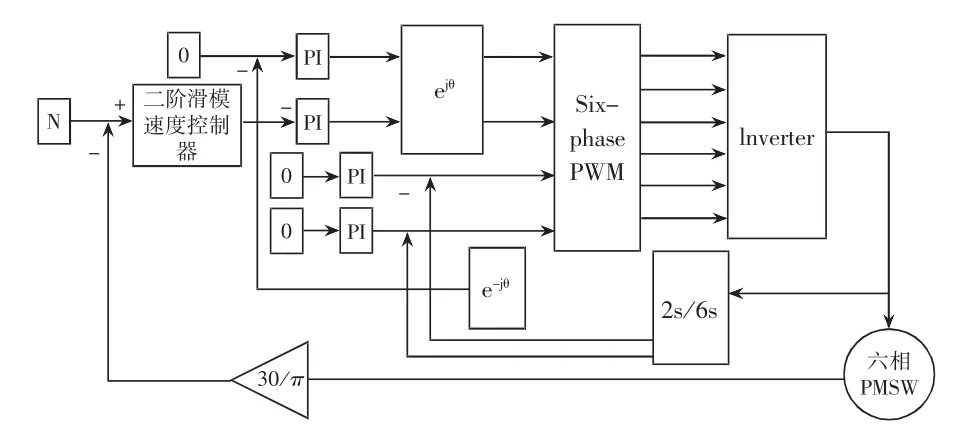
图1 六相永磁同步电机二阶滑模速度控制系统

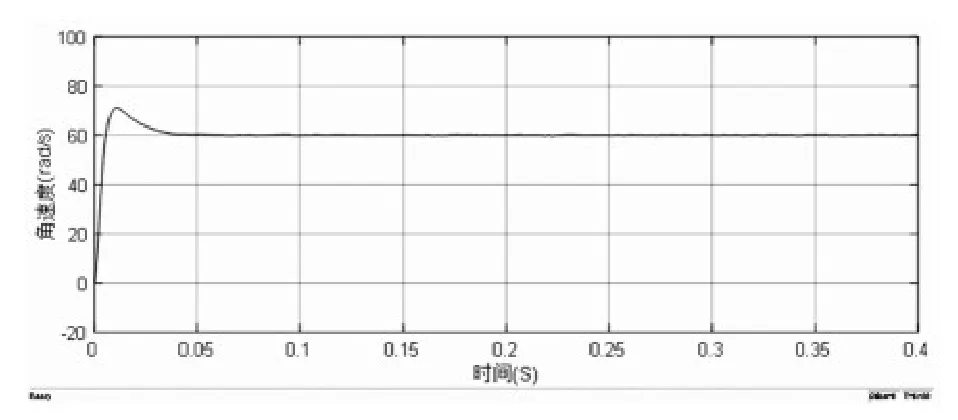
图2 PI控制角速度变化曲线

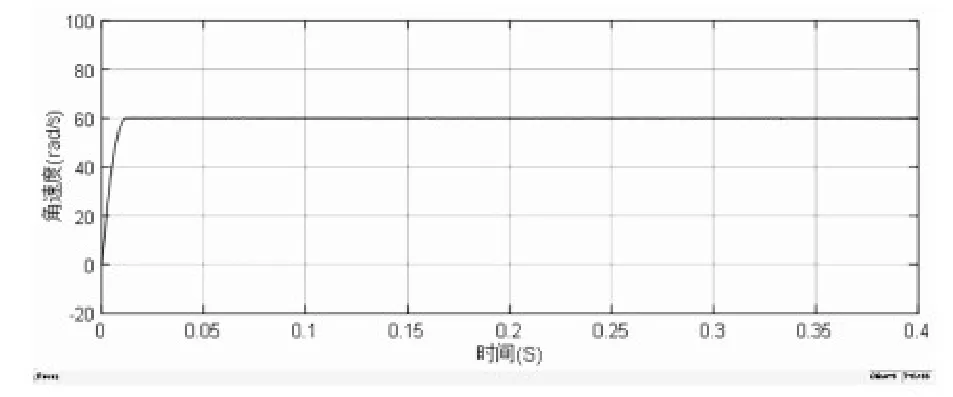
图3 二阶滑模控制角速度变化曲线

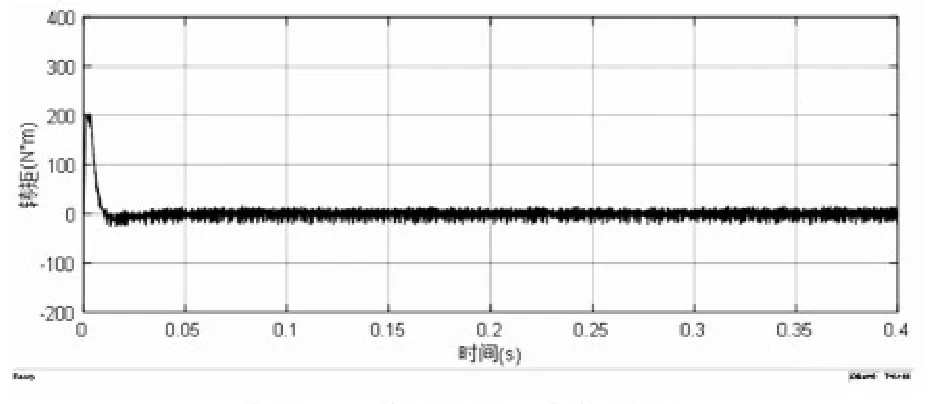
图4 PI控制转矩变化曲线

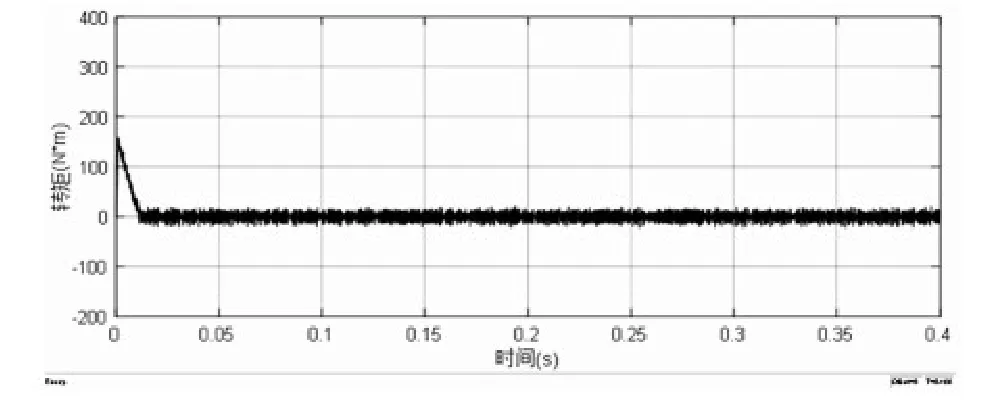
图5 二阶滑模控制角速度变化曲线

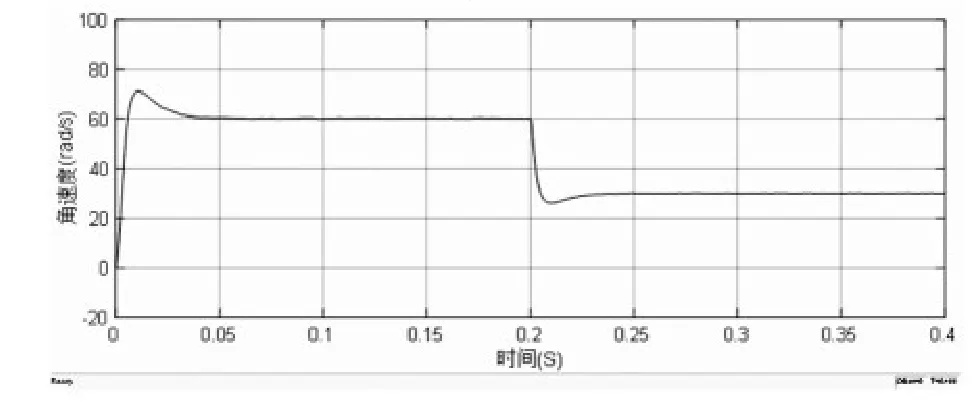
图6 PI控制转速突变时角速度变化曲线

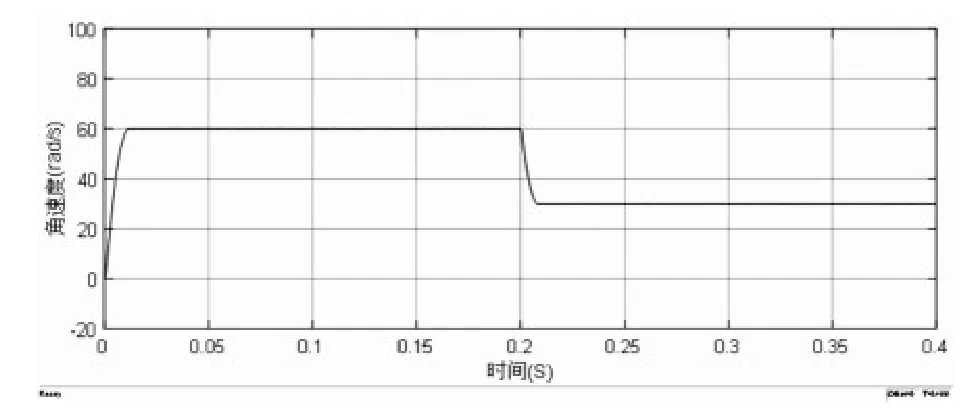
图7 二阶滑模控制转速突变时角速度变化曲线

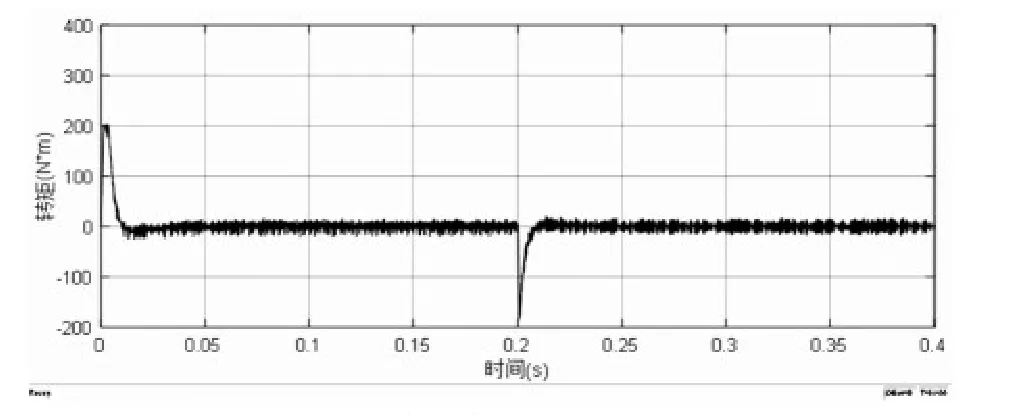
图8 PI控制转速突变时转矩变化曲线

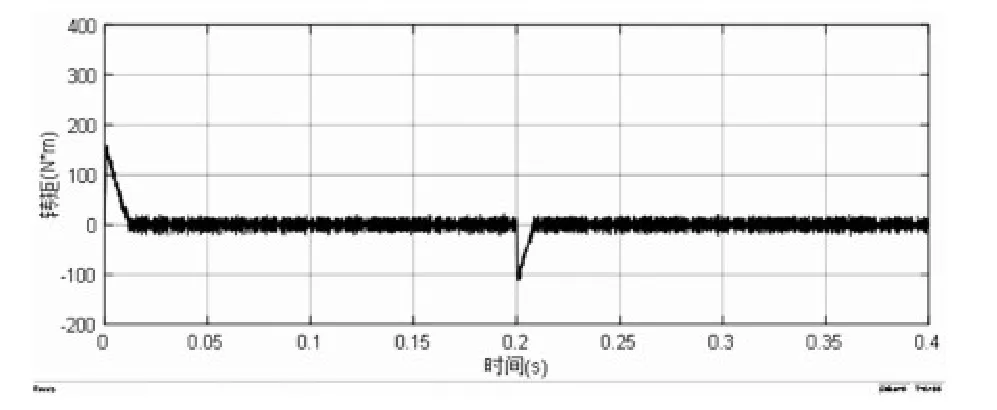
图9 二阶滑模控制转速突变时转矩变化曲线

从图2至图5的对比可以看出，二阶滑模控制下的电机没有超调量，运行较PI控制更加稳定，速度响应更快，二阶滑模控制下的电机转矩波动较小，初始转矩的脉动没有PI控制下脉动高；从图7至图9的详细对比可以看出，在转速突变的过程中，二阶滑模控制能够相对于PI控制的响应速度更快，鲁棒性更好，转速更平稳，并且在0.2s时，二阶滑模的转矩脉动比PI控制更小；以上现象足够说明二阶滑模速度控制器的突出的优越性。

5 结论

本文详细研究了基于Super-twisting算法的二阶滑模速度控制器，以及六相永磁同步电机的矢量控制系统，在Matlab/Simulink工具箱的基础上进行仿真研究，验证了模型的正确性。综上所述，二阶滑模速度控制系统有如下优点:（1）二阶滑模速度控制器在运行时解决了传统滑模的抖振问题；（2）在六相永磁同步电机速度控制系统中，二阶滑模有着响应速度快，初始转矩脉动小，鲁棒性强等无与伦比的优点；（3）没有PI控制器在刚开始运动时的超调量；（4）在六相PMSM中，当给定转速突变时，二阶滑模的强大的稳定性、抗干扰能力得到了验证。