多级压气机气动弹性不稳定性计算方法综述
(Vibration UTC,Mechanical Engineering,Imperial College London,London,UK)
0 Introduction
Unsteady turbulent high-speed compressible flows often give rise to complex aeroelasticity phenomena by influencing the dynamic behaviour of structures on which they act.Under certain conditions,the energy transfer from the fluid to the structure can cause excessive vibration levels and structural integrity may be compromised.The problem is particularly severe for gas turbines where virtually all blade rows are susceptible to aeroelasticity effects either by inherent self-induced motion(flutter)or by response to aerodynamic flow distortions and blade wakes(forced response).The most complex and the least understood aeroelasticity phenomena occur in multi-stage core compressors,the subject of this paper,because of their wide operating envelope.During engine developmentprogrammes,costly structural failures are known to occur because of a mixture of aeroelastic instabilities such as acoustic resonance,flutter,forced response,rotating stall,surge,etc.
As turbomachinery blade aerofoils are thinned to improve performance,reduce weight and reduce cost,aerodynamic and aeroelastic challenges such as surge and flutter become more predominant.Moreover,the use of titanium blade-integrated-disks(blisks)is becoming more common in modern civil aero-engine designs.Such structures have a very low mechanical damping in contrast to traditional bladed-disk assemblies.For such structures,the main source of damping to the blade comes from the air flow,which highlights the importance of accurate prediction of blade response due to aerodynamic forces.Large magnitude blade deflection induced by high loading can cause rubbing between blade tip and the casing,or more destructively the contact between rotor and stator blades.Aeroelastic instabilities,such as flutter and non-synchronous vibrations,may also couple with aerodynamic flow disruptions,driven by the emergence of stall cells or flow reversal during surge.It is thus important to be able to predict the instabilities at such difficult flow conditions at the early design or testing stages of an engine.Aerodynamic and aeroelastic experimental tests at such conditions,especially for multistage high speed machines,are usually very expensive in time and financial cost,hence remain a challenging task.Computational methods such as 3D unsteady Reynoldsaveraged Navier-Stokes(URANS)have shown to be capable of providing a more informative understanding of the flow physics in such conditions with greatly reduced cost.
This paper reviews some of the work on aeroelastic instabilities in multi-stage core compressors driven by stall,surge,forced response and flutter carried out by reference[1-4].In the following sections,the physical phenomena triggering compressor instability and possible numerical approaches for modelling them are highlighted for each case.
1 FLow solver
The CFD code used for this work is AU3D,which is a three-dimensional,time-accurate,viscous,finitevolume compressible flow solver. For detailed information the reader is referred to[5].The unsteady flow cases are computed as URANS,with the basic assumption that the frequencies of interest are sufficiently faraway from the frequenciesofturbulentflow structures.The flow variables are represented on the nodes of a generic unstructured grid and numerical fluxes are computed along the edges of the grid.The numerical fluxes are evaluated using Roe’s flux vector difference splitting to provide matrix artificial dissipation in a Jameson-Schmidt-Turkel(JST)scheme.The overall solution method is implicit,with second-order accuracy in space and time.For steady-state flow computations,the solution is advanced in pseudo-time using local time stepping,while dual time stepping is used for unsteady computationsto preservestability athigh Courant numbers.For steady-state flow calculations,solution acceleration techniques,such as residual smoothing and local time stepping are employed. The current computations use the one-equation Spalart-Allmaras turbulence model proposed by[6].The parameters in Spalart-Allmaras have been adjusted on previous fans to getgood agreementnear the stability limit;the parameters are held constant in all the present work.The resulting CFD code has been used over the past 20 years for flows at off-design conditions with a good degree of success[7-9].
2 Rotating Stall Induced Vibration
Rotating stall is a disturbance that is local to the compressor blade rows,which is characterized by a circumferential non-uniform flow deficit,with one or more stall cells propagating around the compressor circumference at a fraction of the shaft speed,typically between 20%and 60%.In fully developed rotating stall,the overall flow through the compressor is constant in time,with the stall cells redistributing the flow around the annulus.From an industrial perspective,it is important to understand the factors that influence changes in stall characteristics as it may result in moving from a safe operating regime to one that causes rotor blade failure.These effects are normally assessed by engine strain gauge tests,which are used to map out stall boundaries.However,due to the high cost of these tests and the limited scope for varying engine configuration and operation,efficient computational methods that minimise rig and engine testing becomes vital.The numerical modelling of such a situation remains a formidable challenge as the analysis must be able to represent accurately not only the aerodynamic and structural properties of a large number of blade rows but also the interactions through these.
In the work by reference[2],a methodology was developed which can predict the effects of multi-lobe rotating stall on blade vibration levels.Of particular importance is to link the variable-vane scheduling to the number,size,distribution,and speed of rotating stall cells so that the critical modes of vibration can be identified and avoided.To achieve that objective,an eight-stage compressor was chosen where the first three stator blade rows have variable-angle vanes.The domain used for steady state computation is shown in Figure 1.Two vane settings,namely datum-scheduled(DS)and mal-scheduled(MS),were investigated because of the availability of experimental data for these two conditions.
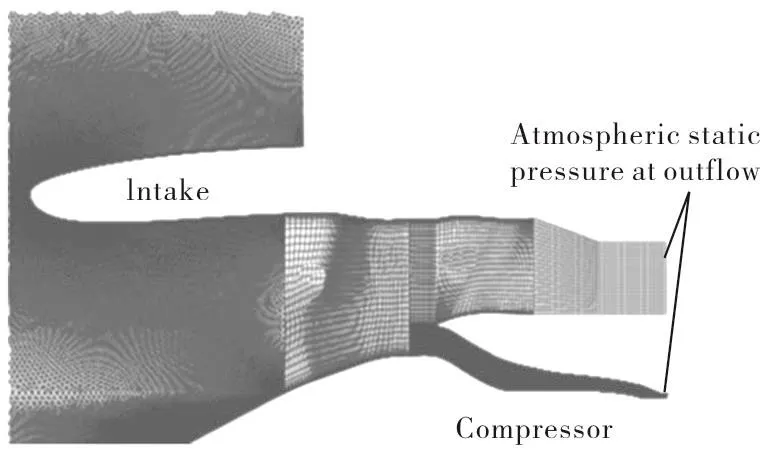
Fig.1 Steady state computational domain.
In the steady-flow computations,the entire domain was modelled using a single-passage approach with mixing planes.Mass flow through the bypass and core are controlled by means of nozzle with atmospheric static exit boundary conditions.Steady state results show that there is a strong interaction between the core and the lowpressure (LP) compressor domains: the massive separation around the Rotor 1 tip affects the flow at the fan root,which in turn affects the flow into the core compressor.Therefore,the inclusion of the LP domain is critical for the correct prediction of the onset of rotating stall.Moreover,the separated flow region on Rotor 1 extends much further axially and radially for the MS case.
For the unsteady computations,the first nine blade rows of the compressor were modelled in a wholeannulus fashion,whereas the rest of the compressor as well as the LP domain were modelled using single passages. This approach was adopted to allow circumferentially non-uniform flow disturbancesto develop in the full annulus blade rows,which is crucial in the inception and development of rotating stalls.The variation of the static pressure upstream of Rotor 1 after 13 engine rotations is shown in Figure 2.It is seen that the flow looks symmetric for the DS case,i.e.,no sign of rotating stall.On the contrary,a non-symmetric pattern,i.e.rotating stall,develops for the MS case.The variations of the instantaneous static pressure upstream of Rotor 1 along the circumference at 70%and 90%heights are shown in Figure 3(a)together with the corresponding Fourier components.A close study of these figures reveals the existence of a 12-band rotating stall for the MS case.Moreover,the figure shows that the rotating stall is much stronger at 70%height.The unsteadiness due to rotating stall interacts with the assembly vibration modes,a feature that creates unsteady forcing on the blade.The Fourier components of the unsteady forcing for different nodal diameter(ND)modes arising from the blade 1F mode are shown in Figure 3(b).In the event of the two frequencies matching,the response in that mode is estimated to be about 20%of the chord length using a Q-factor damping value of 200,which corresponds to a structural damping loss factor of 0.5%.The above results are in a very good agreement with engine data.
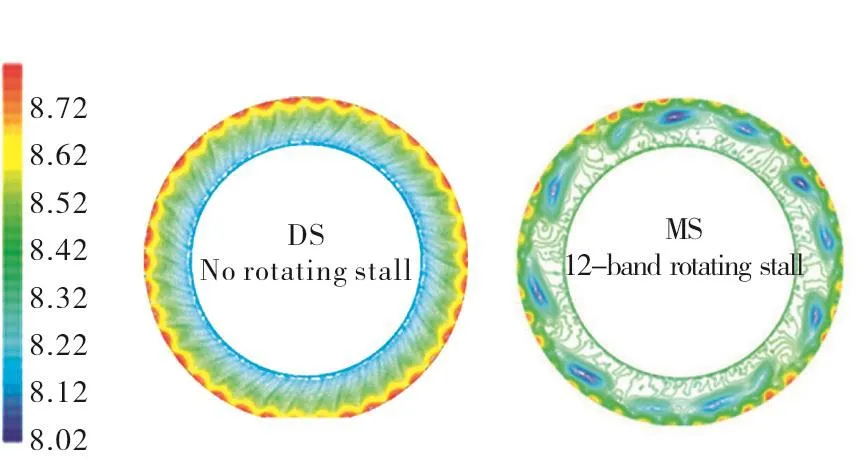
Fig.2 Instantaneous static pressure upstream of Rotor 1:DS vs MS.
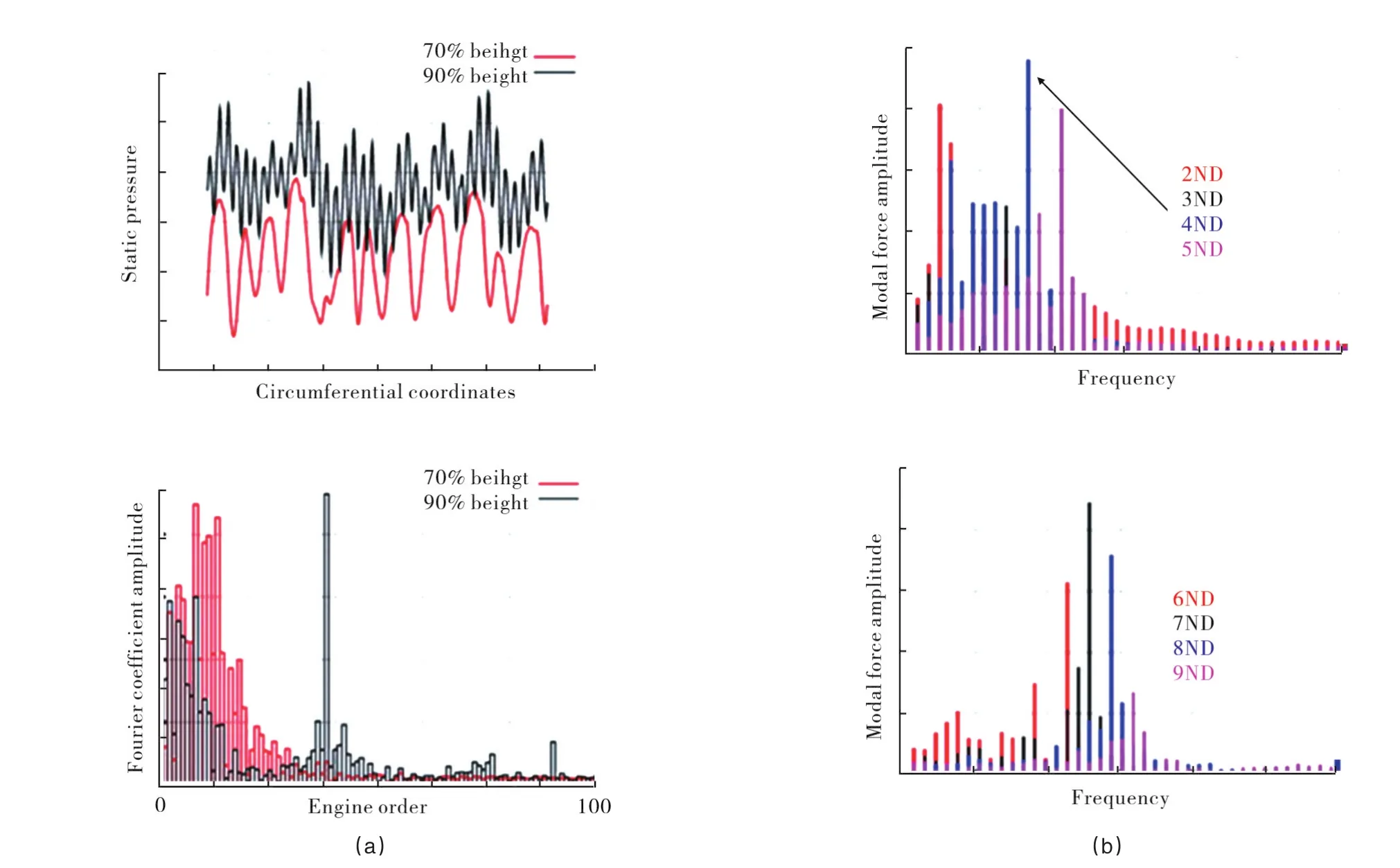
Fig.3 (a)Static pressure upstream of Rotor 1 and its Fourier components at 70%and 90%height;(b)Fourier components of forcing on the rotor blades.
3 Flutter in Deep Surge
In contrast to part-span rotating stall,surge is a global instability,which involves an axial oscillation of the flow inside the whole compression system,consisting of the blade rows as well as any ducting or plenum volume after the last blade row.Surge occurs in cycles where the flow oscillates throughout the compression domain as the downstream volume(combustor)is filled and emptied periodically.
This section summarises the modelling of a surge event by reference[2]using the same eight-stage core compressor as shown in the previous section.The domain used in the surge study,identical to that used in the steady state computations,isillustrated in Figure 1.The approach taken is based on the time-accurate version of the single-passage steady-state flow model where mixing planes are used at the blade row boundaries.The characteristic variables are imposed at the mixing plane and the number of conditions imposed is determined from the actualflow direction.Therefore,the interface boundaries can automatically change from inlet to exit or vice versa.A multi-bladerow single-passage analysis is a“reasonable”simplification from the full model and,in spiteofitspotentialshortcomings,which willbe discussed later regarding the modelling of rotating stall,it provides considerable insight to the flow behaviour during surge.It is assumed that full surge has developed and that the unsteadiness is mainly in the axial direction.This approach is useful to provide a first approximation to vane loading during surge.
Starting from a steady and stable solution,the nozzle at the back of the core compressor is gradually closed,until a situation is reached where the compressor is not able to produce the required pressure ratio and the flow becomes unstable and surges.The variation of negative axial velocity,indicative of stall regions,at mid-passage plane at six different time levels is shown in Figure 4(a).It is seen from this figure that there is no stall initially.As the time evolves,stall regions are formed and expand in the domain.The process continues until the whole compressor is filled with reversed flow and the flow starts to come out of the compressor.Due to the flow reversal,the volume upstream of the nozzle empties and the pressure at the end of compressor decreases.Hence,the required pressure rise across the compressor drops and consequently the compressor recovers from stall.With the filling of the volume,the pressure at the back of the compressor increases again,and the process above repeats itself.Surge occurs in cycles where the flow oscillates throughout the compression domain as the downstream volume combustor is filled and emptied periodically.Hence,the frequency of the surge is dictated by the size of the volume upstream of the nozzle.The time history of the mass flow/pressure ratio is shown in Figure 4(b),which shows the hysteresis loop for the compressor.It is obvious that the above procedure creates a significant amount of unsteadiness,and hence as a result of interaction with blade modes a large amount of unsteady forcing is produced.The time history of mass flow and forcing on the blade,as well as the Fourier components of the forcing,are shown in Figure 5.The forcing is for the first flapwise bending(1F)mode of the rotor assembly.It can be seen that,for such a chaotic event,the forcing on the blade almost repeats itself during each surge cycle.A Fourier transform of the forcing shows that all frequencies are present in the forcing and that the aeroelastic behaviour during surge can be viewed as an impulse response where all modes are excited.The highest forcing corresponds to the surge frequency,and it is determined by the size of the control volume.Furthermore,it can be seen from these figures that the steady(averaged)forcing on the blade changes and hence the blade twist is due to changes in the aerodynamic loading.

Fig.4 (a)Time history of negative axial flow at mid-passage;(b)Hysteresis loop for mass flow versus pressure ratio.

Fig.5 (a)Time history of mass flow and blade forcing;(b)Fourier components of forcing.
To further investigate the blade response during the surge event,a hybrid model is used for the flutter analysis of R5.In this method,apart from R5 which is modelled in a whole-assembly fashion,all the other blade rows are modelled as single passages.The unsteady computation starts by closing the nozzle at the back of the compressor,as well as exciting the blade in all modes of interest,which is the first flap(1F)and first torsion(1T)modes for the case studied here.Hence,in such computations,there are two sources of unsteadiness:the surge excitation and blade vibration.This approach allows the modelling of blade response,in addition to the unsteady forcing,during surge cycles,from which the flutter stability of the rotor blades can be determined.Figure 6 shows the comparison of mass flow and blade displacement time histories between the AU3D results and experimental measurements.It can be seen from Figure 6a that the 1T mode isinitially stable (during normaloperational conditions). As the compressor surges and R5 experiencesreversed flow,the 1T modebecomes unstable and the blade experiences flutter.However,during the recovery phase of the surge cycle,the blade becomes stable in the 1T mode again and the aerodamping becomes positive.It should be noted that the blade is highly unstable during the reversed flow period,and very high vibration amplitudes can be experienced especially for lower surge frequencies(i.e.bigger exit plenum volumes).The measured data,shown in Figure 6b,seems to show a similar trend.It is seen that the blade experiences very high vibration levels during certain periods of the surge cycle only,while amplitudes being low during other periods.The effects of surge loading,the so-called“hammer shock”,is also evident in the measured data.

Fig.6 (a)Time history of mass flow rate and blade displacement for the 1T/6ND mode;(b)Time history of measured blade displacement in experimental tests.
Overall,the results obtained using the hybrid fullannulus/single-passage model compare quite well with the results obtained using a single-passage mixing plane strategy.The single-passage mixing plane method for surge modelling offers good computational efficiency over an equivalent whole-annulus analysis,but it cannot model the rotating stall to surge transition.It is inherently assumed that the unsteadiness is axial during surge.However,the method can produce a first-order approximation to the blade loadings during surge and could be used to determine the axial gap between blade rows.This approach would be of more interest if the blade loadings were higher during the surge than the rotating stall that precedes it.Moreover,such an approach can be used for determining the weakest stage in a multistage core compressor.
4 Forced Response Due to Asymmetric Flow Features
The forced response of bladed discs is a very common vibration problem during the development phase of multi-stage compressors.A primary mechanism of blade failure is high-cycle fatigue(HCF)which is cause by vibrations at levels exceeding the material endurance limits.Two most common types of forced response vibration of core compressor are:
1.Rotor/stator interactions driven by blade passing,which usually occurs in relatively high engine orders.
2.Low engine order (LEO) forced response vibrations.
For the first type of forced response,traditional industrial practice is to identify possible resonances,at engine order(EO)frequency crossings,from the Campbell diagram and to try to avoid them by tuning the blade frequencies.The usefulness of this approach alone is however limited by the lack of knowledge of the resonant response levels.The actual blade response level is dependent on two quantities:unsteady aerodynamic loading and total damping in the mode of interest,both of which can be modelling using numerical computations.Therefore,there is a strong case for the development and use of advanced numerical tools for the prediction of absolute vibration levels of blades.Nevertheless,forced response methods for this type of interactions are well established.The second type of forced response,a less researched variant,arises when the unsteady aerodynamic forcing function contains low-order harmonics,hence the term LEO forced response.A typical example is stator/stator clocking in a core compressor.Such harmonics are due to some loss of symmetry in the flow which may be due to a general unsteadiness that persists throughout the engine.Similarly,blade-to-blade variations due to manufacturing tolerances,errors in controlling the variable stator vane angles,and“blocked”stator passages are known to generate low harmonics.
[1]conducted a computational forced response analysis for the first five blade rows of a civil aero-engine core compressor,hereafter labelled asS1(40),R1(31),S2(32),R2(38),andS3(50),where the number within brackets indicates the number of blades.Figure 7(a)outlines the geometry of the 5 blade rows in the core compressor.Interest was particularly paid to the forced response of the R2 blade row due to a blocked stator vane passage,i.e.stagger variation in one of the stator blades.This asymmetry feature in geometry may arise from manufacturing tolerances or, under extreme circumstances,due to a malfunction of the control mechanism for the variable stator vane.To investigate the effect of such feature on the forced response ofR2,computations were carried out with a gradual blockage by rotating one of the S2 blades by 10,20 and 25 degrees,an approach which links theR2response levels as a function of the blockage angle.

Fig.7 (a)The core-compressor geometry(left to right:S1,R1,S2,R2andS3);(b)Steady state Mach number contours atS2exit.
The steady state Mach number contours atS2exit for the 25°blockage case are plotted in Figure 7(b).It is seen that the effects of the blockage on the flow are confined to the blocked passage and to its immediate neighbours.The whirl angle variations arising from such a flow will cause low-engine-order harmonics which will excite the vibration modes of blade rowR2.Unsteady computations were subsequently carried out using the full-annulus 3-row (S2/R2/S3)modelto allow the travelling and developmentofflow disturbancesfromS2to the downstream domain.Maximum blade response for the bending and torsional blade mode was calculated from the modal force and aero-damping,and is plotted in Figure 8 for the assembly modes of interest as a function of stator blockage angle.It is seen that the response for Mode 1 is very high at 25 deg blockage,a feature that must be considered duly in the design process of a core compressor.
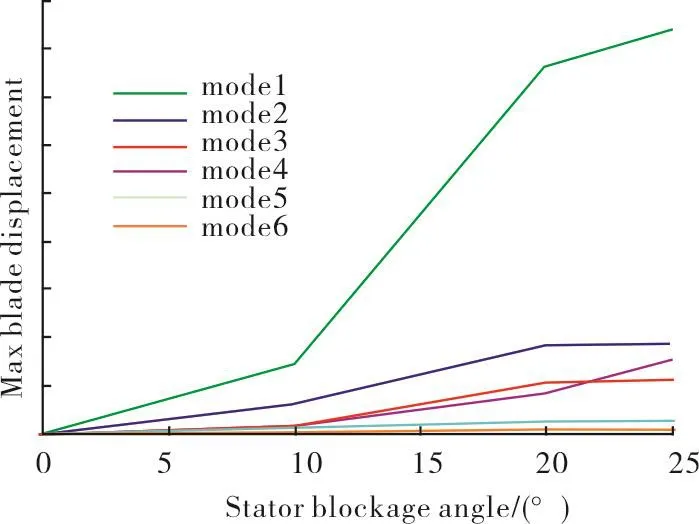
Fig.8 Maximum blade response for assembly modes of interest as a function of stator blockage angle.
5 Acoustic Reflection Driven Flutter
Flutter as a self-feeding aeroelastic instability presents one of the biggest challenges in modern aeroengine designs.This interaction between the unsteady aerodynamic loading and the blade motion can lead to the amplification of vibration levels resulting in high-cycle fatigue blade failures.Although there have been extensive studies about flutter stability of compressor or turbine blades,very limited work can be found regarding the effects of rotor-stator acoustic interaction on flutter stability of embedded blades.For an embedded rotor within a multi-stage compressor,flutter can occur when the acoustic pressure fields upstream and/or downstream of the blade row are cut-on(i.e.wave propagates without attenuation).Acoustic pressure waves generated by rotor vibration propagate between(and are reflected at)blade rows,influencing the flutter stability of the embedded rotor.As the use of blisks with very low mechanical damping is becoming more common in modern aeroengine designs,accurate prediction of flutter stability in a multi-row environment becomes vital in multi-stage compressor design.
The influence of acoustic reflections from adjacent blade rows on flutter stability of an embedded blade row wasinvestigated by reference[3-4].Thetestcase compressor features 9 highly loaded stages on a single spool contributing to an overall pressure ratio of 22:1.Titanium blisks were installed on the front stages for weight saving.The inlet guide vane(IGV)and first three stages of stator vanes(VSV)have adjustable blade stagger angle which operate with different settings according to spool speed.The domain used for steady and unsteady flutter computations are shown in Figure 9.The rotor row of concern(rotor2)which showed flutter instability in experimental tests has a hub/tip ratio around 0.7.In all the flutter computations presented,the blades were excited in first flap(1F)mode at a reduced frequency of 1.2.Results were shown for the peak efficiency operating point.At this condition,the inlet relative Mach number at tip is around 0.8 and the flow remains subsonic(apart from the suction peak)over the blade.For unsteady flutter computations,aerodynamic damping was computed from the logarithmic decrement ofthe displacementtime history.Unsteady flutter computations were performed for the isolated row,3 blade row and 5 blade row assemblies respectively(Figure9b). Identical operating conditions were maintained for all cases studied regardless of the number of blade rows used in the unsteady computational domain.Non-reflective boundary conditions were used to minimise numerical boundary reflection.Sensitivity of flutter stability of the embedded rotor is studied by comparing blade aerodynamic damping for different assemblies.

Fig.9 (a)Steady CFD domain;(b)The 9-stage high-pressure compressor with Titanium blisks for the front stage rotors;(c)Computational domain for flutter analysis.
Figure 10(a)shows the computed aerodynamic damping of rotor 2 for low nodal diameters-4 to 4.In this plot a positive ND represents a forward travelling wave(co-rotating with the rotor),and a negative ND represents a backward travelling wave(counter-rotating with the rotor).The aero-damping distribution of higher NDs are not shown since the blade becomes highly damped and thus does not pose a stability concern.As can be seen on the plot,the isolated rotor shows positive aero-damping for all NDs,suggesting that at the operating condition studied the rotor is always stable in the absence of other rows.With the introduction of upstream and downstream stators,aero-damping of the embedded rotor changes significantly from that of single blade row analysis.It is stressed again that,this is not due to the change of flow on rotor 2 as the numerical set up ensures that the base steady flow on rotor 2 is the same in all the computations.Positive,as well as negative effects on aero-damping can be observed from the plot.Moreover,the least damped mode shifts from 2ND(in single blade row analysis)to 0ND(in multi blade row analysis),and flutter is seen at 0ND with a small negative damping which is in accordance with experimental observations. The influence of adjacent blade rows on flutter stability of the embedded rotor is clearly seen based on this plot,where the stable isolated rotorbecomesunstable due to interaction between blade rows.This interaction between the blade rows is considered to be acoustic since the frequency of concern is well away from any engine order or forced response frequencies.
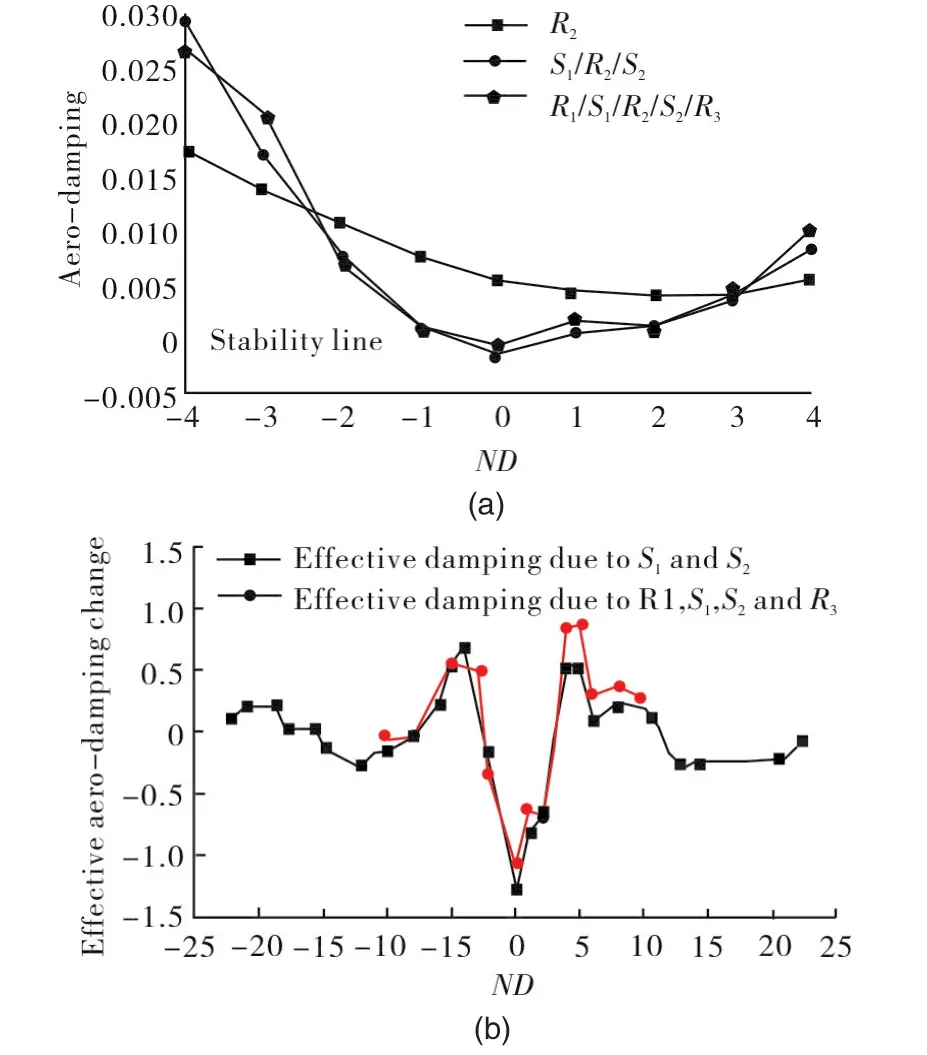
Fig.10 (a)Aero-damping forR2in different assemblies;(b)Change ofR2aero-damping due to the presence of adjacent blade rows.
In orderto understand theeffectofacoustic interaction from adjacent stators on different travelling modes,the differences in aerodynamic damping of the rotor between multi blade row assemblies(labelled asS1/R2/S2andR1/S1/R2/S1/R3respectively in Figure 10a)and isolated blade row(labelled asR2in Figure 10a)are computed and normalised by the‘blade-only’damping(aero-damping of isolatedR2),which are plotted in Figure 10(b).The‘effective aero-damping change’due to acoustic reflections represents the contribution of acoustic reflections to damping of the blade.This term provides a good measure of acoustic reflection effects.As can be seen in the plot,a cyclic distribution about the zero-stability line can be identified.Positive and negative effects(due to reflections)are clearly shown in this plot where the largest decrease in aero-damping is seen between-2ND and 2ND and the most increase in stability is seen in the vicinity of-5ND and 5ND.This influence of reflections on blade aerodynamic damping decreases for higher NDs as the acoustic modes cut-off,and the amplitude of the propagating pressure waves decay along the path of travel.Moreover,by comparing effective damping of the 3 blade row case and the 5 blade row case,it is obvious that R1 and R3 which are farther away have little influence on flutter stability ofR2.Therefore it is appropriate to assume that interactions from not immediately adjacent blade rows are negligible for this test case and,in order to reduce computational costs,those blade rows could potentially be discounted.
5 Conclusions
Extensive research has been conducted in the past decades to develop a predictive capability for multi-stage compressor aeroelastic stability,which can minimize rig and engine testing by means of advanced simulations that will cover the flight envelope in an efficient manner.This paper reviews some of the past work,and highlights some important findings and lessons learned that resulted from these investigations.
1)The variable-vane scheduling plays an important role in determination of the nature of rotating stall in multi-stage compressors.From a steady-state flow point of view,the mal-scheduling of variable-vanes results in a significant drop in flow,pressure ratio,and efficiency.In the case of the high-band rotating stall,the disturbances diffuse very rapidly downstream.Hence,only the blade row adjacent to rotating stall is likely to experience high response levels.From a design point of view,it is important to demonstrate that the compressor is free from rotating stall using a simple and cost-effective design tool.From a diagnostic point of view,it is important to understand rotating stall in terms of both the exact pattern and speed of the stall cells so that any critical vibration modes can be identified and avoided.
2)Using a single passage model of whole multistage compressor assembly,not only can one model steady flow near stall but one can model a simplified axial surge event using mixing planes and produce the hysteresis loop for compressor.The method allows a total flow reversal(negative mass flow)and recovery from it.From an engineering viewpoint,the simple method can be used to obtain a first-order approximation to surge loading.The approach can be of more practical use,e.g.,axial gap approximations,provided that the unsteadiness during surge is mainly axial and the loadings during surge are higher than the rotating stall that precedes it.Further studies using full-annulus blade row for the rotor of interest reveals a strong relationship between the flutter stability of the rotor and the transient mass flow,where the blade mode studied here is seen to be unstable during flow reversal periods of the surge,and subsequently regains stability as the compressor recovers.
3)An integrated aeroelasticity methodology,based on large-scale numerical modelling,has been described for full-annulus multi-bladerow forced analysis of core compressors.It was shown that partially blocked stator passages can cause large vibratory response.Although extremely unlikely,such eventualities need to be addressed at the design stage.Stator angle variations due to the difficulties of controlling all variable inlet guide vanes to the same level of accuracy,even though believed to have less impact than blocked passages,may also cause unexpected low engine order excitation.
4)The effect of blade row interactions on flutter stability of an embedded rotor was investigated using multi-row full annulus unsteady CFD computations.It was found that acoustic reflection has significant impact on flutter stability of an embedded rotor blade in a multistage compressor.As the use of blisks,which have very low mechanical damping,is becoming more common in modern aero-engine designs,effects due to acoustic reflection on aerodynamic damping should be taken into account during early development stages of an engine.Flutter computations were performed on an embedded rotor in a high-pressure compressor with and without the presence of its adjacent blade rows.Acoustic reflections from the two neighbouring stators shows positive and negative effects on aerodynamic damping of the embedded rotor for different NDs,whereas the effect of reflection from blade rows further away is found to be negligible in this case.
6 Acknowledgements
The authorthanks Rolls-Royce plc forboth sponsoring this work and allowing its publication.The authorgratefully acknowledges the contribution of colleagues who worked and who are currently working at the Vibration UTC Imperial College London and Rolls-Royce plc.
[1]M.Vahdati,A.I.Sayma and M.Imregun,G.Simpson,(2005).Multibladerow Forced Response Modeling in Axial-Flow Core Compressors.ASME.J.Turbomach,129(2):412-420.
[2]M.Vahdati,G.Simpson and M.Imregun,(2006).Unsteady,flow and aeroelasticity behaviour of aero-engine core compressors during rotating stall and surge.51st ASME Turbo Expo,Publisher:AMER SOC MECHANICAL ENGINEERS,Pages:153-163
[3]F.Zhao,J.Nipkau,M.Vahdati,(2015a).Influence of acoustic reflections on flutter stability of an embedded blade row.Proceedings of the Institution of Mechanical Engineers,Part A:Journal of Power and Energy,Vol 230,Issue 1,pp.29-43
[4]F.Zhao,J.Nipkau,M.Vahdati,(2015b).A Simple Low-Fidelity Model for Embedded Blade Row Flutter Prediction.ASME.TurboExpo:PowerforLand,Sea,and Air,Volume7B:Structures and Dynamics V07BT34A002.
[5]A.I.Sayma,M.Vahdati,L.Sbardella,and M.Imregun,(2000).Modeling of three- dimensional viscous compressible turbomachinery flows using unstructured hybrid grids.AIAA J.,38(6),pp.945-954.
[6]P.Spalart and S.Allmaras,(1992).A one-equation turbulence model for aerodynamic flows.Thirtieth Aerosp.Sci.Meet.Exhib.Aerospace Sciences Meetings,American Institute of Aeronautics andAstronautics,AIAAPaper No.92-0439.
[7]M.Vahdati,G.Simpson,and M.Imregun,(2011).Mechanisms for wide-chord fan blade flutter.J.Turbomach.,133(4),p.041029.
[8]M.Choi,N.H.S.Smith,and M.Vahdati,(2013).Validation of numerical simulation for rotating stall in a transonic fan.J.Turbomach.,135(2),p.021004.
[9]J.Dodds,and M.Vahdati,(2014).Rotating stall observations in a high-speed compressor part II:numerical study.J.Turbomach.137(5),p.051003.

