连续式风洞电机-联轴器-压缩机转子轴系横向振动分析∗

（中国空气动力研究与发展中心）

0 引言

连续式风洞的动力装置的主要作用是驱动实验气体介质以所需的马赫数在风洞内循环流动。动力系统轴系一般由压缩机转子、联轴器、电机转子、轴承等部件组成，具有转速范围广、单级压比高、轴系复杂集成等特点。整个旋转轴系是机组的核心部件之一，其动力学特性直接关系到整个机组的稳定安全运行[1-2]。在轴系设计时，需要建立详细准确的转子动力学模型，合理设置转子的临界转速区间，有效规避转子轴系的共振风险。对于柔性转子则必须进行不平衡响应分析，将轴系的振动值控制在合理的水平以内。

在轴系转子动力学计算方面，国内外学者进行了大量的研究。自从Jeffcott[3]使用集中质量模型计算转子的动力特性以来，在诸多学者的努力下，转子动力学理论已经日臻完善，在实践中也得到了越来越广泛的应用[4-7]。Lund[8]提出用8个刚度、阻尼系数表述轴承油膜力的线性化模型，并以此为基础研究了转子-轴承系统的稳定性问题。通过对Reynolds方程的简化，还可以得到其他理论模型来计算轴承油膜力[9-10]。白中祥[11]等使用ANSYS软件计算了支承的静刚度和动刚度，并分析了支承系统的刚度对其临界转速和稳态不平衡响应的影响。徐俊[12]在计算电机转子的临界转速时采用经验公式计算单边磁拉力的影响，取得了和实验数据比较吻合的结果。刘清[13]从电机气隙出发推导了径向不平衡磁拉力表达式，并得出磁拉力的线性部分使系统固有频率下降，非线性部分使主共振峰左偏量增大的结论。高洪涛[14]利用工程法计算了膜片联轴器的刚度，并以此为基础建立了转子的动力学模型，研究了联轴器不对中和不平衡动力学特性。这些研究都为本文提供了颇有价值的参考。

本文以某连续式跨声速风洞的轴流压缩机系统为研究对象，建立了电机转子-联轴器-压缩机转子的轴系动力学模型，综合考虑了轴承、联轴器、支撑、单边磁拉力等因素对转子动力学特性的影响情况，计算出轴系的临界转速、振型以及不平衡响应等结果，并和实验数据进行了对比分析。

1 转子动力学建模

1.1 总体参数

某连续式跨声速风洞的轴流压缩机由异步交流电机直接驱动。整个轴系由压缩机转子、联轴器、电机转子、轴承组成。轴系布置如图1所示，轴系的基本参数如表1所示。图中的弹簧表示轴承或联轴器，中心线上的黑色实心点表示集中质量（惯量），带直线的实心点表示不平衡量。

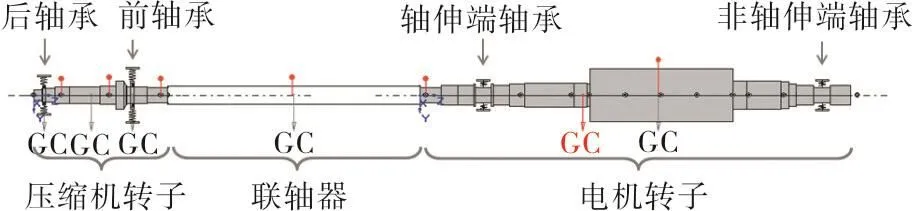
图1 轴系布置图Fig.1 Sketch of the shafting

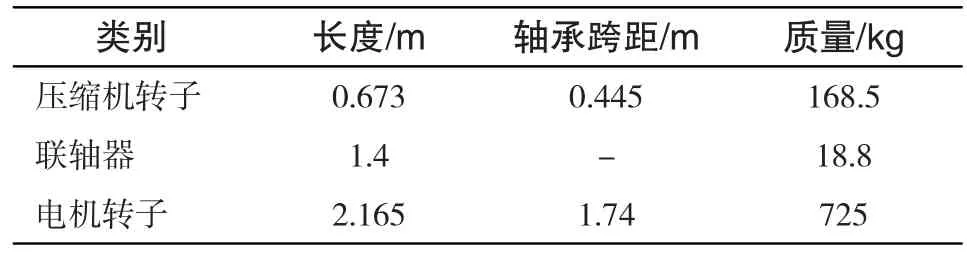
表1 轴系主要参数表Tab.1 Main parameters of the shafting

1.2 轴承

压缩机由径向滚动轴承和推力滚动轴承支撑，电机由两个径向滑动轴承支撑。本文使用式(1)所示的刚度和阻尼系数来表征滑动轴承的油膜力。由于滚动轴承的阻尼很小，可以忽略其影响。轴承的刚度和阻尼均是转速的非线性函数，在计算时使用表格形式的动刚度和动阻尼输入软件进行计算。轴承的刚度和阻尼特性见图2～图4所示。

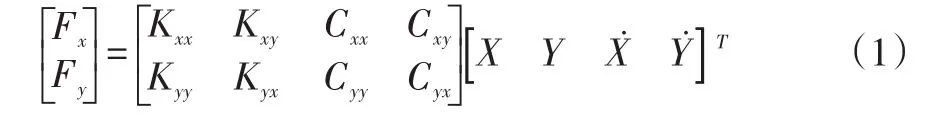
其中，Fx，Fy为油膜力在x，y方向的分量，Kxx，Kxy，Kyy，Kyx为刚度系数，Cxx，Cxy，Cyy，Cyx为阻尼系数，X，Y为轴颈涡动的位移在x，y方向的分量，Ẋ，Ẏ为轴颈涡动的速度在x，y方向的分量。

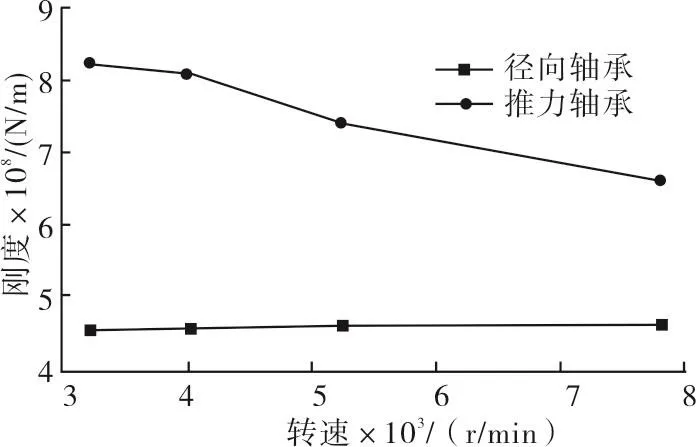
图2 压缩机滚动轴承刚度特性曲线Fig.2 Stiffness charateristic curve of the compressor rolling bearing

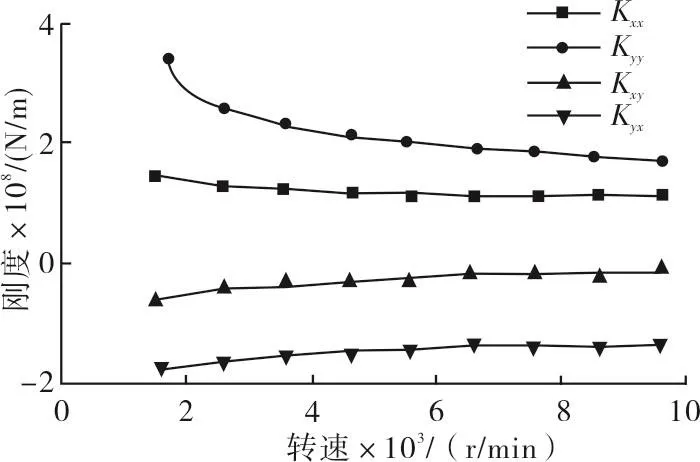
图3 电机滑动轴承刚度特性曲线Fig.3 Stiffness charateristic curve of the motor sliding bearing

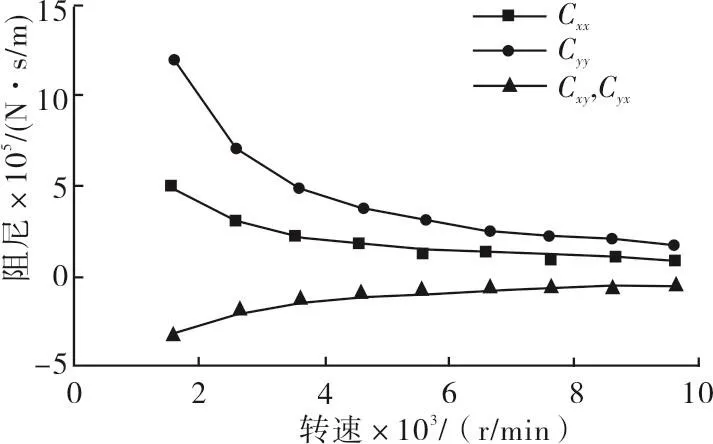
图4 电机滑动轴承阻尼特性曲线Fig.4 Damping charateristic curve of the motor sliding bearing

1.3 轮毂、连接环和叶片

如图5所示，压缩机主轴和轮毂设计成过渡配合。每一级轮毂的中间掏空，仅在两端和主轴接触。两级轮毂使用连接环螺接。一级轮毂的上游端面和主轴通过花键传递扭矩轴向通过锁紧螺母固定。因此，轮毂、连接环和叶片对压缩机主轴的横向弯曲刚度贡献很小，可以将轮毂、连接环以及叶片的质量和转动惯量集中分配到和主轴接触的部位。简单起见，不考虑轮毂和叶片的耦合振动。

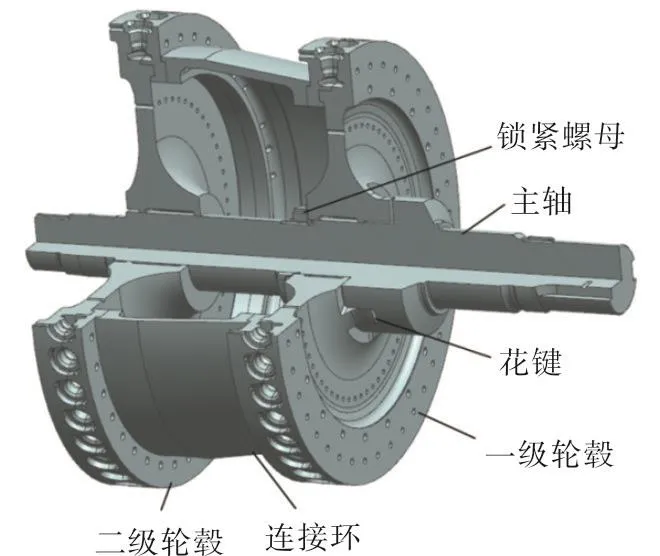
图5 轮毂和压缩机主轴的连接方式Fig.5 Connection of the hub and compressor shaft

1.4 联轴器

压缩机主轴和电机主轴间用弹性膜片式联轴器相连，联轴器包括一段长1.17m，单边壁厚仅2.3mm的薄壁中间轴。联轴器结构如图6所示。联轴器各方向的刚度值由供货商给出，如表2所示。

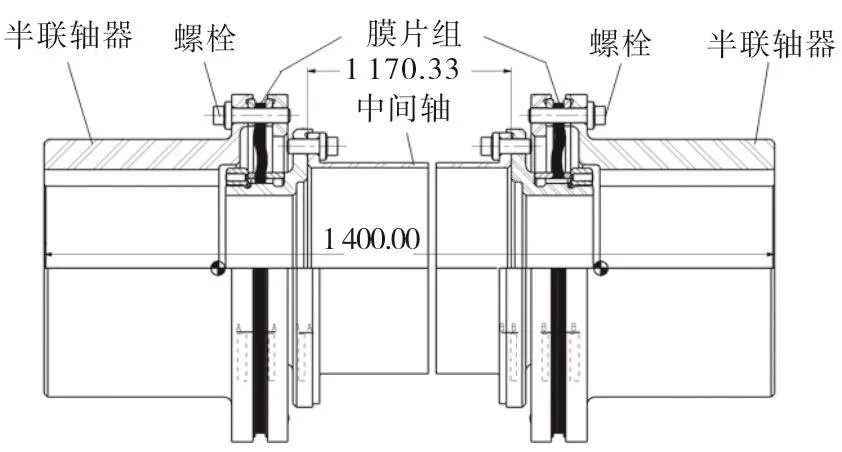
图6 联轴器结构图Fig.6 Structure of the coupling

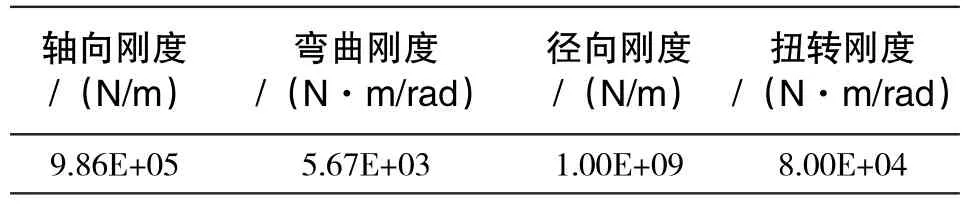
表2 联轴器刚度值Tab.2 Stiffness of the coupling

1.5 电机转子

如图7所示，电机转子为鼠笼型结构，铁芯由压装在电机主轴上的0.5mm厚硅钢片组成，转子绕组由插入铁芯槽中的铜质导条和环形的铜质端环组成。由于铁芯和主轴间的过盈量较大，铁芯对主轴的弯曲刚度有较大的贡献。根据设计经验，取等效刚度直径等于铁芯槽根部的直径比较合理。硅钢片的形状尺寸如图8所示，在计算中，铁芯段的电机主轴等效刚度直径取266.6mm。绕组和平衡盘的质量和转动惯量集中加载在电机相应的轴段上。

图7 电机转子结构Fig.7 Motor rotor structure

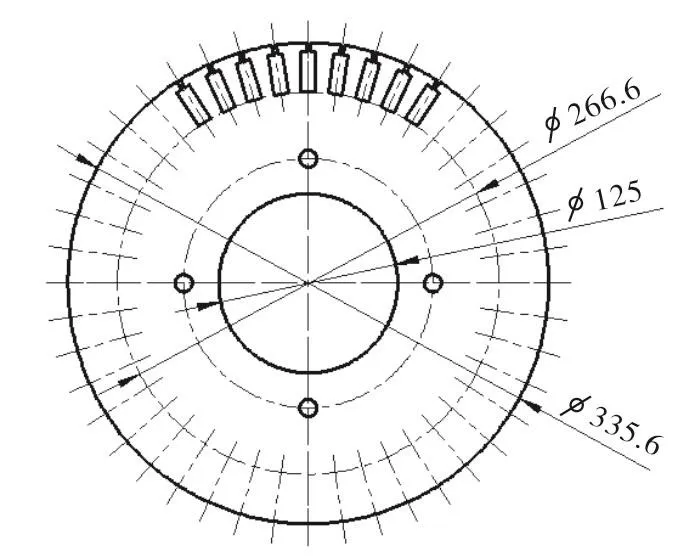
图8 硅钢片结构图Fig.8 Silicon steel sheet structure

受加工精度、装配精度、重力等因素的影响，电机定子和转子不可能完全同轴，二者之间的气隙值不均匀，从而导致电机转子受到偏向气隙较小一侧的单边磁拉力。该力相当于增加了转子的质量，降低了转子的弯曲刚度，最终使转子的临界转速降低。根据电机供应商推荐的经验公式(2)，计算单边磁拉力f。

式中，f为单边磁拉力，kg；D为转子外径，cm；L为铁芯长度，cm。

1.6 轴承支撑结构

在转子动力学计算中，如果轴承支撑刚度和轴承自身的刚度具有相当的量级，就必须考虑支撑刚度对转子的影响，否则会引入较大的误差。轴承支撑刚度可以通过实验进行测量，也可以使用有限元方法进行计算，本文采用后一种方法。

压缩机轴承的支撑结构如图9所示，压缩机的径向轴承座和推力轴承座通过法兰和压缩机整流体相连，整流体通过静叶和导流片焊接在压缩机壳体上，压缩机壳体的中心支撑在四个支座上，支座底部通过螺栓固定在基础平台上。

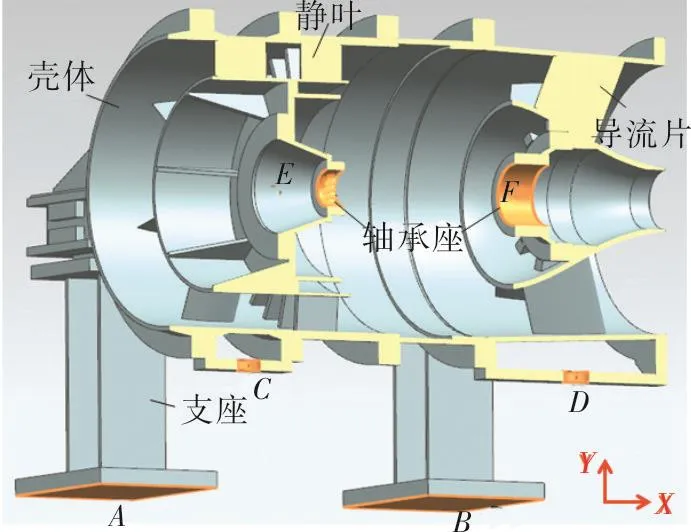
图9 压缩机轴承支撑结构剖面图Fig.9 Cross section of the compressor bearing supporting structure

建立有限元模型，所有连接面简化为绑定接触，约束机壳下方两个定位面A和B的径向位移。由于基础平台的刚度远大于压缩机壳体和支座，在计算时可以认为支座底面C和D完全固定。分别在径向轴承座E和推力轴承座F处施加一定的载荷，利用ANSYS静力分析模块计算支撑结构的静刚度，结果如表3所示。

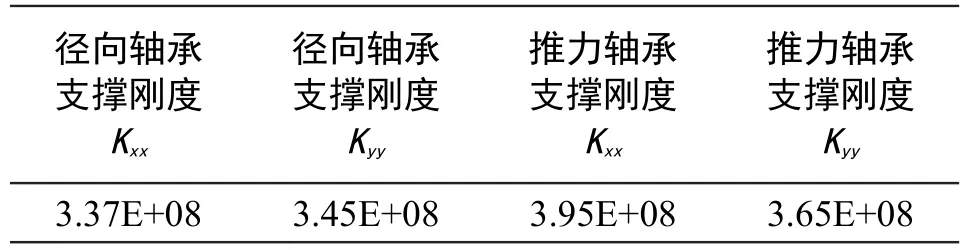
表3 压缩机轴承支撑刚度计算结果Tab.3 Calculation result of the compressor bearing support stiffness N/m

从计算结果可知，支撑结构的刚度甚至小于轴承本身的刚度，对整个转子的动力学特性影响较大，在轴系转子动力学计算中，必须将轴承支撑简化为各项同性的弹簧施加在转子模型中。这样组成的轴承-轴承座串联系统的等效刚度将小于轴承本身的刚度。

电机的两个轴承座刚度都远大于轴承本身的刚度，因此在计算中可以忽略电机轴承座的影响。

2 横向振动计算

在转子动力学计算软件DYNAMICS中，建立如图1的模型。考虑到本文第二节所述的各种因素对转子动力学计算的影响，计算出电机转子-联轴器-压缩机转子的轴系阻尼临界转速和振型。

计算结果显示，该轴系为典型的柔性轴系，一临界转速小于最大工作转速，轴系的一阶临界转速值计算结果如表4所示，和实验值的偏差在±5%以内，表明本文第二节对轴系各要素的简化分析是合理的，转子动力学计算结果具有较高的精确度。

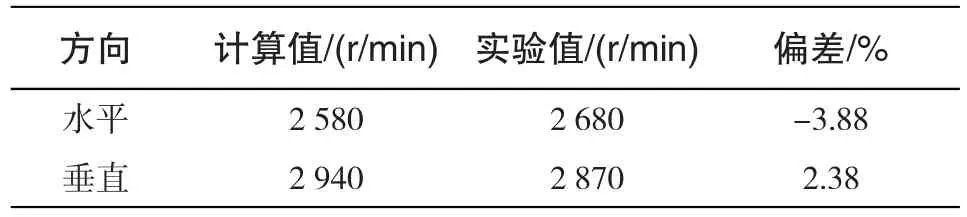
表4 轴系一临界转速计算值和实验值的对比Tab.4 Shafting 1stcritical speed comparation of the calculation and experiment result

轴系一临界转速对应的振型如图10所示，电机转子做弓形涡动，并通过联轴器和公共基础底座将振动传递给压缩机，带动压缩机转子做刚体位移。

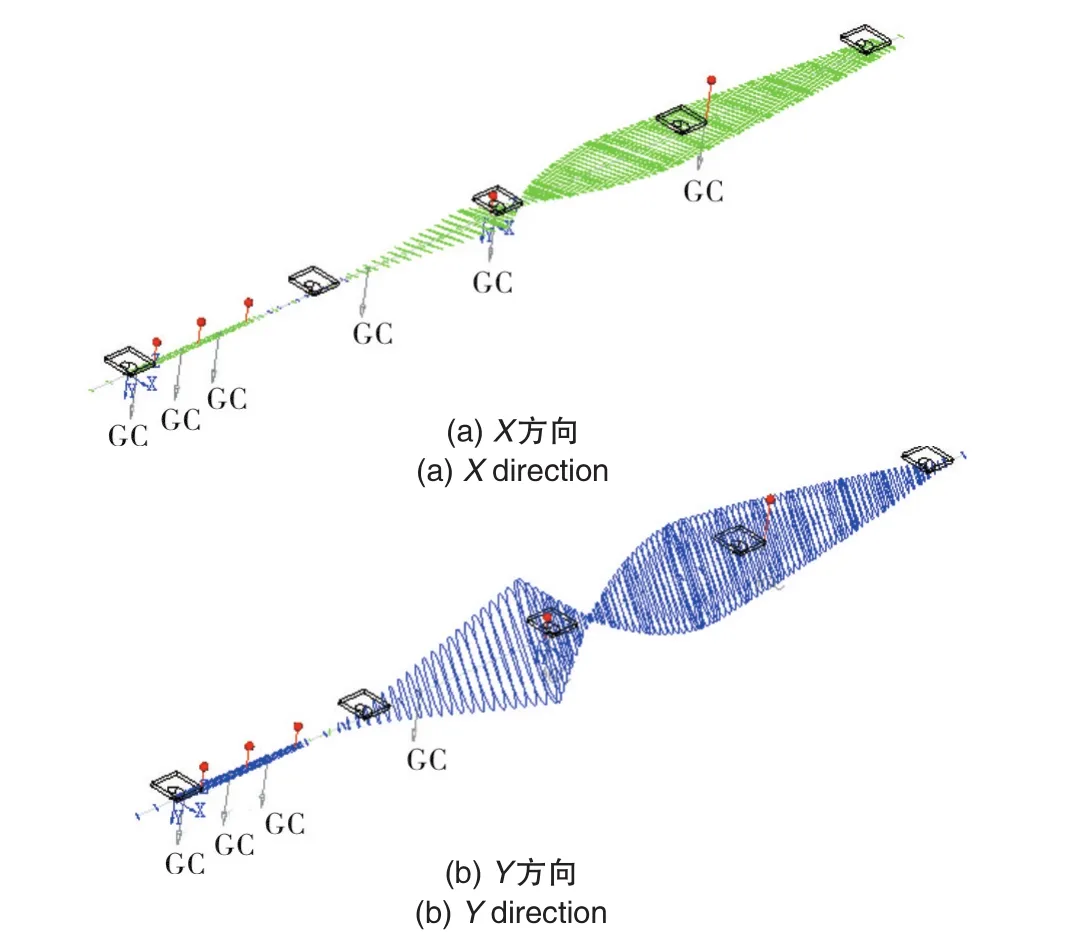
图10 轴系一阶振型Fig.10 Shafting 1stvibration mode

在电机转子和压缩机转子上施加不平衡量，计算轴系的不平衡响应，并归一化处理。以压缩机和电机轴承处（各轴承的位置分布如图1所示）的绝对振动为对象，对比分析计算值和实验测量值。结果如图11～图14所示。

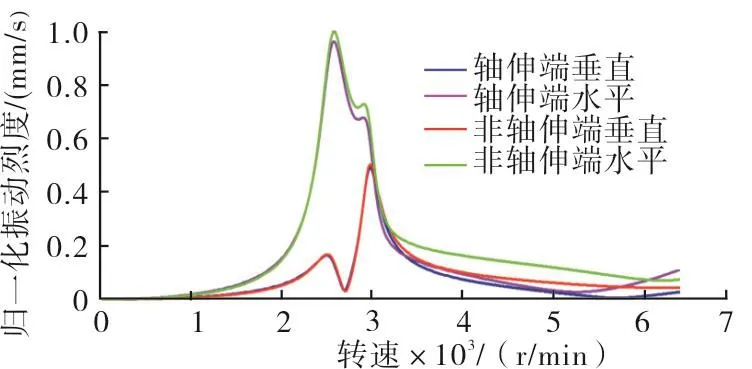
图11 电机轴承振动计算结果Fig.11 Calculation result of the motor bearing vibration

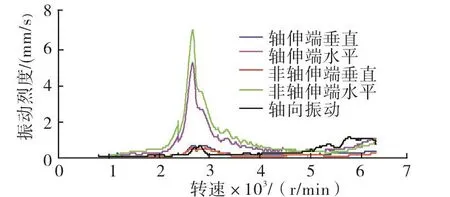
图12 电机轴承振动实验数据Fig.12 Experiment result of the motor bearing vibration

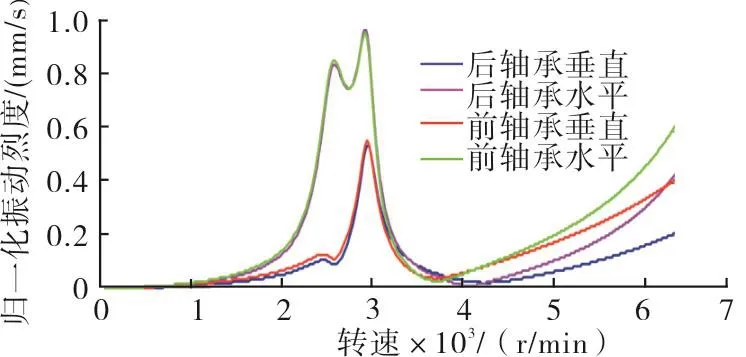
图13 压缩机轴承振动计算结果Fig.13 Calculation result of the compressor bearing vibration

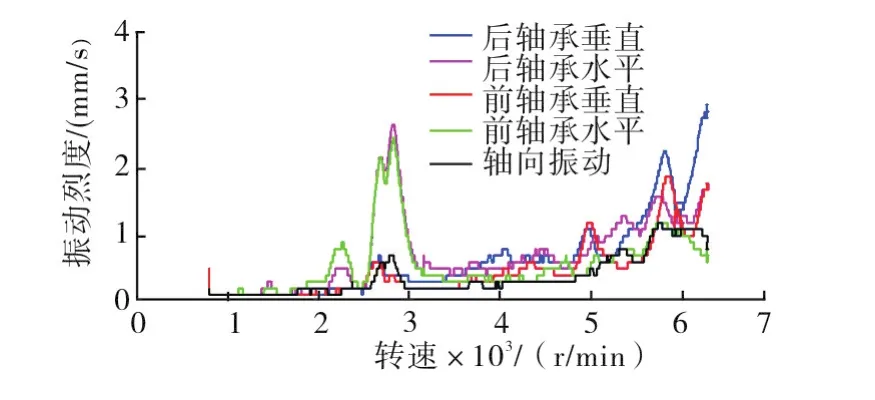
图14 压缩机轴承振动实验数据Fig.14 Experiment result of the compressor bearing vibration

3 结果分析

3.1 电机轴承振动分析

从图11的计算结果和图12的实验数据均可以看出，电机转子在经过一临界区间时，依次触发水平和垂直方向的共振。在交叉刚度的作用下，水平和垂直方向的振动相互耦合，一个方向的振动达到峰值时会导致另一个方向的振动也随之增大。在一临界区间，非轴伸端的振动略大于轴伸端振动，这和图10所示的结果相吻合。

经过一临界后，电机轴承水平和垂直方向的振动均快速下降。当转速升至5 500r/min以后，电机轴承振动再次抬升。这是由于压缩机转子开始逼近一临界，压缩机转子振动上升带动电机转子振动也随之升高。由于电机轴伸端和非轴伸端的滑动轴承具有较好的阻尼减振效果，可以有效衰减压缩机端传递过来的振动，因此在6 000r/min以上的高转速区间内，电机轴承振动值虽然有所升高，但是总体仍处于较低的水平。

3.2 压缩机轴承振动分析

压缩机转子本身的一临界转速高于7 000r/min，但是由于轴系的交叉耦合以及基础底座的振动传递作用，压缩机转子的振动会受到电机转子的影响。由于压缩机前轴承和后轴承均为滚动轴承，自身阻尼较小，对于电机转子端传递过来的振动衰减能力不足，因此在电机转子经过一临界时，压缩机轴承水平方向振动出现两个明显的尖峰，分别对应电机转子水平方向和垂直方向的共振。

从3 000r/min以后，压缩机转子振动明显下降，到5 000r/min以后又逐渐上升。这是因为压缩机转子本身开始逼近一临界，由于压缩机轴承阻尼较小，对共振的衰减能力不足，因此两个方向的振动均明显上升。

此外，可以注意到。图13的计算结果和图14的实验数据存在一定的偏差。主要体现在2 900r/min左右的垂直方向振幅和6 000r/min以上的垂直方向振幅。这主要是因为压缩机轴承座和基础在垂直方向的动阻尼与计算值有所差距导致的。

4 结论

1）本文基于DYNAMICS软件建立的压缩机转子-联轴器-电机转子轴系模型，考虑到轴承动刚度和动阻尼、支撑刚度、电机磁拉力等因素，计算得到轴系的临界转速和实验数据的误差小于±5%，不平衡响应和实验数据吻合度较好，表明本文建立的模型精度较高，计算结果可信。

2）电机为典型的柔性转子，由于水平和垂直方向的刚度的差异，临界转速也不相等。水平振动和垂直振动在交叉刚度的作用下相互耦合，临界转速有分叉现象。

3）压缩机转子和电机转子之间的膜片联轴器具有一定的隔振作用，但是由于支座和基础的耦合作用，电机转子和压缩机转子的振动会相互影响。由于压缩机支撑在滚动轴承上，阻尼较小，因此，它受到电机端的影响也更为明显。

[1]廖达雄,黄知龙,陈振华,等.大型低温高雷诺数风洞及其关键技术综述[J].实验流体力学,2014,28(2):1-6,20.

[2]周恩民,程松,刘恺,等.0.6m连续式风洞压缩机系统的调试研究[J].流体机械,2015,43(11):10-15.

[3]Jeffcott H.H.The Lateral Vibration of Loaded Shafts in the Neighborhood of a Whirling Speed[J].Philosophical Magzine,1919,7(6):304-314.

[4]王维民,宋慧斌,陈立芳,等.离心式压缩机振动阻尼设计、辨识理论与方法发展综述[J].风机技术,2015(6):63-75.

[5]王正.转动机械的转子动力学设计[M].北京:清华大学出版社,2015.

[6]Ishida Y.,Yamamoto T.Linear and nonlinear rotordynamics[M].Weinheim:Wiley,2012.

[7]Chen W.J.Rotordynamics and Bearing Design of Turbochargers[J].Mechanical System and Signal Processing,2012,29:77-89.

[8]Lund J.W.,Thomsen K.K.A Calculation Method and Data for the Dynamic Coeffiecients of Oil-Lubricated Journal Bearings[C].Design Engineering Conference on Fluid Film Bearing and Rotor Bearing System Design and Optimization,Chicago:ASME,1978:1-28.

[9]成玫.转子-轴承-密封系统动力学特性研究[D].上海:上海交通大学,2009.

[10]Xiao Zhonghui,WangLiping,Zheng Tiesheng.An Efficient Algorithm for Fluid Force and its Jacobian Matrix in Journal Bearing[J].ASME J.of Tribology,2006,128(2):291-295.

[11]白中祥,吴伟亮,刘闳钊.支承系统的刚度对转子动力特性的影响[J].机械设计与研究,2012,28(4):18-21.

[12]徐俊.临界转速计算及其在电动机转子设计中的应用[M].上海:上海交通大学,2010.

[13]刘清,李琨,王肖锋,等.不平衡磁拉力作用下电机柔性转子非线性振动研究[J].中国机械工程,2014,25(18):2446-2550.

[14]高洪涛.膜片联轴器耦合的不对中转子-轴承系统动力学研究[M].西安:西安科技大学,2003.