基于谐响应分析的水环境下核主泵叶轮动应力研究∗
何 曦 徐胜利 刘海涛 王晓放 陈旭东
(1.大连理工大学能源与动力学院;2.南洋理工大学计算机科学与工程学院)
0 引言
核主泵叶轮是为冷却剂输送提供动力并将热量排出的设备,是核电站一回路压力边界组成部分。叶轮是核主泵内高速转动部件,同时作为核主泵的核心部件关系到核主泵运行的完整性,要求在高温、高压、强辐射环境下长期、安全、可靠地运行,直接影响冷却剂的输送,进而影响整个反应堆系统的安全。叶轮强度分析的关键因素包括叶轮模态分析、叶轮受到水压力脉动载荷特性、叶轮共振校核和振动响应分析。
核主泵叶轮在水中的模态参数与空气中模态参数不同。由于周围水附加质量的影响,在水中的模态频率比空气中的频率要低。孔铭等对叶轮干湿模态进行了实验研究,分析对比了叶轮干湿模态频率,得到由于附粘水的影响,每阶湿模态频率低于相应干模态频率的结论[1]。张新等基于叶轮水中流固耦合对轴流泵叶轮进行了模态分析,分析了叶轮在水中以及空气中的各阶频率以及振型,研究发现各阶固有频率下降系数范围在0.1~0.38,下降系数与各阶振型有关[2]。Liang[3]等讨论了附加质量对于模态的影响。郑小波[2]等采用Subspace以及Block Lancos方法求解了空气中模态,并且利用流固耦合求解了水中模态,而且对频率、振型等模态参数进行了对比。张学荣[5]等通过对叶片干湿模态有限元分析,比较了GE公司的水中频率下降率修正系数与实际每阶模态频率下降率。
叶轮在水环境下受到的阻尼比可以分为两部分,材料阻尼比以及流体介质阻尼比。Lazan[6]通过大量实验,总结了材料阻尼耗能与应力幅值的关系。Rao[7]等对叶片的阻尼比进行了讨论分析,而且提出了一种计算等效粘性阻尼比的方法。李鹏飞等提出了材料阻尼比的识别方法与计算公式,并对Kelvin模型进行了相应的修正[8]。
吴俊男等研究了某离心叶轮的材料阻尼比与气动阻尼比,并且给出了离心式叶轮的总阻尼比的非线性模型[9]。
叶轮在实际工作时,由于流场的不均匀,会受到流场施加的压力脉动[10-11]。由于扰动,从而导致振动等一系列问题,影响到整体结构的安全性。Chiang[12]研究了叶片受压力脉动作用的响应。Yao[13]等研究了双吸泵的压力脉动时域特性。Tanaka[14]等研究了高水头泵的振动特性以及动应力,同时Rao[15]等研究了汽轮机末级叶片的动应力的计算。Xu[16]等研究了基于拟静力的核主泵叶轮动应力分析方法,分析了缩尺模型叶轮在压力脉动荷载作用下的动力学响应,但是没有考虑压力荷载的相位分布,只考虑了压力荷载的大小,并且是通过拟静力分析来求解动响应,因此动力学分析存在一定的误差。
本文首先对真机叶轮进行了模态分析,得到叶轮湿模态参数,通过扇区模型与整体模型的对比,验证了整体模型计算可靠性。并且比较了干湿模态固有频率。通过流固耦合分析,计算了流体介质阻尼耗功,得到了流体介质阻尼比以及材料阻尼比,并且分析了流体介质阻尼比与材料阻尼比随着振幅变化关系。然后对叶轮压力脉动进行分析,对比了缩尺模型试验与数值模拟水力性能,研究了压力荷载时域、频域信息,并且分析了压力荷载幅值、相位的分布。最后通过叶轮干涉图分析,找出共振区域,通过水中谐响应分析,校核了叶轮共振,较为准确的分析了叶轮动应力。
1 CAP1400叶轮湿模态分析与阻尼比分析
叶轮的模态分为干模态与湿模态。干模态是指叶轮在空气中的模态,湿模态是叶轮在水中模态。由于水的附加质量的影响,湿模态特性与干模态特性相比,有显著的差别,比如频率等模态参数。而叶轮实际工作在水环境中,为了研究实际运行工况时的振动,需要考虑叶轮湿模态特性。空气中与水环境中的固有频率可以用式(1)、(2)表示。
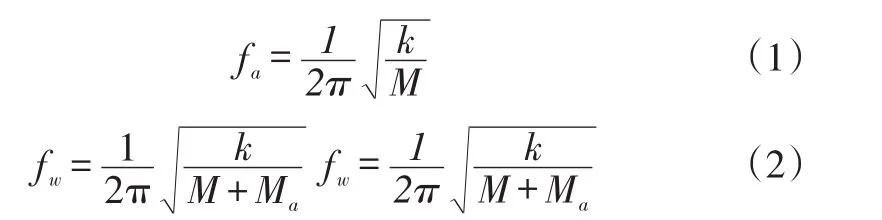
式中,fa,fw分别表示在空气中、水环境中的固有频率;k表示模态刚度;M为模态质量;Ma为附加质量。可以看出,由于水的附加质量的影响,在水中的模态频率比在空气中的低。湿模态的基本思想是以结构动力学方程为求解对象,为了体现流体对结构的影响,动力学计算时候,把流体的附加质量加到结构的质量阵上。如式(3)所示。
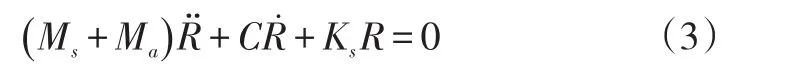
式中,Ms为结构的质量矩阵;Ma为流体的附加质量矩阵;C为阻尼矩阵;R̈,Ṙ以及R分别为结构的加速度矢量、速度矢量以及位移矢量。
1.1 CAP1400叶轮湿模态分析
为了校核核主泵叶轮动力学响应,首先需要对叶轮进行湿模态分析。叶轮材料参数如表1所示。

表1 叶轮材料属性Tab.1 Properties of the impeller material
叶轮湿模态计算模型如图1所示。叶轮模型采用ANSYS中SOLID187单元、水域采用FLUID221单元。
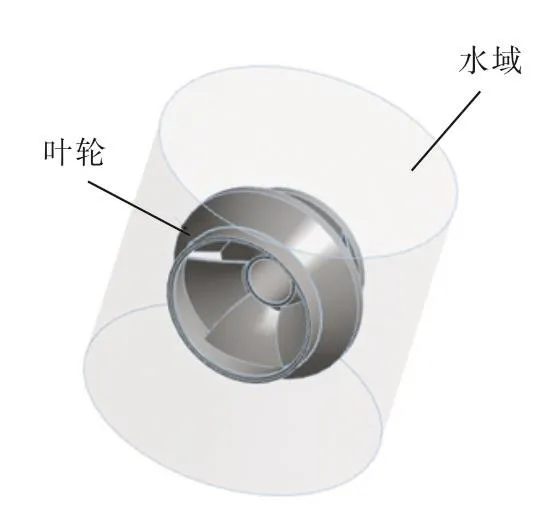
图1 数值模拟模型Fig.1 Numerical simulation model
对于循环对称模型,为了保证结果的准确性,常采用扇区模型进行计算。叶轮湿模态需要考虑叶轮与流体之间的耦合作用,模态提取方法为非对称提取,因此叶轮湿模态计算采用叶轮整体模型。为了验证整体模型的准确性,对比扇区与整体模型模态计算结果。图2为扇区结构与整体结构干模态固有频率对比结果。从图2中可以看出,整体结构与扇区结构固有频率结果差别不大。0节径下,两者误差为0.37%,1节径下,误差为0.37%,2节径下误差为0.21%。因此,采用整体结构计算叶轮模态是可行的。图3为叶轮各阶干湿模态频率。从图3中可以看出,每节径下,叶轮湿模态频率比干模态频率要低,并且不同节径,频率的下降率不同。0节径下,频率下降率为11.1%,1节径下,频率下降率为3.8%,2节径下,频率下降率为16.1%。
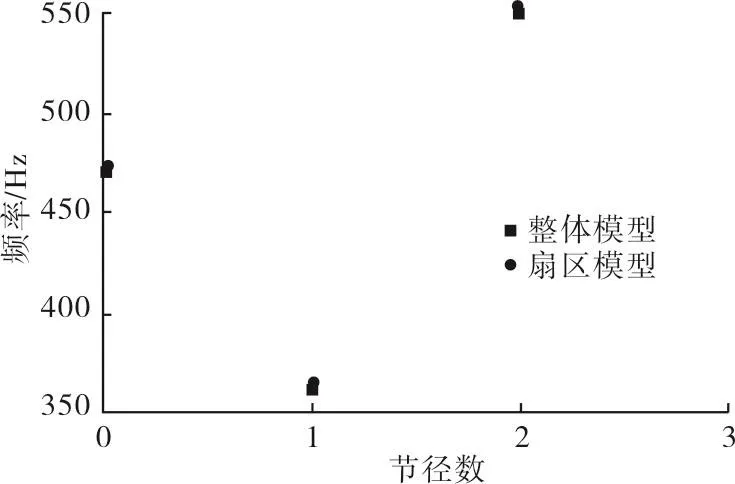
图2 扇区结构与整体结构固有频率对比Fig.2 Comparison of natural frequency of sector structure and overall structure
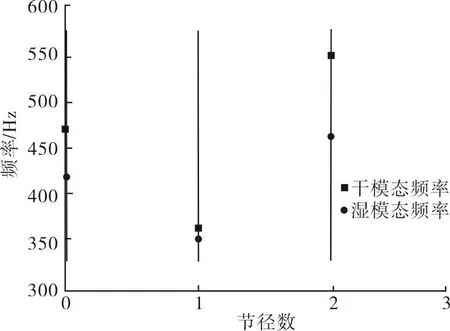
图3 叶轮干湿模态固有频率Fig.3 Air and wet modal natural frequency of impeller
1.2 CAP1400叶轮阻尼比分析
叶轮阻尼比对叶轮动力学特性有一定影响,为了精确研究叶轮动力学特性,需要计算出叶轮阻尼比。核主泵叶轮的阻尼比分为材料阻尼比与流体介质阻尼比。通过模态分析,根据公式(4)、(5)材料阻尼比可以计算出来。
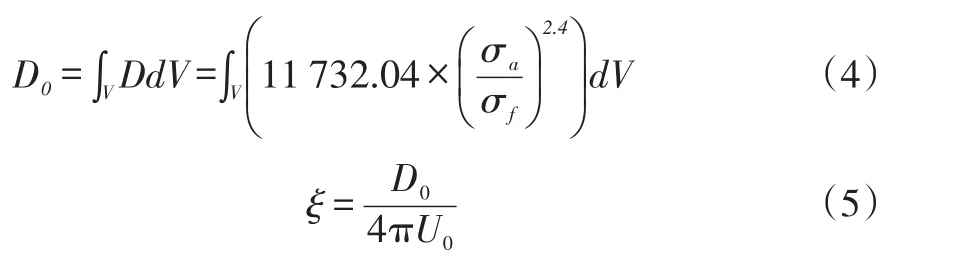
式中,D0为材料阻尼耗功;σa为应力幅值;σf为疲劳极限;U0为模态应变能。
图4为材料阻尼比随着振幅的变化曲线,可以看出,材料阻尼比随着振幅变化而变化,而且为非线性变化关系。
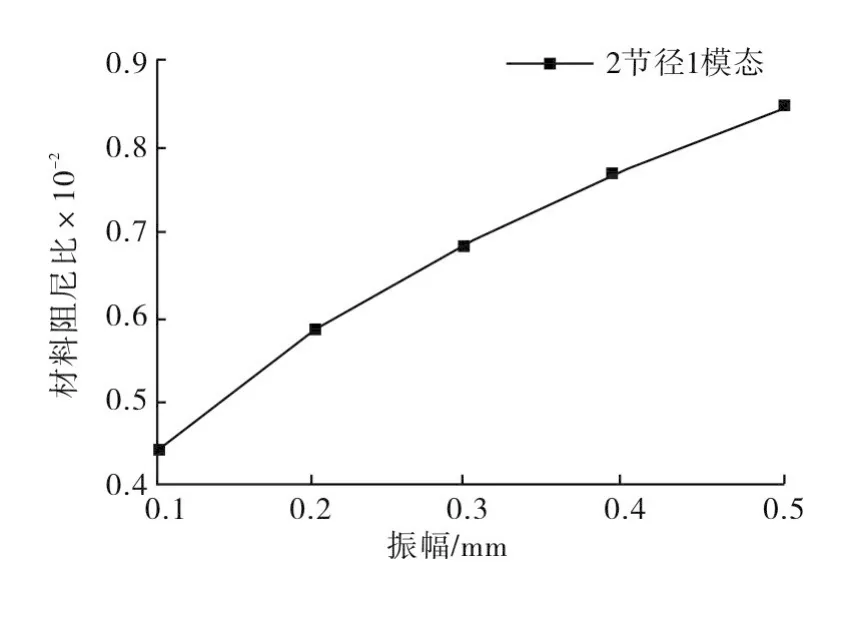
图4 材料阻尼比随着振幅变化曲线Fig.4 Material damping ratio with different amplitude
叶轮振动时,流体耗功,消耗了能量。这部分由于流体耗功产生的阻尼比为流体介质阻尼比。流体介质阻尼比计算公式为(6)、(7)、(8)。计算流体介质阻尼比最关键的部分是计算流体介质阻尼比耗功。而流体介质耗功可以通过流体与固体的耦合计算得出。
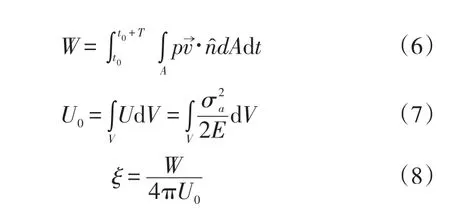
式中,W为材料阻尼耗功;p为压力;⇀为速度;̂为单位法向量;A为面积;t为时间;σa为应力幅值;E为弹性模量。
模态振型作为振动边界条件,通过流固耦合计算,求出流体介质阻尼耗功,通过公式(6)、(7)、(8)得出叶轮流体介质阻尼比。图5为流固耦合计算模型。
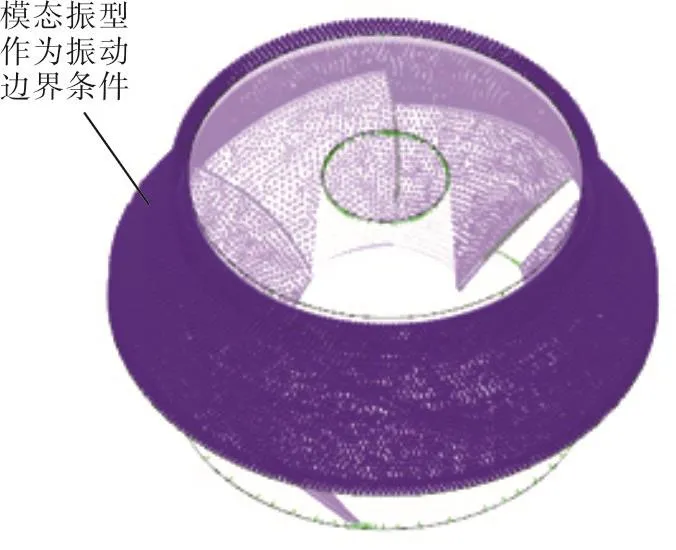
图5 流固耦合计算模型Fig.5 Fluid-solid interaction calculation model
从图6可以看出,同一模态下,流体介质阻尼比基本不随着振幅变化而变化。比较图4与图6可以看出,同一模态下,流体介质阻尼比比材料阻尼比大一个数量级,因此计算总阻尼比时可以忽略材料阻尼比影响。
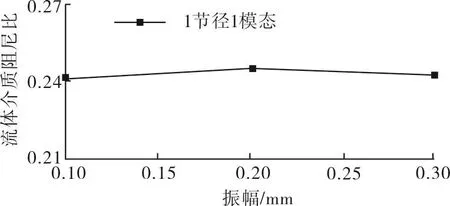
图6 流体介质阻尼比随着振幅变化曲线Fig.6 Hydrodynamic damping ratio with different amplitude
2 CAP1400叶轮压力荷载分析
叶轮在实际运行中,由于动静干涉以及流场不均匀性会产生一定的压力脉动。为了分析叶轮水中动应力,需要对叶轮所受到的压力脉动进行分析。图7为叶轮非定常计算流体域模型。首先分析缩尺叶轮模型非定常计算,并且与试验进行对比,表2为缩尺模型试验与数值模拟水力性能对比,其中流量误差为1.8%,扬程误差为1.8%,效率误差为2.8%,误差均在要求范围内,验证了计算平台的可靠性。然后分析真机叶轮流场特性,表3为真机叶轮流场计算边界条件。
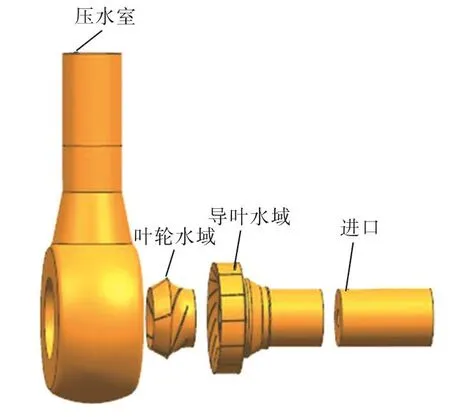
图7 叶轮CFD计算模型Fig.7 Impeller channel model for CFD calculation
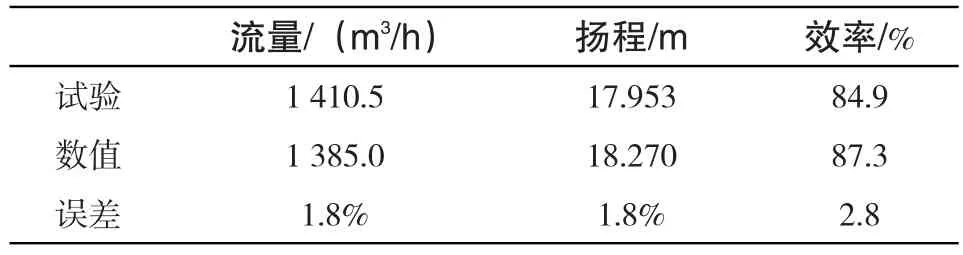
表2 缩尺模型试验与数值模拟水力性能对比Tab.2 The boundary condition of C flow field
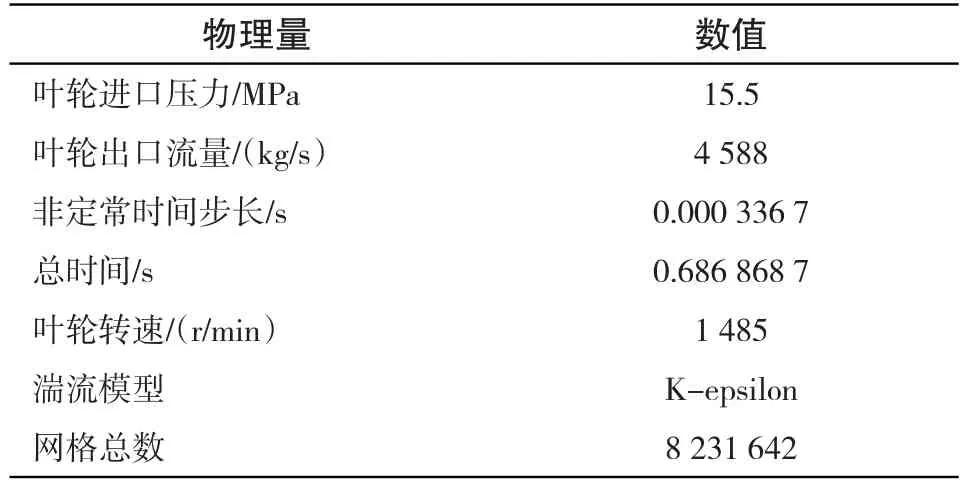
表3 CAP1400叶轮流场计算边界条件Tab.3 The boundary condition of CAP1 400 impeller flow field
由于非定常性以及动静干涉等原因,叶轮内部压力分布较为不均匀。图8为叶片前缘、尾缘点的压力脉动在两个周期内的时域图,图9为叶片前缘、尾缘点的压力脉动频域图。从图8可以看出,相比于叶片前缘,叶片尾缘的压力脉动的峰值较多。这是因为在叶片尾缘处,由于叶轮与导叶之间的动静干涉,造成了一个高频的脉动,并且频率大小与导叶个数有关。在本文中,导叶数为13,因此这个高频脉动的频率为13倍转频。从图9中可以很清晰看出,由于尾缘靠近导叶,在尾缘处压力脉动频域图中会出现一个较高的13倍转频的压力峰值。而叶片前缘由于与导叶相隔较远,13倍转频的压力幅值相应较小。
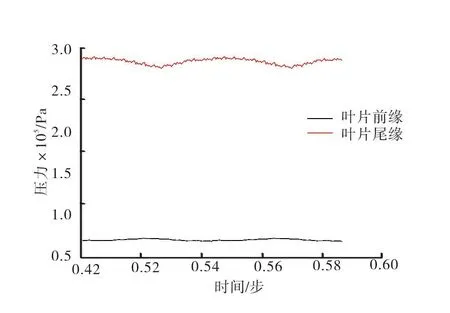
图8 叶片前缘与尾缘压力脉动时域图Fig.8 Pressure fluctuation time-domain diagram of blade leading edge and blade trailing edge
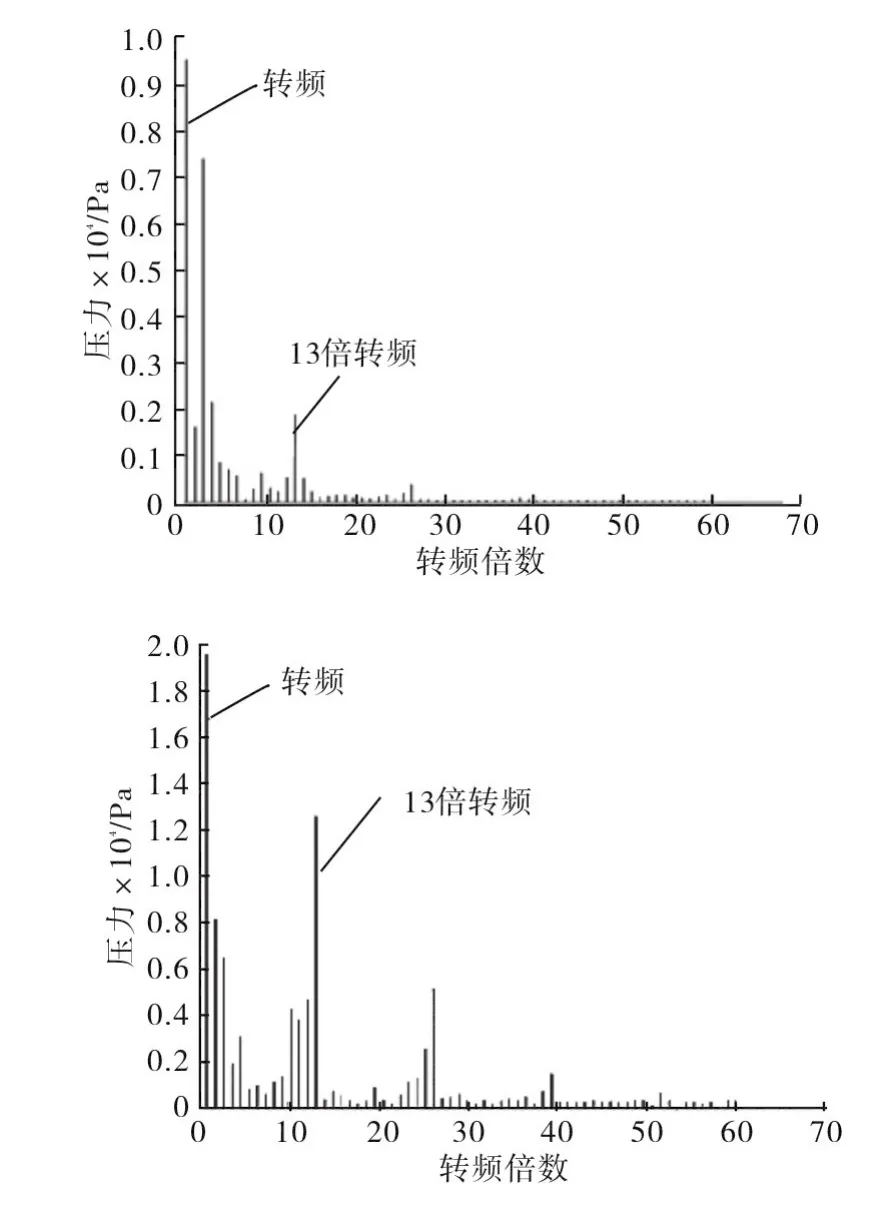
图9 叶片前缘(a)尾缘(b)压力脉动频域图Fig.9 Pressure fluctuation frequency-domain diagram of blade leading edge(a)and trailing edge(b)
叶片压力荷载在叶片不同位置的幅值与相位角均不相同,图10为叶片压力荷载在1节径频率下叶片压力面的幅值与相位分布图。图11为叶片压力荷载在1节径频率下叶片吸力面的幅值与相位分布图。可以看出,叶片不同位置的压力脉动幅值不同,叶片压力面幅值大于吸力面幅值。同样的,在叶片不同位置,压力脉动相位也是不一样的,存在着相位差。因此,为了准确计算压力荷载对叶轮动力学特性影响,需要考虑叶片不同位置压力荷载的幅值与相位。
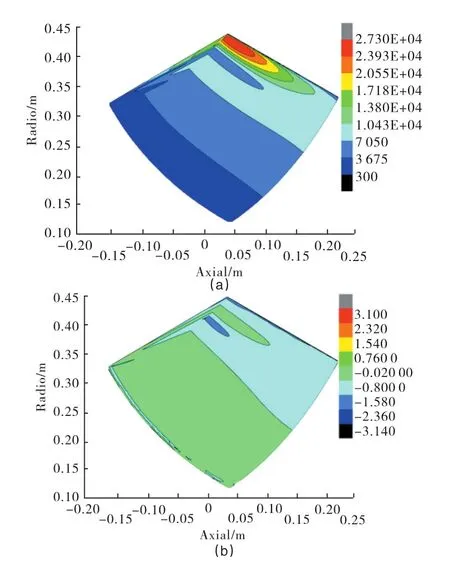
图10 1节径1模态固有频率下叶片压力面压力幅值、相位分布Fig.10 Blade pressure amplitude(a)and phase distribution(b)of pressure side in 1-ND first mode frequency
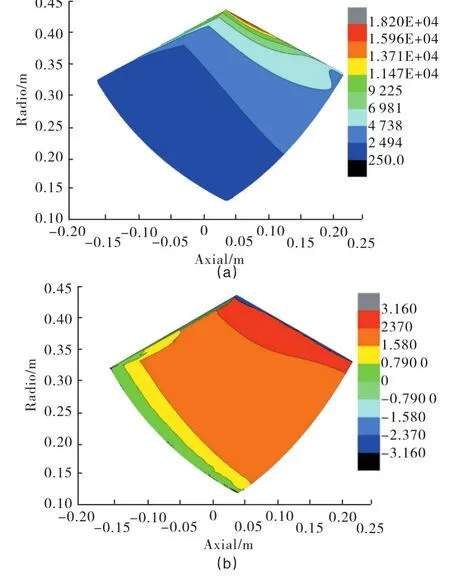
图11 1节径1模态固有频率下叶片吸力面压力幅值(a)相位(b)分布Fig.11 Blade pressure amplitude(a)and phase(b)distribution of suction side in 1-ND first mode frequency
3 CAP1400叶轮谐响应分析与共振校核
通过分析叶轮湿模态、阻尼比以及压力荷载,得到求解叶轮动应力时需要的输入量。图12为叶轮谐响应分析流程图。
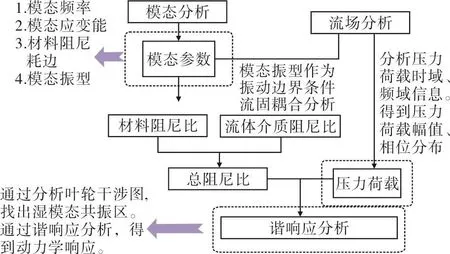
图12 谐响应分析流程图Fig.12 Harmonic response analysis process
核主泵叶轮工作在液体环境中,对叶轮进行动力学分析(谐响应分析)需要考虑周围流体介质的影响。为了校核叶轮强度,需要对叶轮进行共振校核。图13为叶轮干涉图。从图中可以看出,叶轮在1节径1模态下固有频率与激振力频率接近,因此,需要进行1节径1模态共振分析。
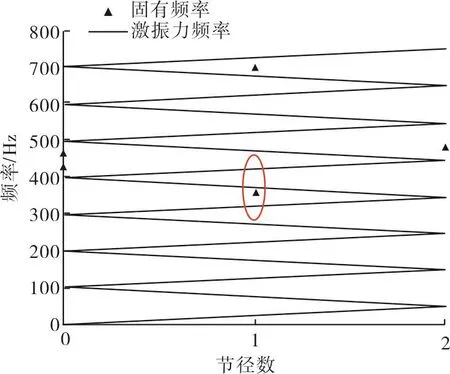
图13 叶轮干涉图Fig.13 Interference diagram of impeller
叶轮所受到的荷载为流场中的压力荷载,通过流体域节点与固体域节点的信息传递,将此前分析的压力荷载幅值以及相位信息施加到固体相应位置。图14为叶片流体域节点与固体域节点分布图。
对叶轮进行谐响应分析时,需要考虑周围液体环境的影响。设置水域中叶轮表面为流固耦合交界面,同时设置自由表面,刚性壁面。图15为流体域节点以及流固耦合交界面示意图,红色部分的流体域节点为流固耦合交界面,此处的单元是将流体与固体联系在一起的单元,是结构至流体的过渡。通过谐响应分析,得到了1节径1模态叶轮共振动力学响应。

图14 叶片流体域节点与固体域节点分布Fig.14 Blade fluid domain nodes and solid domain nodes distribution
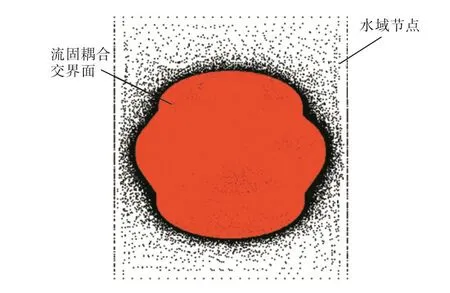
图15 流体域节点与流固耦合交界面Fig.15 Fluid domain nodes and fluid-solid interaction interfaces
图16为叶轮位移分布图与动应力分布图,可以看出,在受到流场中压力脉动荷载作用下,叶轮1节径1模态共振时,最大动应力为2.02MPa,并且最大应力点出现在叶根部分。
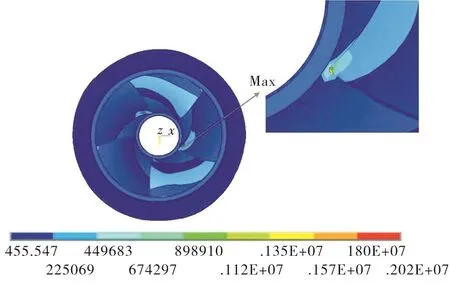
图16 叶轮1节径1模态共振等效应力云图Fig.16 Equivalent stress of impeller in 1-ND first mode resonance
4 结论
本文通过比较扇区模型与整体模型的模态频率,验证了整体模型的准确性。通过模态分析,比较了干湿模态频率。发现叶轮湿模态频率比干模态频率低,并且每阶模态下,频率下降率不同。通过模态分析,根据材料阻尼比计算公式计算出材料阻尼比。同时,通过流固耦合分析,计算出叶轮流体介质阻尼比。对比材料阻尼比与流体介质阻尼比发现,材料阻尼比比流体介质阻尼比小一个数量级,可以忽略材料阻尼比的影响。
然后分析叶轮流场,首先对比了缩尺叶轮模型试验与数值模拟水力性能,两者扬程误差为1.8%,效率误差为2.8%。并研究了叶轮所受到的压力荷载。分析叶片前缘与尾缘的压力脉动时域图、频域图发现,由于动静干涉的影响,尾缘处13倍转频的压力幅值较大。而且在叶片不同位置,压力荷载的幅值与相位均不相同。在研究叶轮动应力时,需考虑压力荷载的幅值与相位。
最后通过分析叶轮干涉图发现,叶轮1节径1模态处固有频率与激振力频率接近,因此校核了1节径1模态共振。通过流体节点与固体节点的耦合,将压力荷载信息传递到固体对应位置。通过水中叶轮谐响应分析,得到了在1节径1模态共振下的叶轮动应力分布,研究发现,最大动应力为2.02MPa,并且出现在叶根部分。
[1]孔铭.核主泵叶轮干湿模态的实验探究[D].大连理工大学,2014.
[2]张新,郑源,钱钧,等.基于流固耦合的卧式轴流泵叶轮模态分析[J].水电能源科学,2015(7):164-167.
[3]Liang Q W,Rodríguez C G,Egusquiza E,et al.Modal Response of Hydraulic Turbine Runners[C]//International Association of Hydra Engineering&Research,Symposium on Hydraulic Machinery and Systems.2006.
[4]郑小波,罗兴琦,邬海军,等.轴流式叶片的流固耦合振动特性分析[J].西安理工大学学报,2005,21(4):342-346.
[5]张学荣.叶片在水体下的模态分析[J].排灌机械工程学报,2002,20(5):10-12.
[6]B.J.Lazan,Damping of Materials and Members in Structural Mechanics,Pergamon Press,New York,1968.
[7]Rao J S,Saldanha A.Turbomachine blade damping[J].Journal of Sound and Vibration,2003,262(3):731-738.
[8]李鹏飞.应力相关阻尼模型及其在梁式桥动力分析中的应用[D].北京交通大学,2014.
[9]吴俊男.离心压缩机半开式叶轮阻尼及动应力计算研究[D].大连理工大学,2015.
[10]Fortes-Patella R,Longatte,Kueny L.Numerical analysis of unsteady flow in a centrifugal pump[J].ASME Fluid Machinery,1995(222):41-46.
[11]Gonzalez J,Fernandez J.Blanco,E.Numerical simulation of the dynamic effects due to impeller-volute interaction in a centrifugal pump[J]-Journal of Fluids Engineering,2002,124(2):348-355.
[12]Chiang H W D,Kielb R E.An analysis system for blade forced response[J].Journal of Turbomachinery,1993,115(4):762-770.
[13]Zhifeng Yao,Fujun Wang.Experimental Investigation of Time-Frequency Characteristics of Pressure Fluctuations in a Double-Suction Centrifugal Pump[J].ASME J.Fluids Eng.,2011.10,Vol.133/101303-1.
[14]H.Tanaka.Vibration behaviour and dynamic stress of runners of very high head reversible pump-turbines,in:Proceedings of the 15th IAHR Symposium,Belgrade,1990.
[15]Rao J S,Peraiah K C,Uday K S.Estimation of Dynamic Stresses in Last Stage Steam Turbine Blades under Reverse Flow Conditions[J].Advances in Vibration Engineering,Journal of Vibration Institute of India,2009,8(1):71.
[16]Shengli Xu,Xi He,Tao Sun,Xiaofang Wang.Research of Damping and Dynamic Stress for Impeller of Reactor Coolant Pump,in:17th International Symposium on Transport Phenomena and Dynamics of Rotating Machinery,Maui,Hawaii,2017.

