一种基于不等间隔滤波器的窄带干扰抑制方法

郑相全，张先禄，杨婷婷，吴玉成

(1.军事科学院系统工程研究院，北京 100141；2.信息管理中心，北京100034；3.重庆大学 通信工程学院，重庆 400044)

0 引言

在直接序列扩频通信(Direct Sequence Spread Spectrum，DSSS)系统中，工业干扰、临近电台信号辐射和人为干扰等情况普遍存在，在扩频通信频段内形成窄带干扰(Narrow-band Interference，NBI)。虽然DSSS系统具备一定的抗干扰能力，但强干扰背景下系统性能将急剧下降。研究超过扩频增益的窄带干扰抑制技术[1-2]是DSSS系统应用中的重要话题。

常用扩频系统窄带自适应干扰抑制技术有变换域和时域2种。其中变换域方法[3-4]通常采用频域方法，通过快速傅里叶变换(Fast Fourier Transformation，FFT)处理获得接收信号中的窄带干扰信息，通过特定算法在频域消除干扰。但频域消除窄带干扰的缺陷是计算复杂度高、存储空间和计算延时较大，不能跟踪频率快速变化的窄带干扰[5]，同时对接收信号进行时域加窗处理会带来频谱泄漏等不良影响[6-7]，致使干扰无法完全消除。且在没有窄带干扰的情况下，引入频域处理会带来较大固有损耗。

时域方法[8-9]利用扩频信号和窄带干扰可预测性(即相关性)差异，估计出干扰信号，再从接收信号中减去预测的干扰信号，达到抑制干扰的目的。现有时域消除窄带干扰方法的信号预测采用自适应滤波算法[10-11]来实现，通常采用最小均方误差(Least-Mean-Square，LMS)算法或递归最小均方误差(Reiterative Least-Squares，RLS)算法及其改进算法。其中基于LMS算法[12-13]的窄带干扰抑制方案便于数字化实现，缺点是迭代次数较多，基于RLS算法窄带干扰抑制方案收敛较快，但计算较复杂。

时域窄带干扰抑制方案通常采用等间隔横向滤波器，但抑制能力有限，为了进一步提高对不同窄带干扰的抑制能力，本文提出变抽头间隔的实现方案。由于变抽头间隔方案实现复杂，所以设计能够适应多种干扰模式且阶数较低的滤波器用于窄带干扰抑制，是变抽头间隔方案工程实现中亟待解决的重要问题。本文结合实际应用，设计了一种易于FPGA实现、固有损耗低的时域自适应窄带干扰抑制方法，并通过软件仿真和实际硬件测试验证了其可行性。

1 时域窄带干扰抑制原理

扩频系统的宽带频谱内，扩频信号与窄带干扰具有不同自相关特性[14-15]。宽带扩频信号的自相关特性相当于高斯白噪声，而窄带干扰信号自相关性较强，可以被预测。基于自适应滤波原理[16]，可从接收到的当前信号预测出下一时刻窄带干扰信号，再用后一时刻接收信号减去当前时刻干扰预测值，实现窄带干扰抑制。时域窄带干扰抑制原理如图1所示。

图1 时域窄带干扰抑制原理

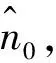
2 不等抽头间隔时域窄带干扰抑制

通常时域抗窄带干扰的横向滤波器抽头间隔为码片周期的整数倍或者小数倍[17-18]，在实际工程中，一般取数据采样周期的整数倍。

设2N+1阶横向滤波器的输入为x(t)，输出为y(t)，第i个抽头的系数为ci，延迟间隔为τi=k·TS，i=1，2，…，2N+1，TS为采样周期，k为延迟的采样时钟数。则

(1)

从频域特性的角度进行分析，若τi为某一固定值τD，即抽头间隔相同，则

(2)

由式(2)可以看出，抽头延迟间隔所产生的傅里叶变换项e-jωτD不对最终频谱成型起决定作用，滤波器频率响应仅依赖于抽头系数和输入信号，涵盖的频率特性比较单一。因此，等抽头间隔滤波器的滤波效果需要足够的阶数支撑，即抽头延迟个数很大。理论上，一个抽头数无限的等间隔预测滤波器，可消除所有窄带干扰影响，但实际工程中的抽头数量总会受到限制。另外，在工程实现时，由于等抽头间隔滤波器采样位置不变，从而导致时域信息存在着不完整性。

为此，本文提出将τi设定为变化值，则式(2)变为：

(3)

由式(3)可以看出，τi为变化值时，滤波器的频率响应不但受抽头系数和输入信号影响，而且还与抽头间隔值有关；傅里叶变换项是对多个频率特性的综合，包含的频率特性更全面，即不等抽头间隔滤波器较等抽头间隔滤波器的频谱特性更适于窄带干扰预测与抑制。另外，由于不等抽头间隔滤波器使延迟取样点更为分散，所包含的时域信息更全面，因而达到同样的窄带干扰抑制能力时，不等抽头间隔滤波器所需阶数远小于等抽头间隔滤波器所需的阶数。

对于不等抽头间隔滤波器，抽头间隔和阶数设计是关键技术之一。根据相关定理，抽头间隔按照递增素数的规律设计，其窄带干扰抑制效果易达到最佳。另外，鉴于LMS算法简单、运算量小、收敛性能稳定和易于FPGA实现，本文选取LMS算法作为变抽头间隔滤波器自适应算法。

基于上述思想，结合仿真技术，本文基于DSSS系统设计了一种不等抽头间隔的横向滤波，如图2所示。各抽头采样间隔依次为1和递增素数(2，3，5，7，11，13等)，滤波器阶数选为7阶，自适应算法为LMS。

经计算与实现，图2所示的设计方案总计需要14个乘法运算和8个加法运算，不仅运算量小，而且复杂度低。

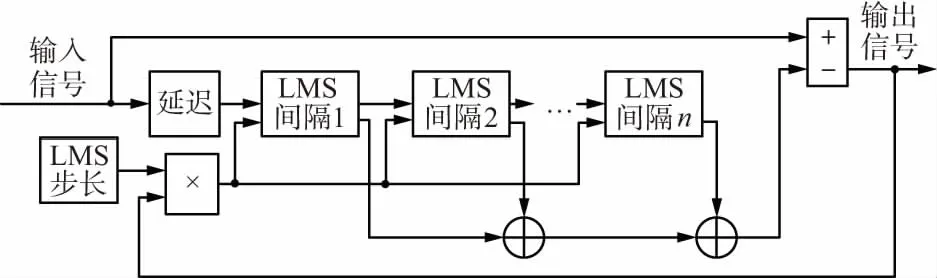
图2 不等间隔DSSS系统时域窄带干扰抑制原理

3 性能仿真

采用本文设计方法，对其抗窄带干扰能力进行验证。DSSS系统为128倍扩频，调制方式为差分格雷映射QPSK、射频带宽10 MHz。干扰类型有单频干扰、双音干扰、调相QPSK单窄带干扰以及多窄带干扰4种情况，其中多窄带干扰包含调相QPSK窄带干扰和调频CPFSK窄带干扰。仿真中未考虑信道编译码。

针对采用等间隔抽头和不等间隔预测滤波器2种情况，对DSSS通信系统误码率进行对比，结果如图3～图6所示。图3的单音干扰可位于扩频信号带宽内任意位置，信干比设置为-48 dB。图4的双音干扰分开的2个单音干扰，一个信干比为-32 dB，一个为-35 dB，总信干比为-37 dB。图5的调相干扰采用QPSK已调信号，其带宽为扩频信号的10%，信号比为-36 dB。图6的多窄带干扰包括：一个调相干扰，带宽占总带宽5%，信干比为-24 dB；2个调频干扰，带宽都为总带宽5%，信干比均为-25 dB；多个窄带干扰不重叠，总信干比-29 dB。

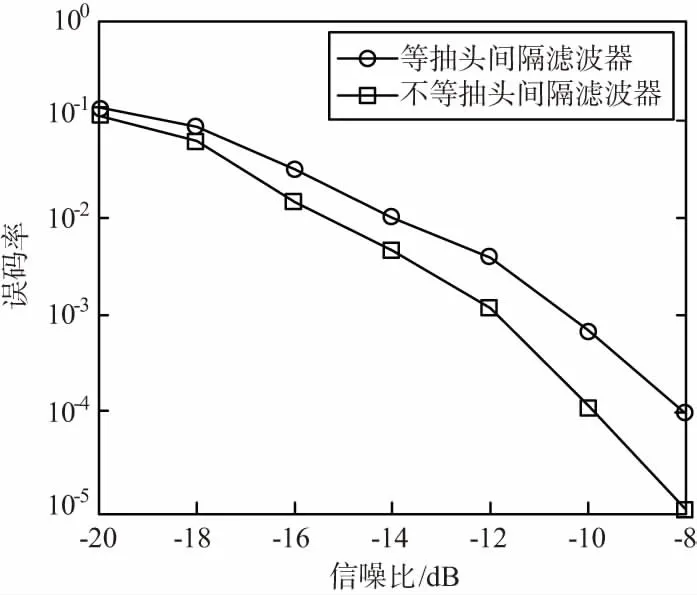
图3 单频干扰抑制后系统误码性能

图4 双音干扰抑制后系统误码性能

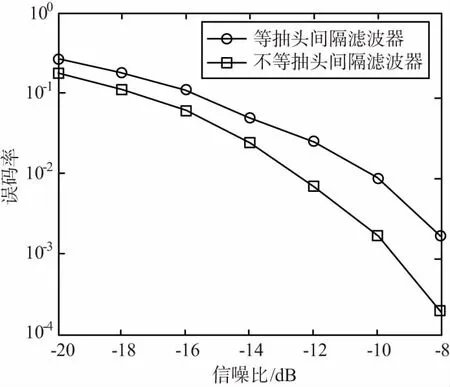
图5 调相干扰抑制后系统误码性能

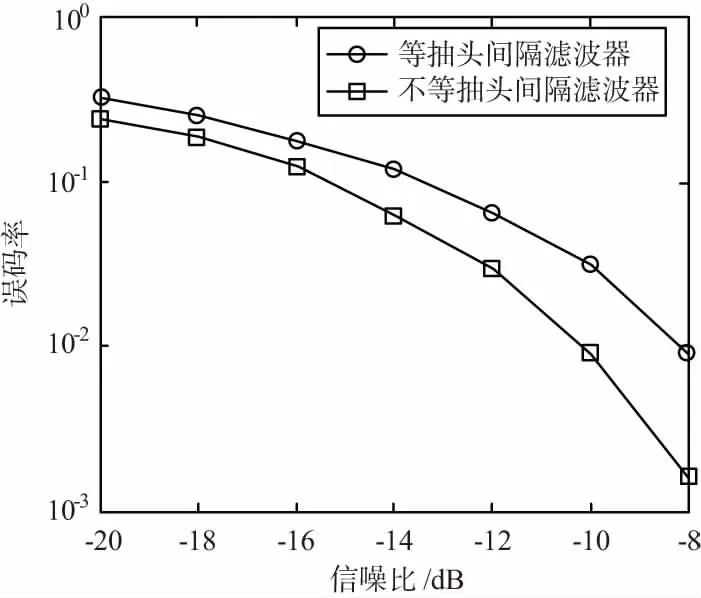
图6 多窄带干扰抑制后系统误码性能

由图3～图6可知，无论系统面临何种干扰，不等抽头间隔结构对系统性能的改善都优于等抽头间隔结构。由图3可见，当干扰为最常见的单频干扰时，可对抗的信干比达到-48 dB，扣除扩频增益21 dB，可额外获得27 dB抗窄带干扰能力。由图6可见，多窄带干扰时，本方案抗干扰能力降低，这是因为多窄带干扰信号的统计特性时域预测较困难，此时，相对频域处理，时域预测不占优势。

4 实测验证

基于本文方案，在FPGA上实现了窄带干扰抑制模块，DSSS系统参数与仿真部分一致，AD变换器位数为12位，LMS内部运算采用24位数据。在Stratix III EP3SE50芯片上，本模块共使用28个DSP单元(每个乘法运算占用2个DSP单元)，1 490个逻辑单元，241 744个存储单元，总体资源占用很少。

在保证系统正常工作前提下，对系统抗窄带干扰能力进行实测，结果如表1所示。单频干扰频率为DSSS通信系统射频带内任意频点，调相窄带干扰带宽占信号总扩频带宽的10%，中心频率为系统中心频率。

表1 抗干扰性能测试结果 (dB)

下面对抗窄带干扰性能极限进行分析。DSSS系统通常只需保证3～4 bit有效数据即可实现正常通信，再扣取1 bit符号位，采用12位AD采样时，可有7～8 bit数据用于对抗干扰，总体信干比可达-42～-48 dB。128倍扩频系统12 bit采样时，最大抗窄带干扰能力提升为27 dB。综上，提高抗干扰能力可从以下方面着手：一是增加AD采样位数，二是优化电路板设计，最大限度地降低PCB板的底部噪声。射频端未加入窄带干扰时，针对抗窄带干扰模块给DSSS通信系统带来的损耗进行测试。结果显示，对接收灵敏度影响小于1 dB。

5 结束语

DSSS系统中存在超过扩频增益的窄带干扰时，将导致系统无法工作。实际应用中，要求抗窄带干扰技术能快速适应复杂干扰模式、实现复杂度较低，且固有损耗小。基于不等抽头间隔滤波器的时域窄带干扰抑制方法，利用经不同延迟的多个抽头输出，实现对复杂模式干扰的快速估计，且所需阶数较少。后续可利用非线性自适应算法进一步提升估计收敛速度和估计精度。

[1] 郭黎利，殷复莲，卢满宏.DSSS/CDMA系统窄带干扰抑制技术概述[J].电子学报，2009，37(10)：2248-2257.

[2] 王桁，吕智勇，杨龙.DSSS卫星通信中基于小波包变换的干扰抑制方法[J].系统工程与电子技术，2016，38(6)：1417-1422.

[3] 陈彦冠，丁文锐，刘春辉.一种新的变步长频域块LMS算法[J].计算机工程与应用，2017，53(4)：140-144.

[4] 赵大恒，李春祎，孟景涛.一种频域抗干扰技术在扩频通信中的应用[J].无线电通信技术，2016，42(5)：92-95.

[5] HAO Z，ZHAO H，SHAO S，et al.Suppression of Time-varying Multi-tone Interference Based on Frequency Domain Interference Detection[J].An International Journal of Wireless Personal Communications，2014，75(2)：1051-1060.

[6] LIU F，ZHAO H，TANG YA.Variable Window Code-Aided Algorithm for Interference Suppression in DSSS Systems[J].Wireless Personal Communications，2016，88(2)：133-150.

[7] 孟东，缪玲娟，张希.反加窗算法及其在扩频系统窄带干扰抑制中的应用[J].电子与信息学报，2015，37(10)：2349-2355.

[8] HANH C，AN J P，LIU Y Q，et al.A New DSSS System Integrated Anti-jamming Algorithm[J].Transactions of Beijing Institute of Technology，2012，32(8)：844-848.

[9] 徐湛，苏中.基于时域干扰消除和能量RAKE接收的超宽带窄带干扰抑制算法[J].科学技术与工程，2013，13(15)：4181-4185.

[10] 刘泳庆，邵晓田，李一品，等.基于内插型双边带滤波器的时域自适应滤波[J].北京理工大学学报，2016，36(10)：1085-1088.

[11] 刘尚峰，王永民，郭建新，等.DSSS时变窄带干扰抑制算法研究[J].现代防御技术，2012，40(3)：99-103.

[12] 王元钦，陈源，袁嗣杰.基于变步长LMS算法的多址干扰消除研究[J].无线电工程，2011，41(2)：21-24.

[13] 张兆林，李路，姚如贵，等.基于LMS算法的窄带干扰检测技术[J].西北工业大学学报，2016，34(1)：92-97.

[14] 汪勃，谌明，梁光明，等.自适应三门限窄带干扰抑制算法[J].电子学报，2015，43(1)：13-17.

[15] 薛敦伟，周旭平.扩频通信系统中自适应陷波滤波器的性能仿真研究[J].宇航学报，2012，33(4)：500-506.

[16] 蔺晓龙，何文涛，徐建华，等.卫星导航接收机中窄带干扰抑制算法[J].计算机仿真，2014，31(1)：72-75.

[17] RAGHAVAN S A，WOLF J K，MILSTEIN L B，et al.Non-uniformly Spaced Tapped-Delay-Line Equalizers[J].IEEE Transactions on Communications，1993，41(9)：1290-1295.

[18] 王振华，范广伟，邓江娜.基于IIR开环滤波的导航接收窄带滤波器设计[J].无线电工程，2017，47(7)：78-81.