梁格法在T型梁桥静载试验中的应用研究

侯 攀，彭放枚

(1.广西交通工程检测有限公司，广西 南宁 530011；2.广西建设职业技术学院，广西 南宁 530003)

0 引言

在我国现役桥梁中，混凝土T梁桥由于构造简单、受力明确、预制施工方便等优点，成为了使用最多的桥型之一。据统计，在广西有70%的公路桥梁采用了装配式T梁桥。目前，我国的桥梁建设日趋平缓，已逐步进入桥梁养护期。为检测运营期桥梁的承载能力，桥梁荷载试验是最直接有效的方法。荷载试验最重要的一个环节是对在役桥梁的实际状况进行理论计算，对于混凝土T梁桥，目前常用的理论计算方法是单梁和梁格法计算。本文以实际工程项目为依托，验证梁格法在T梁桥荷载试验中的使用效果，并与单梁法进行比较，为梁格法在T梁桥荷载试验中的应用提供参考，同时为规范混凝土T梁桥的养护工作提供科学依据。

1 荷载试验理论计算方法原理

1.1 单梁法基本原理

单梁法是将空间结构通过横向分布理论转化为平面杆系来进行计算分析。由于T梁横向主要采用湿接缝连接，采用单梁计算时，主梁的荷载横向分布系数通常采用的是刚接法，该方法实际上是考虑了横向弯矩的完全有效传递[1]。单梁法计算快捷，建模简单，但在实际工程中，由于施工因素、荷载疲劳、病害等因素，T梁横向连接的弯矩传递效率是无法达到理想状态的，因此在后期的荷载试验承载能力评估过程中，实测值与理论值存在较大的差异。

1.2 梁格法基本原理

梁格法是用等效梁格代替桥梁上部结构，各区域内的弯曲刚度和抗扭刚度集中于邻近的等效梁格内，实际结构的纵向刚度集中于纵向梁格构件内，横向刚度则集中于横向梁格构件内。梁格等效原则理论上应满足：当原型实际结构和对应的等效梁格承受相同荷载时，两者的挠曲应恒等，任一梁格内的弯矩、剪力和扭矩应等于该梁格所代表的实际结构部分的内力[2]。采用梁格法对T梁进行分析时，由于横向连接采用了梁格构件等效，因此，可以根据实际检测状况调整横向连接构件的刚度，使理论计算更加符合实际状况。

T梁由于其结构受力明确，划分网格时应遵循如下要点[3]：

(1)对于非密排的T梁，可取单个T梁为一个纵向梁格。在进行网格划分前，应先对T梁的有效宽度进行计算，纵梁的翼缘板尺寸应不大于规范规定的有效宽度，翼缘板的有效宽度的计算按照行业标准《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62-2004)4.2.2条计算。

(2)在未设置横隔板的位置，横桥向采用翼缘板连接，主梁的纵桥向弯矩完全由T形截面承担。

(3)梁格的节段划分应符合上部结构的实际受力性能。在设置了横隔板的位置，应将横隔板单独进行梁格划分，且网格不宜过大。未设置横隔板的位置，横向梁格的大小参考纵向梁格的大小划分。

(4)内力突变区应加密网格，比如支点附近，纵、横向构件的间距应大约相等。此外静载试验关键截面附近网格加密可让理论值更加精确。

(5)结构容重的计算计入纵梁，横梁采用虚拟梁的形式，容重为0。

2 梁格法在桥梁荷载试验中的应用分析

2.1 工程概况

本文以某高速公路四跨预应力混凝土连续T形梁桥的桥梁静载试验为例进行分析。该桥桥梁跨径组合为4×40 m先简支后连续T梁。桥面总宽12.75 m，横向布置为0.5 m(防撞墙)+11.75 m(车行道)+0.5 m(防撞墙)。每跨横向布置6片T梁，梁高250 cm，边梁宽185 cm，中梁宽170 cm，湿接缝宽45 cm。设计荷载等级为：公路一级。本文取第二跨最大正弯矩的正载工况为例进行计算。T梁截面尺寸如图1～2所示。

图1 中梁跨中截面尺寸图(单位：cm)

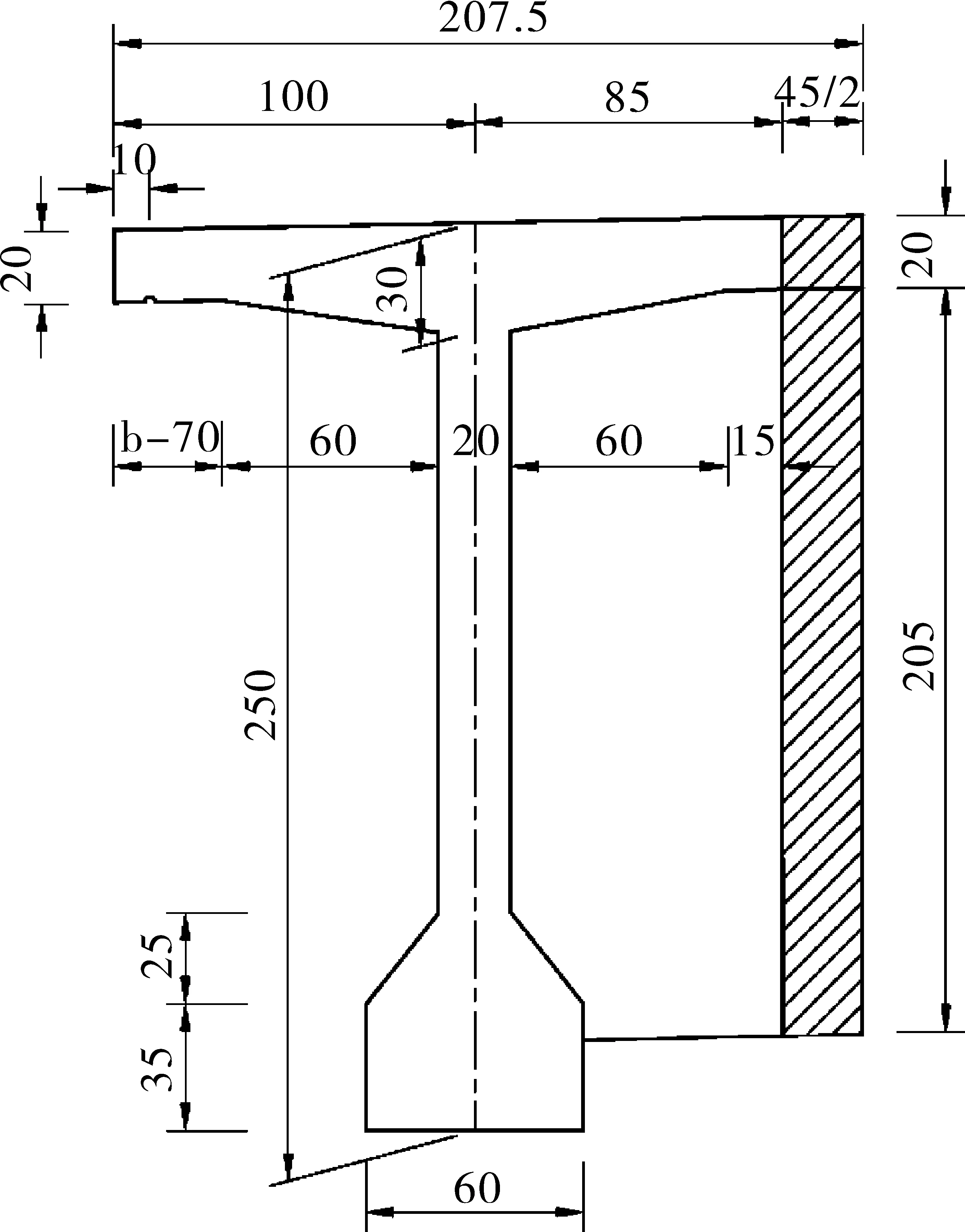
图2 边梁跨中截面尺寸图(单位：cm)

2.2 梁格法计算模型及结果分析

2.2.1 建立梁格法有限元模型

根据梁格法划分梁格的相关要求及原则，对该桥主梁纵梁翼缘板进行有效宽度计算，确定纵横向梁格尺寸和间距。网格划分如下：纵向梁格控制在1～2 m内，荷载试验关键截面处加密网格，将纵梁湿接缝1/2计入纵梁进行计算，虚拟横梁用“一”字型截面模拟，间距取1～2 m，网格划分与纵梁梁格一致，试验关键截面处网格加密，截面尺寸与湿接缝实际尺寸一致。

有限元模型的建立采用目前较常用的大型通用有限元计算软件Midas civil，结构离散图如图3～4所示。全桥共计731个节点，划分梁单元922个，为方便模拟车辆荷载的加载，另建立360个薄板单元模拟桥面板。纵梁混凝土弹性模量取3.45×104MPa，容重26 kN/m3。设计15 cm混凝土铺装，考虑到桥面铺装层混凝土施工质量、尺寸偏差等因素，计入12 cm厚混凝土铺装对上构抗弯刚度的影响。横梁及横隔板混凝土密度均取0，弹性模量与泊松比取实际值，即保证横向联系的刚度与实际一致，弯矩传递有效值采用100%。

图3 梁格结构离散图

图4 主梁梁格划分示意图

2.2.2 与单梁法理论计算结果对比分析

在T型梁桥的理论中，往往是将横向连接作为刚接进行设计的，然而在桥梁的实际运营中，受施工工艺、材料时变效应等因素的影响，横向连接的刚度显然无法达到设计的水平，而荷载试验则是测试结构横向分布系数最好的办法，通过试验结果对结构进行设计理论验证。本文分别采用刚接法和梁格法求解三车道汽车荷载作用下跨中截面的横向分布系数，计算结果见表1，从表中可见，用刚接法计算横向分布系数与梁格法计算的横向分布系数绝对差值在0.01以内，计算结果比较吻合。在实际的运营过程中，横向连接部分伴随病害的发展以及材料性能的退化，横向弯矩传递能力降低，下文将通过荷载试验的结果对其横向弯矩的传递有效值进行研究。

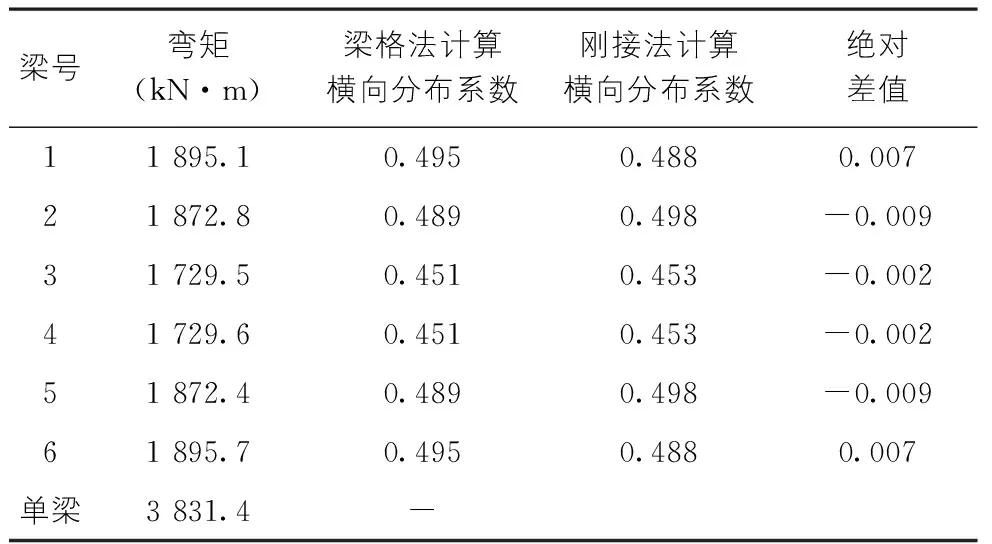
表1 荷载横向分布系数对比结果表

静载试验加载根据现行规范[4]的相关要求进行，加载采用6辆35 t三轴汽车，加载车布置如图5～6所示。加载效率控制在0.95～1.05之间，加载效率计算结果见表2，从计算结果可以看出，梁格法和单梁计算结果基本一致，单梁法计算结果略低于梁格法。

表2 静载试验加载效率表

图5 静载试验加载车辆布置示意图(单位：cm)

图6 测点布置示意图(单位：cm)

2.2.3 静载试验结果分析

在加载车辆的作用下，该桥跨中截面测试结果见表3、表4。根据各测点的实测挠度值和应变值，按照每片梁挠度(应变)与所有梁挠度(应变)总和的比值绘制实测结果的横向分配系数曲线，与理论横向分配曲线进行比较，见图7～8，由图可知本桥实测横向分配与理论计算基本相符，但从横向分配曲线可知，实测横向弯矩的有效值传递水平低于理论横向弯矩的传递。

表3 挠度测试结果分析表

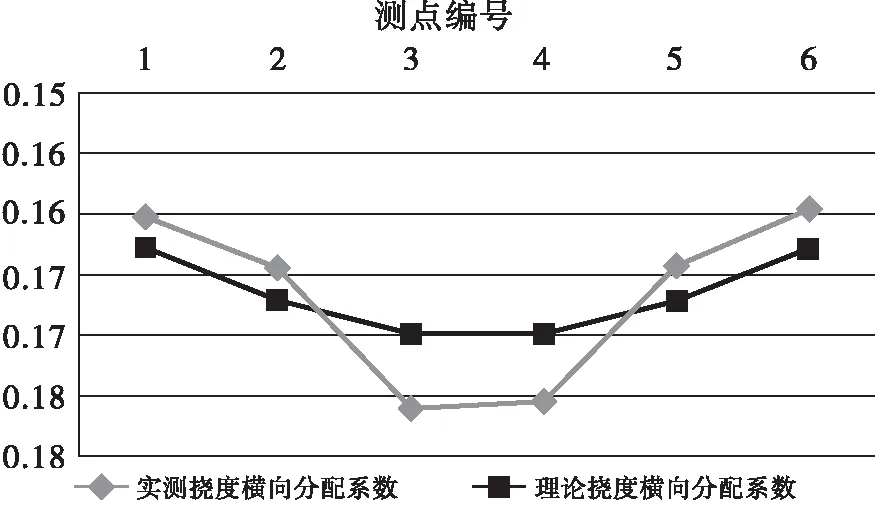
图7 测试跨满载挠度横向分配系数图

测试截面数据类型2#跨测试截面B(正载)1#2#3#4#5#6#挠度应变弹性值(με)404345464440应变理论计算值(με)747576767474校验系数0.5390.5730.5930.6060.5910.541

图8 测试跨满载应变横向分配系数图

3 结语

对于梁格法在T型预应力混凝土连续梁桥中的运用，得出如下结论：

(1)根据实际案例分析结果得出，梁格法能够较好地模拟空间结构的受力状况，不需要通过传统手段计算桥梁的横向分布系数以及偏载系数，计算简单明确，数据精度满足T型连续梁桥进行荷载试验的要求。

(2)与单梁模型理论计算结果基本一致，弯矩计算结果略高于单梁法，弯矩的计算过程较单梁法具有较高的简便性。

(3)根据实测横向分配系数与理论横向分配系数对比可知，结构在运营过程中的实际横向分配系数低于理论的横向分配系数，而梁格法可以通过调整横向连接的刚度系数调整横向弯矩的横向传递效率，更加准确地模拟结构的实际受力状况，具有更高的适用性。

[1]邵旭东.桥梁工程[M].北京：人民交通出版社，2016.

[2]戴公连.桥梁结构空间分析设计方法与应用[M].北京：人民交通出版社，2001.

[3]李国豪.公路桥梁荷载横向分布计算[M].北京：人民交通出版社，1984.

[4]JTG/T J21-01-2015，公路桥梁荷载试验规程[S].