偏心轮式步进梁升降过程力学数学模型

俞洪杰，张康武，郭 韡，赵流韵，吕阳阳

(中国重型机械研究院股份公司，陕西 西安 710032)

0 前言

步进梁是钢卷包装生产线上的核心设备，用于运输钢卷。偏心轮式步进梁结构简单、刚性好、停位准确，维护方便，故障率低。在偏心轮式步进梁设计中，偏心轮式机构设计较复杂，偏心轮的受力分析繁琐。文献[1]采用了作图法计算升降油缸的受力，本文运用解析法分别求解拉缸式步进梁和推缸式步进梁升降油缸的受力。

1 偏心轮式步进梁的结构及工作原理

步进梁由活动梁、固定梁、连杆、偏心轮、升降油缸、横移油缸等组成，如图1所示。活动梁和固定梁上均有若干个相同步距的鞍座。活动梁是通过上升、横移、下降和回退四种动作，在每一个运行周期内把所有钢卷从一个固定鞍座向前移动一个步距到下一个固定鞍座。

偏心轮式步进梁的升降主要利用偏心距得以实现，偏心轮安装在活动梁上，偏心轮与活动梁之间有轴承连接，活动梁的车轮安装在偏心轮的偏心位置，车轮中心与偏心轮中心距离就是偏心距，油缸的伸缩带动偏心轮转动，由于车轮始终与安装在固定梁上的轨道接触，车轮中心的标高不会变，所以偏心轮中心的高度会因其转动而变化，活动梁也就随之升降[1,2]。

图1所示的步进梁为拉缸式步进梁，即升降油缸活塞杆全部伸出时，活动梁在最低位，活塞杆拉回，活动梁逐渐升高。推缸式步进梁的工作原理是，升降油缸活塞杆全部缩回时，活动梁在最低位，活塞杆推出，活动梁逐渐升高。

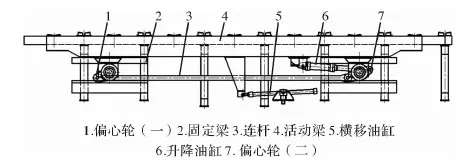
图1 偏心轮式步进梁结构

2 拉缸式步进梁机构受力分析

2.1 步进梁运动机构简化

以中国重型机械研究院股份公司为鞍山某钢厂设计的偏心轮式步进梁为研究对象，此步进梁的升降油缸的工作方式是拉缸，即油缸缩回，活动梁上升。将步进梁的运动机构进行简化，如图2所示。C点对应油缸铰接中心，A点对应车轮中心，D点对应偏心轮中心。

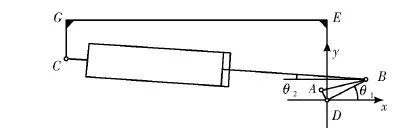
图2 机构简图(拉缸)

2.2 建立矢量方程

因该机构在实际运动时，没有静止的固定点，故只能选取动点作为原点建立矢量方程。因与活动梁固联的C、D、E、G各点均随活动梁做竖直方向直线运动，故将D点选为原点，由DB杆和BC杆的关系建立矢量方程。

(1)

将式(1)改写为分量形式

(2)

2.3 解活动梁上升距离

由方程组(2)，消去θ2

2·lBD·(lDE-lCG)·sinθ1-2·lBD·lEG·cosθ1+[(lBC-l)2-lBD2-lEG2-(lDE-lCG)2]=0

(3)

同理，消去θ1，得

(4)

符合公式：A·sinθ+B·cosθ+C=0

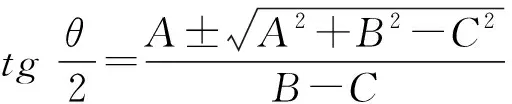
(5)

根据式(5)可计算θ1和θ2。

以油缸未缩回时机构的位置为原始位置。因∠ADB为直角，故∠ADE=∠θ1。故D点上升的位移，即活动梁上升距离

S=lAD·cosθ10-lAD·cosθ1

(6)

其中θ10为原始位置的θ1。

根据计算数据作出活动梁上升距离随油缸缩回距离的变化规律图，如图3所示。可见随着油缸的缩回，活动梁逐渐上升，基本呈线性关系。

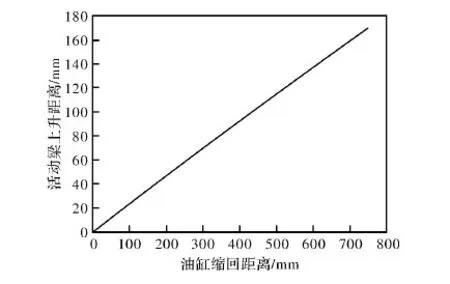
图3 活动梁上升距离随油缸缩回距离的变化规律图

2.4 机构受力分析

由活动梁受力分析知A点受地面竖直向上的支撑力大小等于活动梁载荷。A点受力分析如图4所示。

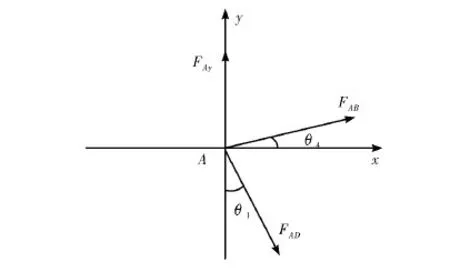
图4 A点受力分析图

由A点受力平衡

(7)

解得

(8)

作B点受力分析图，如图5所示。

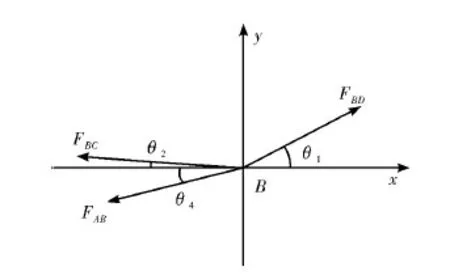
图5 B点受力分析图

由B点受力平衡

(9)

解得

(10)

FBC即油缸所需的拉力。

3 拉推缸式步进梁机构受力分析

3.1 步进梁运动机构简化

以中国重型机械研究院股份公司为柳州某钢厂设计的偏心轮式步进梁为研究对象，此步进梁的升降油缸的工作方式是推缸，即油缸伸出，活动梁上升。将步进梁的运动机构进行简化，如图6所示。

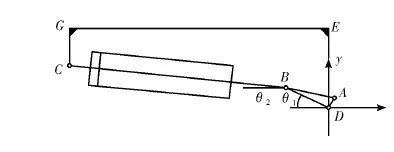
图6 机构简图(推缸)

3.2 建立矢量方程

同样，将D点选为原点，由DB杆和BC杆的关系建立矢量方程。

(11)

将式(11)改写为分量形式

(12)

3.3 求解活动梁上升距离

由方程组(12)，消去θ2，得

(13)

同理，消去θ1，得

(14)

根据式(5)可计算θ1和θ2。

以油缸未伸出时机构的位置为原始位置。因∠ADB为直角，故∠ADE=∠θ1。故D点上升的位移，即活动梁上升距离

S=lAD·cosθ10-lAD·cosθ1

(15)

其中θ10为原始位置的θ1。

根据计算数据作出活动梁上升距离随油缸伸出距离的变化规律图，如图7所示。可见随着油缸的伸出，活动梁逐渐上升，基本呈线性关系。

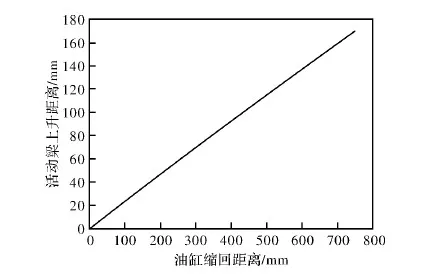
图7 活动梁上升距离随油缸伸出距离的变化规律图

3.4 机构受力分析

由活动梁受力分析知A点受地面竖直向上的支撑力大小等于活动梁载荷。A点受力分析如图8所示。

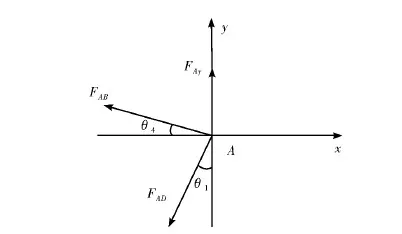
图8 A点受力分析图

由A点受力平衡

(16)

解得

(17)

B点受力分析，如图9所示。

图9 B点受力分析图

由B点受力平衡

(18)

解得

(19)

FBC即油缸所需的推力。

4 工程算例

4.1 拉缸式步进梁算例

根据所研究的拉缸式步进梁的结构及工况可知，当活动梁上升距离小于100 mm时，活动梁未能接触到钢卷，其载荷即自重，即FAy=20 t；此步进梁最大载荷为120 t，当上升距离大于100 mm时，活动梁的载荷FAy=140 t。

根据公式(3)～(10)，编制了计算程序，作出油缸的拉力随油缸缩回距离的变化规律图，如图10所示。由图可知，随着油缸的缩回，活动梁的上升，油缸拉力的总体趋势是逐渐增大；当油缸还差30 mm未缩回时，油缸拉力的增幅较大；当油缸完全缩回，活动梁上升到最高点，油缸的拉力达到极大值。

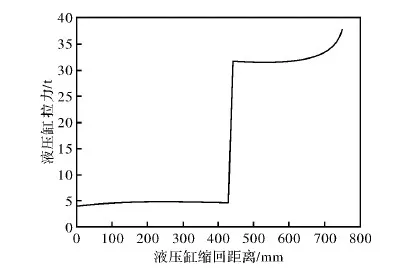
图10 油缸的拉力随油缸缩回距离的变化规律图

4.2 推缸式步进梁算例

此推缸式步进梁和上面研究的推缸式步进梁的工况和载荷相同。

根据公式(13)～(19)，编制了计算程序，作出油缸的推力随油缸伸出距离的变化规律图，如图11所示。由图可知，当油缸伸出440 mm时，此时即活动梁刚接触钢卷，油缸所需推力急剧增大，达到极大值，随后逐渐减小。

图11 油缸的推力随油缸伸出距离的变化规律图

5 结论

本文对两种类型(拉缸式和推缸式)偏心轮式步进梁机构在升降过程中进行了受力分析，建立了活动梁上升距离、油缸受力的数学模型，根据计算数据作出了油缸受力在活动梁整个上升过程中的变化规律图。可直观得看出拉缸式步进梁升到最高位置，油缸受力最大，推缸式步进梁在活动梁刚接触钢卷时，油缸受力最大。这个规律对此类型偏心轮式步进梁均适用。根据计算极大值和系统的工作油压，选择合理的升降油缸，这两种类型步进梁已投入使用多年，运行情况良好。

[1] 张令琴.偏心轮式步进梁的机构设计及计算[J].重型机械，2009(06)：50-52.

[2] 梁芳，赵宗刚.步进梁运输机特点及工作原理[J].科学时代，2013(12).

[3] 高荣元.钢卷运输机械[M].北京：冶金工业出版社，1984.

[4] 张红亮，张红丽，王娜.钢卷运输线步进梁调试与改造[J].电气应用，2009(04)：68-70.

[5] 杨韶光，杨帆.偏心轮杆式升降步进梁运动分析和推力计算[J].固体力学学报，2008(12)：216-219.

[6] 杨国良，康健. 偏心轮式升降步进梁升降运动分析[J].冶金设备，2014(04)：35-37.

[7] 黄庆学.轧钢机械设计[M].北京：冶金工业出版社，2007.

[8] 哈尔滨工业大学理论力学教研室.理论力学[M].北京：高等教育出版社，2002.

[9] 西北工业大学机械原理及机械零件教研室.机械原理[M].北京：高等教育出版社，2006.

[10] 成大先.机械设计手册[M].北京：化学工业出版社，2007.

[11] 许波，刘征.MatLab工程数学应用[M].北京：清华大学出版社，2000.